Миронов С.В., Пищухин А.М. Метасистемный подход в управлении
Подождите немного. Документ загружается.

61
4 Оптимизация управления в метасистемах
4.1 Обсуждение критериев оптимального управления
Назначение минимизируемого критерия оптимизации режима системы
является, как известно, самой важной задачей оптимизации. Она не может
целиком решаться формализованными методами.
Для детерминированных процессов с непрерывным временем в качестве
критерия оптимальности процесса управления обычно принимают классиче-
ский функционал /27/ I(t
0
, Y, u, t
к
), где t
0
– начальный, t
к
– конечный момент
времени управления
t
к
I(t
0
, Y, u, t
к
) = ℓ(Y, t
к
) + ∫ (L(Y, τ) + u
т
(τ)K
-1
u(τ))dτ . (4.1)
t
0
Функционал такого типа содержит первое слагаемое, оценивающее точ-
ность приведения управляемого процесса в желаемое конечное состояние
Y(t
к
). Эта часть функционала часто называется терминальной. Второе сла-
гаемое является интегральной оценкой качества переходного процесса,
третье слагаемое характеризует потери на управление. Здесь
K – матрица па-
раметров, отражающая степень влияния управляющего воздействия на инте-
гральную часть этого критерия.
Применительно к метасистемам последовательного действия критерий
должен отбирать системы с максимальным быстродействием и максимально
адекватным включением нужной структуры (другие два показателя качества
– устойчивость и нечувствительность к внутренним изменениям можно счи-
тать удовлетворительными в рамках рассмотренной выше конечноавтомат-
ной модели). В таких случаях подынтегральную часть берут постоянной, а
терминальную (поскольку речь идет о включении структур) необходимо вы-
разить через вероятности включения различных структур. Таким образом,
классический критерий требует в данном случае некоторого преобразования.
В нашем случае в качестве функций ℓ1 примем сумму разностей вероят-
ностей переходов внешнего и внутреннего процессов из одного стояния в
другое
∑
=
−=
N
l
l
.внутр
l
.внешнk
)PP()t,Y(
1
1
l
, (4.2)
а L(Y,
τ), исходя из требований быстродействия, приравняем 1.
При перераспределении управляющих ресурсов в метасистеме парал-
лельного действия критерий (4.1) можно использовать непосредственно, если
ресурсы в разных структурах одинаковы по природе или могут быть сведены
к одинаковым единицам измерения. В этом случае компоненты вектора
управляемых величин и компоненты управляющих воздействий будут соот-
ветствовать разным структурам и критерий «автоматически» оптимально пе-
рераспределит управляющие воздействия.
62
Такого невозможно добиться с помощью данного критерия в отношении
точности поддержания заданных значений управляемых величин. В этом
случае необходимо, чтобы критерий оптимального управления включал дис-
персии выходных величин и управляющие воздействия, направляемые на
поддержание этих дисперсий на заданном уровне.
Считая данный функционал отражающим потери в метасистеме, при-
мем, что
)t,Y(l
k1
= 0, функция
L
зависит не от управляемых величин, а от их
дисперсий, а вместо обычной работы управляющих воздействий использует-
ся виртуальная (вводится ниже)
∑
∫
=
∞
+=
n
i
t
iii
dtttAtI
1
0
))),(()((
σσα
. (4.3)
Дальнейшие рассуждения по поводу требований к критерию привязаны
к более конкретным задачам, описанным ниже.
4.2 Согласование процессов случайной структуры
Как показано выше (в разделе 2.1), в системах управления, функциони-
рующих на принципе последовательно переключаемых структур, имеют ме-
сто два процесса случайной структуры: один тесно связан с изменением
внешних условий и формирует уставки для другого. Второй процесс является
исполнительным и переводит объект управления в заданное первым процес-
сом состояние. От согласованного функционирования этих двух процессов
зависят такие важные качественные показатели системы управления, как
точность и быстродействие.
Постановка задачи. Имеются два процесса случайной структуры, со-
стояние одного из которых (ведомого) определяется состоянием другого (ве-
дущего). Ведущий процесс описывается векторным стохастическим диффе-
ренциальным уравнением вида
,),...1(,)(),(),(),()(
00
)()()(
sWtWttWHtWtDW ==+= l
&
lll
ζϕ
(4.4)
где
W – вектор фазовых координат процесса,
t – время,
s – число структур (различных состояний),
)(
)(
tD
l
– матрица порядка n×n детерминированных параметров с компо-
нентами d
kr
(ℓ)
(t),
ϕ
(ℓ)
(W,t) – векторная детерминированная нелинейная функция (вектор-
столбец) с компонентами ϕ
1
(ℓ)
, …, ϕ
n
(ℓ)
,
63
H
(ℓ)
(W,t) – матрица n×m или n×n с нелинейными относительно W ком-
понентами h
ij
(ℓ)
(W,t) (i = 1,…, n, j = 1,…, m),
ς(t) – вектор гауссова белого шума с компонентами ς
1
(t), …, ς
m
(t).
Вектор белого шума ς(t) будем считать случайным центрированным
процессом с корреляционной функцией
)()(),(
tttGttK
′
−
=
′
δ
ζ
(4.5)
где
G(t) – симметричная матрица интенсивностей с компонентами G
ij
(t).
Ведомый процесс является управляемым и описывается подобным урав-
нением
),...,1(,)(),(),(),(),()(
00
)()()()(
sYtYtVtYHutYtYtDY ==++= l
&
llll
σϕ
(4.6)
где σ
(ℓ)
(Y,t) – матрица детерминированных нелинейных функций σ
ij
(ℓ)
,
u – вектор управляющих воздействий,
V(t) – вектор гауссова белого шума с компонентами V
1
(t), …, V
m
(t).
Ведущий процесс измеряется с помощью канала наблюдения, в резуль-
тате чего имеется m-мерный наблюдаемый процесс
),...,1()(),,()(
)(
1
)(
stNtuWCtZ =+= l
ll
, (4.7)
где
C
(ℓ)
(W, u
1
, t) – m-мерная векторная функция,
u
1
– вектор управляющих воздействий на канал наблюдения,
N
(ℓ)
(t) – белый гауссов шум с матрицей интенсивностей Q
(ℓ)
(t), статисти-
чески не зависящий от ς
(t).
Требуется так подобрать векторы управлений
u и u
1
, чтобы процессы
были максимально согласованы по включаемой структуре и по быстродейст-
вию переключения на необходимую структуру.
Оптимизация управления ведомым процессом. Вопросы системной
согласованности рассмотрены в третьей главе. Применим рассмотренные там
положения к согласованию двух стохастических процессов в соответствии с
принятой в работе концепцией. В данном случае согласование процессов
можно провести с помощью решения задач оптимизации.
Тогда в качестве функций ℓ
1
примем разность вероятностей переходов
процессов из одного состояния в другое, учитывая при этом марковость про-
цесса, а также то, что в дальнейшем используется уравнение Колмогорова,
примем
))(|)(()(|)(((),(
1
2
11
2
1 −−
−==
hhhk
twtwtytyUtY
ωω
l , (4.8)
а L(
Y, τ), исходя из требований быстродействия, приравняем 1.
Как известно /28/, марковский случайный процесс подчиняется уравне-
нию Колмогорова (причем в данном случае первому уравнению /21/ для того,
чтобы оно было согласовано по направлению движения во времени с приме-
няемым в дальнейшем уравнением Беллмана)
64
∂ω
(ℓ)
(w, t|w
*
,t
*
) n ∂
—————— + ∑ — (A
k
(ℓ)
(w, t) ω
(ℓ)
(w, t|w
*
,t
*
)) +
∂t k=1 ∂w
k
1 n n ∂
+ — ∑ ∑ ——— (B
km
(ℓ)
(w, t) ω
(ℓ)
(w, t|w
*
,t
*
)) = 0, (4.9)
2 k=1 m=1 ∂w
k
∂w
m
где
w
k
(t + ∆t) – w
k
(t)
A
k
(ℓ)
(w, t) = lim M [———————— | w,t ], (4.10)
∆t→ 0 ∆t
(w
k
(t + ∆t) – w
k
(t)) (w
k
(t + ∆t) – w
k
(t))
B
km
(ℓ)
(w, t) == lim M [———————————————— | w,t ], (4.11)
∆t→ 0 ∆t
M[•] – символ осреднения.
Поскольку какая-нибудь структура обязательно должна реализоваться в
любой момент времени на плотности вероятности, а через них и на управ-
ляющие воздействия (через уравнение Колмогорова) наложено ограничение:
интеграл от суммы плотностей вероятности реализации всех структур дол-
жен быть равен единице.
В уравнение ведомого процесса входит неизвестная пока функция
управляющих воздействий f[σ
(ℓ)
(Y,t)]
∂ω
(ℓ)
(y, t|y
*
,t
*
) n ∂
—————— + ∑ — (A
k
(ℓ)
(y, t) ω
(ℓ)
(y, t|y
*
,t
*
)) + f [σ
(ℓ)
(Y,t)] +
∂t k=1 ∂y
k
1 n n ∂
+ — ∑ ∑ ——— (B
km
(ℓ)
(y, t) ω
(ℓ)
(y, t|y
*
,t
*
)) = 0. (4.12)
2 k=1 m=1 ∂y
k
∂y
m
Эта функция играет в уравнении роль источника возникновения и по-
глощения реализаций случайного процесса.
65
Вычитая из (4.9) (4.12), получим уравнение относительно U
∂U
(ℓ)
n ∂
—— + ∑ — (A
k
(ℓ)
(y, t) U
(ℓ)
) + f [σ
(ℓ)
(Y,t)] +
∂t k=1 ∂y
k
1 n n ∂
+ — ∑ ∑ ——— (B
km
(ℓ)
(y, t) U
(ℓ)
) = 0. (4.13)
2 k=1 m=1 ∂y
k
∂y
m
Поскольку один процесс “копирует” другой лишь с опозданием и воз-
можными ошибками, дифференцирование по w и y здесь совершенно эквива-
лентно.
Полагая далее
1 ∂U
(l)
∂U
(ℓ)
f [σ
(ℓ)
(Y,t)] = — [——]
т
σ
(ℓ)
Kσ
(ℓ)
[ ——] + M[L(Y, τ)], (4.14)
4 ∂y ∂y
получаем точно такое же уравнение как в /28, формула (8.69) на с. 283/, име-
нуемое также стохастическим принципом минимума обобщённой работы
/27/, которому должна удовлетворять функция U для того, чтобы управление
было оптимальным и равным
1 ∂U
(ℓ)
u
(ℓ)
= - — K[σ
(ℓ)
(Y
(ℓ)
, t)
т
——]. (4.15)
2 ∂y
Общий критерий оптимизации можно сложить из полученных частных
s s t
к
I(t
0
, Y, u, t
к
) = ∑ I
ℓ
(t
0
, Y, u, t
к
) = ∑[ℓ
1
(Y, t
к
) + ∫ (1 + u
т
(τ)K
-1
u(τ))dτ]. (4.16)
ℓ=1 ℓ=1 t
0
Добиваясь оптимального управления для каждой случайной структуры
ℓ, мы достигнем минимального общего критерия.
Оптимизация обратной связи в канале измерений. Будем полагать,
что управления
u
1
(t) в канале наблюдения являются функцией фазовых коор-
динат оптимального фильтра, т.е. выбираются таким образом, что не нару-
шаются условия марковости совместного процесса {
Y(t), Z(t)}
т
. При этих ус-
66
ловиях нормированные апостериорные плотности вероятности
(
)
(
)
ty,
€
1
l
ω
,
ω
1
(ℓ)
(y, t) фильтруемого процесса для каждого из состояний будут удовлетво-
рять обобщенным уравнениям Стратоновича
∧
∂ω
1
(ℓ)
(w, t) ∧ 1 ∧ ∞ ∧
———— = -divπ
(ℓ)
(w,t) - — ω
1
(ℓ)
(w, t)[f
(ℓ)
(w, z, u,t) - ∫f
(ℓ)
(w, z, u,t) ω
1
(ℓ)
(x, t)dx]+
∂t 2 -∞
s ∧ ∧
+ ∑ [v
rℓ
(w,t) – u
rℓ
(w,t)]. (4.17)
r =1
∧
Вектор плотности потока вероятности π
(ℓ)
(w,t) равен
∧ ∧ 1 n ∂ ∧
π
(ℓ)
(w,t)=A
p
(ℓ)
(w,t)ω
1
(ℓ)
(w, t) - — ∑ — [B
pq
(ℓ)
(w, t)ω
1
(ℓ)
(w, t)] (p = 1,n;ℓ = 1,s),
2 q=1∂y
q
(4.18)
где A
p
(ℓ)
,B
pq
(ℓ)
– коэффициенты сноса и диффузии, приведенные выше;
f
(ℓ)
(w, z, u,t) – производная от логарифма функции правдоподобия опре-
деляется по формуле
r Q
pq
(ℓ)
(t)
f
(ℓ)
(w, z, u,t) = ∑ ——— [z
p
(t) – C
p
(ℓ)
(w, u, t)][ z
q
(t) – C
q
(ℓ)
(w, u, t)] (4.19)
p,q=1 |
Q
(ℓ)
(t)|
и дополнительно зависит от функции управления в соответствии с уравнени-
∧ ∧
ем наблюдения (4.7); v
rℓ
(w,t), u
rℓ
(w,t) – соответственно функции поглощения
и восстановления реализаций случайного процесса.
Задача управляющей части ведущего процесса - оптимальная фильтра-
ция сигналов, поступающих от внешней среды. Такая задача решена в /28/ в
предположении квадратичной функции потерь
∧ ∧
Ψ(
w, W
0
,t) = [w – W
0
]
т
[w – W
0
], (4.20)
∧
где
W
0
– оптимальная оценка сигналов. Сама процедура нахождения опти-
мальных управлений существенно зависит от вида функций коэффициентов
статистической линеаризации и задаваемых ограничений. Если известно, что
минимизируемая функция потерь одномодальная и ограничения на управле-
ния отсутствуют, оптимальные управления могут быть найдены из системы

67
уравнений
s m Q
pq
(ℓ)
(t) n ∂ ∂
∑ ∑ ——— ∑ [ — c
pj
(ℓ)
(u,t)c
qk
(ℓ)
(u, t) + c
pj
(ℓ)
(u, t) — c
qk
(ℓ)
(u,t)]×
l=1 p,q=1 |
Q
(ℓ)
(t)| i,j,k=1 ∂u
f
∂u
f
×[R
ji
(ℓ)
(t)R
kj
(ℓ)
(t) + R
jk
(ℓ)
(t)R
ij
(ℓ)
(t)] = 0, (4.21)
где использованы обозначения
∞ ∧ ∧ ∧
R
ij
(ℓ)
(t) = ∫ (w
i
– W
i
(ℓ)
) (w
j
– W
j
(ℓ)
) ω
1
(ℓ)
(w, t)dw. (4.22)
-∞
Для согласования ведомого процесса с ведущим необходимо решать эту
задачу с заменой выходного вектора сигналов
W на Y, что обеспечит макси-
мальное быстродействие, управляя каналом наблюдения до тех пор, пока не-
обходимая структура не установится в ведомом процессе.
4.3 Экспериментальное исследование последовательной метаси-
стемы
Из проведенного в предыдущем параграфе исследования следует необ-
ходимость быстрого уравнивания вероятностей включений для всех струк-
тур, входящих в систему с соответствующей вероятностью изменений хода
внешнего процесса. Исходя из управляемости второго процесса, можно вве-
сти главную обратную связь, которая будет следить за реальной частотой
включений каждой структуры, запоминать ее и уравнивать с требуемой веро-
ятностью. Причем срабатывать эта связь должна только в случаях наиболь-
шей неопределенности, то есть как это следует из рассуждений, проведенных
в разделе 2 на границах между классами управленческих ситуаций. Экспери-
ментальное исследование и было посвящено оценке точности включений
структур, которую должна резко повысить указанная обратная связь.
Модель представляла собой две последовательно переключаемые ло-
кальные системы управления (структуры), изображенные на рисунке 4.1.
Здесь
21
, ww - уставки регуляторов по частоте включения, <w> - оценка веро-
ятности включения регуляторов.
Работа схемы без обратной связи (на рисунке не изображена) сравнива-
лась с работой схемы при ее наличии в условиях зашумленности внешнего
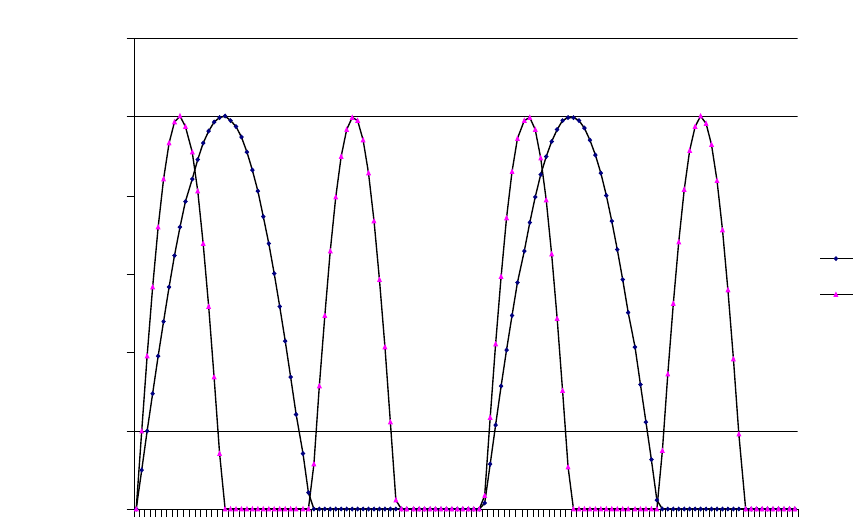
процесса. Изменения внешнего процесса без шума изображены на рисунке
4.2 и представляют собой две синусоиды с отличающимся в два раза перио-
дом.
Обратная связь срабатывает только в определенном диапазоне, когда
разность значений зашумленных синусоид меньше некоторого числа ε. Кор-
рекция в схеме с обратной связью осуществляется только за счет наращива-
ния частоты включений. Ошибки рассчитывались как отношение модуля

68
разности частоты включений в схемах с шумом с частотой включения в схе-
ме без шума к последней частоте и брались в процентах. Полученная в ре-
зультате эксперимента зависимость ошибок включений приведена на рисун
Рисунок 4.1 – Схема двух последовательно переключаемых систем ло-
кального управления
ке 4.3. Программа, реализующая описанную модель, написана на алго-
ритмическом языке Паскаль версии 7.0 и приведена в Приложении.
Как видно из графика (рисунок 4.3), некоторая ошибка у схемы с обрат-
ной связью имеет место лишь при малых ε, сравнимых с максимальным
уровнем шума. С ростом ε ошибка быстро уменьшается и обращается в нуль
для обоих включаемых систем локального управления. В то же время во вто-
рой схеме ошибки включения локальных систем управления различаются. Их
незначительная зависимость от ε обусловлена лишь шумом.
w2
w1
<w>
Объект
управления
Внешний
процесс
Регуля-
тор 1
Регуля-
тор 2
69
4.4 Координация в метасистеме
По-другому обстоит дело с метасистемой параллельного действия. Здесь
необходимы дополнительные теоретические исследования.
Постановка задачи. Пусть каждая ветвь метасистемы представляет
стохастический регулятор, описываемый уравнением Ито
() ()()
(
)
(
)
(
)
()()
=
⋅
+
=
.що,що
,t,щ dw,tt,щоG,tt,щоШt,щdо
0
0
(4.23)
От уравнения Ито однозначно можно перейти к уравнению Колмогорова
/21/ (интеграл от плотности вероятности по переменной X равен единице)
время
Рисунок 4.2 – График изменения во времени внешнего процесса
0
0,2
0,4
0,6
0,8
1
1,2
0.0
3.5
7.0
8.5
10.
sin(t)
sin(2t)
Амплит
уд
а

70
Диапазон срабатывания обр. связи (
ε)
Рисунок 4.3 – Зависимости ошибки по частоте включения локальных
систем управления в двух исследуемых схемах
∑∑∑
===
=
∂∂
∂
⋅+
∂
∂
⋅+
∂
∂
n
1k
n
1k
n
1m
mk
2
km
k
k
0
xx
f
)t,X(b
2
1
x
f
)t,X(a
t
f
. (4.24)
Специальной подстановкой /29/ из уравнения (4.24) можно убрать вто-
рое слагаемое. Управляющее воздействие попадает в правую часть и делает
это уравнение неоднородным.
Необходимо определить оптимальные управляющие воздействия для
нормального распределения вероятности.
Решение преобразованного неоднородного уравнения (4.24) можно вы-
разить через функцию Грина
()
()
()
ξξ
ξ
π
dtdt,u
bt4
y
exp
bt2
1
)y
b
a
t
b
a
exp(t,Yf
0
2
2
∫∫
∞
∞−
∞
−
−−=
. (4.25)
Подставляя в левую часть этого решения желаемый результат управления
(плотность вероятности в виде нормального закона), получаем уравнение
Фредгольма 1-го рода
()
()
()
ξξ
ξ
π
σ
πσ
dtdt,u
bt4
y
exp
bt2
1
)y
b
a
t
b
a
exp(
2
yy
exp
2
1
0
2
2
2
2
уст
∫∫
∞
∞−
∞
−
−−=
−
−
.
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
0
.001
0
.
091
0
.
181
0
.
271
0
.36
1
0.451
0
.
541
Ошибка по включениям, %
