Миронов С.В., Пищухин А.М. Метасистемный подход в управлении
Подождите немного. Документ загружается.


71
(4.26)
С помощью этого уравнения можно исследовать динамику системы
управления. Ограничимся исследованием установившегося движения. Для
этого, вернувшись к уравнению (4.24) для одномерного случая с постоянны-
ми коэффициентами
a и b, уберем производную по времени и подставим
вместо плотности вероятности нормальный закон распределения:
)y(ue)yy(
a
2
b
)yy(
2
b
2
1
2
уст
2
)yy(
уст
33
2
уст
5
=⋅
−−−−
−
−
σ
σσσ
π
, (4.27)
где
y
уст
- уставка регулятора,
u(y) - управляющее воздействие.
Введем понятие виртуальной работы как работы, которую необходимо
совершать системе управления для поддержания дисперсии выходной вели-
чины на заданном уровне
() ()
dyeyuA
ус
yy
2
2
2
2
1
у
ру
у
)( −
−
∞
∞−
∫
= . (4.28)
Пользуясь формулой (4.27), можно построить зависимость дисперсии
выходной величины от виртуальной работы, имеющей гиперболический ха-
рактер, объяснимый природой процесса (смотри рисунок 4.4). Прилагая все
большие ресурсы управления (увеличивая виртуальную работу управления),
можно уменьшить дисперсию управляемой величины до сколь угодно малого
значения (однако не до нуля). Наоборот, уменьшая ресурсы, направляемые на
управление, приходим к увеличению дисперсии вплоть до бесконечности.
Имея зависимости дисперсии управляемой величины от виртуальной ра-
боты по управлению, можно оптимально распределить ресурсы.
Классический критерий оптимизации обычно принимают в следующем
виде /21/
()
()
]duK)(u),Y(L[M)]t,Y(l[MI
k
o
t
t
1T
k10
ττττ
∫
−
++= , (4.29)
где L(Y, t), l
1
(Y, t
k
) – заданные положительно определенные функции,
К – симметричная положительно определенная или диагональная

72
матрица положительных коэффициентов.
Считая данный функционал отражающим потери в метасистеме, при-
мем, что
)t,Y(l
k1
= 0, функция
L
зависит не от управляемых величин, а от их
дисперсий, а вместо обычной работы управляющих воздействий использует-
ся виртуальная:
Решая задачу оптимального управления метасистемой параллельного
действия с данным функционалом, можно определить установившиеся опти-
мальные значения дисперсий выходных величин. Для этого необходимо ре-
шить совместно систему, включающую уравнения (4.27), определение (4.28)
0 0.5 1 1.5 2 2.5
0
1
2
3
4
5
A σ()
σ
Рисунок 4.4 – Зависимость виртуальной работы от дисперсии
и критерий (4.30)
∑
∫
=
∞
+=
n
1i
t
iii
0
dt))t),t((A)t((MI
σσα
. (4.30)
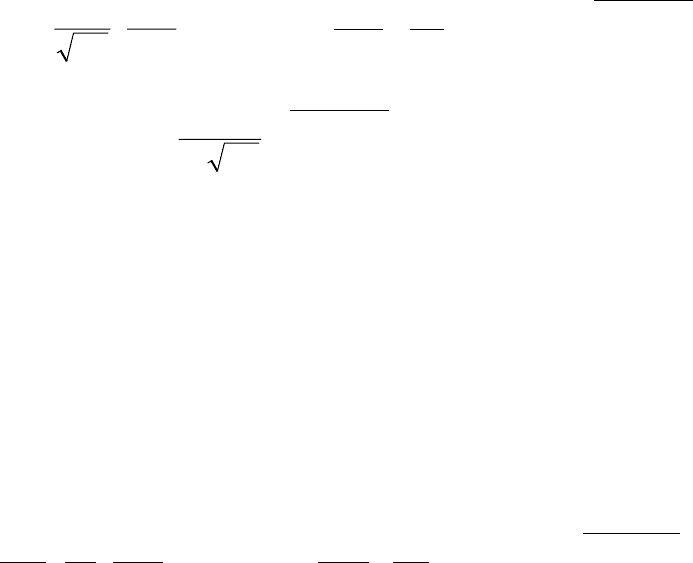
73
() ()
(
)
()
[]
→+
==
=
−−−−
∑
∫
=
∞
∞−
−
−
−
−
.min)(
,,,1,
2
)(
)(
),(
22
2
1
1
2
2
2
2
2
2
33
2
\
5
n
i
iiii
уст
yy
i
ii
i
ii
уст
yy
уст
i
i
i
i
уст
i
i
A
nidye
yu
A
yueyy
ab
yy
b
σσα
πσ
σ
σσσ
π
σ
σ
K (4.31)
Продифференцировав последнее уравнение по всем
i
σ
и приравняв эти
производные нулю, получим новую систему из n уравнений. В неё подставим
выражение виртуальной работы из второго уравнения системы (4.31), в кото-
рую, в свою очередь, подставлено управляющее воздействие из первого
уравнения системы (4.31). Окончательно получим n уравнений вида
ni
dyeyy
ab
yy
b
i
уст
yy
уст
i
i
i
i
уст
i
i
ii
,,1
2)(
2
)(
2
1
2
2
)(
33
2
5
K=
−=
−−−−
∂
∂
∫
∞
∞−
−
−
πα
σσσ
σσ
σ
.(4.32)
Решение этих уравнений определяет оптимальные нормы для дисперсий.
Дальнейшее управление можно свести к работе конечного автомата, который
будет перераспределять управляющие ресурсы с "благополучных" структур
на "неблагополучные" (то есть на те структуры, дисперсия выходных вели-
чин которых больше всего возросла). Все варианты распределения управ-
ляющих воздействий (состояний конечного автомата) можно описать сле-
дующей матрицей:
−
−
−
=
,...,u,u
u,...,,u
u,...,u,
U
2n1n
n221
n112
∆∆
∆∆
∆∆
∆
L
. (4.33)
Здесь номера столбцов соответствуют номерам структур, с которых
управляющие ресурсы "снимаются", а номера строк соответствуют номерам
структур, на которые управляющие воздействия направляются. Чертой поме-
чены неиспользуемые состояния.
Так будет работать система, у которой каждая структура имеет незави-
симый источник управляющего воздействия. При общем источнике парал-
лельная система может превратиться в последовательную (как отмечено вы-
ше). В этом случае управляющие ресурсы в любой момент времени подклю-
чаются автоматом лишь к одной структуре. Тогда можно применить теорию
систем случайной структуры и, вычислив вероятности включения каждой

74
структуры, использовать их в качестве уставок для конечного автомата (пре-
вратив тем самым автомат Мура в автомат Мили с обратной связью), что
увеличит точность работы системы.
Такое решение несправедливо для многосвязной системы. Рассмотрим
подробнее процесс перераспределения ресурсов. Положим для простоты ана-
лиза, что описанная выше зависимость имеет для двух управляемых величин
самый простой вид
Α
=Σ
Α
=Σ
β
α
21
, , (4.34)
где
β
α
,- размерные коэффициенты.
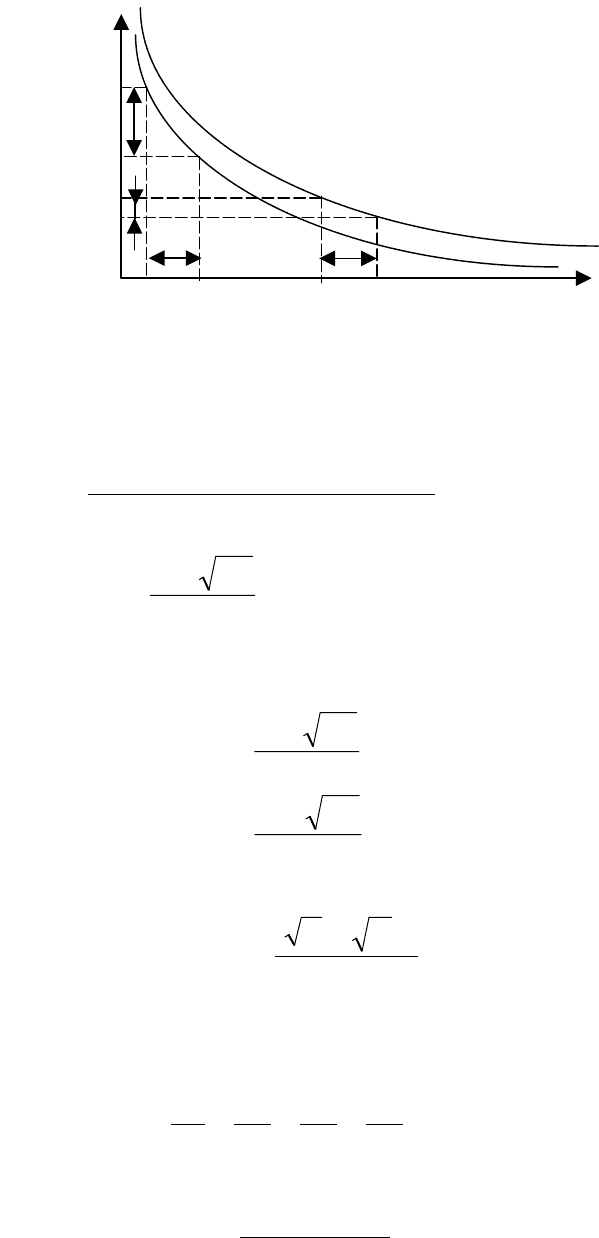
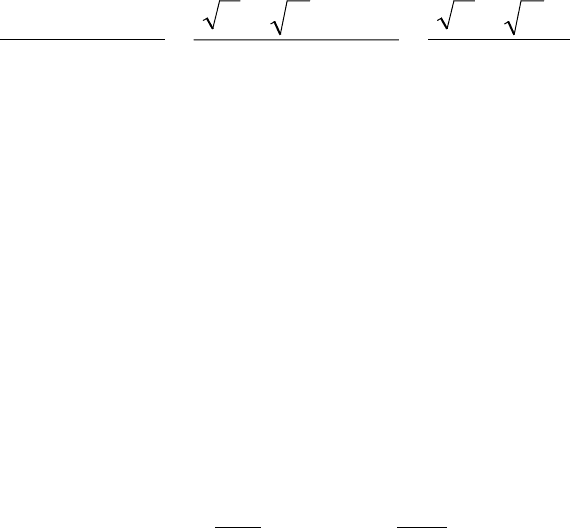
График этой зависимости изображен на рисунке 4.5.
Управление необходимо вести таким образом, чтобы суммарная диспер-
сия была минимальна
∑
=
→=
N
i
i
K
1
min
σ
. (4.35)
При этом можно провести двухуровневое управление с доведением
управляемых параметров до области нормированных значений, а затем, ис-
пользуя координацию управляющих воздействий, свести к минимуму крите-
рий
К /30/. Забирая малую долю ресурса от второго параметра и вкладывая ее
в улучшение первого, мы получим уменьшение суммы двух дисперсий
управляемых величин на величину
21
∆
Σ
−
∆
Σ . (4.36)
Такое перераспределение ресурса рационально, пока данная разность
положительна. Равенство отнимаемых и добавляемых ресурсов дает уравне-
ние для нахождения точек оптимальности
*
2
*
1
,
σσ
2
*
2
*
1
1
σ
β
σ
β
σ
α
σ
α
−=−
. (4.37)
Вводя обозначение для начальной суммы
C=+
21
σ
β
σ
α
, можно выразить
одно оптимальное значение через другое
ασ
βσ
σ
−
=
*
1
*
1
*
2
C
, (4.38)
Цель оптимизации теперь формулируется следующим образом
min
*
1
*
1
*
1
→
−
+
ασ
βσ
σ
C
. (4.39)
Взяв производную от этой суммы по
σ
1
*
и приравнивая ее нулю, найдем
оптимальное значение
75
σ
1
∆Σ
1
∆Σ
2
σ
2
∆A ∆A A
Виртуальная работа
Рисунок 4.5 – Схема перераспределения управляющих ресурсов
()
()
()
.
;0
2
*
1
2
*
1
*
1
2
*
1
2
C
C
CC
αβα
σ
ασ
αβαασσ
±
=
=
−
−−−
(4.40)
Считая коэффициенты 1>
α
и 1>
β
и учитывая, что
*
1
σ
всегда положи-
тельно, имеем единственное решение
+
=
+
=
.
;
*
2
*
1
C
C
αββ
σ
αβα
σ
(4.41)
При этом минимальная сумма равна
(
)
C
2
*
2
*
1
βα
σσ
+
=+ . (4.42)
Если бы мы потребовали совпадения точек оптимальности, то уравнение
(4.37) приняло бы вид:
2
**
1
σ
β
σ
β
σ
α
σ
α
−=− . (4.43)
Его решение
(
)
12
21
*
βσασ
σ
σ
β
α
σ
+
+
= . (4.44)
При этом минимальная сумма равна 2σ
*
.
Д
и
с
п
ерс
ия
76
Определяя разность двух минимальных сумм, убеждаемся, что она по-
ложительна
()
(
)
(
)
0
2
12
2
12
21
2
12
21
>
+
−
=
+
+
−
+
+
βσασ
βα
βσασ
σσβα
βσασ
σσβα
. (4.45)
Если погрешность, равная этой разности для двух параметров устраива-
ет проектировщика системы, то можно, последовательно добавляя опасности
отклонений следующих параметров, определить единственное псевдоопти-
мальное значение
σ
*
и минимальную сумму
.
*
1
*
σσ
N
N
i
i
=
∑
=
(4.46)
Находя разность этого значения
σ
*
с каждой опасностью отклонения,
можно добиться раздельного поканального управления подсистемами.
Если же эта разность нас не устраивает, тогда проведем более тонкое ис-
следование. Очевидно, что перераспределение управляющих ресурсов можно
прекратить, когда разность (4.36) равна 0.
Ограничиваясь конечными приращениями
;
1
1
∆Α
Α
∂
Σ
∂
=∆Σ ,
2
2
∆Α
Α
∂
Σ
∂
=∆Σ (4.47)
видим, что перераспределение ресурсов дает эффект, пропорциональный ча-
стным производным. В таком случае можно организовать следующий алго-
ритм.
1 Вычислить частные производные дисперсий всех управляемых вели-
чин по ресурсу в данных точках (
σ
1
,
σ
2
…
σ
N
).
2 Отсортировать производные в порядке убывания.
3 Перераспределить ресурс величиной ∆А от управления параметром с
максимальным значением производной на управление параметром с мини-
мальной производной.
4 Пересчитать производные, изменившиеся в результате выполнения
п.3.
5 Определить максимальную разность производных (max-min) и, если
она больше некоторого значения δ, перейти к п. 2.
6 Конец работы.
Значение δ определяется здесь по минимальному изменению производ-
ной на краю диапазона при заданном изменении ресурса ∆А. Этот алгоритм
работает тем точнее, чем ∆А меньше. Однако, при этом возрастает время его
работы.
Таким образом, при проведении такой координации мы сводим суммар-
ную дисперсию управляемых величин к минимуму или можем экономить ре-
сурсы управляющих воздействий (в зависимости от того, что выгоднее).
77
4.5 Экспериментальное исследование параллельной метасистемы
Модель такой системы включала три параллельно действующих регуля-
тора, характеризующихся систематической погрешностью a
i
и среднеквадра-
тичным разбросом
i
b , где i=1,2,3. Изменение во времени плотности рас-
пределения управляемой величины
i
ω
подчиняется уравнениям Фоккера-
Планка-Колмогорова
i
i
ii
i
i
i
i
u
y
b
y
a
t
=
∂
∂
−
∂
∂
+
∂
∂
2
2
2
ωωω
, (4.48)
где y
i
–управляемая величина,
u
i
– управляющее воздействие, изменяющее точность регуляторов (под-
настройка, подналадка).
Выше было проведено решение задачи непрерывного управления дис-
персией управляемой величины. Однако на практике поднастройка регулято-
ров проводится в импульсном режиме, то есть время от времени. Подставляя
импульсное воздействие в правую часть уравнения (4.48), найдем его реше-
ние
(
)
−
−−=
tb
yy
tb
t
b
a
y
b
a
i
i
moi
i
i
i
i
i
i
i
4
exp
2
1
)exp(
2
2
π
ω
. (4.49)
Как видим, результирующее решение представляет собой нормальный
закон с изменяющимся во времени среднеквадратичным отклонением (СКО)
(в зависимости только от параметра
i
b ) и сносом по оси y
i
(в зависимости
только от
i
a ).
Осредненное СКО за некоторый промежуток времени можно вычислить
по следующей формуле:
(
)
()
tT
tbTb
db
tT
ii
T
t
iср
−
−
=
∫
−
=
3
222
2
1
ττσ
. (4.50)
Процесс импульсного управления моделировался на компьютере при
следующих параметрах: a =1, b =1,
mo
y =1,
ср
σ
=1.
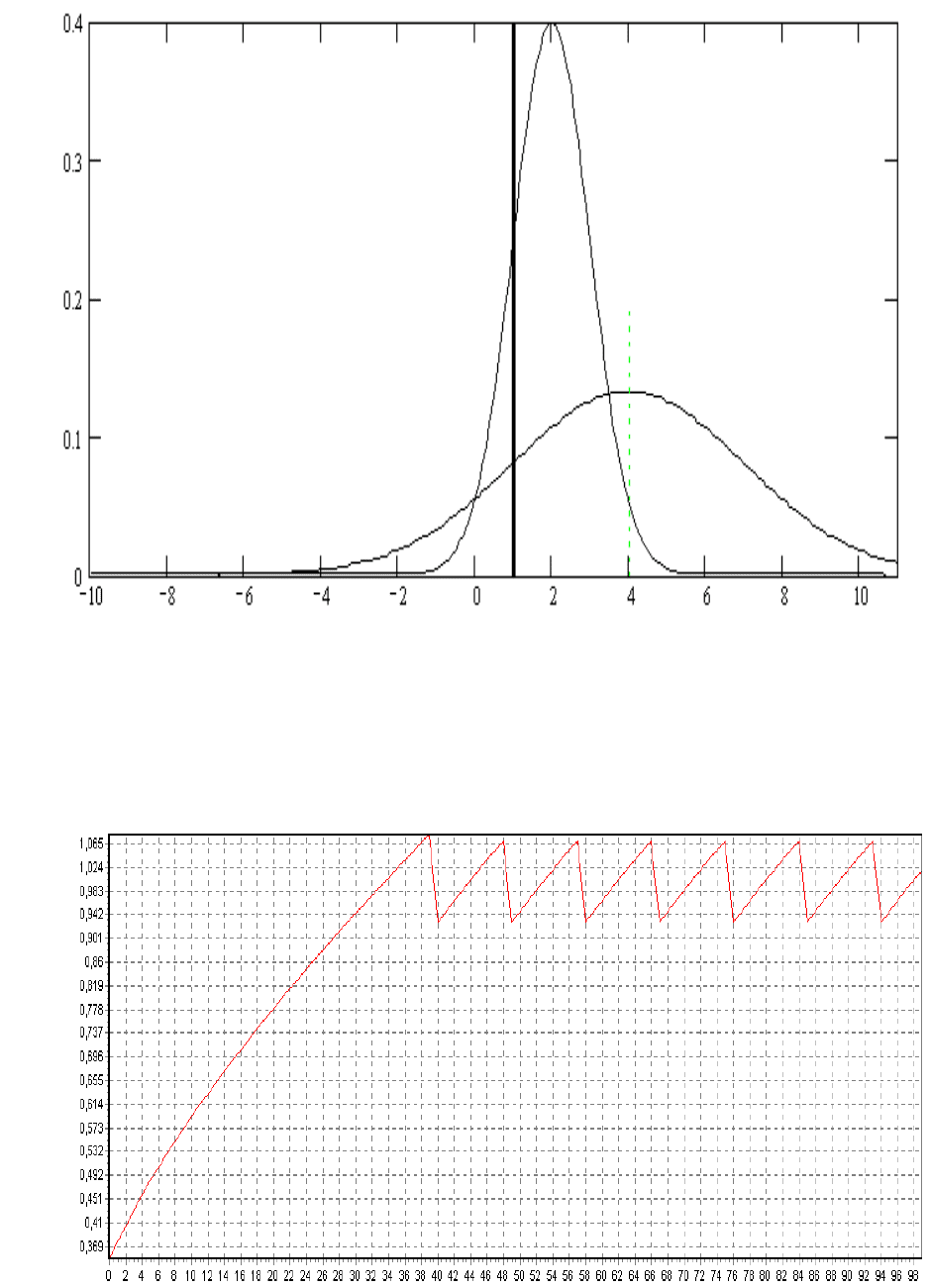
В отсутствии управляющих воздействий плотность распределения изме-
ренной величины подвержена сносу и размытию, как показано на рисунке
4.6.
Характер изменения СКО во времени при импульсной поднастройке
представлен на рисунке 4.7. По горизонтальной оси на рисунке отложен но-
мер шага по времени (03.0=∆
t
сек).
Для ответа на вопрос об оптимальной частоте поднастроек менялся пе-
риод их повторения, одновременно вычислялась виртуальная работа с ис-
пользованием зависимости, изображенной на рисунке 4.5.
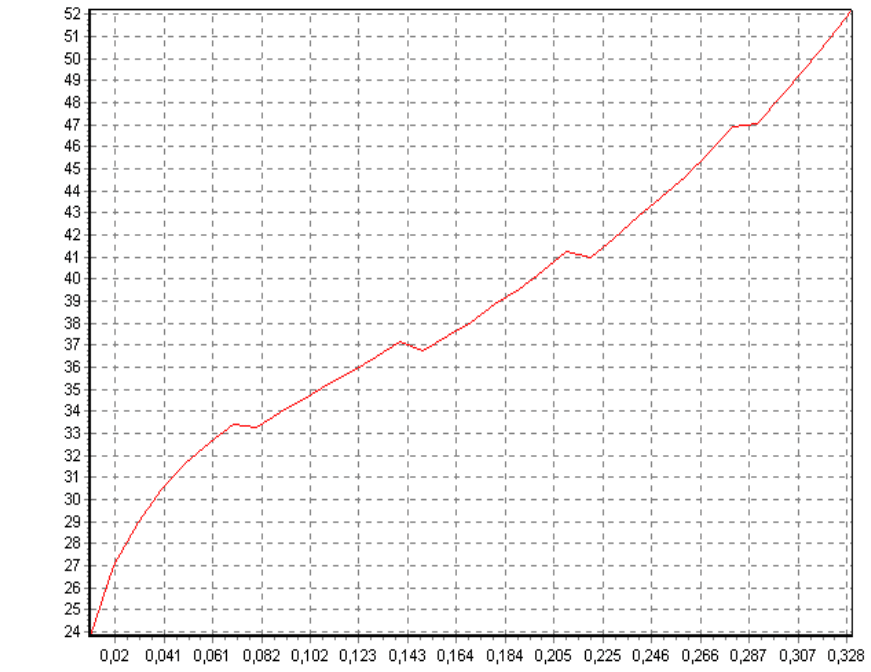
При этом была получена новая зависимость виртуальной работы от
длительности периода, изображенная на рисунке 4.8.
78
Изломы на графике обусловлены попаданием целого числа периодов в
расчетное время. Как следует из данной зависимости, минимальная суммар-
ная виртуальная работа имеет место при непрерывном управлении (нулевая
длительность периода). С ростом длительности периода между поднастрой-
ками приборов трудоемкость обслуживания комплекса измерительных при-
боров резко возрастает.
Если же метасистема является многосвязной, а не многомерной как в
предыдущем исследовании, то задача уже не поддается аналитическому ре-
шению.
В этом случае необходимо синтезировать конечный автомат, работаю-
щий по алгоритму, описанному в предыдущем разделе, и его функциониро-
вание позволит определить оптимальные значения дисперсий управляемых
величин.
Многосвязность моделировалась здесь следующим образом. Считалось,
что второй и третий регуляторы имеют положительное влияние на первый
(уровень перетекания управляющих воздействий везде принимался равным
10%). Первый и второй регуляторы отрицательно влияют на третий. Нако-
нец, первый регулятор положительно влияет на второй, а третий - отрица-
тельно. Результаты такого эксперимента представлены на рисунке 4.9. На
графике выделяются три области. Первая – область независимой работы ре-
гуляторов (дисперсия возрастает во всех трех каналах одинаково). Во второй
области вводится описанная выше взаимосвязь регуляторов, что приводит к
79
Значения управляемой величины
Рисунок 4.6 - Размытие плотности вероятности управляемой величины в
отсутствии поднастройки
время
Рисунок 4.7 - Изменение СКО во времени при импульсной поднастройке
Плотность ве
р
оятности
Дисперсия
80
Период
Рисунок 4.8 - Зависимость виртуальной работы от длительности периода ме-
жду поднастройками
Ви
р
т
у
альная
р
абота
