Munson B.R. Fundamentals of Fluid Mechanics

Подождите немного. Документ загружается.

variables to form a pi term. All of the required reference dimensions must be included

within the group of repeating variables, and each repeating variable must be dimension-

ally independent of the others 1i.e., the dimensions of one repeating variable cannot be

reproduced by some combination of products of powers of the remaining repeating vari-

ables2. This means that the repeating variables cannot themselves be combined to form

a dimensionless product.

For any given problem we usually are interested in determining how one partic-

ular variable is influenced by the other variables. We would consider this variable to be

the dependent variable, and we would want this to appear in only one pi term. Thus, do

not choose the dependent variable as one of the repeating variables, since the repeating

variables will generally appear in more than one pi term.

Step 5 Form a pi term by multiplying one of the nonrepeating variables by the product of

the repeating variables, each raised to an exponent that will make the combination

dimensionless. Essentially each pi term will be of the form where is one of

the nonrepeating variables; and are the repeating variables; and the exponents

and are determined so that the combination is dimensionless.

Step 6 Repeat Step 5 for each of the remaining nonrepeating variables. The resulting set of

pi terms will correspond to the required number obtained from Step 3. If not, check your

work—you have made a mistake!

Step 7 Check all the resulting pi terms to make sure they are dimensionless. It is easy to make

a mistake in forming the pi terms. However, this can be checked by simply substituting

the dimensions of the variables into the pi terms to confirm that they are all dimension-

less. One good way to do this is to express the variables in terms of M, L, and T if the

basic dimensions F, L, and T were used initially, or vice versa, and then check to make

sure the pi terms are dimensionless.

Step 8 Express the final form as a relationship among the pi terms, and think about what

it means. Typically the final form can be written as

where would contain the dependent variable in the numerator. It should be emphasized

that if you started out with the correct list of variables 1and the other steps were completed

correctly2, then the relationship in terms of the pi terms can be used to describe the prob-

lem. You need only work with the pi terms—not with the individual variables. However, it

should be clearly noted that this is as far as we can go with the dimensional analysis; that

is, the actual functional relationship among the pi terms must be determined by experiment.

To illustrate these various steps we will again consider the problem discussed earlier in this

chapter which was concerned with the steady flow of an incompressible Newtonian fluid through

a long, smooth-walled, horizontal circular pipe. We are interested in the pressure drop per unit

length, along the pipe as illustrated by the figure in the margin. First (Step 1) we must list

all of the pertinent variables that are involved based on the experimenter’s knowledge of the prob-

lem. In this problem we assume that

where D is the pipe diameter, and are the fluid density and viscosity, respectively, and V is the

mean velocity.

Next 1Step 22we express all the variables in terms of basic dimensions. Using F, L, and T

as basic dimensions it follows that

V ⬟ LT

⫺1

m ⬟ FL

⫺2

r ⬟ FL

⫺4

D ⬟ L

¢p

⬟ FL

⫺3

¢p

⫽ f1D, r, m, V2

¢p

⫽ f1ß

, ß

, . . . , ß

k⫺r

, b

, u

7.3 Determination of Pi Terms 337

By using dimen-

sional analysis, the

original problem is

simplified and de-

fined with pi terms.

(1) (2)

ρ, μ

ᐉ

Δp

ᐉ

= (p

– p

)/ᐉ

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 337

We could also use M, L, and T as basic dimensions if desired—the final result will be the same.

Note that for density, which is a mass per unit volume we have used the relationship

to express the density in terms of F, L, and T. Do not mix the basic dimensions; that

is, use either F, L, and T or M, L, and T.

We can now apply the pi theorem to determine the required number of pi terms 1Step 32. An

inspection of the dimensions of the variables from Step 2 reveals that all three basic dimensions

are required to describe the variables. Since there are five variables 1do not forget to count

the dependent variable, 2and three required reference dimensions then according to

the pi theorem there will be or two pi terms required.

The repeating variables to be used to form the pi terms 1Step 42need to be selected from the

list and V. Remember, we do not want to use the dependent variable as one of the repeat-

ing variables. Since three reference dimensions are required, we will need to select three repeating

variables. Generally, we would try to select as repeating variables those that are the simplest, di-

mensionally. For example, if one of the variables has the dimension of a length, choose it as one

of the repeating variables. In this example we will use D, V, and as repeating variables. Note

that these are dimensionally independent, since D is a length, V involves both length and time, and

involves force, length, and time. This means that we cannot form a dimensionless product from

this set.

We are now ready to form the two pi terms 1Step 52. Typically, we would start with the depen-

dent variable and combine it with the repeating variables to form the first pi term; that is,

Since this combination is to be dimensionless, it follows that

The exponents, a, b, and c must be determined such that the resulting exponent for each of the ba-

sic dimensions—F, L, and T—must be zero 1so that the resulting combination is dimensionless2.

Thus, we can write

The solution of this system of algebraic equations gives the desired values for a, b, and c. It fol-

lows that and, therefore,

The process is now repeated for the remaining nonrepeating variables 1Step 62. In this exam-

ple there is only one additional variable so that

and, therefore,

Solving these equations simultaneously it follows that so that

⫽

DVr

a ⫽⫺1, b ⫽⫺1, c ⫽⫺1

1 ⫺ b ⫹ 2c ⫽ 0

1for T2

⫺2 ⫹ a ⫹ b ⫺ 4c ⫽ 0

1for L2

1 ⫹ c ⫽ 0

1for F2

1FL

⫺2

T21L2

1LT

⫺1

1FL

⫺4

⬟ F

⫽ mD

1m2

⫽

¢p

a ⫽ 1, b ⫽⫺2, c ⫽⫺1

⫺b ⫹ 2c ⫽ 0

1for T2

⫺3 ⫹ a ⫹ b ⫺ 4c ⫽ 0

1for L2

1 ⫹ c ⫽ 0

1for F2

1FL

⫺3

21L2

1LT

⫺1

1FL

⫺4

⬟ F

⫽ ¢p

D, r, m,

15 ⫺ 32,

1r ⫽ 32,¢p

1k ⫽ 52

F ⬟ MLT

⫺2

1ML

⫺3

338 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

Special attention

should be given to

the selection of re-

peating variables as

detailed in Step 4.

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 338

Note that we end up with the correct number of pi terms as determined from Step 3.

At this point stop and check to make sure the pi terms are actually dimensionless 1Step 72.

We will check using both FLT and MLT dimensions. Thus,

or alternatively,

Finally 1Step 82, we can express the result of the dimensional analysis as

This result indicates that this problem can be studied in terms of these two pi terms, rather than

the original five variables we started with. The eight steps carried out to obtain this result are sum-

marized by the figure in the margin.

Dimensional analysis will not provide the form of the function This can only be obtained

from a suitable set of experiments. If desired, the pi terms can be rearranged; that is, the recipro-

cal of could be used, and of course the order in which we write the variables can be changed.

Thus, for example, could be expressed as

and the relationship between and as

as shown by the figure in the margin.

This is the form we previously used in our initial discussion of this problem 1Eq. 7.22. The

dimensionless product is a very famous one in fluid mechanics—the Reynolds number.

This number has been briefly alluded to in Chapters 1 and 6 and will be further discussed in Sec-

tion 7.6.

To summarize, the steps to be followed in performing a dimensional analysis using the method

of repeating variables are as follows:

Step 1 List all the variables that are involved in the problem.

Step 2 Express each of the variables in terms of basic dimensions.

Step 3 Determine the required number of pi terms.

Step 4 Select a number of repeating variables, where the number required is equal to the num-

ber of reference dimensions 1usually the same as the number of basic dimensions2.

Step 5 Form a pi term by multiplying one of the nonrepeating variables by the product of

repeating variables each raised to an exponent that will make the combination

dimensionless.

Step 6 Repeat Step 5 for each of the remaining nonrepeating variables.

Step 7 Check all the resulting pi terms to make sure they are dimensionless and independent.

Step 8 Express the final form as a relationship among the pi terms and think about what it

means.

rVD



D ¢p

 f a

rVD



rVD



DVr

¢p

 f

˜ a

DVr



DVr

⬟

1ML

1

1L21LT

1

21ML

3

⬟ M



¢p

⬟

1ML

2

21L2

1ML

3

21LT

1

⬟ M



DVr

⬟

1FL

2

1L21LT

1

21FL

4

⬟ F



¢p

⬟

1FL

3

21L2

1FL

4

21LT

1

⬟ F

7.3 Determination of Pi Terms 339

_____

DΔp

ᐉ

______

The method of re-

peating variables

can be most easily

carried out by fol-

lowing a step-by-

step procedure.

Δp

ᐉ

_____

= F

Step 1

Δp

ᐉ

= f(D, r, m , V)

Step 2

Δp

ᐉ

= FL

3

, ...

Step 3

k–r = 3

Step 4

D, V, r

Step 5



= Δp

ᐉ

Step 6



= mD

Step 7

Step 8

ᐉ

_____

= ␾

 

____

DVρ

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 339

340 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

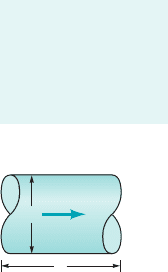
GIVEN A thin rectangular plate having a width w and a height

h is located so that it is normal to a moving stream of fluid as

shown in Fig. E7.1. Assume the drag, d, that the fluid exerts on

the plate is a function of w and h, the fluid viscosity and density,

␮ and ␳, respectively, and the velocity V of the fluid approaching

the plate.

OLUTION

F I G U R E E7.1

Method of Repeating Variables

XAMPLE 7.1

From the statement of the problem we can write

where this equation expresses the general functional relationship

between the drag and the several variables that will affect it. The

dimensions of the variables 1using the MLT system2are

We see that all three basic dimensions are required to define the

six variables so that the Buckingham pi theorem tells us that three

pi terms will be needed 1six variables minus three reference di-

mensions,

We will next select three repeating variables such as w,V, and

A quick inspection of these three reveals that they are dimensionally

independent, since each one contains a basic dimension not included

in the others. Note that it would be incorrect to use both w and h as

repeating variables since they have the same dimensions.

Starting with the dependent variable, the first pi term can

be formed by combining with the repeating variables such that

and in terms of dimensions

Thus, for to be dimensionless it follows that

and, therefore, and The pi term then

becomes

Next the procedure is repeated with the second nonrepeating

variable, h, so that

⫽ hw

⫽

c ⫽⫺1.a ⫽⫺2, b ⫽⫺2,

⫺2 ⫺ b ⫽ 0

1for T 2

1 ⫹ a ⫹ b ⫺ 3c ⫽ 0

1for L2

1 ⫹ c ⫽ 0

1for M2

1MLT

⫺2

21L2

1LT

⫺1

1ML

⫺3

⬟ M

⫽ dw

k ⫺ r ⫽ 6 ⫺ 32.

V ⬟ LT

⫺1

r ⬟ ML

⫺3

m ⬟ ML

⫺1

h ⬟ L

w ⬟ L

d ⬟ MLT

⫺2

d ⫽ f1w, h, m, r, V 2

V7.2 Flow past a

flat plate

FIND Determine a suitable set of pi terms to study this prob-

lem experimentally.

It follows that

and

so that and therefore

The remaining nonrepeating variable is so that

with

and, therefore,

Solving for the exponents, we obtain so

that

Now that we have the three required pi terms we should check

to make sure they are dimensionless. To make this check we use

F, L, and T, which will also verify the correctness of the original

dimensions used for the variables. Thus,

⫽

wVr

⬟

1FL

⫺2

1L21LT

⫺1

21FL

⫺4

⬟ F

⫽

⬟

1L2

⬟ F

⫽

⬟

1F2

1L2

1LT

⫺1

1FL

⫺4

⬟ F

⫽

wVr

a ⫽⫺1, b ⫽⫺1, c ⫽⫺1

⫺1 ⫺ b ⫽ 0

1for T2

⫺1 ⫹ a ⫹ b ⫺ 3c ⫽ 0

1for L2

1 ⫹ c ⫽ 0

1for M2

1ML

⫺1

21L2

1LT

⫺1

1ML

⫺3

⬟ M

⫽ mw

⫽

a ⫽⫺1, b ⫽ 0, c ⫽ 0,

b ⫽ 0

1for T 2

1 ⫹ a ⫹ b ⫺ 3c ⫽ 0

1for L2

c ⫽ 0

1for M2

1L21L2

1LT

⫺1

1ML

⫺3

⬟ M

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 340

7.4 Some Additional Comments about Dimensional Analysis 341

If these do not check, go back to the original list of variables and

make sure you have the correct dimensions for each of the vari-

ables and then check the algebra you used to obtain the exponents

a, b, and c.

Finally, we can express the results of the dimensional analysis

in the form

(Ans)

Since at this stage in the analysis the nature of the function is

unknown, we could rearrange the pi terms if we so desire. For

⫽ f

wVr

example, we could express the final result in the form

(Ans)

which would be more conventional, since the ratio of the plate

width to height, is called the aspect ratio, and is the

Reynolds number.

COMMENT To proceed, it would be necessary to perform a

set of experiments to determine the nature of the function , as

discussed in Section 7.7.

rVw

Ⲑ

⫽ f a

rVw

The preceding section provides a systematic approach for performing a dimensional analysis. Other

methods could be used, although we think the method of repeating variables is the easiest for the

beginning student to use. Pi terms can also be formed by inspection, as is discussed in Section 7.5.

Regardless of the specific method used for the dimensional analysis, there are certain aspects of

this important engineering tool that must seem a little baffling and mysterious to the student 1and

sometimes to the experienced investigator as well2. In this section we will attempt to elaborate on

some of the more subtle points that, based on our experience, can prove to be puzzling to students.

7.4.1 Selection of Variables

One of the most important, and difficult, steps in applying dimensional analysis to any given prob-

lem is the selection of the variables that are involved. As noted previously, for convenience we will

use the term variable to indicate any quantity involved, including dimensional and nondimensional

constants. There is no simple procedure whereby the variables can be easily identified. Generally,

one must rely on a good understanding of the phenomenon involved and the governing physical

laws. If extraneous variables are included, then too many pi terms appear in the final solution, and

it may be difficult, time consuming, and expensive to eliminate these experimentally. If important

variables are omitted, then an incorrect result will be obtained; and again, this may prove to be

costly and difficult to ascertain. It is, therefore, imperative that sufficient time and attention be

given to this first step in which the variables are determined.

Most engineering problems involve certain simplifying assumptions that have an influence on

the variables to be considered. Usually we wish to keep the problem as simple as possible, perhaps

even if some accuracy is sacrificed. A suitable balance between simplicity and accuracy is a desirable

goal. How “accurate” the solution must be depends on the objective of the study; that is, we may be

only concerned with general trends and, therefore, some variables that are thought to have only a mi-

nor influence in the problem may be neglected for simplicity.

For most engineering problems 1including areas outside of fluid mechanics2, pertinent vari-

ables can be classified into three general groups—geometry, material properties, and external effects.

Geometry. The geometric characteristics can usually be described by a series of lengths

and angles. In most problems the geometry of the system plays an important role, and a sufficient

number of geometric variables must be included to describe the system. These variables can usu-

ally be readily identified.

Material Properties. Since the response of a system to applied external effects such as

forces, pressures, and changes in temperature is dependent on the nature of the materials involved

in the system, the material properties that relate the external effects and the responses must be in-

cluded as variables. For example, for Newtonian fluids the viscosity of the fluid is the property

that relates the applied forces to the rates of deformation of the fluid. As the material behavior be-

comes more complex, such as would be true for non-Newtonian fluids, the determination of ma-

terial properties becomes difficult, and this class of variables can be troublesome to identify.

7.4 Some Additional Comments about Dimensional Analysis

It is often helpful to

classify variables

into three groups—

geometry, material

properties, and ex-

ternal effects.

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 341

External Effects. This terminology is used to denote any variable that produces, or tends

to produce, a change in the system. For example, in structural mechanics, forces 1either concen-

trated or distributed2applied to a system tend to change its geometry, and such forces would need

to be considered as pertinent variables. For fluid mechanics, variables in this class would be re-

lated to pressures, velocities, or gravity.

The above general classes of variables are intended as broad categories that should be help-

ful in identifying variables. It is likely, however, that there will be important variables that do not

fit easily into one of the above categories and each problem needs to be carefully analyzed.

Since we wish to keep the number of variables to a minimum, it is important that all vari-

ables are independent. For example, if in a given problem we know that the moment of inertia

of the area of a circular plate is an important variable, we could list either the moment of in-

ertia or the plate diameter as the pertinent variable. However, it would be unnecessary to in-

clude both moment of inertia and diameter, assuming that the diameter enters the problem only

through the moment of inertia. In more general terms, if we have a problem in which the vari-

ables are

(7.3)

and it is known that there is an additional relationship among some of the variables, for example,

(7.4)

then q is not required and can be omitted. Conversely, if it is known that the only way the vari-

ables u, w, . . . enter the problem is through the relationship expressed by Eq. 7.4, then the

variables u, w, . . . can be replaced by the single variable q, therefore reducing the number of

variables.

In summary, the following points should be considered in the selection of variables:

1. Clearly define the problem. What is the main variable of interest 1the dependent variable2?

2. Consider the basic laws that govern the phenomenon. Even a crude theory that describes the

essential aspects of the system may be helpful.

3. Start the variable selection process by grouping the variables into three broad classes: geom-

etry, material properties, and external effects.

4. Consider other variables that may not fall into one of the above categories. For example, time

will be an important variable if any of the variables are time dependent.

5. Be sure to include all quantities that enter the problem even though some of them may be

held constant 1e.g., the acceleration of gravity, g2. For a dimensional analysis it is the dimen-

sions of the quantities that are important—not specific values!

6. Make sure that all variables are independent. Look for relationships among subsets of the

variables.

7.4.2 Determination of Reference Dimensions

For any given problem it is obviously desirable to reduce the number of pi terms to a minimum

and, therefore, we wish to reduce the number of variables to a minimum; that is, we certainly do

not want to include extraneous variables. It is also important to know how many reference dimen-

sions are required to describe the variables. As we have seen in the preceding examples, F, L, and

T appear to be a convenient set of basic dimensions for characterizing fluid-mechanical quantities.

There is, however, really nothing “fundamental” about this set, and as previously noted M, L, and

T would also be suitable. Actually any set of measurable quantities could be used as basic dimen-

sions provided that the selected combination can be used to describe all secondary quantities. How-

ever, the use of FLT or MLT as basic dimensions is the simplest, and these dimensions can be used

to describe fluid-mechanical phenomena. Of course, in some problems only one or two of these

are required. In addition, we occasionally find that the number of reference dimensions needed to

describe all variables is smaller than the number of basic dimensions. This point is illustrated in

Example 7.2. Interesting discussions, both practical and philosophical, relative to the concept of

basic dimensions can be found in the books by Huntley 1Ref. 42and by Isaacson and Isaacson

1Ref. 122.

q ⫽ f

1u, v, w, . . .2

f1p, q, r, . . . , u, v, w, . . .2⫽ 0

342 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

Typically, in fluid

mechanics, the re-

quired number of

reference dimen-

sions is three, but

in some problems

only one or two are

required.

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 342

7.4 Some Additional Comments about Dimensional Analysis 343

GIVEN An open, cylindrical paint can having a diameter D is

filled to a depth h with paint having a specific weight The ver-

tical deflection, of the center of the bottom is a function of D,

h, d, and E, where d is the thickness of the bottom and E is the

modulus of elasticity of the bottom material.

FIND Determine the functional relationship between the verti-

cal deflection, and the independent variables using dimensional

analysis.

OLUTION

F I G U R E E7.2

Determination of Pi Terms

Thus, this problem can be studied by using the relationship

(Ans)

COMMENTS Let us now solve the same problem using the

MLT system. Although the number of variables is obviously the

same, it would seem that there are three reference dimensions re-

quired, rather than two. If this were indeed true it would certainly

be fortuitous, since we would reduce the number of required pi

terms from four to three. Does this seem right? How can we re-

duce the number of required pi terms by simply using the MLT

system of basic dimensions? The answer is that we cannot, and a

closer look at the dimensions of the variables listed above reveals

that actually only two reference dimensions, and L, are

required.

This is an example of the situation in which the number of

reference dimensions differs from the number of basic dimen-

sions. It does not happen very often and can be detected by look-

ing at the dimensions of the variables 1regardless of the systems

used2and making sure how many reference dimensions are ac-

tually required to describe the variables. Once the number of

reference dimensions has been determined, we can proceed as

before. Since the number of repeating variables must equal the

number of reference dimensions, it follows that two reference

dimensions are still required and we could again use D and as

repeating variables. The pi terms would be determined in the

same manner. For example, the pi term containing E would be

developed as

⫺1 ⫹ a ⫺ 2b ⫽ 0

1for L2

1 ⫹ b ⫽ 0

1for MT

⫺2

1ML

⫺1

⫺2

21L2

1ML

⫺2

⬟ 1MT

⫺2

⫽ ED

⫺2

⫽ f a

E, d

XAMPLE 7.2

From the statement of the problem

and the dimensions of the variables are

where the dimensions have been expressed in terms of both the

FLT and MLT systems.

We now apply the pi theorem to determine the required num-

ber of pi terms. First, let us use F, L, and T as our system of basic

dimensions. There are six variables and two reference dimensions

1F and L2required so that four pi terms are needed. For repeating

variables, we can select D and so that

and

Therefore, and

Similarly,

and following the same procedure as above, so that

The remaining two pi terms can be found using the same proce-

dure, with the result

⫽

a ⫽⫺1, b ⫽ 0

⫽ h D

⫽

a ⫽⫺1, b ⫽ 0,

b ⫽ 0

1for F2

1 ⫹ a ⫺ 3b ⫽ 0

1for L2

1L21L2

1FL

⫺3

⬟ F

⫽ d D

E ⬟ FL

⫺2

⬟ ML

⫺1

⫺2

g ⬟ FL

⫺3

⬟ ML

⫺2

d ⬟ L

h ⬟ L

D ⬟ L

d ⬟ L

d ⫽ f1D, h, d, g, E2

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 343

7.4.3 Uniqueness of Pi Terms

A little reflection on the process used to determine pi terms by the method of repeating vari-

ables reveals that the specific pi terms obtained depend on the somewhat arbitrary selection of

repeating variables. For example, in the problem of studying the pressure drop in a pipe, we se-

lected D, V, and as repeating variables. This led to the formulation of the problem in terms of

pi terms as

(7.5)

What if we had selected D, V, and as repeating variables? A quick check will reveal that the pi

term involving becomes

and the second pi term remains the same. Thus, we can express the final result as

(7.6)

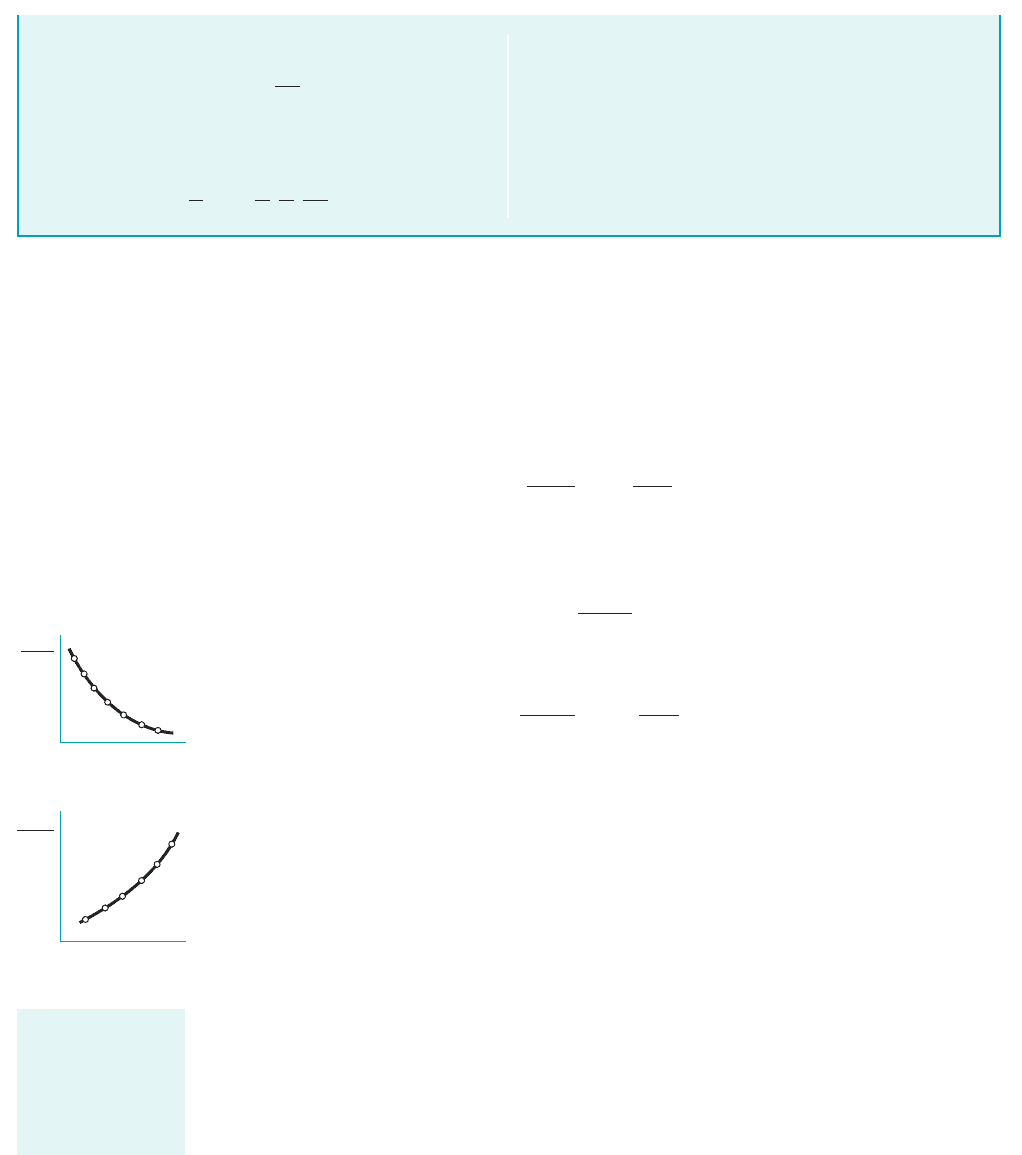
Both results are correct, and both would lead to the same final equation for . Note, however,

that the functions in Eqs. 7.5 and 7.6 will be different because the dependent pi terms

are different for the two relationships. As shown by the figure in the margin, the resulting graph

of dimensionless data will be different for the two formulations. However, when extracting the

physical variable, , from the two results, the values will be the same.

We can conclude from this illustration that there is not a unique set of pi terms which

arises from a dimensional analysis. However, the required number of pi terms is fixed, and once

a correct set is determined, all other possible sets can be developed from this set by combina-

tions of products of powers of the original set. Thus, if we have a problem involving, say, three

pi terms,

we could always form a new set from this one by combining the pi terms. For example, we could

form a new pi term, by letting

where a and b are arbitrary exponents. Then the relationship could be expressed as

All of these would be correct. It should be emphasized, however, that the required number of pi

terms cannot be reduced by this manipulation; only the form of the pi terms is altered. By using

⫽ f

1ß

, ß¿

⫽ f

1ß¿

, ß

ß¿

⫽ ß

ß¿

⫽ f1ß

, ß

¢p

f and f

¢p

⫽ f

rVD

¢p

⫽ f a

rVD

344 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

and, therefore, so that

which is the same as obtained using the FLT system. The other

pi terms would be the same, and the final result is the same; that is,

(Ans)

⫽ f a

⫽

a ⫽⫺1, b ⫽⫺1

This will always be true—you cannot affect the required number

of pi terms by using M, L, and T instead of F, L, and T, or vice

versa.

Once a correct set

of pi terms is ob-

tained, any other

set can be obtained

by manipulation of

the original set.

Δp

ᐉ

____

DΔp

ᐉ

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 344

this technique we see that the pi terms in Eq. 7.6 could be obtained from those in Eq. 7.5; that is,

we multiply in Eq. 7.5 by so that

which is the of Eq. 7.6.

There is no simple answer to the question: Which form for the pi terms is best? Usually our

only guideline is to keep the pi terms as simple as possible. Also, it may be that certain pi terms

will be easier to work with in actually performing experiments. The final choice remains an ar-

bitrary one and generally will depend on the background and experience of the investigator. It

should again be emphasized, however, that although there is no unique set of pi terms for a given

problem, the number required is fixed in accordance with the pi theorem.

¢p

b a

rVD

b⫽

¢p

7.5 Determination of Pi Terms by Inspection 345

The method of repeating variables for forming pi terms has been presented in Section 7.3. This

method provides a step-by-step procedure that if executed properly will provide a correct and com-

plete set of pi terms. Although this method is simple and straightforward, it is rather tedious, par-

ticularly for problems in which large numbers of variables are involved. Since the only restrictions

placed on the pi terms are that they be 112correct in number, 122dimensionless, and 132indepen-

dent, it is possible to simply form the pi terms by inspection, without resorting to the more formal

procedure.

To illustrate this approach, we again consider the pressure drop per unit length along a smooth

pipe. Regardless of the technique to be used, the starting point remains the same—determine the

variables, which in this case are

Next, the dimensions of the variables are listed:

and subsequently the number of reference dimensions determined. The application of the pi theo-

rem then tells us how many pi terms are required. In this problem, since there are five variables

and three reference dimensions, two pi terms are needed. Thus, the required number of pi terms

can be easily obtained. The determination of this number should always be done at the beginning

of the analysis.

Once the number of pi terms is known, we can form each pi term by inspection, simply mak-

ing use of the fact that each pi term must be dimensionless. We will always let contain the de-

pendent variable, which in this example is Since this variable has the dimensions we

need to combine it with other variables so that a nondimensional product will result. One possi-

bility is to first divide by so that

The dependence on F has been eliminated, but is obviously not dimensionless. To elimi-

nate the dependence on T, we can divide by so that

¢p

⬟ a

1LT

⫺1

⬟

1cancels T2

¢p

Ⲑ

¢p

⬟

1FL

⫺3

1FL

⫺4

⬟

1cancels F2

r¢p

⫺3

,¢p

V ⬟ LT

⫺1

m ⬟ FL

⫺2

r ⬟ FL

⫺4

D ⬟ L

¢p

⬟ FL

⫺3

¢p

⫽ f1D, r, m, V2

7.5 Determination of Pi Terms by Inspection

Pi terms can be

formed by inspec-

tion by simply mak-

ing use of the fact

that each pi term

must be dimension-

less.

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 345

Finally, to make the combination dimensionless we multiply by D so that

Thus,

Next, we will form the second pi term by selecting the variable that was not used in

which in this case is We simply combine with the other variables to make the combination

dimensionless 1but do not use in since we want the dependent variable to appear only in

2. For example, divide by 1to eliminate F2, then by V 1to eliminate T2, and finally by D 1to

eliminate L2. Thus,

and, therefore,

which is, of course, the same result we obtained by using the method of repeating variables.

An additional concern, when one is forming pi terms by inspection, is to make certain that

they are all independent. In the pipe flow example, contains which does not appear in ,

and therefore these two pi terms are obviously independent. In a more general case a pi term would

not be independent of the others in a given problem if it can be formed by some combination of

the others. For example, if can be formed by a combination of say and such as

then is not an independent pi term. We can ensure that each pi term is independent of those

preceding it by incorporating a new variable in each pi term.

Although forming pi terms by inspection is essentially equivalent to the repeating variable

method, it is less structured. With a little practice the pi terms can be readily formed by inspec-

tion, and this method offers an alternative to more formal procedures.

⫽

, ß

,ß

m,ß

¢p

⫽ f a

rVD

⫽

rVD

⬟

1FL

⫺2

1FL

⫺4

21LT

⫺1

21L2

⬟ F

rmß

,¢p

mm.

⫽

¢p

b D ⬟ a

b 1L2⬟ L

1cancels L2

346 Chapter 7 ■ Dimensional Analysis, Similitude, and Modeling

At the top of Table 7.1 is a list of variables that commonly arise in fluid mechanics problems.

The list is obviously not exhaustive but does indicate a broad range of variables likely to be found

in a typical problem. Fortunately, not all of these variables would be encountered in all prob-

lems. However, when combinations of these variables are present, it is standard practice to com-

bine them into some of the common dimensionless groups 1pi terms2given in Table 7.1. These

combinations appear so frequently that special names are associated with them, as indicated in

the table.

It is also often possible to provide a physical interpretation to the dimensionless groups which

can be helpful in assessing their influence in a particular application. For example, the Froude num-

ber is an index of the ratio of the force due to the acceleration of a fluid particle to the force due

to gravity 1weight2. This can be demonstrated by considering a fluid particle moving along a stream-

line 1Fig. 7.32. The magnitude of the component of inertia force along the streamline can be ex-

pressed as where is the magnitude of the acceleration along the streamline for a par-

ticle having a mass m. From our study of particle motion along a curved path 1see Section 3.12we

know that

⫽

⫽ V

⫽ a

7.6 Common Dimensionless Groups in Fluid Mechanics

A useful physical

interpretation can

often be given to di-

mensionless groups.

JWCL068_ch07_332-382.qxd 9/23/08 10:46 AM Page 346