Neamen D. Microelectronics: Circuit Analysis and Design

Подождите немного. Документ загружается.

208 Part 1 Semiconductor Devices and Basic Applications

discussed in the Prologue, but is repeated here for convenience. A lowercase letter

with an upper case subscript, such as

, indicates a total instantaneous value.

An uppercase letter with an uppercase subscript, such as I

, indicates a dc

quantity. A lowercase letter with a lowercase subscript, such as

and

, indicates

an instantaneous value of an ac signal. Finally, an uppercase letter with a lowercase

subscript, such as I

, indicates a phasor quantity. The phasor notation, which

is also reviewed in the Prologue, becomes especially important in Chapter 7 during

the discussion of frequency response. However, the phasor notation will generally be

used in this chapter in order to be consistent with the overall ac analysis.

From Figure 4.1, we see that the instantaneous gate-to-source voltage is

= V

GSQ

= V

GSQ

(4.1)

where V

GSQ

is the dc component and

is the ac component. The instantaneous

drain current is

= K

− V

)

(4.2)

Substituting Equation (4.1) into (4.2) produces

= K

GSQ

− V

]

= K

[(V

GSQ

− V

) + v

]

(4.3(a))

= K

GSQ

− V

)

+2K

GSQ

− V

+ K

(4.3(b))

The ﬁrst term in Equation (4.3(b)) is the dc or quiescent drain current I

, the

second term is the time-varying drain current component that is linearly related to the

signal v

, and the third term is proportional to the square of the signal voltage. For

a sinusoidal input signal, the squared term produces undesirable harmonics, or non-

linear distortion, in the output voltage. To minimize these harmonics, we require

 2(V

GSQ

− V

)

(4.4)

which means that the third term in Equation (4.3(b)) will be much smaller than the

second term. Equation (4.4) represents the small-signal condition that must be satis-

ﬁed for linear ampliﬁers.

Neglecting the

term, we can write Equation (4.3(b)) as

= I

(4.5)

Again, small-signal implies linearity so that the total current can be separated into

a dc component and an ac component. The ac component of the drain current is

given by

= 2K

GSQ

− V

(4.6)

The small-signal drain current is related to the small-signal gate-to-source volt-

age by the transconductance g

. The relationship is

= 2K

GSQ

− V

)

(4.7)

The transconductance is a transfer coefﬁcient relating output current to input voltage

and can be thought of as representing the gain of the transistor.

The transconductance can also be obtained from the derivative

∂i

∂v



GSQ

=const.

= 2K

GSQ

− V

)

(4.8(a))

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 208 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

Chapter 4 Basic FET Ampliﬁers 209

which can be written as

= 2



(4.8(b))

The drain current versus gate-to-source voltage for the transistor biased in the

saturation region is given in Equation (4.2) and is shown in Figure 4.3. The transcon-

ductance g

is the slope of the curve. If the time-varying signal v

is sufﬁciently

small, the transconductance g

is a constant. With the Q-point in the saturation

region, the transistor operates as a current source that is linearly controlled by v

. If

the Q-point moves into the nonsaturation region, the transistor no longer operates as

a linearly controlled current source.

As shown in Equation (4.8(a)), the transconductance is directly proportional to

the conduction parameter K

, which in turn is a function of the width-to-length ratio.

Therefore, increasing the width of the transistor increases the transconductance, or

gain, of the transistor.

Time

Slope = g

Figure 4.3 Drain current versus gate-to-source voltage characteristics, with superimposed

sinusoidal signals

EXAMPLE 4.1

Objective: Calculate the transconductance of an n-channel MOSFET.

Consider an n-channel MOSFET with parameters

= 0.4



= 100 μ

A/V

and

W/L = 25

. Assume the drain current is

= 0.40

mA.

Solution: The conduction parameter is



= (

0.1

)(25) = 1.25 mA/V

Assuming the transistor is biased in the saturation region, the transconductance is

determined from Equation (4.8(b)) as

= 2



= 2

√

(1.25)(0.4) = 1.41

mA/V

Comment: The value of the transconductance can be increased by increasing the

transistor

W/L

ratio and also by increasing the quiescent drain current.

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 209 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

210 Part 1 Semiconductor Devices and Basic Applications

EXERCISE PROBLEM

Ex 4.1: For an n-channel MOSFET biased in the saturation region, the parameters

are



= 100 μ

A/V

= 0.6

V, and

= 0.8

mA. Determine the transistor

width-to-length ratio such that the transconductance is

= 1.8

mA/V. (Ans. 20.25)

AC Equivalent Circuit

From Figure 4.l, we see that the output voltage is

= v

= V

−i

(4.9)

Using Equation (4.5), we obtain

= V

−(I

= (V

− I

) − i

(4.10)

The output voltage is also a combination of dc and ac values. The time-varying

output signal is the time-varying drain-to-source voltage, or

= v

=−i

(4.11)

Also, from Equations (4.6) and (4.7), we have

= g

(4.12)

In summary, the following relationships exist between the time-varying signals

for the circuit in Figure 4.1. The equations are given in terms of the instantaneous

ac values, as well as the phasors. We have

= v

= V

(4.13)

and

= g

(4.14)

and

=−i

=−I

(4.15)

The ac equivalent circuit in Figure 4.4 is developed by setting the dc sources in

Figure 4.l equal to zero. The small-signal relationships are given in Equations (4.13),

(4.14), and (4.15). As shown in Figure 4.l, the drain current, which is composed of ac

signals superimposed on the quiescent value, ﬂows through the voltage source

Since the voltage across this source is assumed to be constant, the sinusoidal current

produces no sinusoidal voltage component across this element. The equivalent ac

impedance is therefore zero, or a short circuit. Consequently, in the ac equivalent

circuit, the dc voltage sources are equal to zero. We say that the node connecting R

and

is at signal ground.

Small-Signal Equivalent Circuit

Now that we have the ac equivalent circuit for the NMOS ampliﬁer circuit, (Figure

4.4), we must develop a small-signal equivalent circuit for the transistor.

Initially, we assume that the signal frequency is sufﬁciently low so that any

capacitance at the gate terminal can be neglected. The input to the gate thus appears

as an open circuit, or an inﬁnite resistance. Equation (4.14) relates the small-signal

4.1.2

–

Figure 4.4 AC equivalent

circuit of common-source

ampliﬁer with NMOS

transistor

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 210 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

Chapter 4 Basic FET Ampliﬁers 211

(a) (b)

)

–

)

–

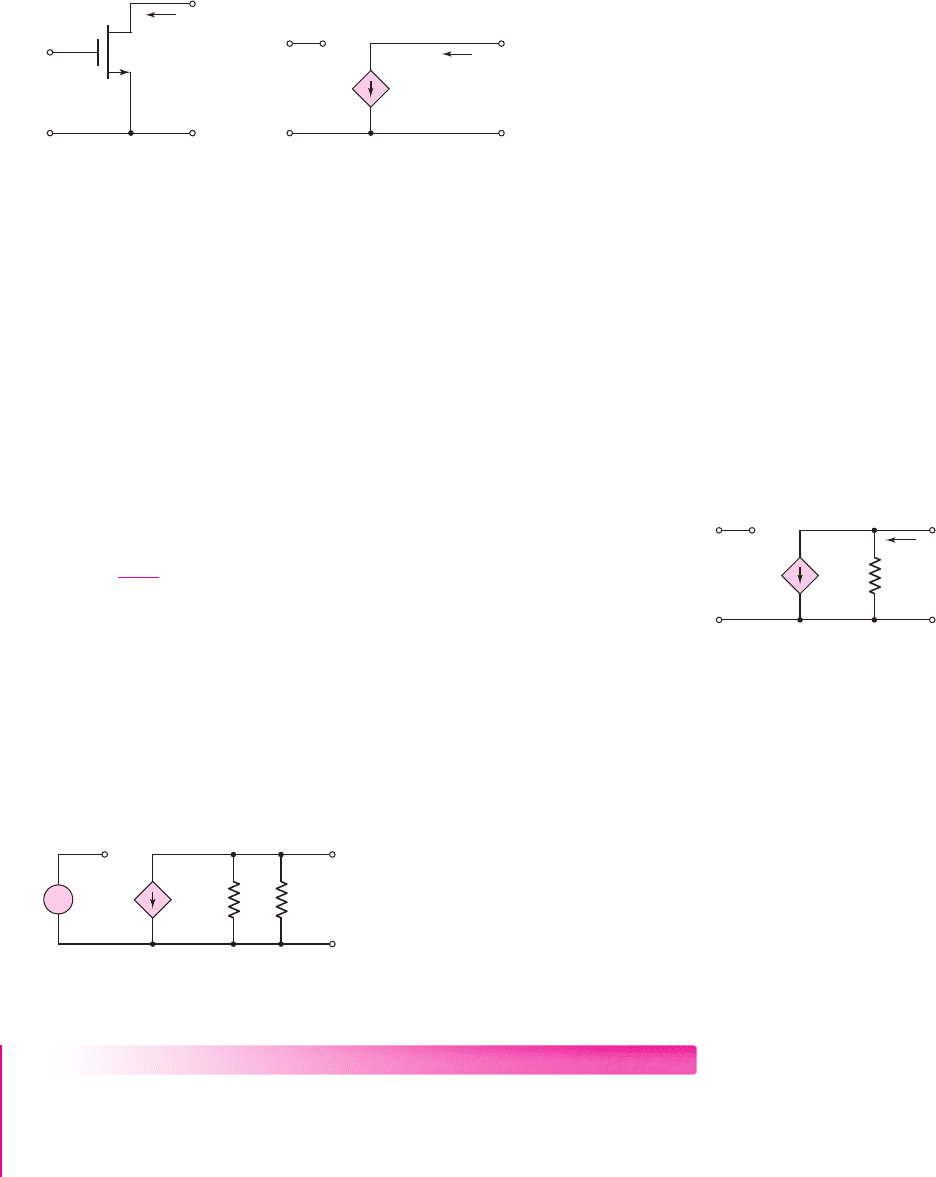
Figure 4.5 (a) Common-source NMOS transistor with small-signal parameters and

(b) simpliﬁed small-signal equivalent circuit for NMOS transistor

drain current to the small-signal input voltage, and Equation (4.7) shows that the

transconductance g

is a function of the Q-point. The resulting simpliﬁed small-

signal equivalent circuit for the NMOS device is shown in Figure 4.5. (The phasor

components are in parentheses.)

This small-signal equivalent circuit can also be expanded to take into account the

ﬁnite output resistance of a MOSFET biased in the saturation region. This effect, dis-

cussed in the last chapter, is a result of the nonzero slope in the i

versus

curve.

We know that

= K

[(v

− V

)

(1 + λv

)]

(4.16)

where

is the channel-length modulation parameter and is a positive quantity. The

small-signal output resistance, as previously deﬁned, is



∂i

∂v



−1



GSQ

=const.

(4.17)

= [λK

GSQ

− V

)

]

−1

∼

[λI

]

−1

(4.18)

This small-signal output resistance is also a function of the Q-point parameters.

The expanded small-signal equivalent circuit of the n-channel MOSFET is

shown in Figure 4.6 in phasor notation. Note that this equivalent circuit is a transcon-

ductance ampliﬁer in that the input signal is a voltage and the output signal is a

current. This equivalent circuit can now be inserted into the ampliﬁer ac equivalent

circuit in Figure 4.4 to produce the circuit in Figure 4.7.

–

Figure 4.6 Expanded small-

signal equivalent circuit,

including output resistance,

for NMOS transistor

Vgs

–

Figure 4.7 Small-signal equivalent circuit of common-source circuit with NMOS transistor

model

EXAMPLE 4.2

Objective: Determine the small-signal voltage gain of a MOSFET circuit.

For the circuit in Figure 4.l, assume parameters are:

GSQ

= 2.12

= 5

and

= 2.5



. Assume transistor parameters are:

= 1V. K

= 0.80

, and

λ = 0.02 V

−1

. Assume the transistor is biased in the saturation region.

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 211 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

212 Part 1 Semiconductor Devices and Basic Applications

Solution: The quiescent values are

∼

GSQ

− V

)

= (0.8)(2.12 −1)

= 1.0mA

and

DSQ

= V

− I

= 5 −(1)(2.5) = 2.5V

Therefore,

DSQ

= 2.5V> V

(sat) = V

− V

= 1.82 −1 = 0.82 V

which means that the transistor is biased in the saturation region, as initially

assumed, and as required for a linear ampliﬁer. The transconductance is

= 2K

GSQ

− V

) = 2(0.8)(2.12 −1) = 1.79 mA/V

and the output resistance is

= [λI

]

−1

= [(0.02)(1)]

−1

= 50 k

From Figure 4.7, the output voltage is

=−g

R

)

Since

= V

, the small-signal voltage gain is

=−g

R

) =−(1.79)(502.5) =−4.26

Comment: The magnitude of the ac output voltage is 4.26 times larger than the mag-

nitude of the input voltage. Hence, we have an ampliﬁer. Note that the small-signal

voltage gain contains a minus sign, which means that the sinusoidal output voltage is

180 degrees out of phase with respect to the input sinusoidal signal.

EXERCISE PROBLEM

Ex 4.2: For the circuit shown in Figure 4.1,

= 3.3

V and

= 10



. The

transistor parameters are

= 0.4



= 100 μ

A/V

W/L = 50

, and

λ = 0.025

−1

. Assume the transistor is biased such that

= 0.25

mA. (a) Verify

that the transistor is biased in the saturation region. (b) Determine the small-

signal parameters

and

. (c) Determine the small-signal voltage gain.

(Ans. (a)

GSQ

= 0.716

V and

DSQ

= 0.8

V so that

> V

(

sat

)

;

(b)

= 1.58

mA/V,

= 160



; (c)

−14.9)

Problem-Solving Technique: MOSFET AC Analysis

Since we are dealing with linear ampliﬁers, superposition applies, which means

that we can perform the dc and ac analyses separately. The analysis of the MOSFET

ampliﬁer proceeds as follows:

1. Analyze the circuit with only the dc sources present. This solution is the dc or

quiescent solution. The transistor must be biased in the saturation region in

order to produce a linear ampliﬁer.

2. Replace each element in the circuit with its small-signal model, which means

replacing the transistor by its small-signal equivalent circuit.

3. Analyze the small-signal equivalent circuit, setting the dc source components

equal to zero, to produce the response of the circuit to the time-varying input

signals only.

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 212 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

Chapter 4 Basic FET Ampliﬁers 213

(b)

–

(a)

–

Figure 4.8 (a) Common-source circuit with PMOS

transistor and (b) corresponding ac equivalent circuit

The previous discussion was for an n-channel MOSFET ampliﬁer. The same basic

analysis and equivalent circuit also applies to the p-channel transistor. Figure 4.8(a)

shows a circuit containing a p-channel MOSFET. Note that the power supply voltage

is connected to the source. (The subscript DD can be used to indicate that the

supply is connected to the drain terminal. Here, however,

is simply the usual

notation for the power supply voltage in MOSFET circuits.) Also note the change in

current directions and voltage polarities compared to the circuit containing the

NMOS transistor. Figure 4.8(b) shows the ac equivalent circuit, with the dc voltage

sources replaced by ac short circuits, and all currents and voltages shown are the time-

varying components.

In the circuit of Figure 4.8(b), the transistor can be replaced by the equivalent

circuit in Figure 4.9. The equivalent circuit of the p-channel MOSFET is the same as

that of the n-channel device, except that all current directions and voltage polarities

are reversed.

The ﬁnal small-signal equivalent circuit of the p-channel MOSFET ampliﬁer is

shown in Figure 4.10. The output voltage is

= g

R

)

(4.19)

The control voltage V

, given in terms of the input signal voltage, is

=−V

(4.20)

and the small-signal voltage gain is

=−g

R

)

(4.21)

–

Figure 4.9 Small-signal equivalent

circuit of PMOS transistor

–

Figure 4.10 Small-signal equivalent circuit of common-source ampliﬁer with PMOS

transistor model

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 213 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

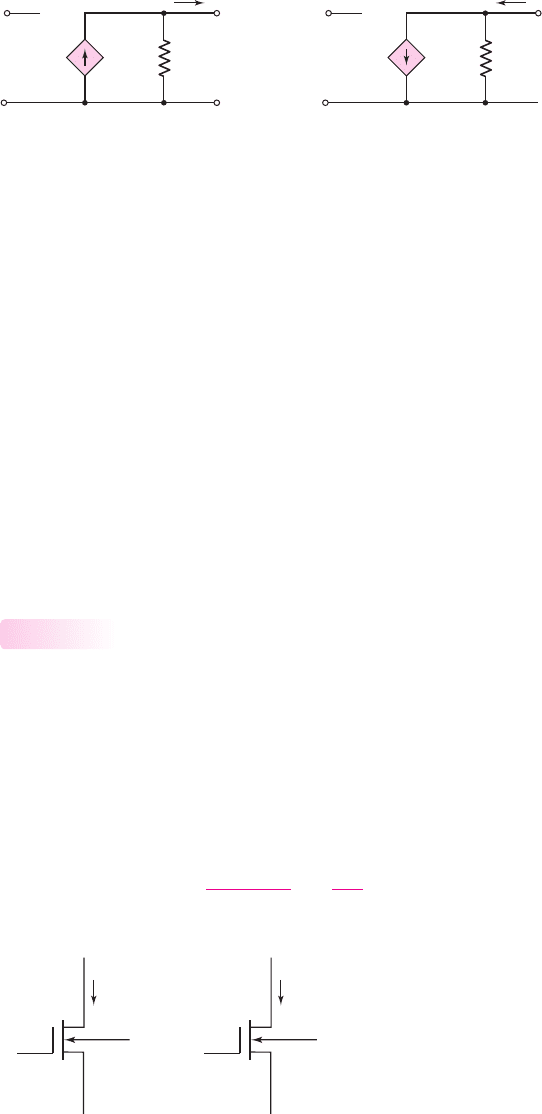
214 Part 1 Semiconductor Devices and Basic Applications

This expression for the small-signal voltage gain of the p-channel MOSFET

ampliﬁer is exactly the same as that for the n-channel MOSFET ampliﬁer. The

negative sign indicates that a 180-degree phase reversal exists between the ouput and

input signals, for both the PMOS and the NMOS circuit.

We may note that if the polarity of the small-signal gate-to-source voltage is

reversed, then the small-signal drain current direction is reversed. This change of po-

larity is shown in Figure 4.11. Figure 4.11(a) shows the conventional voltage polar-

ity and current directions in a PMOS transistor. If the control voltage polarity is re-

versed as shown in Figure 4.11(b), then the dependent current direction is also

reversed. The equivalent circuit shown in Figure 4.11(b) is then the same as that of

the NMOS transistor. However, the author prefers to use the small-signal equivalent

circuit in Figure 4.9 to be consistent with the voltage polarities and current directions

of the PMOS transistor.

Modeling the Body Effect

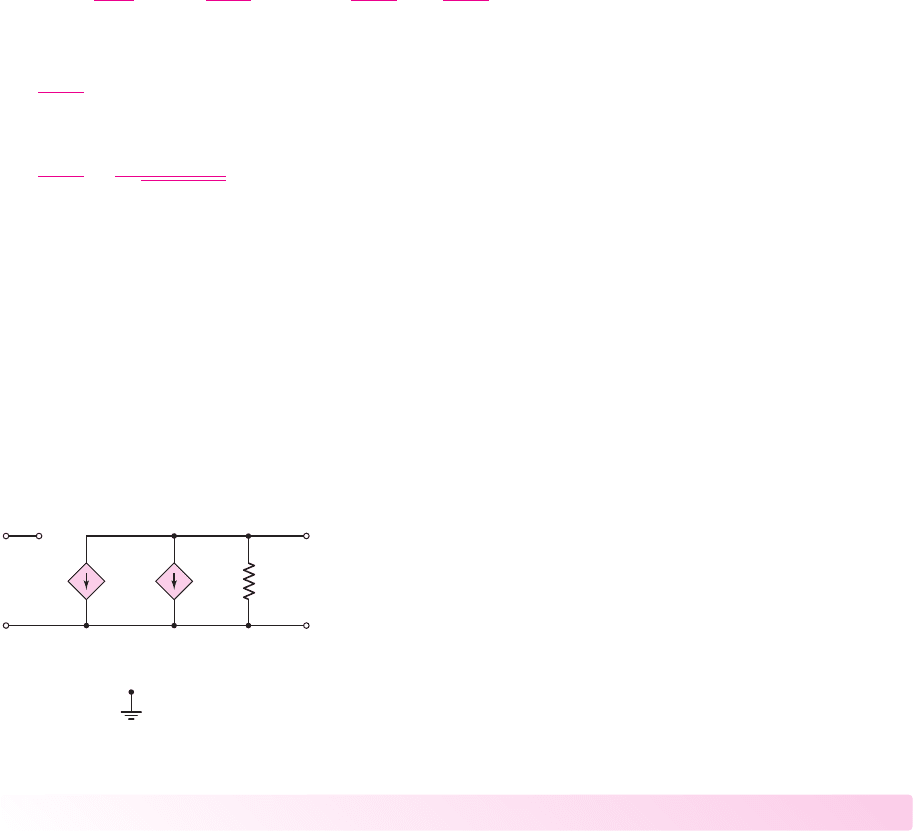
As mentioned in Section 3.1.9, Chapter 3, the body effect occurs in a MOSFET in

which the substrate, or body, is not directly connected to the source. For an NMOS

device, the body is connected to the most negative potential in the circuit and will be

at signal ground. Figure 4.12(a) shows the four-terminal MOSFET with dc voltages

and Figure 4.12(b) shows the device with ac voltages. Keep in mind that v

must be

greater than or equal to zero. The simpliﬁed current-voltage relation is

= K

− V

)

(4.22)

and the threshold voltage is given by

= V

TNO

+γ





2φ

−



2φ



(4.23)

4.1.3

–

(a) (b)

Figure 4.11 Small signal equivalent circuit of a p-channel MOSFET showing (a) the

conventional voltage polarities and current directions and (b) the case when the voltage

polarities and current directions are reversed.

–

–+

––

(a) (b)

Figure 4.12 The four-terminal NMOS device with (a) dc voltages and (b) ac voltages

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 214 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

Chapter 4 Basic FET Ampliﬁers 215

If an ac component exists in the source-to-body voltage, v

, there will be an ac

component induced in the threshold voltage, which causes an ac component in the

drain current. Thus, a back-gate transconductance can be deﬁned as

∂i

∂v



Q-pt

−∂i

∂v



Q-pt

=−



∂i

∂V





∂V

∂v





Q-pt

(4.24)

Using Equation (4.22), we ﬁnd

∂i

∂V

=−2K

− V

) =−g

(4.25(a))

and using Equation (4.23), we ﬁnd

∂V

∂v



2φ

≡ η

(4.25(b))

The back-gate transconductance is then

=−(−g

) · (η) = g

(4.26)

Including the body effect, the small-signal equivalent circuit of the MOSFET is

shown in Figure 4.13. We note the direction of the current and the polarity of the

small-signal source-to-body voltage. If

> 0

, then

decreases,

and i

increases. The current direction and voltage polarity are thus consistent.

For

= 0.35

V and

γ = 0.35 V

1/2

, the value of

from Equation (4.25(b)) is

∼

0.23

. Therefore,

will be in the range

0 ≤ η ≤ 0.23

. The value of v

will

depend on the particular circuit.

In general, we will neglect g

in our hand analyses and designs, but will inves-

tigate the body effect in PSpice analyses.

–

Figure 4.13 Small-signal equivalent circuit of NMOS device including body effect

Test Your Understanding

TYU 4.1 The parameters of an n-channel MOSFET are:

= 0.6



100 μ

A/V

, and

λ = 0.015

−1

. The transistor is biased in the saturation region with

= 1.2

mA. (a) Design the width-to-length ratio such that the transconductance is

= 2.5

mA/V. (b) Determine the small-signal output resistance

. (Ans. (a) 26.0,

(b) 55.6 k

)

TYU 4.2 For the circuit shown in Figure 4.1,

= 3.3

V and

= 8



The transistor parameters are

= 0.4

= 0.5

mA/V

, and

λ = 0.02

−1

(a) Determine

GSQ

and

DSQ

for

= 0.15

mA. (b) Calculate

, and the small-

signal voltage gain. (Ans. (a)

GSQ

= 0.948

DSQ

= 2.1

V; (b)

= 0.548

mA/V,

= 333



=−4.28)

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 215 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

216 Part 1 Semiconductor Devices and Basic Applications

TYU 4.3 For the circuit in Figure 4.1, the circuit and transistor parameters are given

in Exercise TYU 4.2. If

= 25 sin ωt

(mV), determine

and

. (Ans.

= 0.15 +0.0137 sin ωt

(mA),

= 2.1 −0.11 sin ωt

(V)).

TYU 4.4 The parameters for the circuit in Figure 4.8 are

= 5

V and

= 5



The transistor parameters are

=−0.4

= 0.4

mA/V

, and

λ = 0

. (a) De-

termine

SGQ

and

such that

SDQ

= 3

V. (b) Calculate

and the small-signal

voltage gain. (Ans. (a)

= 0.4

mA,

SGQ

= 1.4

V; (b)

= 0.8

mA/V,

=−4)

TYU 4.5 A transistor has the same parameters as those given in Exercise Ex4.1. In

addition, the body effect coefﬁcient is

γ = 0.40

1/2

and

= 0.35

V. Determine

the value of

and the back-gate transconductance g

for (a)

= 1

V and

(b)

= 3

V. (Ans. (a)

η = 0.153

, (b)

η = 0.104)

4.2 BASIC TRANSISTOR AMPLIFIER

CONFIGURATIONS

Objective: • Discuss the three basic transistor ampliﬁer conﬁgurations.

As we have seen, the MOSFET is a three-terminal device. Three basic single-

transistor ampliﬁer conﬁgurations can be formed, depending on which of the three

transistor terminals is used as signal ground. These three basic conﬁgurations are

appropriately called common source, common drain (source follower), and

common gate.

The input and output resistance characteristics of ampliﬁers are important in

determining loading effects. These parameters, as well as voltage gain, for the three

basic MOSFET circuit conﬁgurations will be determined in the following sections.

The characteristics of the three types of ampliﬁers will then allow us to understand

under what condition each ampliﬁer is most useful.

Initially, we will consider MOSFET ampliﬁer circuits that emphasize discrete

designs, in that resistor biasing will be used. The purpose is to become familiar

with basic MOSFET ampliﬁer designs and their characteristics. In Section 4.7, we

will begin to consider integrated circuit MOSFET designs that involve all-transis-

tor circuits and current source biasing. These initial designs provide an introduc-

tion to more advanced MOS ampliﬁer designs that will be considered in Part 2 of

the text.

4.3 THE COMMON-SOURCE AMPLIFIER

Objective: • Analyze the common-source ampliﬁer and become

familiar with the general characteristics of this circuit.

In this section, we consider the ﬁrst of the three basic circuits—the common-source

ampliﬁer. We will analyze several basic common-source circuits, and will determine

small-signal voltage gain and input and output impedances.

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 216 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04:

Chapter 4 Basic FET Ampliﬁers 217

A Basic Common-Source Conﬁguration

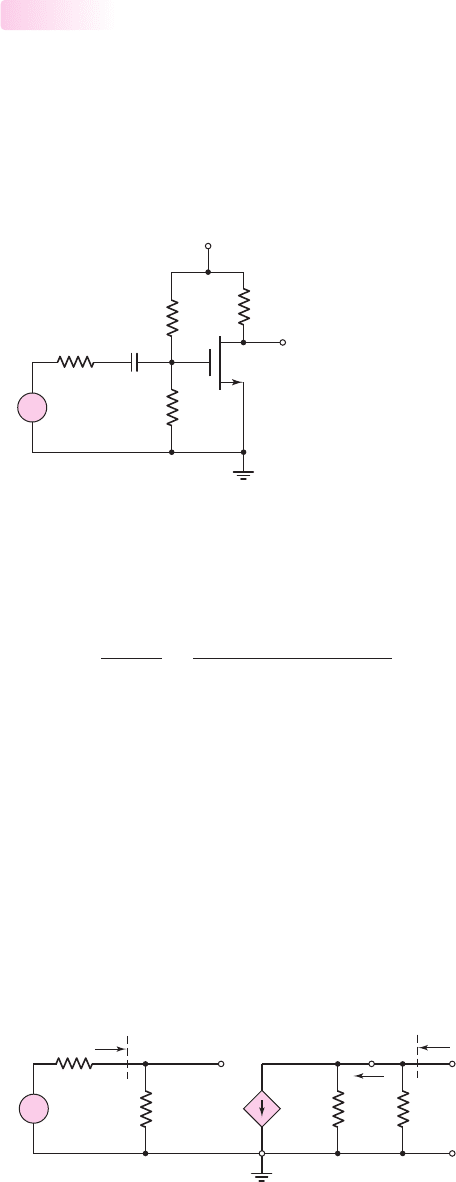
Figure 4.14 shows the basic common-source circuit with voltage-divider biasing. We

see that the source is at ground potential—hence the name common source. The sig-

nal from the signal source is coupled into the gate of the transistor through the cou-

pling capacitor C

, which provides dc isolation between the ampliﬁer and the signal

source. The dc transistor biasing is established by R

and R

, and is not disturbed

when the signal source is capacitively coupled to the ampliﬁer.

4.3.1

–

Figure 4.14 Common-source circuit with voltage divider biasing and coupling capacitor

–

⎜⎜ R

–

Figure 4.15 Small-signal equivalent circuit, assuming coupling capacitor acts as a short circuit

If the signal source is a sinusoidal voltage at frequency f, then the magnitude

of the capacitor impedance is

[

1/(2π fC

)

]

. For example, assume that

= 10 μ

F and

f = 2

kHz. The magnitude of the capacitor impedance is then

2π fC

2π(2 ×10

)(10 × 10

−6

)

∼

8 

The magnitude of this impedance is generally much less than the Thevenin resistance

at the capacitor terminals. We can therefore assume that the capacitor is essentially a

short circuit to signals with frequencies greater than 2 kHz. We will also neglect, in

this chapter, any capacitance effects within the transistor.

For the circuit shown in Figure 4.14, assume that the transistor is biased in the sat-

uration region by resistors R

and R

, and that the signal frequency is sufﬁciently large

for the coupling capacitor to act essentially as a short circuit. The signal source is rep-

resented by a Thevenin equivalent circuit, in which the signal voltage source v

is in

series with an equivalent source resistance R

. As we will see, R

should be much less

than the ampliﬁer input resistance,

= R

R

, in order to minimize loading effects.

Figure 4.15 shows the resulting small-signal equivalent circuit. The small-

signal variables, such as the input signal voltage V

, are given in phasor form.

nea80644_ch04_205-284.qxd 06/12/2009 08:00 PM Page 217 F506 Tempwork:Dont' Del Rakesh:June:Rakesh 06-12-09:MHDQ134-04: