Салимов Р.Б. Математика (для студентов бакалавриата)
Подождите немного. Документ загружается.


21
поскольку вектор
a
ортогонален и
1
,
b
и
1
.
c
Кроме того,
11
| | | || |.d ab c= +
Заметим,
что
1 2 11
( , ) ( , ),dd bc=
так как вектор
1
d
ортогонален
1
,
b
а вектор
2
d
ортогонален
1
.
c
Но
d
ортогонален
11
,bc+
поэтому угол
1
(,)dd
равен углу между векторами
1
b
и
11
.bc+
Таким образом, векторы
12
,,ddd
получаются поворотом вокруг
a
соот-
ветственно векторов
11
,bc+
1
,b
1
c
на угол, равный
/ 2,
π
в одном и том же
направлении (против хода часовой стрелки, если смотреть с конца вектора
a
)
и умножением их на
||a
. Это означает, что
12
.ddd= +
Учитывая, что
0011
,bcb c b c+= + + +
где
00
bc+
– вектор, коллинеарный
a
,
11
bc+
ортогонален
a
, и
приняв во внимание предыдущие соотношения, имеем
0011 11 1 1
()( )()abc abcbc abc abac×+=×+++=×+=×+×=
,abac=×+×
что и требовалось.
Пусть векторы и заданы своими проекциями: =( , , ),
. Тогда = + + , = + + . Сначала рассмотрим
векторные произведения базисных векторов.
С помощью определения векторного произведения покажем справедли-
вость равенств
;ijk×=
;jk i×=
;ki j×=
;ji k×=−
;kj i×=−
;ik j×=−
(19)
0;ii×=
0;jj×=
0.kk×=
(20)
Итак, пусть
.ijc×=
Вектор обладает свойствами:
• = 1⋅1⋅1 = 1;
• , , т. е. перпендикулярен к плоскости, в которой лежат век-
торы и ;
• направлен так, что если смотреть с его конца, то кратчайший поворот
от первого вектора ко второму вектору совершается против хода часовой
стрелки, т. е. совпадает с , следовательно,
.ijk×=
Покажем, что
0.ii×=
Пусть
.ii c×=
Тогда =0,
=0, т. е.
0.ii×=
Аналогично доказываются остальные равенства (19) и (20).
Рассмотрим векторное произведение
a
b
a
x
a
y
a
z
a
(, , )
xyz
b bbb=
a
x
a
i
y
a
j
z
a
k
b
x
b
i
y
b
j
z
b
k
c
( )
sin ,c ij ij=
ci⊥
cj⊥
c
i
j
c
i
j
c
k
( )
sin ,c ii ii=
c

5354.ru
22
( ) ( ).
xy z xy z
a b ai a j ak bi b j bk×= + + × + +
Использовав последние два свойства, запишем
[] [] [] [] [ ]
xx xy xz yx yy
a b ab i i ab i j ab i k ab j i ab j j×= ×+ × + × + ×+ × +
[] [] [] [].
yz zx zy zz
ab j k ab k i ab k j ab k k+ × + ×+ × + ×
Отсюда с учётом (19) и (20) имеем
×
= + + - .
Итак,
×
=( - ) -( - ) +( - ) . (21)
Следовательно (см. § 1),
.
yz xy
xz
yz xy
xz
aa aa
aa
ab i j k
bb bb
bb
×= − +
. (22)
Эту формулу можно записать так:
.
xyz
xyz
i jk
ab a a a
bbb
×=
(23)
Таким образом, если и заданы своими проекциями, то векторное про-
изведение двух векторов определяется по формуле (23).
Условие коллинеарности двух векторов. Если для ненулевых векторов
выполняется условие
0,ab
× =
то
a
и
b
коллинеарны. В самом деле, если
0,ab× =
то
sin 0a b ab
ϕ
×= =
и , т. е. или . Следовательно,
векторы , коллинеарны.
В этом случае из (21) имеем - =0, - =0, - =0. Зна-
чит,
/ / /.
xx yy zz
ab ab ab= =
Это и есть условие коллине-арности двух векторов,
заданных своими проекциями.
Решим следующую задачу: определить площадь треугольника, заданного
своими вершинами.
Пусть , , – вершины треугольника в про-
странстве , а их координаты – заданные числа. Найдем векторы (см. § 7)
2 1 2 12 1
( , , ),AB x x y y z z=−−−
3 1 3 13 1
( , , ),AC x x y y z z=−−−
a
b
x
a
y
b
k
−
x
a
z
b
j
−
y
a
x
b
k
y
a
z
b
i
z
a
x
b
j
z
a
y
b
i
a
b
y
a
z
b
z
a
y
b
i
x
a
z
b
z
a
x
b
j
x
a
y
b
y
a
x
b
k
a
b
sin 0
ϕ
=
0
ϕ
=
ϕπ
=
a
b
y
a
z
b
z
a
y
b
x
a
z
b
z
a
x
b
x
a
y
b
y
a
x
b
1 11
(,,)Ax y z
2 22
(,,)Bx y z
3 33
(,,)Cx y z
Oxyz

23
векторное произведение которых обозначим
xyz
d di d j dk=++
=
.AB AC×
Тогда
согласно (22)
и Площадь параллелограмма, построенного на векторах
AB
и
,AC
равна найденному числу , поэтому искомая площадь треугольника
определяется по формуле .
§ 11. Смешанное произведение векторов и его геометрический
смысл.
Условие компланарности трех векторов
Даны векторы , и . Векторы , перемножим векторно и получим
.d ab= ×
Этот вектор умножим скалярно на и получим число , которое
называется смешанным (векторно-скалярным) произведением трёх исходных
векторов , , и обозначается
( , , ) = =
( )
,.abc
×
(24)
Рассмотрим это смешанное произведение, когда векторы заданы своими про-
екциями , , . Проекции вектора на
оси координат определяются по формуле (22).
Скалярное произведение векторов и равно сумме произведений одно-
имённых проекций:
.
Левая часть этой формулы – смешанное произведение ( , , ). Правую часть
запишем в виде определителя третьего порядка:
. (25)
Эта формула позволяет вычислить смешанное произведение векторов, за-
данных своими проекциями. Выясним теперь
2 12 1
3 13 1
,
x
y yz z
d
y yz z
−−
=
−−
2 12 1
3 13 1
,
y
x xz z
d
x xz z
−−
= −
−−
2 12 1
3 13 1
z
x xy y
d
x xy y
−−
=
−−
222
|| .
xyz
d ddd= ++
||
d
| |/2Sd
∆
=
a
b
c
a
b
c
( )
,dc
a
b
c
a
b
c
( )
,dc
(, , )
xyz
a aaa=
(, , )
xyz
b bbb=
(, , )
xyz
c ccc=
d
d
c
(,)
yz xy
xz
xyz
yz xz xy
aa aa
aa
dc c c c
bb bb bb
=−+
a
b
c
( )
,,
xyz
xyz
xyz
aaa
abc b b b
ccc
=
5354.ru
24
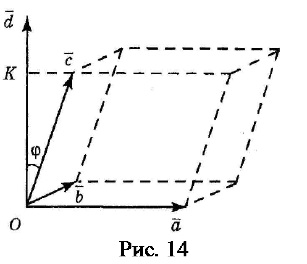
Геометрический смысл смешанного произведения. Даны векторы ,
и . Построим эти векторы, поместив их начала в общей точке, а затем на них
как на рёбрах построим параллелепипед (рис. 14). Построим вектор
d ab= ×
,
перпендикулярный к плоскости, в которой лежат векторы и , т. е. перпен-
дикулярный к нижнему основанию параллелепипеда. Длина | | равна площа-
ди
S
нижнего основания параллелепипеда (т. е. площади параллелограмма,
построенного на векторах и как на сторонах). Через конец проведём
плоскость, перпендикулярную к (ясно, что верхнее основание параллеле-
пипеда лежит в этой плоскости). Эта плоскость пере-
сечёт вектор (или его продолжение) в точке К (К –
проекция конца вектора на указанную линию). Из
построения следует, что расстояние ОК равно высоте
параллелепипеда. Пусть – угол между и . На
рис. 14 изображен случай, когда
/2,
ϕπ
<
при этом
Смешанное произведение
Но и Поэтому где
– объём параллелепипеда. Этот результат мы получили для случая, когда
. Если , то вектор лежит ниже плоскости векторов , , при
этом и Итак, справедлива формула
(26)
где – объем параллелепипеда.
Определение. Три вектора называются компланарными, если они лежат в
одной плоскости.
Условие компланарности трех векторов. Если для трёх ненулевых век-
торов , и выполняется условие
(,,) 0abc =
, (27)
то эти векторы компланарны.
Действительно, в этом случае согласно (26) имеем
(,,)abc =
0.V Sh=±=± =
Отсюда следует, что три вектора лежат в одной плоскости, так как или
0,S =
или
0.h =
Если , и заданы своими проекциями, то условие компланарности
(27) с учётом (25) можно записать так:
a
b
c
a
b
d
a
b
c
d
d
c
h
ϕ
d
c
| |cos .OK h c
ϕ
= =
(,,) (,) | || |cos.abc dc d c
ϕ
= =
||dS=
| |cos .hc
ϕ
=
(,,) ,a b c Sh V= =
V
ϕπ
< /2
ϕπ
> /2
c
a
b
| |cosOK h c
ϕ
= = −
(,,) .a b c Sh V=−=−
(,,) ,abc V= ±
V
a
b
c
a
b
c

25
.
Это условие проверяется непосредственно по заданным проекциям рас-
сматриваемых векторов.
0
xyz
xyz
xyz
aaa
bbb
ccc
=

5354.ru
26
ГЛАВА 2. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
§ 1. Уравнение поверхности и уравнения линии в пространстве
В аналитической геометрии любую поверхность в
пространстве рассматривают как геометрическое место
точек, обладающих определённым свойством. Распо-
ложим указанную поверхность в системе координат
Oxyz. Свойство, общее для всех точек поверхности, за-
пишем аналитически, т. е. в виде соотношения, связы-
вающего координаты
,,xyz
произвольной точки
M
поверхности:
, (1)
где левая часть – известное выражение, содержащее . Фор-
мула (1) называется уравнением поверхности в пространстве Oxyz, а величи-
ны – текущими координатами. Например, сфера радиуса R с центром
(0, 0, 0) (см. рис. 15) определяется уравнением
. (2)
В самом деле, для любой точки М( ) сферы расстояние ОМ=R. Заметив,
что подставим это выражение в предыдущую
формулу, возведем в квадрат и перенесем влево, при этом получим (2).
Поэтому (2) является уравнением сферы.
По построению уравнению (1) удовлетворяют координаты любой точки
поверхности и не удовлетворяют координаты точек, не лежащих на поверх-
ности. Можно сформулировать и обратное утверждение: каждому уравнению
вида (1) в пространстве Oxyz отвечает некоторая поверхность – геометриче-
ское место точек, координаты которых удовлетворяют (1), если не имеет ме-
сто случай, когда это уравнение не определяет никакого множества точек,
например, , или когда уравнение определяет одну точку,
например, .
Итак, каждой поверхности в пространстве Oxyz отвечает уравнение вида
(1). Это обстоятельство позволяет свести изучение геометрических свойств
( )
,, 0Fx y z=
( )
,,Fx y z
,,xyz
,,xyz
222 2
0xyzR++− =
,,xyz
( ) ( ) ( )
2 22
0 0 0,OM x y z= −+−+−
2
R
222
10xyz+ + +=
222
0xyz++=

27
поверхностей к изучению их уравнений аналитическими методами. Этим и
занимается аналитическая геометрия.
Уравнения линии в пространстве. Линию в пространстве Oxyz будем
рассматривать как линию пересечения двух поверхностей. Пусть каждая из
этих поверхностей определяется одним из уравнений
1
2
( , , ) 0,
( , , ) 0.
F xyz
F xyz
=
=
(3)
Тогда координаты любой точки линии удовлетворяют каждому
из этих уравнений, так как эта точка лежит на обеих поверхностях. Таким об-
разом, линии отвечает система двух уравнений (3). Эта система называется
уравнениями линии в пространстве.
Итак, линии в пространстве отвечает система уравнений (3) и, наобо-
рот, каждой системе уравнений (3) в пространстве Oxyz отвечает некоторая
линия – геометрическое место точек, координаты которых удовлетворяют
этой системе.
§ 2. Плоскость, общее уравнение плоскости
Пусть в пространстве Oxyz задана плоскость, т. е. заданы:
• координаты точки , лежащей на этой плоскости;
• – проекции на оси координат ненулевого вектора ,
перпендикулярного плоскости, который называется нормальным вектором
плоскости.
Пусть – произвольная точка плоскости. Рассмотрим вектор
(см. рис. 16). Он лежит на рассматриваемой плоско-
сти и поэтому перпендикулярен нормальному вектору этой плоскости,
следовательно, скалярное произведение этих векто-
ров . Выразим скалярное произведение
через проекции векторов. Получим
. (4)
Это есть уравнение рассматриваемой плоскости,
Здесь
,,xyz
– текущие координаты, т. е. координа-
ты произвольной точки плоскости.
L
,,xyz
M
L
L
L
L
000
,,xyz
0
M
,,ABC
( )
,,N ABC=
( )
,,Mxyz
( )
0 0 00
,,MM x x y y z z=−−−
N
( )
0
,0MMN =
( ) ( ) ( )
0 00
0Ax x By y Cz z−+ −+ −=
5354.ru
28
Общее уравнение плоскости. Возьмём уравнение первой степени отно-
сительно
,,xyz
:
, (5)
где A, B, C, D – заданные числа. Будем считать, что A, B, C одновременно не
обращаются в нуль. Если же эти числа обращаются в нуль одновременно, то
(5) примет вид и уже не будет уравнением. Пусть , тогда (5) можно
записать в виде
. (6)
Но это есть уравнение вида (4), поэтому оно (следовательно, и уравнение (5))
определяет в пространстве Oxyz плоскость, проходящую через точку
и перпендикулярную к вектору .
Итак, уравнение (5) в пространстве всегда определяет плоскость с нор-
мальным вектором . Оно называется общим уравнением плоско-
сти. Мы показали также, что в (5) числа (коэффициенты уравнения
при текущих координатах) представляют собой проекции на оси координат
нормального вектора этой плоскости. Отметим отдельные частные случаи
уравнения (5).
Пусть в (5) , тогда уравнение примет вид , плоскость в
этом случае проходит через точку , так как координаты точки О удо-
влетворяют этому уравнению.
Пусть , тогда получим уравнение . В этом случае плос-
кость параллельна оси Oz, так как её нормальный вектор перпен-
дикулярен к оси Oz. В самом деле, здесь проекция вектора на ось Oz равна
. Следовательно, , значит, угол .
Пусть , . Тогда имеем уравнение . Плоскость проходит
через ось Oz, так как проходит через начало координат О (поскольку ),
кроме того, она параллельна оси Oz (поскольку ).
Пусть , . Тогда или . Плоскость параллельна
плоскости
Oyz
, так как она параллельна оси Oz (поскольку ) и парал-
лельна оси Oy (поскольку ).
Пусть , , . Тогда или . Это уравнение определя-
ет плоскость
Oyz
, так как плоскость параллельна
Oyz
, как и в предыдущем
0Ax By C z D+ + +=
0D =
0C ≠
( ) ( ) ( )
0 0 ( /) 0Ax By Cz DC−+ −+ −− =
( )
0
0,0, /M DC−
( )
,,N ABC=
( )
,,N ABC=
,,ABC
N
0D =
0Ax By Cz++=
( )
0,0,0O
0C =
0Ax By D+ +=
( )
, ,0N AB=
N
( )
cos , 0N Oz N =
( )
cos , 0Oz N =
( )
, /2Oz N
π
=
0D =
0C =
0Ax By+=
0D =
0C =
0B =
0C =
0Ax D+=
/x DA= −
0C =
0B =
0B =
0C =
0D =
0Ax =
0x =
29
случае, кроме того, она проходит через точку О (поскольку ). Остальные
случаи рассматриваются по аналогии.
§ 3. Угол между двумя плоскостями,
условия параллельности и перпендикулярности плоскостей
Пусть в пространстве Oxyz заданы две плоскости соответственно уравне-
ниями
, (7)
, (8)
где коэффициенты
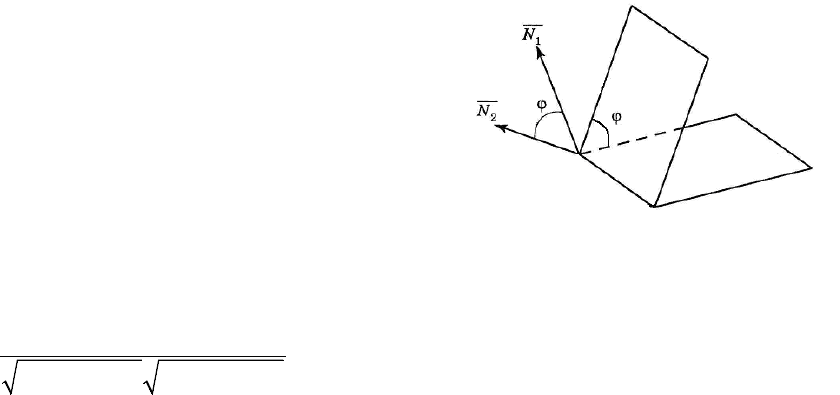
– заданные числа. Тогда векторы и
– нормальные векторы этих плос-
костей (см. рис. 17). За угол между плоско-
стями (7) и (8) примем один из двухгранных уг-
лов (образованных ими), равный углу между их
нормальными векторами. Использовав формулу
(18) главы 1, определим
. (9)
Вычислив по формуле (9) , найдём угол .
Если , то плоскости (7), (8) параллельны между собой, так
как коллинеарны их нормальные векторы.
Если , то плоскости (7), (8) перпендикулярны между со-
бой, так как перпендику-лярны их нормальные векторы.
§ 4. Расстояние от точки до плоскости в пространстве
Пусть в пространстве Oxyz плоскость задана уравнением
,. (10)
где A, B, C, D – известные числа. Дана точка , ее координаты
– заданные числа. Нужно найти d – расстояние от точки до плос-
0D =
1111
0Ax By Cz D+ + +=
2222
0Ax By Cz D+ + +=
1
,A
1
,B
1
,C
1
,D
2
,A
2
,B
2
,C
2
D
( )
1 111
,,N ABC=
( )
2 222
,,N ABC=
ϕ
12 12 12
222222
111222
cos
AA BB CC
ABCABC
ϕ
++
=
++ ++
cos
ϕ
ϕ
12 12 12
///AABBCC= =
12 12 12
0AA BB CC++=
0Ax By Cz D+ + +=
( )
1 111
,,M xyz
1 11
,,xyz
1
M
Рис. 17

5354.ru
30
кости с уравнением (10). Нормальный вектор этой плоскости равен
Пусть – основание перпендикуляра, опущенного из точки
на заданную плоскость (рис. 18). Ясно, что
длина вектора равна искомому расстоя-
нию d. Ясно также, что вектор коллине-
арен . Проекции вектора на оси коор-
динат равны разностям координат конца и
начала:
Скалярное произ-
ведение этого вектора и вектора определим
по формуле (17) главы 1:
. (11)
С другой стороны, скалярное произведение в левой части (11) равно
. (12)
Здесь
1+
берётся, когда угол , и
1−
, когда этот угол равен
.
π
Вы-
ражение (12) подставим в левую часть формулы (11), а в правой части рас-
кроем скобки. Получим
. (13)
Точка лежит на плоскости с уравнением (10), поэтому её координаты
удовлетворяют (10), т. е. имеет место соотношение
. Значит, Теперь формулу (13) можно
записать так: . Найдем теперь
d
, учитывая, что
:
. (14)
Из формулы (14) видно, что для нахождения расстояния
d
от точки до
плоскости с уравнением (10) нужно в левую часть уравнения (10) вместо
поставить координаты заданной точки , а затем найденное
( )
,, .N ABC=
( )
0 000
,,M xyz
1
M
01
MM
01
MM
N
01
MM
( )
0 1 1 0 1 01 0
,, .MM x x y y z z=−−−
N
( )
( ) ( ) ( )
01 1 0 1 0 1 0
,MM N Ax x B y y C z z= −+ −+ −
( )
( )
( )
01 01 01
, cos , 1MM N MM N MM N dN= = ±
( )
01
,0MM N =
( )
111 0 00
1d N Ax By Cz Ax By Cz±= + + − − −
0
M
000
,,xyz
000
0Ax By Cz D+ + +=
000
.Ax By Cz D−−−=
( )
111
1d N Ax By Cz D±= + + +
222
N ABC= ++
( )
111
222
1
Ax By Cz D
d
ABC
+++
±=
++
1
M
,,xyz
111
,,xyz
1
M
