Салимов Р.Б. Математика (для студентов бакалавриата)
Подождите немного. Документ загружается.

51
плоскости получаем эллипс наибольших размеров. При значения
и достигают наименьших значений и Это означает, что плоско-
сти и имеют с эллипсоидом по одной общей точке и
соответственно. При эллипсоид с плоскостью общих точек не
имеет. Аналогичная картина будет при сечении эллипсоида плоскостью
( ) и плоскостью ( ) (рис. 34).
При имеем эллипсоид вращения, поскольку в плоскости
zh=
вместо
эллипса получаем окружность. Эта поверхность получается при вращении
вокруг оси эллипса
22
22
1,
xz
ac
+=
расположенного в плоскости
§ 20. Конус
Конусом второго порядка называется поверхность, определяемая уравне-
нием
2 22
222
0.
xyz
abc
+−=
(59)
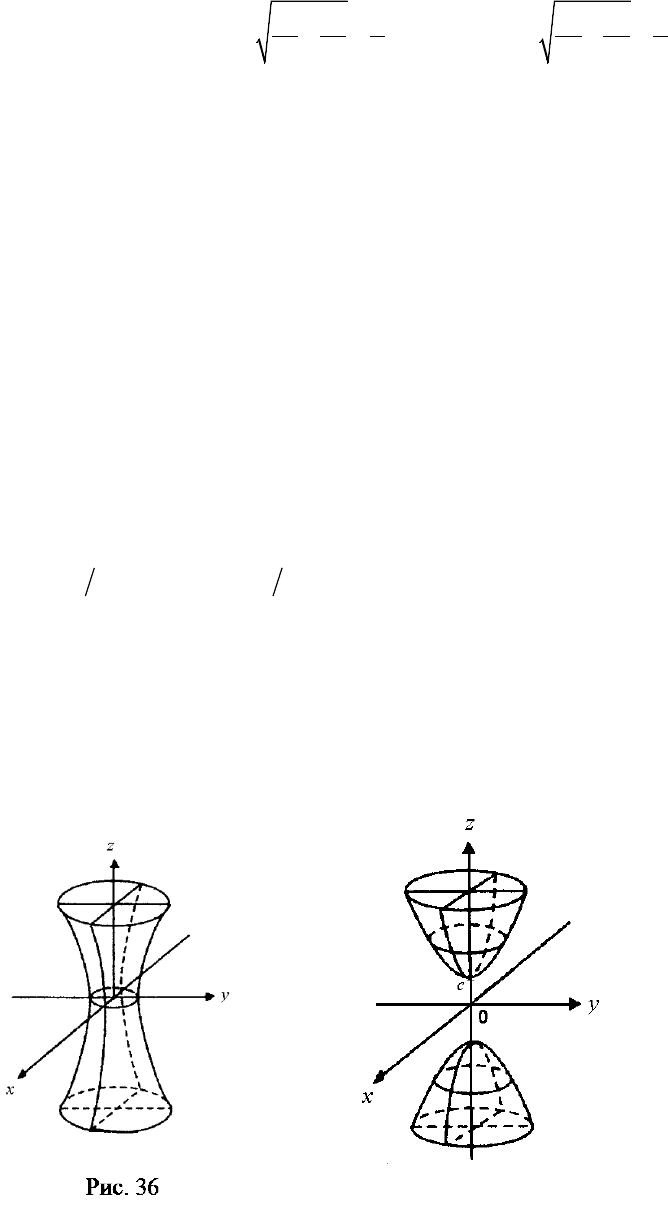
где – заданные положительные числа (см. рис. 35). Исследовав форму
этой поверхности, как и эллипсоида, методом сечений, получим, что при се-
чении плоскостью ( – постоянная) получается эллипс с полуосями
и Очевидно, что при т. е. конус (59) имеет
с плоскостью одну общую точку – начало координат. С увеличением
значения и увеличиваются. Покажем теперь, что
при сечении поверхности (59) плоскостью с уравнением
( – постоянная), проходящей через получа-
ется пара прямых, проходящих через начало координат.
В самом деле, при таком сечении получается линия,
определяемая системой уравнений
22 22 22
/ / / 0,
.
xa yb zc
y kx
+−=
=
Заменим в первом уравнении на получим
22 22 22
/ ( ) / / 0,
.
x a kx b z c
y kx
+ −=
=
Но первое уравнение равносильно совокупности двух уравнений
и
Oxy
||hc=
1
a
1
b
1
0a =
1
0.b =
zc=
zc= −
(0,0, )c
(0,0, )c−
||hc>
zh=
1
xh=
1
ah a−≤ ≤
2
yh=
2
bh b−≤ ≤
ab=
Oz
.Oxz
,,abc
zh=
h
1
||a ah c=
1
||.b bh c=
0h =
11
0,ab= =
Oxy
||h
1
a
1
b
y kx=
k
,Oz
y
,kx
2
22
1 kz
x
ab c
+=
2
22
1
.
kz
x
ab c
+=−
5354.ru
52
Поэтому последняя система равносильна совокупности двух систем
и
Все уравнения в этих системах определяют плоскости, проходящие через
начало координат. Значит, каждая система определяет в пространстве пря-
мую, проходящую через начало координат. При получаем конус враще-
ния (вокруг оси ).
§ 21. Однополостный и двуполостный гиперболоиды
Однополостный гиперболоид – это поверхность, определяемая уравнени-
ем
22 22 22
/ / / 1,xa yb zc
+−=
(60)
где – заданные положительные числа. Исследуем форму этой поверх-
ности. В сечении ее плоскостью получается эллипс с полуосями
и С увеличением эти полуоси увеличиваются. В
сечениях поверхности (60) плоскостью (с уравнением ) и плоскостью
( ) получаются гиперболы
22 22
/ /1yb zc−=
и
22 22
/ /1xa zc−=
соответственно. Поверхность имеет вид, указанный на рис. 36. При по-
лучаем однополостный гиперболоид вращения ( – ось вращения).
На рассматриваемой поверхности лежат семейства прямых, которые
называются прямолинейными образующими. В частности, система уравнений
1
/ / (1 / ),
/ / (1 / ),
xa zc k yb
xa zc k yb
−
+=+
−= −
(61)
2
22
1
0,
kz
x
abc
y kx
+ −=
=
2
22
1
0,
.
kz
x
abc
y kx
+ +=
=
ab=
Oz
,,a bc
zh=
2 2 1/2
(1 ( ))a hc+
2 2 1/2
(1 ( )) .b hc+
h
Oyz
0x =
Oxz
0y =
ab=
Oz
Рис. 37
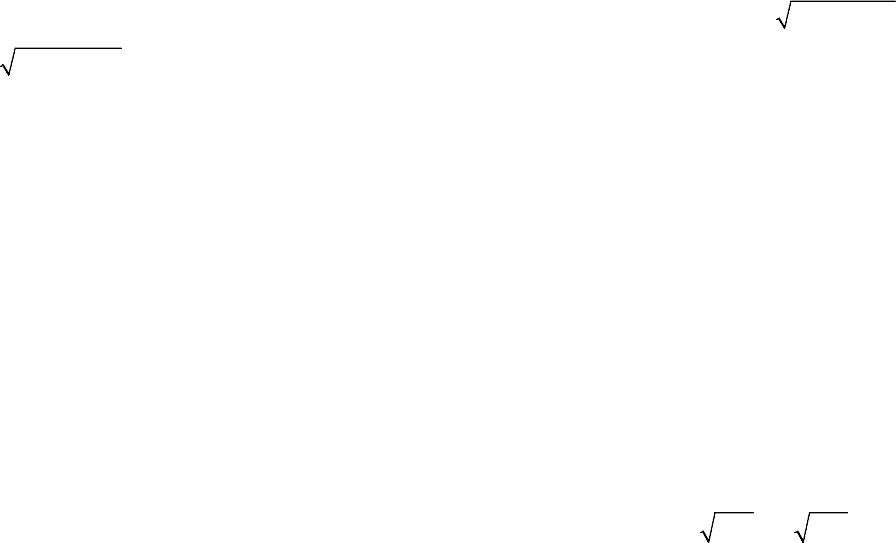
53
где – произвольное заданное число, в пространстве определяет пря-
мую. Перемножив почленно уравнения системы, перейдём к уравнению (60).
Следовательно, координаты любой точки этой прямой удовлетво-
ряют уравнению (60), т. е. точка принадлежит поверхности (60). Таким
образом, прямая (61) лежит на поверхности. Изменяя значение величины в
системе (61), получим семейство прямолинейных образующих однополостно-
го гиперболоида (60). Другое семейство прямолинейных образующих этого
гиперболоида определяется системой
1
/ / (1 / ),
/ / (1 / ),
xa zc l yb
xa zc l yb
−
+=−
−= +
где – произвольное число.
Двуполостный гиперболоид – это поверхность, определяемая уравнением
22 22 22
/ / / 1,xa yb zc+−=−
(62)
где – заданные положительные числа. Рассекая поверхность (62)
плоскостью ( ), в сечении получим эллипс с полуосями
22
1/a hc−+
и
22
1/b hc−+
(см. рис. 37). При плоскость и поверхность не пересека-
ются.
В сечениях поверхности (62) плоскостью ( ) и плоскостью (
) будем иметь гиперболы
22 22
/ /1zc yb−=
и
22 22
/ /1zc xa−=
соответствен-
но. При получим двуполостный гиперболоид вращения ( – ось враще-
ния).
§ 22. Эллиптический и гиперболический параболоиды
Эллиптический параболоид – это поверхность, определяемая уравнением
22
/ / 2,xpyq z+=
(63)
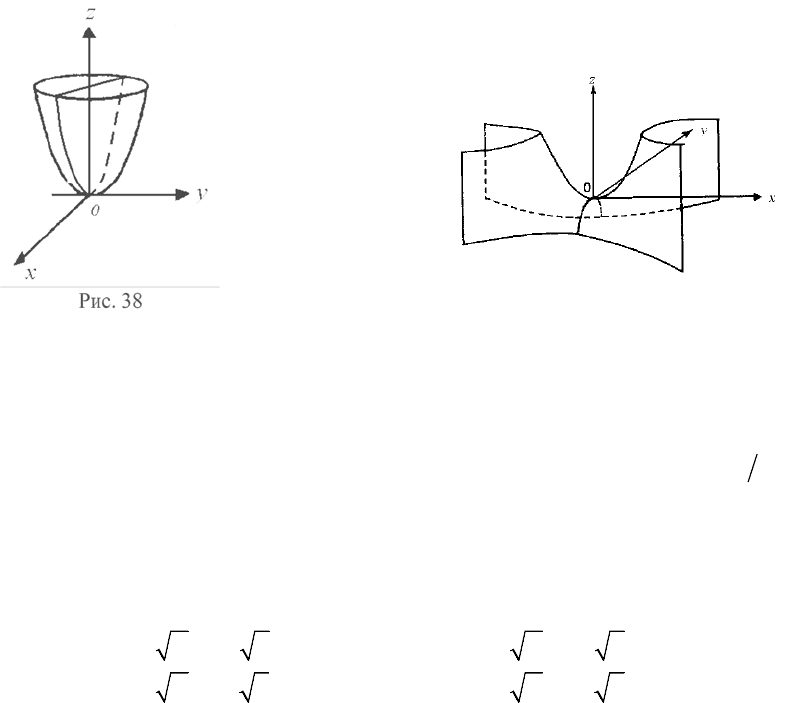
где и – заданные положительные числа. Расcекая поверхность (63) плос-
костью ( ), в сечении получим эллипс с полуосями и (см.
рис. 38). Поверхность (63) пересекается с плоскостью ( ) по параболе
а с плоскостью ( ) – по параболе При получим
параболоид вращения ( – ось вращения).
Гиперболический параболоид – это поверхность, определяемая уравнени-
ем
22
/ / 2,xpyq z−=
(64)
k
Oxyz
(,,)Mxyz
M
k
l
,,abc
zh=
||hc≥
||hc<
Oyz
0x =
Oxz
0y =
ab=
Oz
p
q
zh=
h ≥0
2hp
2hq
Oxz
0y =
2
2,x pz=
Oyz
0x =
2
2.y qz=
pq=
Oz
5354.ru
54
где и – заданные положительные числа. Поверхность (64) пересекается с
плоскостью ( ) по параболе ветви которой направлены в по-
ложительную сторону оси (рис. 39). Рассекая поверхность (64) плоско-
стью , получим кривую, определяемую системой уравнений
22
/ / 2,x pyq z
xh
−=
=
или
22
/ / 2,
,
hpyq z
xh
−=
=
(65)
Первое уравнение запишем так: Оно определяет на плос-
кости параболу с ветвями, направленными в отрицательную сторону оси
причём вершина параболы имеет координаты При
изменении h парабола (65) описывает поверхность, определяемую уравнени-
ем (64). Гиперболический параболоид содержит два семейства прямолиней-
ных образующих, определяемых системами уравнений
/ / 2,
/ / 1/ ,
x p y q kz
x pyq k
+=
−=
и
/ / 1/ ,
/ / 2,
x pyq l
x p y q lz
+=
−=
где и – произвольные постоянные. Доказательство проводится так же, как
и для однополостного гиперболоида.
p
q
Oxz
0y =
2
2,x pz=
Oz
xh=
22
2 ( /(2 )).y qz h p=−−
xh=
,Oz
2
, 0, (2 ).xhy zh p= = =
k
l
Рис. 39

55
ГЛАВА 3. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
§ 1. Определители высших порядков
Определитель четвёртого порядка содержит 16 элементов и обозначается
.
Как и раньше, элементы этого определителя обозначаются , где – номер
строки, – номер столбца, которым принадлежит элемент , ,
. Минором для элемента определителя ∆ называется опре-
делитель третьего порядка, получаемый вычёркиванием строки и столбца, ко-
торым принадлежит элемент . Зная этот минор, определим алгебраическое
дополнение для элемента определителя четвёртого порядка
. (1)
Определителем четвёртого порядка называется число
11 11 12 12 13 13 14 14
.aA aA aA aA∆= + + +
(2)
Таким образом, определитель четвёртого порядка выражается через опреде-
лители третьего порядка. Аналогично, с помощью определителя четвёртого
порядка введём понятие определителя пятого порядка, шестого порядка и т. д.
Зная определение определителя ( )-го порядка, введём понятие определи-
теля -го порядка
11 1
11 11 12 12 1 1
1
... .
n
nn
n nn
aa
aA aA aA
aa
∆= = + + +
(3)
Здесь – алгебраические дополнения элементов первой строки
. Эти алгебраические дополнения по формуле (1) выражаются
через миноры для соответствующих элементов первой строки. Миноры –
определители ( )-го порядка. Таким образом, определитель -го порядка
выражается по формуле (3) через определители ( )-го порядка. Соотноше-
ние (3) – разложение определителя -го порядка по элементам первой строки.
11 12 13 14
21 22 23 24
31 32 33 34
41 42 43 44
aaaa
aaaa
aaaa
aaaa
∆=
ij
a
i
j
ij
a
1,2,3,4i =
1,2,3,4j =
ij
M
ij
a
ij
a
ij
A
ij
a
( )
1
ij
ij ij
AM
+
= −
1n−
n
11 12 1
, ,,
n
AA A
11 12 1
, , ...,
n
aa a
ij
M
1n−
n
1n−
n

5354.ru
56
Элементы определителя образуют его главную диагональ.
Можно показать (принимается без доказательства), что определитель раскла-
дывается по элементам любой строки или любого столбца. Например, разло-
жения определителя по элементам -й строки и -го столбца имеют соответ-
ственно вид
11 2 2
... ,
i i i i in in
aA aA aA∆= + + +
(4)
11 22
... .
j j j j nj nj
aA aA aA∆= + + +
(5)
Таким образом, определитель равен сумме произведений элементов како-
го-либо ряда (строки или столбца) на их алгебраические дополнения.
§ 2. Свойства определителей
1. Определитель не изменится, если его столбцы сделать строками с теми
же номерами (эта операция называется транспонированием):
.
Доказательство этого свойства опускаем (оно основано на (4) и (5)).
2. Определитель лишь изменит знак, если поменять местами два каких-
либо ряда (две строки или два столбца). Например,
.
В справедливости последнего равенства убедимся, разложив определите-
ли слева и справа по элементам соответственно первого и второго столбцов.
3. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Чтобы доказать это свойство, достаточно переставить одинаковые ряды и
воспользоваться свойством 2.
4. Множитель, общий для элементов некоторого ряда определителя, мож-
но вынести за знак определителя. Например, пусть λ – определённое число,
тогда
.
11 22
, ,,
nn
aa a
i
j
11 1 11 21 1
1 12
nn
n nn n n nn
a a aa a
a a aa a
=
11 12 1 12 11 1
12 21
nn
n n nn n n nn
aa a aa a
aa a aa a
= −
11 1 11 1
11
nn
n nn n nn
a aaa
a a aa
λλ
= λ

57
Чтобы доказать это свойство, достаточно разложить определитель по эле-
ментам ряда, содержащим указанный множитель.
5. Если все элементы какой-либо строки (столбца) равны нулю, то опре-
делитель равен нулю. Это свойство доказывается разложением определителя
по нулевым элементам соответствующей строки (столбца).
6. Если к элементам некоторого ряда (строки или столбца) прибавить со-
ответствующие элементы другого ряда, умноженные на одно и то же число,
то определитель не изменится:
.
Чтобы доказать это свойство, нужно разложить определитель в правой ча-
сти по элементам первого столбца и учесть третье свойство.
7. Сумма произведений элементов какого-либо ряда определителя на ал-
гебраические дополнения соответствующих элементов другого параллельно-
го ряда равна нулю. Например,
11 21 12 22 1 2
0.
nn
aA aA aA+ ++ =
Рассматриваемое свойство доказывается разложением определителя по
элементам второго ряда с последующей заменой его элементов на соответ-
ствующие элементы первого ряда.
Приведенные выше свойства для определителей третьего порядка дока-
зываются проверкой.
§ 3. Матрицы и действия над ними. Обратная матрица
Матрицей называется прямоугольная таблица, содержащая
чисел,
имеющая строк и столбцов. Она обозначается
.
Числа называются элементами матрицы. Коротко эту матрицу
обозначают так: . Здесь – номер строки,
– номер столбца элемента . Матрицу иногда обозначают и так:
.
11 12 1
12
n
n n nn
aa a
aa a
=
11 12 12 1
1 22
n
n n n nn
a aa a
a aa a
+λ
+λ
mn
m
n
11 1
1
n
m mn
aa
A
aa
=
11 12
,,aa
( )
, 1, 2, , , 1, 2, ,
ij
Aaimjn= = =
i
j
ij
a
11 1
1
n
m mn
aa
aa

5354.ru
58
Если столбцы матрицы сделать строками с теми же номерами, то полу-
ченная матрица называется транспонированной и обозначается
11 1
1
.
m
n mn
aa
A
aa
′
=
Если в матрице число строк и число столбцов совпадают, то матрица
называется квадратной:
.
Элементы образуют главную диагональ матрицы. Число
называется порядком матрицы. Квадратной матрице можно поставить в со-
ответствие число, называемое определителем матрицы, обозначаемое и
равное
.
Матрица, у которой все элементы главной диагонали равны 1, а все
остальные элементы равны 0, называется единичной и обозначается
10
01
E
=
.
Матрица, состоящая из одной строки, называется строчной и обозначает-
ся . Матрица, состоящая из одного столбца, называется столб-
цевой, например,
.
Пусть даны две матрицы с одинаковым числом строк и столбцов:
Эти матрицы называются равны-
ми друг другу (при этом пишут или ), если все их соответству-
ющие элементы равны друг другу, т. е. для всех
11 1
1
n
n nn
aa
A
aa
=
11 22
, ,,
nn
aa a
n
( )
A∆
( )
11 1
1
n
n nn
aa
A
aa
∆=
( )
12
,,,
n
Y yy y=
1
2
n
x
x
X
x
=
( ) ( )
,,
ij ij
Aa Bb= =
1, 2, , , 1, 2, , .imjn= =
AB=
( ) ( )
ij ij
ab=
ij ij
ab=
1, 2, , , 1, 2, , .imjn= =
59
Суммой матриц и называется матрица, обозначаемая , эле-
менты которой для всех значений . Это правило можно записать
так: . Аналогично вводится понятие разности двух матриц.
Произведением матрицы на число λ называется матрица, обозначаемая
, элементы которой равны произведениям числа λ на соответствующие
элементы матрицы , т. е. . Иначе говоря, чтобы умножить мат-
рицу на число λ, нужно умножить на это число каждый её элемент (для срав-
нения заметим, что для умножения определителя на число нужно умножить
на это число все элементы какого-либо ряда).
Умножение матриц. Даны матрица , имеющая строк и
столбцов, и матрица , имеющая строк и столбцов. Произведением
этих матриц называется матрица, обозначаемая ( – первая матрица),
элементы которой определяются формулой
, , . (6)
Изобразим схематично эти матрицы и их произведение:
.
В формуле (6) первые индексы означают номера строки элемента матрицы,
вторые – номера столбца элемента. Формула (6) показывает, что элемент
-й строки и -го столбца матрицы равен сумме произведений элемен-
тов -й строки первой матрицы на соответствующие элементы -го столб-
ца второй матрицы . Следовательно, чтобы получить элементы
-й строки матрицы , нужно элементы -й строки умножить на соот-
ветствующие элементы первого столбца , и, сложив, найти . Умножив
элементы -й строки на соответствующие элементы второго столбца и
сложив, получим и т. д. Умножив элементы -й строки на соответству-
ющие элементы -го столбца и сложив, получим .
Таким образом, элементы -й строки матрицы С получаются с помощью
-й строки первой матрицы . Это относится к любой строке матрицы С. По-
этому ясно, что число строк С равно числу строк , а число столбцов рав-
но числу столбцов матрицы В, так как номер столбца элемента совпадает
с номером столбца матрицы .
A
B
C AB= +
ij ij ij
cab= +
,ij
( ) ( ) ( )
ij ij ij ij
a b ab+=+
A
Aλ
A
( ) ( )
ij ij
aaλ=λ
( )
ij
Aa=
m
k
( )
ij
Bb=
k
n
C AB=
A
ij
c
11 2 2ij i j i j ik kj
c ab ab ab= + ++
1, 2, ,im=
1, 2, ,jn=
11 1 11 1 1 11 1 1
11
11 1
k jn j n
i ik i ij in
m mk k kj kn m mj mn
a ab b b c c c
a a ccc
a ab b b c c c
=
ij
c
i
j
C AB=
i
A
j
B
12
,,,
i i in
cc c
i
C AB=
i
A
B
1i
c
i
A
B
2i
c
i
A
n
B
in
c
i
i
A
A
C
j
ij
c
j
B

5354.ru
60
Аналогично найдём , если число столбцов матрицы равно числу
строк матрицы . Если это не так, то произведения не существует. Если
даже и существуют, то легко проверить на примерах, что, вообще го-
воря, .
Свойства умножения матриц. Пусть даны три матрицы , и . Тогда
; .
Пусть – квадратная матрица, а – единичная матрица того же порядка,
что и . Нетрудно проверить, что .
Обратная матрица. Пусть дана квадратная матрица
Определитель этой матрицы есть число
.
Пусть этот определитель не равен нулю и – алгебраическое дополнение
для элемента .
Обратной к данной матрице называется матрица, обозначаемая и
равная
.
Нетрудно проверить, что
11
.AA A A E
−−
= =
Отсюда видно, что для построения обратной матрицы для матрицы
нужно:
• элементы заменить на их алгебраические дополнения;
• все дополнения поделить на – определитель матрицы ;
• полученную матрицу транспонировать.
Из приведенного определения видно, что для нахождения нужно вы-
числить определитель матрицы и все алгебраические дополнения для
всех ее элементов.
1
C BA=
B
A
BA
AB
BA
AB BA≠
A
B
C
( ) ( )
A BC AB C=
( )
A B C AB AC+= +
A
E
A
AE EA A= =
11 1
1
n
n nn
aa
A
aa
=
( )
11 1
1
n
n nn
aa
A
aa
∆=
ij
A
ij
a
A
1
A
−
( ) ( )
( ) ( )
1
11
1
1
n
n nn
A
A
AA
A
AA
AA
−
∆∆
=
∆∆
1
A
−
A
A
( )
A∆
A
1
A
−
( )
A∆
