Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

684 Chapter 13 Computational Geometry Topics
else
return -1;
} else {
// type is COINCIDENT
for (each edge T.coincident[i]) {
if (P on T.coincident[i])
return 0;
}
// does not matter which subtree you use
if (T.posChild exists)
return PointLocation(T.posChild, P);
else if (T.negChild exists)
return PointLocation(T.negChild, P);
else {
// Theoretically you should not get to this block. Numerical
// errors might cause the block to be reached, most likely
// because the test point is nearly an end point of a
// coincident edge. An implementation could throw an exception
// or ‘assert’ in Debug mode, but still return a value in Release
// mode. For simplicity, let’s just return 0 in hopes the test
// point is nearly a coincident edge end point.
return 0;
}
}
}
13.1.4 Partitioning a Line Segment by a BSP Tree
Given a line segment in the plane, the segment is naturally partitioned by a BSP tree
into subsegments that are contained by an outside region, contained by an inside
region, or coincident to splitting lines. The line segment is processed at each node
of the tree. If the segment is on the positive side of the line, possibly with one end
point on the line, it is just sent to the positive-child subtree for further processing. If
the node has no positive-child subtree, then the line segment is in an outside region.
Similarly, if the segment is on the negative side of the line, it is further processed
by the negative-child subtree unless that subtree does not exist, in which case the line
segment is in an inside region. If the segment crosses the splitting line, it is partitioned
into two pieces, one piece on the positive side of the line and one piece on the negative
side. The positive piece is further processed by the positive-child subtree; the negative
piece is further processed by the negative-child subtree. The final possibility is that the
segment is coincident with the splitting line. The intersection of the segment with an
edge generating the splitting line must be calculated. Any subsegments not contained
13.1 Binary Space-Partitioning Trees in 2D 685
by an edge must be further processed by both the positive-child and negative-child
subtrees.
The end result of processing the line segment is a partition, a representation of
the line segment as a union of contiguous subsegments. Each subsegment lives in an
inside region, an outside region, or is on a polygon boundary. Those segments on
the polygon boundary can be further classified based on the direction of the polygon
edge and the direction of the line segment. This distinction is important when using
BSP trees to support Boolean operations on polygons. Figure 13.2 shows a splitting
line and two segments, E
0
and E
1
, that are coincident to the line. E
0
and N are in the
same direction, but E
1
and N are in opposite directions.
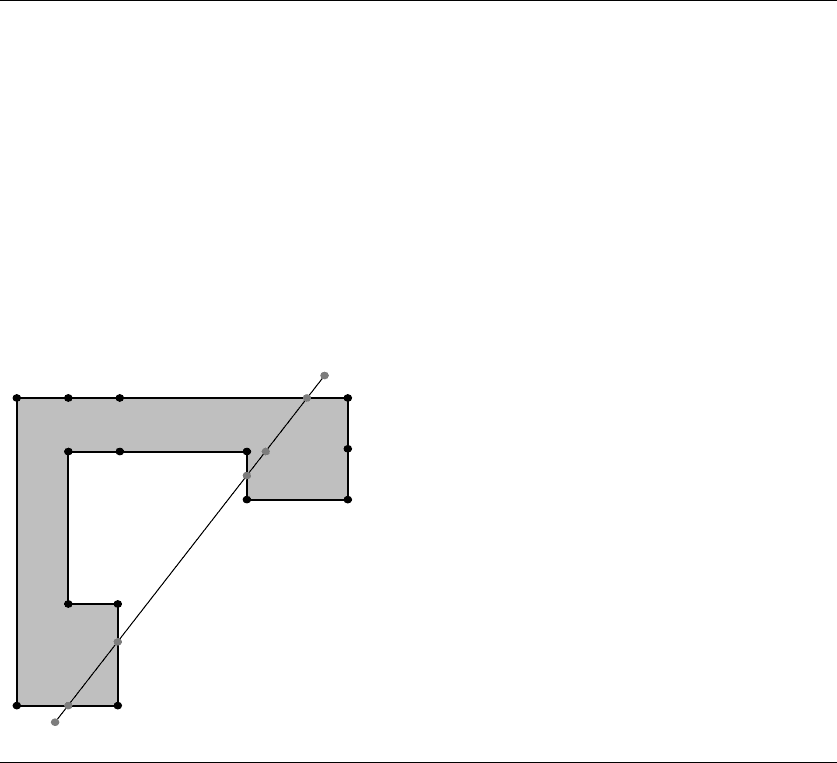
Figure 13.12 shows the polygon of Figure 13.3 and a line segment intersecting
the polygon. The end points of the line segment are labeled as 0 and 1. The other
labeled points, 2 through 6, are inserted into the partition as the segment is processed
recursively through the tree. The right portion of the figure shows the BSP tree for the
polygon. The segments are denoted by (i
0
, i
1
). Initially segment (0, 1) is processed at
the root node of the tree. The segment is not split by the line containing edge 9, 0,
so region 0 does not contain any portion of the original segment. The segment (0, 1)
is sent to the negative child of the root and processed. The segment is split by the
line containing edge 0, 1, the new point labeled 2. Segment (0, 2) is on the positive
side of the splitting line, but the root node has no positive child, so segment (0, 2) is
contained in region 1. Segment (2, 1) is sent to the negative child and the process is
repeated.
The final partition leads to positive segments (0, 2), (3, 5), and (6, 1). The negative
segments are (2, 3), (5, 4), and (4, 6). Observe that the subsegments do not necessarily
alternate between positive and negative. In the previous example, the subsegments
(5, 4) and (4, 6) are adjacent, but both negative. An implementation of line segment
partitioning can trap these cases and combine adjacent same-sign segments into
single segments.
The pseudocode for line segment partitioning is listed below. The inputs are the
tree, polygon, and line segment end points V
0
and V
1
. The outputs are the four sets of
subsegments. The
Pos set contains those subsegments that are in positive regions, and
the
Neg set contains those subsegments that are in negative regions. The other two sets
store subsegments that are contained by edges that are coincident to splitting lines.
The
CoSame set contains subsegments contained by edges where each subsegment is
in the same direction as the edge. The
CoDiff set contains subsegments contained by
edges where each subsegment is in the opposite direction as the edge.
void GetPartition(BspTree T, Edge E, EdgeSet Pos, EdgeSet Neg,
EdgeSet CoSame, EdgeSet CoDiff)
{
type = Classify(T.line, E, SubPos, SubNeg);
if (type is CROSSES) {
GetPosPartition(T.posChild, SubPos, Pos, Neg, CoSame, CoDiff);
GetNegPartition(T.negChild, SubNeg, Pos, Neg, CoSame, CoDiff);
} else if (type is POSITIVE) {
686 Chapter 13 Computational Geometry Topics
GetPosPartition(T.posChild, E, Pos, Neg, CoSame, CoDiff);
} else if (type is NEGATIVE) {
GetNegPartition(T.negChild, E, Pos, Neg, CoSame, CoDiff);
} else {
// type is COINCIDENT
// construct segments of E intersecting coincident edges
A = {E};
for (each edge E’ in T.coincident)
A = Intersection(A, E’);
for (each segment S of A) {
if (S is in the same direction as T.line)
CoPos.Insert(S);
else
CoNeg.Insert(S);
}
// construct segments of E not intersecting coincident edges
B={E}-A;
for (each segment S of B) {
GetPosPartition(T.posChild, S, Pos, Neg, CoSame, CoDiff);
GetNegPartition(T.negChild, S, Pos, Neg, CoSame, CoDiff);
}
}
}
void GetPosPartition(BspTree T, Edge E, EdgeSet Pos, EdgeSet Neg,
EdgeSet CoSame, EdgeSet CoDiff)
{
if (T.posChild)
GetPartition(T.posChild, E, Pos, Neg, CoSame, CoDiff);
else
Pos.Insert(E);
}
void GetNegPartition(BspTree T, Edge E, EdgeSet Pos, EdgeSet Neg,
EdgeSet CoSame, EdgeSet CoDiff)
{
if (T.negChild)
GetPartition(T.negChild, E, Pos, Neg, CoSame, CoDiff);
else
Neg.Insert(E);
}
The function Classify is the same one used for BSP tree construction.
13.2 Binary Space-Partitioning Trees in 3D 687
2
2
3
3
410 5
5
4
67
12
10
0
9
13 11
1
8
6
r <0,9> process (0,1)
p [region 0] final = nothing
n <0,1> process(0,1), add 2
p [region 1] final = (0,2)
n <1,2> process (2,1), add 3
p <10,5> process (3,1), add 4
p <5,6> process (3,4), add 5
p [region 2] final = (3,5)
n <6,7> process (5,4)
p [region 3] final = nothing
n <7,12> process (5,4)
p [region 4] final = nothing
n [region 5] final = (5,4)
n <12,8> process (4,1)
p [region 6] final = nothing
n <8,11> process (4,1), add 6
p [region 7] final = (6,1)
n [region 8] final = (4,6)
n <2,3> process (2,3)
p <3,4>
p <4,10>
p [region 10]
n <11,13>
p [region 11]
n [region 12]
n <13,9>
p [region 13]
n [region 14]
n [region 9] final = (2,3)
Figure 13.12 Partition of a line segment.
13.2 Binary Space-Partitioning Trees in 3D
We recommend reading Section 13.1 before reading this section to obtain intuition
about binary space partitioning.
Consider a plane in space with representation n · X −c =0. The plane partitions
space into two half-spaces. The half-space on the side of the plane to which n points is
called the positive side of the plane; the other side is called the negative side of the plane.
If X is on the positive side, then n · X −c>0, hence the use of the phrase “positive
688 Chapter 13 Computational Geometry Topics
side.” If X is on the negative side, then n ·X −c<0.ApointX on the plane of course
satisfies n · X −c =0.
Each half-space may be further subdivided by another plane in space. The re-
sulting positive and negative regions can themselves be subdivided. The resulting
partitioning of the plane is represented by a binary tree, each node representing the
splitting plane. The left child of a node corresponds to the positive side of the splitting
plane that the node represents; the right child corresponds to the negative side. The
leaf nodes of the tree represent the convex regions obtained by the partitioning.
13.2.1 BSP Tree Representation of a Polyhedron
Just as a 2D BSP tree is used to partition a polygon into convex subpolygons, a 3D
BSP tree can be used to partition a polyhedron into convex subpolyhedra. The de-
composition is useful for point-in-polyhedron queries and Boolean operations on
polyhedra. The simplest construction uses polygon faces to determine the splitting
planes. The recursive splitting is applied, just as in 2D, the only complication being
that computing the intersection of a convex polygon and a plane is slightly more dif-
ficult than computing the intersection of a line segment and a line. The pseudocode
for construction of a BSP tree from a polyhedron is listed below. As a reminder, we
require that the polyhedron faces are convex polygons.
BspTree ConstructTree(FaceList L)
{
T = new BspTree;
// use a face to determine the splitting plane for the tree node
T.plane = GetPlaneFromFace(L.first); // Dot(N, X)-c=0
FaceList posList, negList; // initially empty lists
for (each face F of L) {
// Determine how face and plane relate to each other. If the face
// crosses the plane, the subpolyhedra on the positive and
// negative side of the plane are returned.
type = Classify(T.plane, F, SubPos, SubNeg);
if (type is CROSSES) {
// Dot(N, X)-c<0forsome vertices,
// Dot(N, X)-c>0forsome vertices
posList.AddFace(SubPos);
negList.AddFace(SubNeg);
} else if (type is POSITIVE) {
// Dot(N, X)-c>=0forallvertices, at least one positive
posList.AddFace(F);
13.2 Binary Space-Partitioning Trees in 3D 689
} else if (type is NEGATIVE) {
// Dot(N, X)-c<=0forallvertices, at least one negative
negList.AddFace(F);
} else {
// type is COINCIDENT
// Dot(N, X)-c=0forallvertices
T.coincident.AddFace(F);
}
}
if (posList is not empty)
T.posChild = ConstructTree(posList);
else
T.posChild = null;
if (negList is not empty)
T.negChild = ConstructTree(negList);
else
T.negChild = null;
return T;
}
The function GetPlaneFromFace produces a plane whose normal vector points to
the outside region of the polyhedron at the specified face. Other coincident faces may
or may not have normals that point in the same direction as the plane normal. This
is analogous to the situation shown in Figure 13.2 for the 2D polygon case.
The function
Classify tries to find a line segment of intersection of the current
face and the node’s plane. If there is an intersection that is an interior segment of the
face, the positive and negative subfaces are returned. If the face is only on the positive
side, with the possibility that some vertices or collinear edges are on the plane, then
the face is classified as a positive face. A similar classification is given for faces on the
negative side of the plane. The face can be entirely on the splitting plane, in which
case the face is classified as coincident. The pseudocode for this function is
int Classify(Plane P, Face F, Face SubPos, Face SubNeg)
{
for (i = 0; i < F.vertexQuantity; i++)
d[i] = Dot(P.normal, F.V(i) - P.origin);
if (at least one d[i] > 0 and at least one d[i] < 0) {
// face crosses plane
SplitPolygon(F, P, d[], SubPos, SubNeg);
return CROSSES;
690 Chapter 13 Computational Geometry Topics
} else if (all d[i] >= 0 with at least one d[i] > 0) {
// All vertices of the face are on the positive side of the plane,
// but not all vertices are on the plane.
return POSITIVE;
} else if (all d[i] <= 0 with at least one d[i] < 0) {
// All vertices of the face are on the negative side of the plane,
// but not all vertices are on the plane.
return NEGATIVE;
} else {
// All vertices of the face are on the plane.
return COINCIDENT;
}
}
The function SplitPolygon determines those edges of F that intersect the plane
(computable by the
d[] values) and constructs the two subpolygons. The points of in-
tersection of the edges with the plane are computed just like the point of intersection
between edge and line was computed for the 2D problem. Floating-point round-off
errors must be dealt with by an implementation when one or more of the
d[i] are
nearly zero. This is particularly important to avoid unnecessary splits.
13.2.2 Minimum Splits versus Balanced Trees
In the 2D problem, a convex polygon led to a BSP tree that was a linear list. A convex
polyhedron also has a BSP tree that is a linear list since the faces of the polyhedron
are always on the negative side of a plane of one of the faces. A balanced tree was
constructed in the 2D case by selecting a splitting line connecting two nonadjacent
vertices. The convexity of the polygon guaranteed that the splitting line did not split
any edges of the polygon. The resulting tree was the best of both worlds: it was
balanced and required no edge splitting.
The situation in 3D is not as simple. A splitting plane may be chosen that cuts the
convex polyhedron in two pieces, but the plane in most cases will require splitting
faces. The only situation where the splitting will not occur is if the plane intersects
the polyhedron only at edges. That means the polyhedron must contain a polyline
of edges that is coplanar—a situation that is not generic. Consequently, obtaining a
balanced tree will require some splitting, the hope being that the number of splits is as
small as possible. Selecting a heuristic that leads to a generic algorithm for minimum
splitting is difficult at best. Greater success is more likely if an implementation uses a
priori knowledge about its data sets. In any event, the quality of the algorithm used
to build the tree is the key to the performance of a BSP tree system.
13.2 Binary Space-Partitioning Trees in 3D 691
13.2.3 Point in Polyhedron Using BSP Trees
Computing the location of a point relative to a polyhedron is exactly the same algo-
rithm as in the 2D problem. The point is compared against each node of the BSP tree.
If the point is on the positive side of a plane, and if the positive child exists, the point
is further processed by that subtree. If the positive child does not exist, the point is
outside the polyhedron. If the point is on the negative side of a plane, and if the neg-
ative child exists, the point is further processed by that subtree. If the negative child
does not exist, the point is inside the polyhedron. If the point is on the splitting plane
itself, it is either contained by a face, in which case the point is on the polyhedron
itself, or the point is not contained by a face and it is sent to any existing child subtree
for further processing. The pseudocode is shown below. The return value is +1 if the
point is outside, −1 if the point is inside, or 0 if the point is on the polyhedron.
int PointLocation(BspTree T, Point P)
{
// test point against splitting plane
type = Classify(T.plane, P);
if (type is POSITIVE) {
if (T.posChild exists)
return PointLocation(T.posChild, P);
else
return +1;
} else if (type is NEGATIVE) {
if (T.negChild exists)
return PointLocation(T.negChild, P);
else
return -1;
} else {
// type is COINCIDENT
for (each face T.coincident[i]) {
if (P on T.coincident[i])
return 0;
}
// does not matter which subtree you use
if (T.posChild exists)
return PointLocation(T.posChild, P);
else if (T.negChild exists)
return PointLocation(T.negChild, P);
else
return 0;
}
}
692 Chapter 13 Computational Geometry Topics
13.2.4 Partitioning a Line Segment by a BSP Tree
Given a line segment in space, the segment is naturally partitioned by a BSP tree into
subsegments that are contained by an outside region, contained by an inside region,
or coincident to splitting planes. The line segment is processed at each node of the
tree. If the segment is on the positive side of the plane, possibly with one end point
on the plane, it is just sent to the positive-child subtree for further processing. If the
node has no positive-child subtree, then the line segment is in an outside region.
Similarly, if the segment is on the negative side of the plane, it is further processed
by the negative-child subtree unless that subtree does not exist, in which case the
line segment is in an inside region. If the segment crosses the splitting plane, it is
partitioned into two pieces, one piece on the positive side of the line and one piece
on the negative side. The positive piece is further processed by the positive-child
subtree; the negative piece is further processed by the negative-child subtree. The final
possibility is that the segment is coincident with the splitting plane. The intersection
of the line segment with the faces contained by the splitting plane must be calculated.
Observe that this is exactly the problem of finding the intersection of a line segment
with a 2D polygon, a problem that can be solved using 2D BSP trees. However, since
the faces are required to be convex polygons, the intersection of line segment and
convex polygon can be implemented in a straightforward manner without having
to create BSP trees for the faces. Any subsegments not contained by a face must be
further processed by both the positive-child and negative-child subtrees.
The end result of processing the line segment is a partition—a representation of
the line segment as a union of contiguous subsegments. Each subsegment lives in an
inside region, an outside region, or is on a polygon boundary. The pseudocode for
the partitioning is listed below.
void GetPartition(BspTree T, Edge E, EdgeSet Pos, EdgeSet Neg, EdgeSet Coin)
{
type = Classify(T.plane, E, SubPos, SubNeg);
if (type is CROSSES) {
GetPosPartition(T.posChild, SubPos, Pos, Neg, Coin);
GetNegPartition(T.negChild, SubNeg, Pos, Neg, Coin);
} else if (type is POSITIVE) {
GetPosPartition(T.posChild, E, Pos, Neg, Coin);
} else if (type is NEGATIVE) {
GetNegPartition(T.negChild, E, Pos, Neg, Coin);
} else {
// type is COINCIDENT
// construct segments of E intersecting coincident faces
A = {E};
for (each face F in T.coincident)
A = Intersection(A, F);
13.2 Binary Space-Partitioning Trees in 3D 693
for (each segment S of A)
Coin.Insert(S);
// construct segments of E not intersecting coincident faces
B={E}-A;
for (each segment S of B) {
GetPosPartition(T.posChild, S, Pos, Neg, Coin);
GetNegPartition(T.negChild, S, Pos, Neg, Coin);
}
}
}
void GetPosPartition(BspTree T, Edge E, EdgeSet Pos, EdgeSet Neg, EdgeSet Coin)
{
if (T.posChild)
GetPartition(T.posChild, E, Pos, Neg, Coin);
else
Pos.Insert(E);
}
void GetNegPartition(BspTree T, Edge E, EdgeSet Pos, EdgeSet Neg, EdgeSet Coin)
{
if (T.negChild)
GetPartition(T.negChild, E, Pos, Neg, Coin);
else
Neg.Insert(E);
}
The function Classify in BSP tree construction splits a face, but the Classify
function used in this routine has the simpler job of splitting only an edge.
The line segment does not necessarily have to represent a geometric entity con-
sisting of a continuum of points at a given time. For example, in a collision detection
system where a point abstractly represents an object moving through space that is
partitioned by a BSP tree, the line segment can represent the predicted path of mo-
tion of the point over a specified time interval. If the object represented by the point
is not allowed to pass through a “wall” (contained in a partitioning plane of the BSP
tree) separating an inside region from an outside one, the line segment partitioning
can be used to prevent the object from doing so. If the segment has to be split by par-
titioning planes, the shortest subsegment containing the initial point (at time zero)
represents how far the object can move without a collision. The application can then
move the object by that distance or, if desired, disallow any motion. Such an approach
for collision detection is superior to one that samples the projected path to generate
a lot of points, then processes each one by the BSP tree to see if it is contained by an
