Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

694 Chapter 13 Computational Geometry Topics

inside or an outside region, then collectively analyzes the results to decide how far an

object can move.

13.2.5 Partitioning a Convex Polygon by a BSP Tree

Partitioning a convex polygon by a 3D BSP tree is the direct analog of partitioning

a line segment by a 2D BSP tree. The pseudocode is listed below. The input face

F is assumed to be a convex polygon. The most complex part of the algorithm is

handling the cases when the polygon is coincident to a splitting plane, in which case

the problem is reduced to computing an intersection and a difference of polygons

in a plane. Section 13.5 shows how to compute the intersection and difference of

polygons.

void GetPartition(BspTree T, Face F, FaceSet Pos, FaceSet Neg,

FaceSet CoPos, FaceSet CoNeg)

{

type = Classify(T.plane, F, SubPos, SubNeg);

if (type is CROSSES) {

GetPosPartition(T.posChild, SubPos, Pos, Neg, CoPos, CoNeg);

GetNegPartition(T.negChild, SubNeg, Pos, Neg, CoPos, CoNeg);

} else if (type is POSITIVE) {

GetPosPartition(T.posChild, F, Pos, Neg, Coin);

} else if (type is NEGATIVE) {

GetNegPartition(T.negChild, F, Pos, Neg, Coin);

} else {

// type is COINCIDENT

// compute intersection of F with coincident faces

A = {F};

for (each face F’ in T.coincident)

A = Intersection(A, F’);

for (each face S of A) {

if (S has normal in same direction as T.plane)

CoPos.Insert(S);

else

CoNeg.Insert(S);

}

// construct complement of intersection of F with coincident faces

B={F}-A;

for (each face S of B) {

GetPosPartition(T.posChild, S, Pos, Neg, CoPos, CoNeg);

GetNegPartition(T.negChild, S, Pos, Neg, CoPos, CoNeg);

13.3 Point in Polygon 695

}

void GetPosPartition(BspTree T, Face F, FaceSet Pos, FaceSet Neg,

FaceSet CoPos, FaceSet CoNeg)

{

if (T.posChild)

GetPartition(T.posChild, F, Pos, Neg, CoPos, CoNeg);

else

Pos.Insert(F);

}

void GetNegPartition(BspTree T, Face F, FaceSet Pos, FaceSet Neg,

FaceSet CoPos, FaceSet CoNeg)

{

if (T.negChild)

GetPartition(T.negChild, F, Pos, Neg, CoPos, CoNeg);

else

Neg.Insert(F);

}

13.3 Point in Polygon

A common query in graphics applications is to determine if a point is inside a poly-

gon. Many approaches can be used to answer the query. A survey of these approaches

is in the section “Point in Polygon Strategies” in Heckbert (1994). If the polygon is

represented as a BSP tree, Section 13.1 discusses how to determine if a point is inside

or outside the polygon. We discuss here a few methods that do not require prepro-

cessing to create data structures that support fast queries. The last section discusses a

method that does require preprocessing by decomposing the polygon into trapezoids.

13.3.1 Point in Triangle

Consider a point P and a triangle with noncollinear vertices V

for 0 ≤ i ≤ 2. Let

the triangle edges be e

= V

− V

, e

= V

− V

, and e

= V

− V

. Edge normals

are n

=Perp(e

),wherePerp(x, y) = (y, −x). The normals are outer-pointing if the

vertices are counterclockwise ordered or inner-pointing if the vertices are clockwise

ordered.

In the case of counterclockwise-ordered vertices, P is inside the triangle if it is on

the negative side of each edge line n

· (X −V

) = 0. That is, P is inside the triangle

when n

·(P − V

)<0 for all i. The point is outside the triangle if n

·(P − V

)>0

696 Chapter 13 Computational Geometry Topics

for at least one i. It is possible that P is on the triangle boundary itself, in which case

n

·(P −V

) ≤0 for all i with equality for at least one i. If an equality occurs once, the

point is on an edge but not at a vertex. If an equality occurs twice, the point is a vertex.

It is not possible for equality to occur three times. If the vertices are clockwise ordered,

the inequalities on these tests are simply reversed. In an application where the vertex

ordering is not consistent among all triangles, the test for point inside triangle that

works regardless of order is

(n

· (V

− V

))(n

· (P −V

)) > 0 for all i

Of course, the ﬁrst dot product effectively determines the vertex ordering.

The point can also be written in barycentric coordinates as P = c

+ c

,wherec

+ c

= 1. P is inside or on the triangle if 0 ≤ c

≤ 1 for all i.

If c

< 0 for at least one j , the point is outside the triangle. The coefﬁcient c

computed in the following manner:

P − V

= (c

− 1)V

+ c

= (−c

− c

+ c

= c

− V

) + c

− V

)

so that n

· (P − V

) = c

n

· (V

− V

). Similar constructions apply for c

and c

obtain

=−

n

· (P −V

)

n

·e

, c

=−

n

· (P −V

)

n

·e

, c

=−

n

· (P −V

)

n

·e

The exact representation of P is not important for testing if it is inside the triangle.

The denominators of the fractions are all the same sign for a given triangle ordering,

so the signs of the numerators are all that matter for the query. These signs are exactly

what is considered in the test provided earlier in this section.

Although we assumed that the triangle vertices are noncollinear, applications

might need to deal with the degenerate case of collinear vertices. More likely is that a

triangle that is needlelike or has small area might be encountered in a data set. Such a

triangle satisﬁes the noncollinear condition, but ﬂoating-point round-off errors can

create problems.

Consider the case of three distinct vertices that are collinear, so the triangle is

degenerate and is a line segment. One of the vertices must be an interior point to

the edge connecting the other two vertices. For the sake of argument, suppose V

that vertex. The normal vectors are mutually parallel, but n

points in the opposite

direction of n

and n

.IfP is not on the line of the vertices, then Sign(n

· (P −

)) =−Sign(n

· (P − V

)) and Sign(n

· (P − V

)) = Sign(n

· (P − V

)).Itis

not possible for all three signs to be the same, so the point-in-triangle sign tests

mentioned previously still produce the correct result, that P is outside the triangle

(in this case, not on the line segment). If P is on the line of the vertices, then all three

signs are zero—not enough information to determine if P is contained by the line

segment. Further work must be done to resolve the problem. Speciﬁcally, P must be

13.3 Point in Polygon 697

a linear combination of the segment end points, P =(1 − t)V

+tV

for some value

t.Ift ∈ [0, 1], then P is contained by the line segment and P is “inside” the triangle.

Otherwise it is outside. This type of analysis also occurs in the construction of the

convex hull of a point set in 2D (Section 13.7).

If the triangle is needlelike, nearly collinear vertices, so to speak, ﬂoating-point

round-off errors can make the situation look just like the collinear one. The same

problem can occur if two of the vertices are nearly the same. In either case, an appli-

cation has two options. The ﬁrst is to preprocess the triangles to collapse nearly de-

generate ones to line segments or points, then use point equality, point-in-segment,

or point-in-triangle tests accordingly. This approach is recommended if a large num-

ber of containment queries will occur for the same collection of triangles. The second

is to accept the triangles as is and test for the degeneracies and switch to the point

equality or point-in-segment test as needed.

13.3.2 Point in Convex Polygon

The sidedness tests used in the point-in-triangle query naturally extend to determin-

ing if a point is in a convex polygon. Let the convex polygon have counterclockwise-

ordered, noncollinear vertices {V

}

n−1

i=0

with the convention that V

= V

.Ifthever-

tices are collinear or the polygon is nearly degenerate in that it is needlelike, the

potential numerical problems are handled in the same way as described in the point-

in-triangle tests.

The edges of the polygon are e

= V

i+1

− V

, and outer-pointing edge normals

are n

= Perp(e

). The point P is inside the polygon when n

· (P − V

)<0 for all

i. The point is outside if n

· (P − V

)>0 for some i. The point is on the polygon

boundary itself if n

· (P − V

) ≤ 0 for all i with equality occurring for at least one i.

If equality occurs for exactly one i, then P is on an edge but is not a vertex. If equality

occurs for two values of i, the point is a vertex. Equality cannot occur for three or

more indices.

This algorithm is O(n) since all n edges of the polygon must be tested to know

that P is inside. The straightforward implementation for testing if a point is inside or

on the polygon is

bool PointInPolygon(Point P, ConvexPolygon C)

{

for (i0 = 0, i1 = C.N - 1; i < C.N; i0++) {

if (Dot(Perp(C.V(i0) - C.V(i1)), P - C.V(i1)) > 0)

return false;

}

return true;

}

When P is inside the polygon, the loop body is executed n times.

698 Chapter 13 Computational Geometry Topics

An Asymptotically Faster Method

Another algorithm uses the bisection method that was also used to build a balanced

BSP tree for a convex polygon. To illustrate, consider a convex quadrilateral with

counterclockwise-ordered vertices V

for 0 ≤i ≤3. The polygon is treated as a union

of two triangles, V

, V

 and V

, V

. The bisection implementation is

bool PointInConvexQuadrilateral(Point P, ConvexPolygon C)

{

if (Dot(Perp(C.V(2) - C.V(0)), P - C.V(0)) > 0) {

// P potentially in <V0, V1, V2>

if (Dot(Perp(C.V(1) - C.V(0)), P - C.V(1)) > 0) return false;

if (Dot(Perp(C.V(2) - C.V(1)), P - C.V(1)) > 0) return false;

} else {

// P potentially in <V0, V2, V3>

if (Dot(Perp(C.V(3) - C.V(2)), P - C.V(3)) > 0) return false;

if (Dot(Perp(C.V(0) - C.V(3)), P - C.V(3)) > 0) return false;

}

return true;

}

When P is inside the quadrilateral, three dot products are computed. The

straightforward implementation computes four dot products. However, the straight-

forward implementation identiﬁes some outside points with a single dot product

(points outside the ﬁrst edge), but the bisection for a quadrilateral requires a mini-

mumoftwodotproductsbeforerejection.Forageneralconvexpolygon,thebisec-

tion implementation is

int GetMiddleIndex(int i0, int i1, int N)

{

if (i0 < i1)

return (i0 + i1) / 2;

else

return (i0 + i1 + N) / 2 (mod N);

}

bool PointInSubpolygon(Point P, ConvexPolygon C, int i0, int i1)

{

if (i1 - i0 is 1 modulo C.N)

return Dot(Perp(C.V(i1) - C.V(i0)), P - C.V(i0)) <= 0;

mid = GetMiddleIndex(i0, i1);

if (Dot(Perp(C.V(mid) - C.V(i0)), P - C.V(i0)) > 0) {

// P potentially in <V(i0), V(i0 + 1), ... ,V(mid - 1), V(mid)>

13.3 Point in Polygon 699

return PointInSubpolygon(P, C, i0, mid);

} else {

// P potentially in <V(mid), V(mid + 1), ... ,V(i1 - 1), V(i1)>

return PointInSubpolygon(P, C, mid, i1);

}

bool PointInPolygon(Point P, ConvexPolygon C)

{

return PointInSubpolygon(P, C, 0, 0);

}

The vertex indices are computed modulo C.N. Because of the bisection, the algo-

rithm is O(log n) for a convex polygon with n vertices.

Another Asymptotically Faster Method

The method described in this subsection also requires O(log n) time to perform the

point-in-convex-polygon query.

The polygon vertices V

for 0 ≤ i<nare assumed to be stored in counterclock-

wise order. Extreme vertices in the x-direction are computed. This can be done in

O(log n) time using the bisection method discussed in Section 7.7.2.The x-minimum

vertex has index i

min

, and the x-maximum vertex has index i

max

. Observe that it is not

necessary that i

min

max

. As the vertices are counterclockwise traversed from V

min

to V

max

, the corresponding edges have outer normal vectors whose y-components are

negative or zero, the latter occurring at most twice if the polygon has vertical edges at

either x-extreme. The corresponding vertices and edges are referred to as the bottom

half of the polygon. Similarly, as the vertices are counterclockwise traversed from V

max

to V

min

, the corresponding edges have outer normal vectors whose y-components are

positive or zero. The corresponding vertices and edges are referred to as the top half

of the polygon.

Let P be the point to be tested for containment. The index bisection method is

used to determine which vertex V

in the top half of the polygon has the smallest

x-value larger or equal to the x-value of P . If the top half has vertical edges, the

extreme indices found initially can be appropriately incremented or decremented to

exclude those edges from this test without affecting the correctness of the algorithm.

Similarly, index bisection can be used to determine which vertex V

in the bottom

half of the polygon has the largest x-value smaller or equal to the x-value of P . Both

bisections are O(log n) in time.

The vertical line containing P intersects the two directed edges whose initial

points are V

and V

.IfP is between the two edges, then it is inside the polygon.

Otherwise it is outside the polygon. Figure 13.13 illustrates the various concepts in

this section.

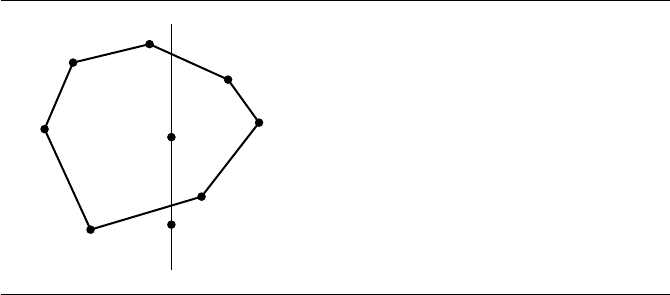
700 Chapter 13 Computational Geometry Topics

min

max

Figure 13.13 Point-in-convex-polygon test by determining two edges intersected by the vertical

line through the test point. P is inside the polygon. Q is outside the polygon.

13.3.3 Point in General Polygon

Perhaps the most used and effective algorithm for determining if P is inside a general

polygon involves analyzing the intersections of the polygon and a ray whose origin

is P and whose direction is (1, 0). The idea is effectively the same one used in line

segment partitioning by a BSP tree. As a ray is traversed starting from P , each time

an edge is transversely crossed, a switch is made from inside to outside or vice versa.

An implementation keeps track of the parity of the crossings. Odd parity means P is

inside, even parity means it is outside. Figure 13.14 illustrates this.

To illustrate some technical difﬁculties, the ﬁgure includes polygon edges that are

coincident to the ray for P

and polygon vertices that are on the ray. The problem

at the polygon vertex 10 is that the ray transversely intersects the polygon boundary

at that vertex, so the intersection should count as only one crossing. However, the

two edges sharing the vertex are processed separately, each edge indicating that the

crossing at the vertex is transverse. The result is that the vertex is counted twice as a

crossing, incorrectly reversing the current parity for the intersection count. Vertex 2

has a slightly different problem. The ray is inside the polygon slightly to the left of the

vertex and is inside the polygon slightly to the right. The crossing at vertex 2 should

be ignored since the ray does not transversely cross the polygon boundary. Processing

the edges separately leads to the correct result because both edges report a transverse

crossing by the ray at the common vertex 2.

The problem with the coincident polygon edge 12, 13 is that it appears as if it

is a single vertex, when viewed along the horizontal, that connects edges 11, 12 and

12, 13. If vertex 13 were to be relocated at vertex 12, the inside/outside count would

not change—the crossing at vertex 12 is transverse to the polygon boundary. At ﬁrst

glance it appears we could just ignore the edge and call the crossing transverse, but

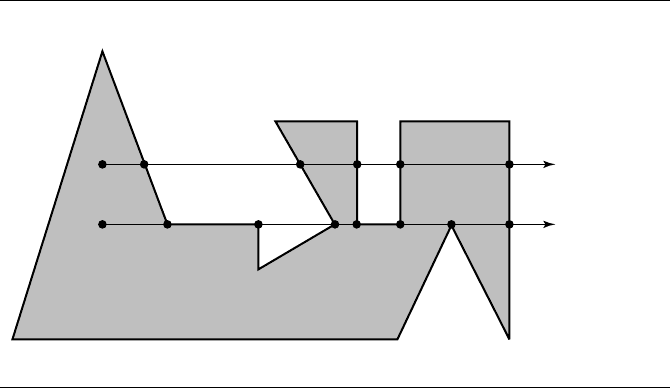
13.3 Point in Polygon 701

13 12

Figure 13.14

Point-in-polygon test by counting intersections of ray with polygon. The ray for point

only crosses edges transversely. The number of crossings is odd (5), so the point is

inside the polygon. The ray for point P

is more complex to analyze.

this is not correct. Consider the coincident edge 6, 7.Ifvertex7weretoberelocated

at vertex 6, the v-junction gets counted just like the one at vertex 2, so it is not a

transverse crossing.

Preparata and Shamos (1985) mention how to deal with these conﬁgurations.

The same idea is also mentioned by Haines (1989) and O’Rourke (1998). An edge

is counted as a crossing of the ray with the polygon if one of the end points is strictly

above the ray and the other end point is on or below the ray. Using this convention,

coincident edges are not counted as crossing edges and can be ignored. Two edges

above the ray that share a common vertex on the ray both count as crossings. If two

edges below the ray share a common vertex on the ray, neither edge is counted. If

one edge is above and one edge is below the ray, both sharing a vertex on the ray, the

edge above is counted but the edge below is not. The pseudocode for this algorithm

is listed below.

bool PointInPolygon(Point P, Polygon G)

{

bool inside = false;

for(i=0,j=G.N-1;i<G.N;j=i,i++) {

U0 = G.V(i); U1 = G.V(j);

if ((U0.y <= P.y and P.y < U1.y) // U1 is above ray, U0 is on or below ray

702 Chapter 13 Computational Geometry Topics

(U1.y <= P.y and P.y < U0.y)) // U0 is above ray, U1 is on or below ray

{

// Find x-intersection of edge with ray. Only consider edge

// crossings on the ray to the right of P.

x = U0.x + (P.y -U0.y) * (U1.x - U0.x) / (U1.y - U0.y);

if (x > P.x)

inside = not inside;

}

return inside;

}

A slight variation on the code is to compute x-P.x, combine the terms into a single

fraction, and compare to zero:

dx = ((P.y - U0.y) * (U1.x - U0.x) - (P.x - U0.x) * (U1.y - U0.y)) /(U1.y - U0.y);

if (dx > 0)

inside = not inside;

The numerator could be expanded to P.y * (U1.x - U0.x) -P.x * (U1.y - U0.y) +

(U0.x * U1.y - U1.x * U0.y)

, but this requires 4 multiplications and 5 additions. The

previous numerator requires only 2 multiplications and 5 additions. More important

is that the ﬂoating-point division is an expensive operation. The division can be

avoided by using

dy = U1.y - U0.y;

numer = ((P.y - U0.y) * (U1.x - U0.x) - (P.x - U0.x) * dy) * dy;

if (numer > 0)

inside = not inside;

or, replacing the extra multiplication by a comparison to zero,

dy = U1.y - U0.y;

numer = (P.y - U0.y) * (U1.x - U0.x) - (P.x - U0.x) * dy;

if(dy>0){

if (numer > 0) inside = not inside;

} else {

if (numer < 0) inside = not inside;

}

A ﬁnal variation takes advantage of knowing which vertex is above the ray, among

other optimizations:

13.3 Point in Polygon 703

bool PointInPolygon(Point P, Polygon G)

{

bool inside = false;

for (i = 0, j = G.N-1;i<G.N;j=i,i++) {

U0 = G.V(i); U1 = G.V(j);

if (P.y < U1.y) {

// U1 above ray

if (U0.y <= P.y) {

// U0 on or below ray

if ((P.y - U0.y) * (U1.x - U0.x) > (P.x - U0.x) * (U1.y - U0.y))

inside = not inside;

}

} else if (P.y < U0.y) {

// U1 on or below ray, U0 above ray

if ((P.y - U0.y) * (U1.x - U0.x) < (P.x - U0.x) * (U1.y - U0.y))

inside = not inside;

}

return inside;

}

The pseudocode properly classiﬁes points that are strictly inside or strictly outside

the polygon. However, points on the boundary sometimes are classiﬁed as inside,

sometimes as outside. Figure 13.15 shows a triangle and two points P and Q on

the boundary. The point P is classiﬁed as inside, the point Q is classiﬁed as outside.

Such behavior may be desirable in an application when two polygons share an edge.

A point can only be in one polygon or the other, but not both. In applications where

any edge point is required to be classiﬁed as inside, the pseudocode can be modiﬁed

to trap the case when the intersection of an edge with the ray occurs exactly at the test

point.

Let us take a closer look at the classiﬁcation issue. The reason that right edge

points are classiﬁed as outside has to do with the choice of toggling a Boolean vari-

able for inside/outside status. A different way of looking at the problem uses the line

partitioning idea in Maynard and Tavernini (1984), an unpublished work that is sum-

marized in Eberly (1999). The ideas in the work are of interest because they effectively

provide constructions that are recursive in dimension. That is, an n-dimensional

problem is reduced to solving (n − 1)-dimensional problems. Each point of intersec-

tion between an edge and a speciﬁed line is given a tag in {o, i, m, p}.Thei tag, called

the inside tag, is used if the intersection point occurs from a transverse intersection

that is interior to the edge. The m tag, called the minus tag, is used if the intersection

point is an end point of the edge, the other end point being on the negative side of

the line. Similarly, the p tag, called the plus tag, is used if the intersection point is an