Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

704 Chapter 13 Computational Geometry Topics
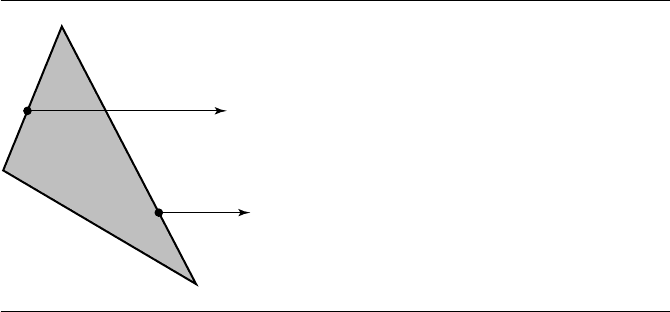
P
Q
Figure 13.15 Points P on the “left” edges of the polygon are classified as inside. Points Q on the
“right” edges of the polygon are classified as outside.
end point of the edge, the other end point being on the positive side of the line. The
o tag, called the outside tag, is used for both end points if the edge is coincident with
the line.
Each edge of the polygon is tested for intersection with the line. The first time
a point of intersection occurs, the current tag must be modified. In particular, this
happens when two or more edges share a vertex that lives on the line. The initial
tag for any point is assumed to be o. If the point occurs again and an update tag
is determined, conjunction with the old tag produces the new tag for the point.
Table 13.1 provides the update information. The rows correspond to the old tag,
the columns correspond to the update tag for the current edge, and the entry in the
appropriate row and column is the new tag. For those with a background in group
theory, you will notice that {o, i, m, p} is just the Klein-4 group where the table
indicates the group operator. The tag o is the identity element, and each element is
its own inverse.
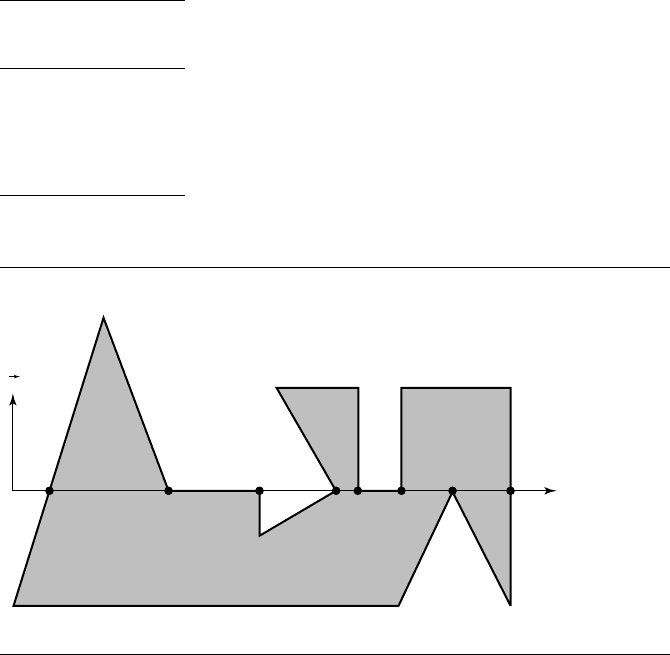
As an example, consider the polygon shown in Figure 13.14. The analysis is
applied to the ray at P
1
. The ray normal is chosen to be (0, 1). Edge 1, 2 intersects
the ray at vertex 2, and the edge is on the negative side of the ray, so the update tag for
the intersection is m. The initial tag, by default, is o.The(o, m) entry in Table 13.1 is
m, so the tag at vertex 2 is set to m. Edge 2, 3 also intersects the ray at vertex 2, and
the update tag is m since the edge is on the negative side of the ray. The new tag is
the table entry at (m, m), namely, o. Similar analysis leads to the final tags shown in
Figure 13.16. Observe that the i tag at vertex 10 occurs because the two edges sharing
that vertex have tags m and p, the table entry (m, p) being i.
The point tags are now used to label the intervals of the line partition, each
interval having a tag from {o, i, m, p}. An interval with an o tag is outside the polygon.
An interval with an i tag is inside the polygon. An interval with an m tag is coincident
13.3 Point in Polygon 705
Table 13.1
The tags for edge-line intersections are o, i, m, and p. The table is used to update the
current tag at a point of intersection. The old tag is located in the row, the update
tag for the current edge intersection is located in the column, and the new tag for the
point of intersection is the corresponding entry in that row and column.
Old Update
oi mp
ooimp
iiomp
mmpoi
ppmio
14
13 m
12
11
10
98
76
54
31
2
0
0
n
i
i
i
ppp
Figure 13.16
Point tags for the horizontal line containing P
1
in Figure 13.14.
with a polygon edge, and the interior of the polygon at that edge lies on the negative
side of the line. An interval with a p tag is coincident with a polygon edge, and the
interior of the polygon at that edge lies on the positive side of the line. The simple
yet clever idea in Maynard and Tavernini (1984) is that the vertex tags are used to
generate the interval tags using Table 13.1. The semi-infinite interval containing +∞
is clearly outside the polygon and starts with a tag of o. The left end point of that
interval is on the rightmost edge of the polygon, the point tag being i. The last interval
tag is o and is used to select the row of Table 13.1. The point tag is i and is used to
706 Chapter 13 Computational Geometry Topics
14
m
1213 10
11
985
76
4
31
2
0
ooiiiiom
n
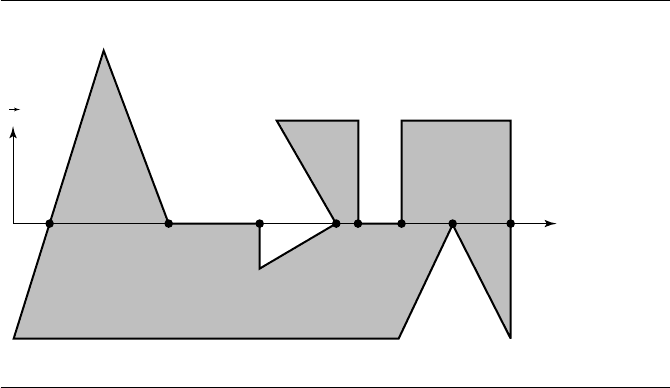
Figure 13.17
Interval tags for the horizontal line containing P
1
in Figure 13.14.
select the column of the table. The table entry (o, i) is i and becomes the tag for the
next interval. Observe that this interval is, in fact, inside the polygon. The next point
tag,atvertex2,iso. The table entry (i, o) is i, so the interval immediately to the left
of vertex 2 gets a tag of i (still inside the polygon). Figure 13.17 shows the tags for the
other intervals. Classification of P
1
is now just a matter of determining which interval
of the line partition contains the point and interpreting the label appropriately. If P
1
is
in an open interval with tag o, the point is outside the polygon. Otherwise, P
1
is inside
the polygon or on the polygon boundary. Although the tags can be constructed for
all intervals of the line, we only need the tags for the ray, so point tags to the left of P
1
need not be computed.
13.3.4 Faster Point in General Polygon
Point-in-polygon tests that are sublinear are possible, but require some type of pre-
processing of the polygon. A useful test is based on the horizontal decomposition of a
polygon into trapezoids discussed in Section 13.9. The decomposition is O(n log n),
but an intermediate data structure that is built for supporting the decomposition
allows for a point-in-polygon test in O(log n) time. A brief summary of the data
structure is given below. More details can be found in Section 13.9.
The y-values of the vertices, y
i
for 0 ≤ i<n, are used to split the polygon into
horizontal strips. The sorted y-values, denoted y
i
j
for (i
0
, ..., i
n−1
) (a permutation
of (0, ..., n − 1)), correspond to the horizontal lines that separate the strips. Each
strip itself consists of a sequence of ordered trapezoids. The polygon is the union of
13.3 Point in Polygon 707
all the trapezoids of all the strips. The sort of the y-values requires O(n log n) time,
although any particular polygon might only have a very small number of distinct
y-values. The trapezoids themselves are sorted by sorting the line segment left and
right boundaries of the trapezoids within each strip. The boundaries never overlap,
so the sort is well defined. This sort is also O(n log n) in time. The data structure
uses binary search trees to allow dynamic construction. One tree is used to sort the
horizontal strips, the other tree is used to sort the trapezoids within a strip. The
point-in-polygon test amounts to searching the first binary tree to locate the strip
containing the y-value of the input point, then searching the second binary tree to
locate the trapezoid that contains the point, if it exists. If no trapezoid is found, the
point must lie outside the polygon.
13.3.5 A Grid Method
This method is suggested by Haines in Heckbert (1994). An axis-aligned bounding
box is constructed for the polygon. A grid is imposed on the box, and the polygon is
rasterized into it. The grid cells are labeled based on their relationship to the polygon
as fully inside, fully outside, or indeterminate. The indeterminate cells are assigned
a list of edges that intersect the cell, and one corner of the cell is tagged as inside or
outside accordingly.
The grid data structure supports a constant-time point-in-polygon test when
the point occurs in a fully inside or fully outside cell. If the point occurs in an
indeterminate cell, the line segment connecting the test point and the tagged corner
is tested for intersection with all the edges in the cell’s edge list. The parity of the
number of intersections and knowing if the tagged corner is inside or outside tell you
whether or not the test point is inside or outside. This is exactly the point-in-general-
polygon test, but confined to the indeterminate cell. Because of the localization, the
number of intersection calculations is far fewer than those used in the algorithm that
counts intersections for all polygon edges. The containment test is O(1), but you pay
the price in O(nm) memory for an n × m grid and in O(nm) time to rasterize the
polygon and classify the grid cells.
Haines notes that care must be taken when a polygon edge crosses (or nearly
crosses) a grid corner. The corner is unclassifiable. Numerous options are given: deal
with the numerical precision and topological problems, regrid a slightly modified
bounding box (jittering, so to speak) in hopes that the problem goes away, or tag
entire cell edges and use the horizontal or vertical segment connecting the test point
and cell edge in the intersection counting with the edges in the cell’s edge list. If you
choose to cope with the numerical precision and topological problems, you might
as well just use the point-in-general-polygon test and deal with the same problems,
saving yourself the memory overhead and expensive preprocessing that goes with
the grid method. Regridding the bounding box is also an expensive proposition,
especially if the regridding must occur often (or worse, occurs for each test point).
708 Chapter 13 Computational Geometry Topics
The final suggestion is the most attractive in hopes that when a point falls inside an
indeterminate cell the algorithm still requires a small amount of computation time.
Regardless of how you handle the problem, the grid method can be useful in
applications such as ray tracing where the point-in-polygon test is the bottleneck, in
which case you are willing to use a lot of memory and preprocessing time to obtain
an O(1) test. But if your application is more toward the real-time end of the spectrum
and where memory is tight, the O(n) point-in-general-polygon test is your best bet.
13.4 Point in Polyhedron
A common query in graphics applications is to determine if a point is inside a polyhe-
dron. The ideas are similar to those in Section 13.3. If the polyhedron is represented
as a BSP tree, Section 13.2.3 discusses how to determine if a point is inside or outside
the polyhedron. We discuss methods here that do not assume any preprocessing of
the polyhedron.
13.4.1 Point in Tetrahedron
Consider a point P and a tetrahedron with noncoplanar vertices V
i
for 0 ≤i ≤3. To
simplify the discussions, we assume that the vertices are ordered so that the 3 × 3
matrix M whose columns are V
i
− V
0
for 0 ≤ i ≤ 2, in that order, has a positive
determinant. The canonical tetrahedron with this ordering is V
0
= (0, 0, 0), V
1
=
(1, 0, 0), V
2
= (0, 1, 0), and V
3
= (0, 0, 1). Outer-pointing normal vectors for the
triangular faces are n
0
= (V
1
− V
3
) × (V
2
− V
3
), n
1
= (V
0
− V
2
) × (V
3
− V
2
), n
2
=
(V
3
− V
1
) × (V
0
− V
1
), and n
3
= (V
2
− V
0
) × (V
1
− V
0
). The face to which n
i
is
normal is the one opposite vertex V
i
and contains the vertex V
3−i
.
The point P is inside the tetrahedron if it is on the negative side of each face plane
n
i
·(X −V
3−i
) =0. That is, P is inside the tetrahedron when n
i
·(P −V
3−i
)<0 for
all i. The point is outside the tetrahedron if n
i
· (P − V
i
)>0 for at least one i.Itis
possible that P is on the tetrahedron boundary itself, in which case n
i
·(P −V
i
) ≤0
for all i with equality for at least one i. If an equality occurs once, the point is on a
face, but not on an edge or at a vertex. If two equalities occur, the point is on an edge,
but not at a vertex. If three equalities occur, the point is at a vertex. It is not possible
for equality to occur four times.
The point can also be written in barycentric coordinates as P =
3
i=0
c
i
V
i
,where
3
i=0
c
i
= 1. P is inside the tetrahedron if 0 <c
i
< 1 for all i. The coefficient c
3
is
computed in the following manner:
P − V
0
= (c
0
− 1)V
0
+
3
i=1
c
i
V
i
=
3
i=1
c
i
(V
i
− V
0
)

13.4 Point in Polyhedron 709
so that n
3
· (P − V
0
) = c
3
n
3
· (V
3
− V
0
). Similar constructions apply for c
0
, c
1
, and
c
2
to obtain
c
0
=
n
0
· (P −V
3
)
n
0
· (V
0
− V
3
)
c
1
=
n
1
· (P −V
2
)
n
1
· (V
1
− V
2
)
c
2
=
n
2
· (P −V
1
)
n
2
· (V
2
− V
1
)
c
3
=
n
3
· (P −V
0
)
n
3
· (V
3
− V
0
)
The exact representation of P is not important for testing if it is inside the tetrahe-
dron. The denominators of the fractions are all the same negative value. The point
is inside the tetrahedron if all c
i
> 0, in which case we need all numerators to be
negative.
13.4.2 Point in Convex Polyhedron
The sidedness tests used in the point-in-tetrahedron query naturally extend to deter-
mining if a point is in a convex polyhedron. Let the faces be contained in the planes
n
i
· (X − V
i
) = 0, where V
i
is a vertex on the face and n
i
is an outer normal vector
to the face. The point P is inside the polyhedron when n
i
· (P − V
i
)<0 for all i.
The point is outside if n
i
· (P − V
i
)>0 for some i. The point is on the polyhedron
boundary itself if n
i
· (P − V
i
) ≤ 0 for all i with equality occurring for at least one
i. As in the case of the tetrahedron, if one equality occurs, the point is interior to a
face. If two equalities occur, the point is interior to an edge. If three or more equalities
occur, the point is a vertex. In this latter case, the number of equalities is the number
of faces sharing that vertex.
The algorithm is O(n),wheren is the number of vertices, since the number of
faces is also O(n). The straightforward implementation is
bool PointInPolyhedron(Point P, ConvexPolyhedron C)
{
for (i = 0; i < C.numberOfFaces; i++) {
if (Dot(C.face(i).normal, P - C.face(i).vertex) > 0)
return false;
}
return true;
}
An Asymptotically Faster Method
The index bisection method for convex polygons that supported an O(log n) query
does not apply to convex polyhedrons because of the added complexity of the third
dimension. However, a method similar to the one that bisected on the top half and
710 Chapter 13 Computational Geometry Topics
bottom half of convex polygons does extend to three dimensions, but with some
preprocessing that takes O(n) time. As such, the method is useful when many point-
in-convex-polyhedron queries must be answered.
The preprocessing consists of two steps. The first step is to iterate over the vertices
to compute the axis-aligned bounding box of the polyhedron. This box is used for
fast rejections. That is, if P is outside the bounding box, then it cannot be inside the
polyhedron. The second step is to iterate over the faces of the polyhedron. Two xy-
planar meshes of convex polygons are generated. Faces whose outer-pointing normals
have a positive z-component are projected onto one planar mesh, called the upper
planar mesh. Those with a negative z-component are projected onto the other planar
mesh, called the lower planar mesh. Faces whose normals have a zero z-component
are not relevant and can be ignored.
The two planar meshes consist of convex polygons (the polyhedron faces were
convex). Given a test point P , the (x, y) portion of the point is tested for contain-
ment in the upper planar mesh. If it is outside the mesh, then P cannot be in the
polyhedron. If it is inside the mesh, the convex polygon that contains the point must
be computed. The (x, y) portion of P must necessarily be contained in the lower pla-
nar mesh. The convex polygon in that mesh that contains P is also computed. The
line of constant (x, y) containing P intersects the polyhedral faces corresponding to
the two planar convex polygons. We now only need to determine if P is on the line
segment contained in the polyhedron—a simple task.
The technical issue is how to determine which convex polygon in a planar mesh
contains a specified point. Each edge in the mesh is shared by either one or two
polygons. Those edges shared by only one polygon form the mesh boundary—another
polygon that is itself convex since the parallel projection of a convex polyhedron onto
a plane is a convex polygon. The process of locating a point in a subdivision of the
plane implied by the mesh is called the planar point location problem.
A simple algorithm for locating the containing convex polygon is to perform a
linear walk over the mesh. An initial convex polygon is selected, and P is tested
for containment in that polygon. If so, that polygon is the containing one and the
algorithm terminates. If not, an edge of the current polygon is selected that intersects
the ray from the polygon center (computed as the average of the polygon vertices) to
P . The ray gives a general idea of which direction to walk to find P . If the ray passes
through a vertex, select either edge sharing the vertex. Once the edge has been chosen,
the next polygon to visit is the other one sharing the edge. The pseudocode is
int LinearWalk(Point P, int N, ConvexPolygon C[N])
{
index = 0;
for(i=0;i<N;i++) {
// at most N polygons to test
if (P is contained in C[index])
return index;

13.4 Point in Polyhedron 711
Point K = C[index].center; // ray origin
PointD=P-K; //raydirection
for (each edge E of C[index]) {
if (Ray(C, D) intersects E) {
index = IndexOfAdjacent(C[index], E);
break;
}
}
}
return -1; // P not in mesh, return an invalid index
}
For n polygons in the mesh, this algorithm is O(
√
n). The order is based on
intuition from a rectangular grid of size m × m. This mesh has n = m
2
rectangles. A
linear path, such as a row, column, or diagonal, contains O(m) = O(
√
n) rectangles.
The planar point location problem has an asymptotically faster solution (Kirk-
patrick 1983). The method requires building a hierarchy of nested convex polygons
and is based on the concept of independent sets of a graph. The essential result is that
the planar mesh of n vertices can be preprocessed in O(n) time and space so that
point location queries take O(log n) time. The method is not further studied here,
but is discussed in some detail by O’Rourke (1998).
13.4.3 Point in General Polyhedron
The point-in-polygon algorithm for a general polygon extends to three dimensions in
an obvious way. The polyhedron must partition space into a bounded inside region
and an unbounded outside region. A ray whose origin is the test point P and has
direction
ˆ
d = (1, 0, 0) is intersected with the faces of the polyhedron. The number
of intersections is calculated. Assuming that the ray only intersects the polyhedron
at interior face points, the parity of the number of intersections characterizes inside
from outside. If the parity is odd, the point is inside. Otherwise the parity is even and
the point is outside.
However, the same problems arise as in the 2D case when the ray intersects the
polyhedron at vertices or at interior edge points. In such a situation the parity might
be incorrectly calculated. One way to handle the problem is based on using the vertex-
edge-face table that represents the polyhedron. The algorithm performs an iteration
over the faces of the polyhedron. Each processed face is tagged that it was visited. If
the ray intersects a face at an interior edge point, the adjacent face that shares the edge
is immediately tagged as visited so that when it is visited later in the iteration, it is not
tested for intersection. Moreover, the parity will have to be adjusted based on the local
configuration of the ray, the common edge, and the faces sharing that edge. Figure
13.18 shows the two relevant configurations. Determining the local configuration is
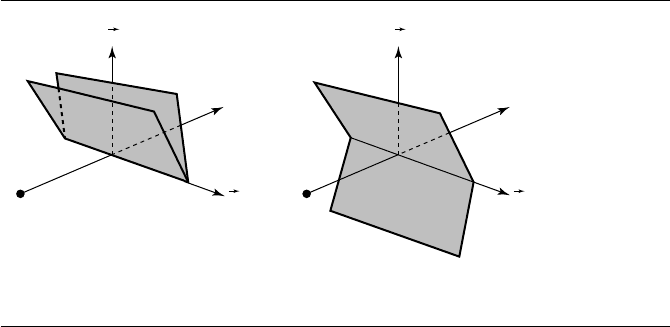
712 Chapter 13 Computational Geometry Topics
PP
(a) (b)
n
e e
ˆ
n
d
ˆ
d
Figure 13.18 Two configurations for when the test ray P + t
ˆ
d intersects a shared edge e at an
interior edge point. (a) The faces are on the same side of the plane formed by the
edge and the ray. Parity is not changed. (b) The faces are on opposite sides. Parity is
toggled.
a simple task of selecting two vertices, one from each face but not on the common
edge, and computing on which side of the ray-edge plane they lie. The ray-intersects-
edge situation in 3D is the analogy of the ray-intersects-vertex situation in 2D.
If the ray intersects a vertex V , the situation is more complicated and does not
have a counterpart in the 2D setting. The problem is to decide if the ray penetrates
the polyhedron at V or if it just grazes the vertex so that locally the ray remains in
the same region. Specifically, let V = P + t
0
ˆ
d for some parameter t
0
. For a suitably
small >0, we need to determine if the two open line segments (line segments
not including their end points) corresponding to parameter intervals (t
0
− , t
0
) and
(t
0
, t
0
+ ) are both inside or both outside, in which case the current parity is not
changed, or one is inside and one is outside, in which case the current parity is
toggled. We can imagine a very “ruffled” vertex whose adjacent faces form a triangle
strip that wanders aimlessly through space locally at the vertex, perhaps making the
problem appear to be intractable. However, the saving fact is that a polyhedron is a
manifold mesh (see Section 9.3.3). If a unit sphere is centered at V and the edges
sharing V are rescaled to be unit length, the corresponding spherical points form a
simple closed curve on the sphere, more precisely a piecewise-defined curve whose
pieces are great circle arcs. The interior region bounded by that curve corresponds to
the interior of the polyhedron at V . The ray direction itself can be normalized and
corresponds to a point on the sphere. The ray interpenetrates the polyhedron at V
if and only if the corresponding sphere point is inside the spherical polygon implied
by the edges sharing V . (See Figure 13.19.) This is not quite the point-in-polygon
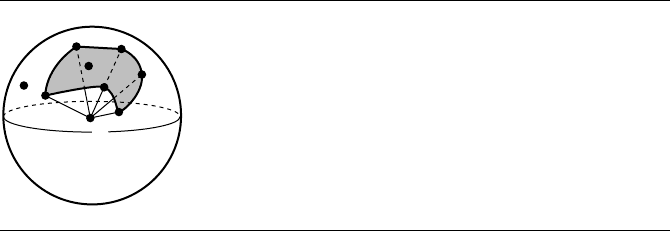
13.4 Point in Polyhedron 713
B
A
V
Figure 13.19 The spherical polygon implied by the edges sharing a vertex V that the test ray
intersects. If the point A corresponds to the ray direction, the ray interpenetrates
the polyhedron. If the point B corresponds to the ray direction, the ray does not
interpenetrate the polyhedron.
test discussed earlier, but a similar algorithm to the one for planar polygons can be
constructed for spherical polygons.
An alternative to the fine-scale handling is to use a randomized approach. The
idea is to generate random directions until a ray is found that only intersects faces at
interior points. The pseudocode is
bool PointInPolyhedron(Point P, ConvexPolyhedron C)
{
parity = false;
i=0;
while (i < C.numberOfFaces) {
Point D = GenerateRandomUnitVector();
for (i = 0; i < C.numberOfFaces; i++) {
if (Ray(P, D) intersects C.face(i)) {
if (intersection point is interior to face))
parity = not parity;
else // bad ray, try a different one
break;
}
}
}
return parity;
}
