Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

714 Chapter 13 Computational Geometry Topics
Although it is expected that eventually the outer loop terminates, it is not clear
how many iterations will occur until then. A variation is to replace the
while loop
by a
for loop that runs at most a specified number of iterations. If a good ray is not
found for all those iterations, a call can be made to a much slower algorithm, for
example the algorithm in Paeth (1995), “Point in Polyhedron Testing Using Spherical
Polygons.” This method requires computing solid angles, operations that use inverse
trigonometric function calls, hence the slower performance.
13.5 Boolean Operations on Polygons
A common question that arises in computer graphics is how to compute the in-
tersection of two polygons A and B, a query that is one of a collection of queries
generally known as Boolean operations on polygons. Each polygon is assumed to be
non-self-intersecting in that no edge transversely crosses another edge, but edges
meeting at vertices are allowed. Usually each polygon is assumed to enclose a con-
nected, bounded region that possibly has holes. We do not require boundedness and
allow edges to be line segments, rays, or lines. We also do not require connectedness.
For example, two disjoint triangles may be considered to be part of a single polygon.
The generality of the definition for polygon allows for operations other than inter-
section to be implemented in a fairly simple way.
The plane must be partitioned by the polygon into two disjoint regions, an inside
region and an outside region. Each linear component of the (potentially unbounded)
polygon has a normal vector associated with it. The region to which the normal is
directed is labeled the “outside;” the opposite region is labeled as “inside.” Equiva-
lently, if the linear components are represented as having directions, as you traverse
the component in the specified direction the inside region is to your left and the out-
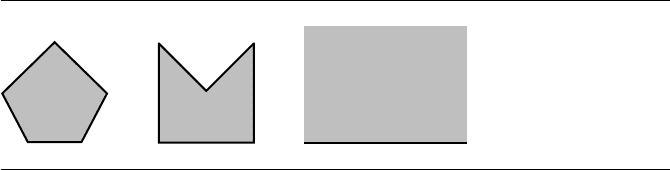
side region is to your right. Figure 13.20 illustrates with three polygons, one bounded
and convex, one bounded and not convex, and one unbounded.
Figure 13.20 Bounded and unbounded polygons that partition the plane into inside and outside
regions. The inside region is gray. The unbounded polygon on the right is a half-space
with a single line as the boundary of the region.
13.5 Boolean Operations on Polygons 715
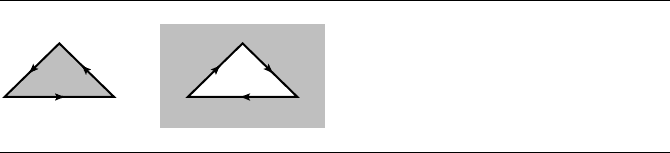
Figure 13.21 A polygon and its negation. The inside regions are gray. The edges are shown with
the appropriate directions so that the inside is always to the left.
13.5.1 The Abstract Operations
The Boolean operations on polygons include the following operations.
Negation
This operation reverses the labeling of the inside and outside regions. The inside
region becomes the outside region, and the outside region becomes the inside region.
If the polygon is stored so that the normals for the edges are explicitly stored, then
negation is implemented as a sign change on the normals. If the polygon is stored so
that the edges are directed, then negation is implemented by reversing the directions
of all edges. Figure 13.21 shows a polygon and its negation.
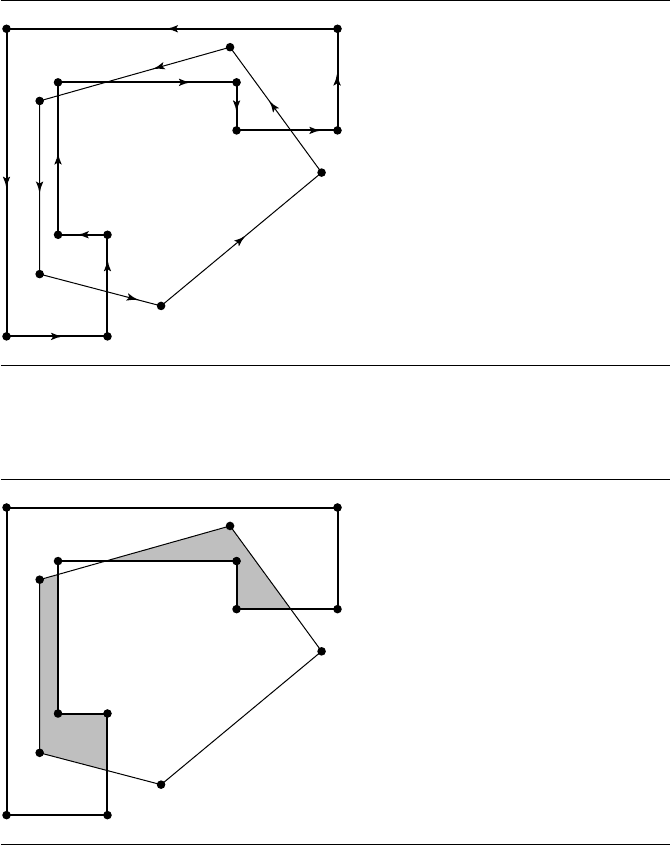
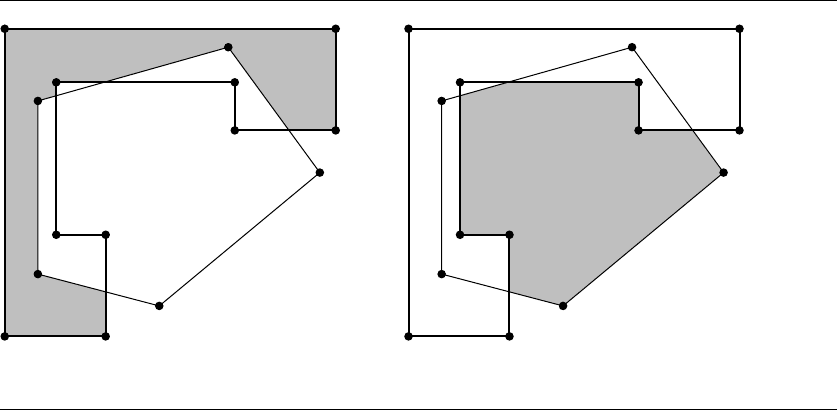
The remaining operations will be illustrated with the two polygons shown in
Figure 13.22, an inverted L-shaped polygon and a pentagon. The edge directions are
shown, indicating that the inside regions for both polygons are bounded.
Intersection
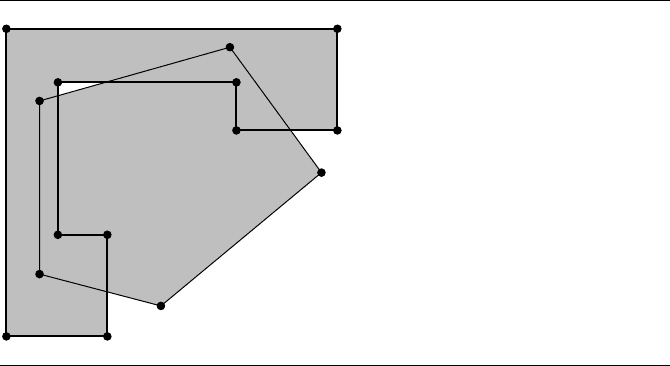
The intersection of two polygons is another polygon whose inside region is the inter-
section of the inside regions of the initial polygons. Figure 13.23 shows the intersec-
tion of two polygons. The polygon vertices and edges are black, and the intersection
is gray. The intersection is a polygon according to our definition mentioned at the
beginning of this section, and it consists of two components, each a simple polygon.
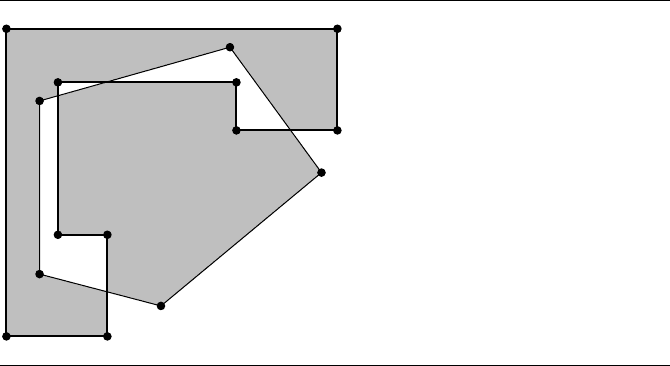
Union
The union of two polygons is another polygon whose inside region is the union of the
inside regions of the initial polygons. Figure 13.24 shows the union of two polygons.
The polygon vertices and edges are black, and the union is gray.
716 Chapter 13 Computational Geometry Topics
Figure 13.22 Two polygons whose inside regions are bounded.
Figure 13.23
The intersection of two polygons shown in gray.
13.5 Boolean Operations on Polygons 717
Figure 13.24 The union of two polygons shown in gray.
Difference
The difference of two polygons is another polygon whose inside region is the dif-
ference of the inside regions of the initial polygons. The order of the polygons is
important. If A is the set of points for the inside of the first polygon and B is the
set of points for the inside of the second polygon, then the difference A \ B is the set
of points that are in A, but not in B. Figure 13.25 shows the difference of the two
polygons, the inverted L-shaped polygon minus the pentagon. The polygon vertices
and edges are black, and the difference is gray.
Exclusive-Or
The exclusive-or of two polygons is another polygon whose inside region is the union
of the two polygon differences. If A is the inside region for the first polygon and B is
the inside region for the second polygon, then the inside region for the exclusive-or
is the set (A \B) ∪(B \A). Figure 13.26 shows the exclusive-or of the two polygons.
The polygon vertices and edges are black, and the exclusive-or is gray.
13.5.2 The Two Primitive Operations
Although the Boolean operations can be implemented according to each of the set op-
erations as defined, it is only necessary to implement negation and intersection. The
other Boolean operations can be defined in terms of these two primitive operations.
718 Chapter 13 Computational Geometry Topics
(b)(a)
Figure 13.25 The difference of two polygons: (a) The inverted L-shaped polygon minus the pentagon.
(b) The pentagon minus the inverted L-shaped polygon.
Negation
ThenegationofpolygonP is denoted ¬P . This unary operator has precedence over
any of the following binary operators.
Intersection
The intersection of polygons P and Q is denoted P ∩ Q.
Union
The union of polygons P and Q is denoted P ∪ Q and can be computed using De
Morgan’s rules for sets by
P ∪ Q =¬(¬P ∩¬Q)
13.5 Boolean Operations on Polygons 719
Figure 13.26 The exclusive-or of two polygons shown in gray. This polygon is the union of the two
differences shown in Figure 13.25.
Difference
The difference of polygons P and Q,whereQ is subtracted from P , is denoted P \Q
and can be computed by
P \ Q = P ∩¬Q
Exclusive-Or
The exclusive-or of polygons P and Q is denoted P ⊕ Q = (P \Q) ∪ (Q \ P) and
can be computed by
P ⊕ Q =¬((¬(P ∩¬Q)) ∩ (¬(Q ∩¬P )))
13.5.3 Boolean Operations Using BSP Trees
Various approaches have been taken for computing Boolean operations on polygons.
A popular method that is straightforward to implement uses BSP trees. The ideas
extend in a natural way to three dimensions where the Boolean operations are applied
to polyhedra (see Section 13.6). The two primitive operations are discussed below.
720 Chapter 13 Computational Geometry Topics
Negation
The polygon negation operation is simple to implement. Assuming the polygon data
structure stores edges, as is the case in the discussion of BSP tree representations for
polygons, negation is implemented by reversing the ordering for each edge.
Polygon Negation(Polygon P)
{
Polygon negateP;
negateP.vertices = P.vertices;
for (each edge E of P) do
negateP.Insert(Edge(E.V(1), E.V(0)));
return negateP;
}
The BSP tree that represents the polygon is negated using the following pseu-
docode:
BspTree Negation(BspTree T)
{
BspTree negateT = new BspTree;
for (each edge E of T.coincident)
negateT.coincident.Insert(Edge(E.V(1), E.V(0)));
if (T.posChild)
negateT.negChild = Negation(T.posChild);
else
negateT.negChild = null;
if (T.negChild)
negateT.posChild = Negation(T.negChild);
else
negateT.negChild = null;
return negateT;
}
Intersection
The intersection of polygons can be computed in a straightforward manner. If A and
B are polygons, each edge of A is intersected with B. Any portions of those edges that
lie inside B are retained as part of the polygon of intersection. Similarly, each edge of
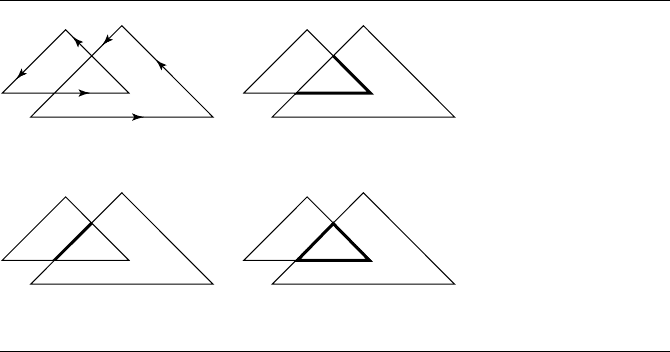
13.5 Boolean Operations on Polygons 721
(a) (b)
(c) (d)
AB
Figure 13.27 Intersection of two triangles: (a) The two triangles, A and B. (b) Edges of A inter-
sected with inside of B. (c) Edges of B intersected with inside of A. (d) A ∩ B as the
collection of all intersected edges.
B is intersected with A, and any portions of those edges that lie inside A are retained
as part of the polygon of intersection. Figure 13.27 illustrates this. Although a simple
algorithm, the problem is that it is not as efficient as it could be. If polygon A has n
edges and polygon B has m edges, then the number of edge-edge intersection tests is
nm, so the algorithm has O(nm) time complexity (quadratic in time). The use of BSP
trees reduces the number of comparisons since edges of A on one side of a splitting
line need not be compared to edges of B on the other side.
As illustrated in Figure 13.27, the edges of each polygon must be intersected with
the inside region of the other polygon. Any subedges that are inside become part of
the intersection of the two polygons.
The pseudocode is
Polygon Intersection(Polygon P, Polygon Q)
{
Polygon intersectPQ;
for (each edge E of P) {
GetPartition(E, Q, inside, outside, coincidentSame, coincidentDiff);
for (each S in (inside or coincidentSame))
intersectPQ.Add(S);
}
for (each edge E of Q) {
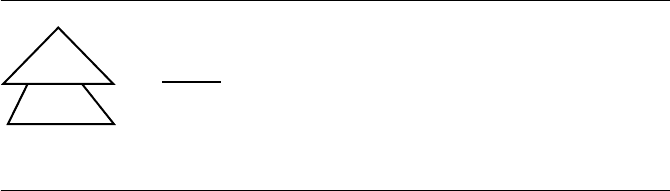
722 Chapter 13 Computational Geometry Topics
GetPartition(E, P, inside, outside, coincidentSame, coincidentDiff);
for (each S in (inside or coincidentSame))
intersectPQ.Add(S);
}
return intersectPQ;
}
The heart of the construction is partitioning an edge E of a polygon by intersecting
it with the other polygon. The function
GetPartition constructs four sets of segments
of an edge
E intersected with the specified polygon, at least one set being nonempty.
Two sets correspond to segments inside the polygon or outside the polygon. The other
two sets correspond to segments that are coincident with an edge of the polygon, one
set storing those segments that are in the same direction as an edge (
coincidentSame),
the other set storing segments in the opposite direction (
coincidentDiff). As dis-
cussed in Section 13.1.4, the partitioning is performed efficiently using a BSP tree
representation of the polygon by the BSP tree function
GetPartition.
The decision not to include coincident segments in the opposite direction of
the corresponding polygon’s edge has the consequence that intersection finding only
computes intersections with positive area. For example, Figure 13.28 shows two poly-
gons whose intersection is a line segment. The pseudocode for intersection shown
earlier will report that the polygons do not intersect. You can, of course, include the
other set of coincident edges if you want the intersector to return a line segment in
this example. A slightly more complicated example is shown in Figure 13.29. The
pseudocode, as listed, returns the triangle portion of the intersection but not the ex-
tra edge hanging off that triangle. If you modify the code to include all coincident
segments, the intersector returns the triangle and the extra edge. Some applications
might require the true set of intersection; others might only want the components of
intersection with positive area. The implementation should handle this as needed.
The intersection operation as discussed here supports what are called keyhole
edges, two edges that are collinear but have opposite direction. Keyhole edges are
A
B
(a) (b)
Figure 13.28
(a) Two polygons that are reported not to intersect by the pseudocode. (b) The actual
set intersection, a line segment.
13.5 Boolean Operations on Polygons 723
(a) (b)
A
B
Figure 13.29 (a) Two polygons and (b) their true set of intersection.
(a) (b)
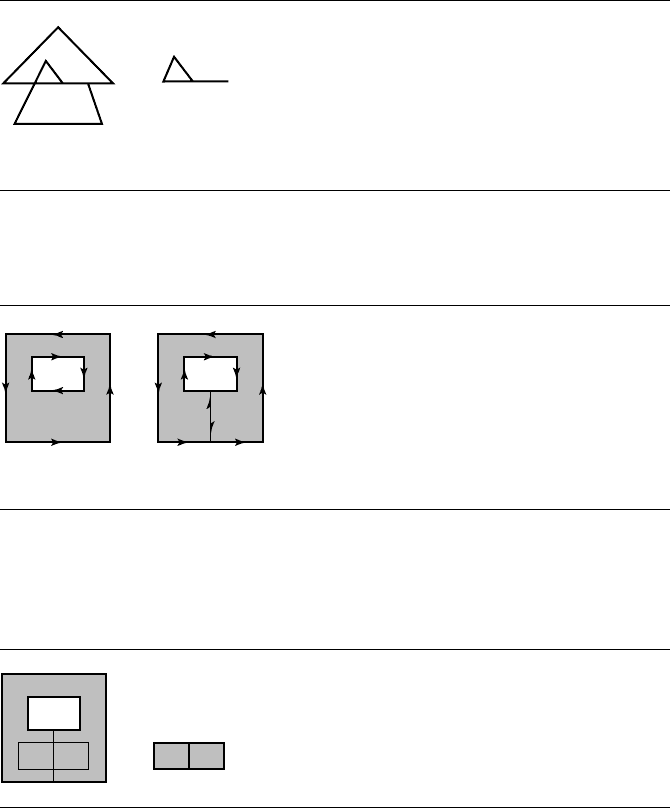
Figure 13.30
(a) Polygon with a hole requiring two lists of vertices/edges. (b) Keyhole version to
allow a single list of vertices/edges.
Figure 13.31 Intersection of a rectangle and a keyhole polygon.
typically used to represent polygons with holes in terms of a single collection of
vertices/edges. Figure 13.30 shows a polygon with a hole and a keyhole representa-
tion of it. However, be aware that the intersection of a polygon with a keyhole polygon
might be theoretically a simple polygon, but constructed as a union of multiple sim-
ple polygons. Figure 13.31 illustrates the intersection of a rectangle with the keyhole
polygon of the previous figure. The intersection set contains two adjacent but oppo-
site direction edges that could be removed by a postprocessing step.
