Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

724 Chapter 13 Computational Geometry Topics
Other Boolean Operations
Using negation and intersection as the primitive operations, the remaining Boolean
operations are implemented below.
Polygon Union(Polygon P, Polygon Q)
{
return Negation(Intersection(Negation(P), Negation(Q)));
}
Polygon Difference(Polygon P, Polygon Q)
{
return Intersection(P, Negation(Q));
}
Polygon ExclusiveOr(Polygon P, Polygon Q)
{
return Union(Difference(P, Q), Difference(Q, P));
}
As mentioned earlier, the overhead of assembling the intersection from an edge
list may lead to poor performance. An alternative would be to start with the edge
lists and BSP trees from the original polygons and not create intermediate polygons,
only the final polygon. A simple improvement for the exclusive-or operation is to use
instead a binary operator
DisjointUnion operation whose vertices are the union of
the vertices of the two input polygons and whose edges are the union of the edges of
the two input polygons. The two difference polygons have no edges in common, so a
full-fledged
Union operation does more work than it has to in this special case.
13.5.4 Other Algorithms
The BSP tree-based algorithm is not the only possibility for implementing Boolean
polygon operations, in particular intersection of polygons. All methods have one
thing in common—they must find points of intersection between pairs of edges. The
edges on which the intersection points occur must be split (in an abstract sense) into
subedges. What varies among the methods is how the subedges are merged to form
the intersection polygon.
We briefly mention some alternatives. The Weiler-Atherton (WA) algorithm
(Weiler and Atherton 1977) is one whose implementation is requested frequently in
the computer graphics newsgroups. A detailed description, including how the data
structures are designed, is in Foley et al. (1996). However, the next two algorithms
are, in our opinion, better choices for reasons shown below. An algorithm based
on sweep lines (sorting vertices by one component) is attributed to Sechrest and
13.5 Boolean Operations on Polygons 725
Greenberg (1981) and referred to here as the SG algorithm. A slightly modified SG
algorithm is attributed to Vatti (1992) and referred to as the V algorithm. The latter
algorithm allows the output of an intersection of polygons to be a collection of trape-
zoids rather than a general polygon, something that is useful for point-in-polygon
tests. The flavor of the V algorithm is present in the horizontal decomposition of a
polygon into trapezoids that is discussed in Section 13.9.
Performance in computing edge-edge intersections is important. The obvious
algorithm that checks all possible pairs is certainly the most inefficient. The BSP
algorithm avoids comparing all pairs of edges just by nature of the spatial sorting
implied by the splitting lines. The WA algorithm checks all possible pairs. The SG
and V algorithms provide the most efficient testing because of the horizontal sorting
that occurs by using a sweep line approach.
The process of identifying subedges for the intersection polygon is a natural con-
sequence of the BSP algorithm. Moreover, this algorithm inherently provides a con-
vex decomposition of the intersection polygon. However, the general decomposition
comes at the cost of more edge comparisons than in the SG and V algorithms. The
subedge identification and merging in the WA algorithm is accomplished by doubling
the edges. Each abstract polygon edge has two instantiations, one that is assigned to
the inside of the polygon and one that is assigned to the outside. Labels on those
edges are maintained that store this information. Intersection points for edge pairs
are located, and the edges containing the point are split (all four of them). The edges
are reconnected based on the labels to form nonintersecting contours, one of which
corresponds to the intersection polygon. The subedge identification and merging in
the SG and V algorithms is based on the partitioning of the polygon into horizon-
tal strips, each strip containing a list of trapezoids in the strip. Again, the material in
Section 13.9 gives greater detail on the partitioning.
The concern for any algorithm that computes the intersection of polygons is what
types of polygons it will handle. All methods assume some consistent ordering of
the polygon vertices, whether it be clockwise or counterclockwise. Does the method
only handle convex polygons? Will it handle polygons with holes, or more gener-
ally, nested polygons? Will it allow polygons with self-intersecting edges? How does
the method handle coincident edges? Some methods claim “correct” handling of co-
incident edges, but as seen in Figures 13.28 and 13.29, the choice of behavior for
coincident edges is application-specific. An application might very well only want
intersection polygons that have positive area. In theory, all the algorithms discussed
here can handle nested polygons, but specific implementations might not.
Implementations of the various algorithms are available online. Klamer Schutte
has one based on the WA algorithm, but with some modifications to the merge of
subedges into the intersection polygon (Schutte 1995). This implementation requires
clockwise ordering of vertices, does not support holes, and does not support self-
intersecting polygons.
Michael Leonov has an implementation that is a modification of the one by
Schutte, but allows for holes (Leonov 1997). The outer polygon must be counter-
clockwise ordered, and the inner polygons forming holes must be clockwise ordered.
726 Chapter 13 Computational Geometry Topics
Leonov also had, at one point, a very nice comparison of various implementations in-
cluding an analysis of execution times to determine order of convergence and a chart
indicating whether or not the implementations could handle various classes of poly-
gons. Unfortunately as of the time of printing of this book, that page appears to no
longer be available.
Alan Murtha has an implementation based on the V algorithm and appears to be
well written and quite popular for downloading (Murtha 2000). Klaas Holwerda also
has an implementation based on the V algorithm (Holwerda 2000).
Two implementations are available through the source code pages at Eberly
(2001), one using the concept of polysolids and one using BSP trees.
13.6 Boolean Operations on Polyhedra
This topic is considered to be part of a general class of methods, collectively called
computational solid geometry (CSG), that operate on 3D objects. The concepts for
Boolean operations on polyhedra are identical to those for operations on polygons.
We recommend reading Section 13.5 first to understand how Boolean operations
apply to polygons. The polyhedra are assumed to partition space so that the abstract
graph of regions is 2-colorable. Intuitively, each disjoint region is labeled as “inside”
or “outside” the polyhedron. Generally, the inside regions are bounded (have finite
volume), but the more general term “2-colorable” is used to allow both inside and
outside regions to be unbounded. For example, a half-space is allowed in the Boolean
operations. The outside region is labeled based on selecting a plane normal to point
to that side of the plane. The inside region is on the other side. Polyhedra that provide
a 2-coloring of space and for which the inside region is bounded have been referred
to as polysolids in the context of CSG (Maynard and Tavernini 1984).
13.6.1 Abstract Operations
The abstract operations include negation of a polyhedron, which reverses the labels
on inside and outside regions; intersection of two polyhedra, the subpolyhedra that
are contained by both input polyhedra; union of two polyhedra, the polyhedra that
are contained by either input polyhedron; difference of two polyhedra, the polyhedra
that are contained in the first input polyhedron, but not in the second; and exclusive-
or of two polyhedra, the union of the differences of the two polyhedra. Just as in
the two-dimensional setting, negation and intersection are primitive operations. The
other operations are expressed in terms of them. Negation of a polyhedron P is
denoted ¬P , and intersection of polyhedra P and Q is denoted P ∩ Q. The union
is P ∪ Q =¬(¬P ∩¬Q), the difference is P \ Q = P ∩¬Q, and the exclusive-
or is P ⊕ Q =¬((¬(P ∩¬Q)) ∩ (¬(Q ∩¬P ))). A minimal coding of Boolean
operations involves implementing negation and intersection, then constructing the
other operations according to these identities.
13.6 Boolean Operations on Polyhedra 727
13.6.2 Boolean Operations Using BSP Trees
The use of BSP trees is quite effective for implementing Boolean operations for
polyhedra. The ideas can be found in Thibault and Naylor (1987); Naylor (1990);
Naylor, Amanatides, and Thibault (1990); and Naylor (1992). The discussion in this
section assumes that the polyhedra are stored in a vertex-edge-face table and that the
face vertices are ordered so that the face normals correspond to a counterclockwise
orientation of the vertices. The normals are assumed to point to the outside region.
Negation
The polyhedron negation is simple in that the vertex ordering for the faces is reversed
and normals, if stored, have their directions reversed by multiplying by −1. The
pseudocode is
Polyhedron Negation(Polyhedron P)
{
Polyhedron negateP;
negateP.vertices = P.vertices;
negateP.edges = P.edges;
for (each face F of P) {
Face F’;
for (i = 0; i < F.numVertices; i++)
F’.InsertIndex(F.numVertices-i-1);
negateP.faces.Insert(F’);
}
return negateP;
}
The BSP tree that represents the polyhedron is negated using the following pseu-
docode:
BspTree Negation(BspTree T)
{
BspTree negateT = new BspTree;
for (each face F of T.coincident) {
Face F’;
for (i = 0; i < F.numVertices; i++)
F’.InsertIndex(F.numVertices-i-1);
negateT.coincident.Insert(F’);
}
728 Chapter 13 Computational Geometry Topics
if (T.posChild)
negateT.negChild = Negation(T.posChild);
else
negateT.negChild = null;
if (T.negChild)
negateT.posChild = Negation(T.negChild);
else
negateT.negChild = null;
return negateT;
}
Intersection
The intersection of polyhedra is also computed in a straightforward manner. If A
and B are polyhedra, each face of A is intersected with B. Any portions of those
faces that lie inside B are retained as part of the polyhedron of intersection. Similarly,
each face of B is intersected with A, and any portions of those faces that lie inside A
are retained as part of the polyhedron of intersection. Just as in the two-dimensional
setting, the O(nm) algorithm that tests pairs of faces, each pair having one face from
the n faces of A and one face from the m faces of B, is inefficient. The use of BSP trees
reduces the number of comparisons because of the spatial sorting that is implied by
the tree.
The pseudocode is listed below:
Polyhedron Intersection(Polyhedron P, Polyhedron Q)
{
Polyhedron intersectPQ;
for (each face F of P) {
GetPartition(Q.bsptree, F, inside, outside, coinside, cooutside);
for (each face S in (inside or coinside))
intersectPQ.faces.Insert(S);
}
for (each face F of Q) {
GetPartition(P.bsptree, F, inside, outside, coinside, cooutside);
for (each face S in (inside or coinside))
intersectPQ.faces.Insert(S):
}
}
13.7 Convex Hulls 729
The heart of the construction is partitioning a face F of a polyhedron by intersect-
ing it with the other polyhedron. The function that does this is
GetPartition, the one
discussed in Section 13.2.5.
Other Boolean Operations
The remainder of the Boolean operations use the identities discussed earlier.
Polyhedron Union(Polyhedron P, Polyhedron Q)
{
return Negation(Intersection(Negation(P), Negation(Q)));
}
Polyhedron Difference(Polyhedron P, Polyhedron Q)
{
return Intersection(P, Negation(Q));
}
Polyhedron ExclusiveOr(Polyhedron P, Polyhedron Q)
{
return Union(Difference(P, Q), Difference(Q, P));
}
13.7 Convex Hulls
AsetS ⊂R
n
is said to be convex if for any X, Y ∈S, the line segment (1 −t)X +tY ∈
S for all t ∈ [0, 1]. This definition does not require the set to be bounded or to be
closed. For example, all of R
2
is convex. The half-plane in R
2
defined by x>0is
convex. Other examples of convex sets are circular disks and triangles. Of course,
lines, rays, and line segments are all convex. Figure 13.32 shows two sets: the set in
Figure 13.32(a) is convex, but the set in Figure 13.32(b) is not. In 3D, examples of
convex sets are R
3
, half-spaces, spheres, ellipsoids, lines, rays, line segments, triangles,
and tetrahedra.
The convex hull ofasetS is the smallest convex set that contains S. Of particular
interest in computer graphics is the convex hull of a finite set of points. This section
focuses on the construction of convex hulls for point sets.
13.7.1 Convex Hulls in 2D
Consider a finite point set S. If all points in the set are collinear, the convex hull is a
line segment. The more interesting case is when at least three points are not collinear.
730 Chapter 13 Computational Geometry Topics
(a) (b)
P
Q
Figure 13.32 (a) Convex. (b) Not convex, since the line segment connecting P and Q is not entirely
inside the original set.
Figure 13.33 A point set and its convex hull. The points are in dark gray, except for those points
that became hull vertices, marked in black. The hull is shown in light gray.
In this case the convex hull is a region bounded by a polygon that is denoted a convex
polygon. Figure 13.33 shows a point set and its convex hull. The vertices of the convex
hull are necessarily a subset of the original point set. Construction of the convex hull
amounts to identifying the points in S that are the vertices of the convex polygon.
Numerous algorithms have been developed for computing the convex hull of
point sets. A summary of these is found in O’Rourke (1998) and includes gift
wrapping, quickhull, Graham’s algorithm, incremental construction, and a divide-
and-conquer method. We only discuss the last two algorithms in the list. Various
computational geometry books make restrictions on the point sets in order to sim-
plify the constructions and proofs. Typical assumptions include no duplicate points,
no collinear points, and/or points have only integer coordinates to allow exact arith-
metic. In practice, these restrictions are usually never satisfied, especially in the
presence of a floating-point number system. We pay close attention to the patho-
logical problems that can arise in order to provide a robust implementation.
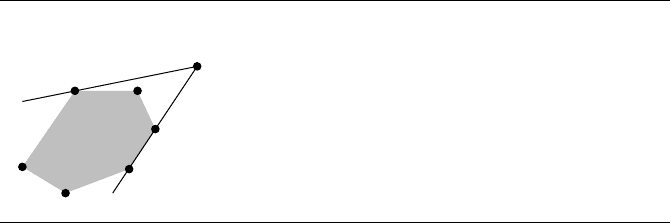
13.7 Convex Hulls 731
Upper
tangent
Lower
tangent
V
A
B
H
P'
L
P
L
P
U
Figure 13.34 AconvexhullH ,apointV outside H , and the two tangents from V to the hull. The
upper and lower tangent points are labeled as P
U
and P
L
, respectively.
Incremental Construction
The idea is simple. Given a set of points V
i
,0≤ i<n, each point is inserted into an
already constructed convex hull of the previous points. The pseudocode is
ConvexPolygon IncrementalHull(int n, Point V[n])
{
ConvexPolygon hull = {V[0]};
for(i=1;i<n;i++)
Merge(V[i], hull);
return hull;
}
The heart of the problem is how to construct the convex hull of a convex polygon
H and a point V , the operation named
Merge in the pseudocode. If V is inside H ,
the merge step does nothing. But if V is outside H , the merge step must find rays
emanating from V that just touch the hull. These rays are called tangents to the hull
(see Figure 13.34).
A tangent has the property that the hull is entirely on one side of the line with
at most a vertex or an edge of points on the line. In Figure 13.34, the upper tangent
intersects the current hull in a single point. The lower tangent intersects along an
edge of the current hull. The points of tangency are the extreme points of all the hull
vertices that are visible from V . The other hull vertices are occluded from V by the
hull itself. In the figure, the lower tangent contains an edge with end points P
L
and
P
L
, but only P
L
is visible to V .
The condition of visibility from V can be further exploited. The current hull edges
inside the cone defined by the two tangents are visible to V . These edges are inside
the new hull containing H and V . The new hull includes all the occluded edges of the
current hull and new edges formed by the line segments from V to the tangent points.
In the example of Figure 13.34, two edges are visible to V and can be discarded. The
732 Chapter 13 Computational Geometry Topics
new edges are V , P
U
and V , P
L
. Because the edge P
L
, P
L
is entirely on the lower
tangent, that edge can also be discarded and replaced by the new edge V , P
L
. If this
step is not performed, the final hull of the points will contain collinear edges. Such
edges can be collapsed in a postprocessing phase.
Determining whether or not an edge is visible is just a matter of computing or-
dering of three points, the end points of the directed edge and the point V . In Figure
13.34, the directed edge P
L
, A is visible to V . The triangle V , P
L
, A is clock-
wise ordered. The directed edge P
U
, B is not visible to V . The triangle V , P
U
, B
is counterclockwise ordered. Only P
L
of the directed edge P
L
, P
L
is visible to V .
The triangle V , P
L
, P
L
is degenerate (a line segment). The cases are quantified by
a dot product test. Let Q
0
, Q
1
be a directed hull edge and define
d = Q
1
− Q
0
and
n =−
d
⊥
, an inner-pointing normal to the edge. The edge is visible to V whenever
n ·(V − Q
0
)<0 and not visible to V whenever n · (V − Q
0
)>0. If the dot product
is zero, then only the closest end point of the edge is visible to V . End point Q
0
is
closest if
d · (V − Q
0
)<0; end point Q
1
is closest if
d · (V − Q
0
)>
d
2
.
The order of the algorithm depends on the amount of work that must be done
in the merge step. In the worst case, each input point to
Merge is outside the current
hull, and the tangent points are found by iterating over all hull vertices and testing
the dot product conditions. The order is O(n
2
). Because of this, one hope is that the
initial points are ordered in such a way that most of the time the input point is in
the current hull. This is the idea of randomized algorithms, where the input points are
randomly permuted in an attempt to generate a large partial hull from the first few
input points. When this happens, many of the remaining points most likely will fall
inside the current hull. Because the relationship between the next input point and
the current hull is not known, a search over the hull vertices must be made to find
the tangent points. A randomized algorithm is discussed in de Berg et al. (2000). The
same idea occurs in Section 13.11 when finding the minimum-area circle containing
a point set.
A nonrandomized approach that guarantees an O(n log n) algorithm actually
sorts the points so that the next input point is outside the current hull! The sort
of the points dominates the algorithm time. The points are sorted using the less-
than operation: (x
0
, y
0
)<(x
1
, y
1
) when x
0
<x
1
or when x
0
= x
1
and y
0
<y
1
.The
points are initially sorted in place for the discussion. In an implementation, the points
are most likely sorted into separate storage so as not to change the original point
set. After the sort, duplicate points can be eliminated. The sort and comparison can
be implemented to use fuzzy floating-point arithmetic to handle those cases where
floating-point round-off errors might cause two equal points (in theory) to be slightly
different from each other.
The algorithm has information about the relationship between the next input and
the current hull so that the tangent construction is only O(n) over the total lifetime of
the loop in the pseudocode. In particular, the last-inserted hull vertex is the starting
point for the search for the points of tangency and may already be a tangent point
itself. Although any single search might require visiting a significant number of points
13.7 Convex Hulls 733
on the current hull, each such visited point will be interior to the merged hull and
discarded. The average cost per discarded point is effectively constant time, so over
the lifetime of the loop, the total time is O(n).
The first point is the initial hull. As input points are processed, a flag,
type,is
maintained that indicates whether the hull is a single point (
POINT), a line segment
represented by two distinct points (
LINEAR), or a convex polygon with positive area
(
PLANAR). Initially the flag is POINT since the initial point stored by the hull is the first
input point. By keeping track of this flag, we effectively have a convex hull algorithm
for a given dimensional space (in this case 2D) that is based on convex hull algorithms
for the spaces of smaller dimension (in this case 1D). The pseudocode becomes
ConvexPolygon IncrementalHull(int n, Point V[n])
{
Sort(n, V);
RemoveDuplicates(n, V); // n can decrease, V has contiguous elements
ConvexPolygon hull;
type = POINT;
hull[0] = V[0];
for(i=1;i<n;i++) {
switch (type) {
case POINT: type = LINEAR; hull[1] = V[i]; break;
case LINEAR: MergeLinear(V[i], hull, type); break;
case PLANAR: MergePlanar(V[i], hull); break;
}
}
return hull;
}
If the current hull has one point, the uniqueness of the points implies that V[i]
is different from the one already in the hull. The point is added to the current hull to
form a line segment and the
type flag is changed accordingly.
If the current hull has two points (a line segment), the function
MergeLinear
determines whether or not the current input point is on the same line as the line
segment. If it is on the same line, the current hull is updated and remains a line
segment. If the input point is not on the same line, the current hull and input
point form a triangle. In this case, the triangle is stored as the current hull and
the
type flag is changed accordingly. Moreover, we wish to store the hull as a set
of counterclockwise-ordered points. This requires the collinearity test to do slightly
more than just determine if the input point is on or off the line. If the hull is the line
segment Q
0
, Q
1
and the input point is P , Figure 13.35 shows the five possibilities
for the relationship of P to the line segment.
The collinearity test uses a normal vector to the line containing the segment
Q
0
, Q
1
.If
d = Q
1
− Q
0
, then n =−
d
⊥
, a normal vector that points to the left as
