Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

734 Chapter 13 Computational Geometry Topics

(a) (b)

Figure 13.35 The ﬁve possibilities for the relationship of P to a line segment with end points Q

and Q

: P is (a) to the left of the segment, (b) to the right of the segment, (c) on the

line to the left of the segment, (d) on the line to the right of the segment, or (e) on

the line and contained by the segment.

you traverse the segment from Q

to Q

. Deﬁne a =P −Q

. The ﬁve possibilities,

labeled according to Figure 13.35, are characterized mathematically by

a. n ·a>0

b. n ·a<0

c. n ·a =0 and



d ·a<0

d. n ·a =0 and



d ·a>



d ·



e. n ·a =0 and 0 ≤



d ·a ≤



d ·



The pseudocode uses an integer ﬂag to distinguish between these cases, the val-

ues given in the order of the tests above as

POSITIVE, NEGATIVE, COLLINEAR_LEFT,

COLLINEAR_RIGHT, and COLLINEAR_CONTAIN.

13.7 Convex Hulls 735

int CollinearTest(Point P, Point Q0, Point Q1)

{

PointD=Q1-Q0,N=-Perp(D),A=P-Q0;

float NdA = Dot(N, A);

if (NdA > 0)

return POSITIVE;

if (NdA < 0)

return NEGATIVE;

float DdA = Dot(D, A);

if (DdA < 0)

return COLLINEAR_LEFT;

if (DdA > Dot(D, D))

return COLLINEAR_RIGHT;

return COLLINEAR_CONTAIN;

}

Observe that the ﬁve possibilities match exactly those discussed for visibility of

vertices and edges for the current hull from the input point V . The pseudocode for

merging is listed below. If the hull becomes a triangle, the vertices are arranged in

counterclockwise order.

void MergeLinear(Point P, ConvexPolygon& hull, int& type)

{

switch (CollinearTest(P, hull[0], hull[1])) {

case POSITIVE:

type = PLANAR;

hull = {P, hull[0], hull[1]};

break;

case NEGATIVE:

type = PLANAR;

hull = {P, hull[1], hull[0]};

break;

case COLLINEAR_LEFT:

// collinear order <P, Q0, Q1>

hull = {P, Q1};

break;

case COLLINEAR_RIGHT:

// collinear order <Q0, Q1, P>

hull = {Q0, P};

break;

736 Chapter 13 Computational Geometry Topics

case COLLINEAR_CONTAIN:

// collinear order <Q0, P, Q1>, hull does not change

break;

}

Although theoretically correct, CollinearTest suffers from the usual problems

with ﬂoating-point round-off error. Points can be nearly collinear, but may as well

be treated as if they were collinear. A robust application would instead use fuzzy

arithmetic for the collinear test. Relative error tolerances should be used to avoid

dependencies on the magnitude of the input points. One possibility is to use an error

threshold ε>0 on the cosine of the angle θ between



d and a.If| cos(θ )|≤ε, then θ

may as well be treated as zero. That is, if |n ·a|=na| cos(θ)|≤εna, then

the three points are treated as collinear. The lengths of two vectors must be computed

in this formulation, a performance issue. To avoid the square root calculations, the

squared equation should be considered instead, |n ·a|

≤ εn

a

, where we are

using ε as a tolerance on | cos(θ)|

. A similar error threshold can be used for the

case when the three points are collinear. The parametric interval of containment is

[0, 



d

], but can be expanded to [−ε



d

, (1 + ε)



d

]. The pseudocode to handle

this is listed below where

epsilon0 and epsilon1 are deﬁned to be whatever the

application writer deems appropriate.

int CollinearTest(Point P, Point Q0, Point Q1)

{

PointD=Q1-Q0,A=P-Q0;

float NdA = D.x * A.y - D.y * A.x; // N = -Perp(D) = (-D.y, D.x)

float NdN = D.x * D.x + D.y * D.y; // |N| = |D|

float AdA = A.x * A.x + A.y * A.y;

if (NdA * NdA > epsilon0 * NdN * AdA) {

if (NdA > 0)

return POSITIVE;

if (NdA < 0)

return NEGATIVE;

}

float DdA = Dot(D, A);

if (DdA < -epsilon1 * NdN)

return COLLINEAR_LEFT;

if (DdA > (1 + epsilon1) * NdN)

return COLLINEAR_RIGHT;

return COLLINEAR_CONTAIN;

}

13.7 Convex Hulls 737

Once the current hull has three or more points, it is guaranteed to remain a

convex polygon with positive area regardless of the values of any further input points.

The ﬁnal function to discuss is

MergePlanar. Once the ﬁrst triangle, if any, is

created by

MergeLinear, the last inserted point that led to the triangle is always stored

hull[0]. This point is a good candidate for searching for the tangent points formed

by the next input point and the current hull. The planar merge contains two loops,

one to ﬁnd the upper tangent point and one to ﬁnd the lower tangent point. The loop

bodies just test for visibility based on the results of

CollinearTest applied to the input

point and edges of the current hull. The pseudocode is

void MergePlanar(Point P, ConvexPolygon& hull)

{

// find upper tangent point

for(U=0;i=1;U<hull.N;U=i,i=(i+1)modhull.N) {

test = CollinearTest(P, hull[U], hull[i]);

if (test == NEGATIVE) // edge visible, go to next edge

continue;

if (test == POSITIVE // edge not visible,

|| test == COLLINEAR_LEFT) { // only edge end point is visible

// upper found

break;

}

// test == COLLINEAR_CONTAIN || test == COLLINEAR_RIGHT

// Theoretically cannot occur when input points are distinct and

// sorted, but can occur because of floating-point round-off

// when P is very close to the current hull. Assume P is on the

// hull polygon--nothing to do.

return;

}

// find lower tangent point

for (L = 0; i = hull.N - 1; i >= 0;L=i,i--) {

test = CollinearTest(P, hull[i], hull[L]);

if (test == NEGATIVE) // edge visible, go to next edge

continue;

if (test == POSITIVE // edge not visible,

|| test == COLLINEAR_RIGHT) { // only edge end point is visible

// lower found

break;

}

738 Chapter 13 Computational Geometry Topics

// test == COLLINEAR_CONTAIN || test == COLLINEAR_LEFT

// Theoretically cannot occur when input points are distinct and

// sorted, but can occur because of floating-point round-off

// when P is very close to the current hull. Assume P is on the

// hull polygon--nothing to do.

return;

}

// Both tangent points found. Now do:

// 1. Remove visible edges from current hull.

// 2. Add new edges formed by P and tangent points.

}

The simplest algorithm for updating the hull in steps 1 and 2 indicated in the

pseudocode is to create a temporary hull from the current hull and input point by

iteration:

ConvexPolygon tmpHull;

tmpHull[0] = P;

for (i = 1; true; i++,U=(U+1)modhull.N) {

tmpHull[i] = hull[U];

if (U == L)

break;

}

hull = tmpHull;

However, the iteration is O(n), so the incremental algorithm becomes O(n

).To

avoid this, it is important to maintain the hull as some type of linked structure so

that the linked chain of visible edges can be disconnected at the tangent points, an

O(1) operation, and deletion needs to be done in O(1) time. The chain should not be

deleted one node at a time; otherwise you are back to O(n) time. This requires an

implementation that pays close attention to memory management. After the linked

chain is removed, new links are added from the node representing P to the nodes

representing the tangent points.

An important note about the architecture of the algorithm is in order. All of the

problems due to ﬂoating-point round-off errors are encapsulated by the function

CollinearTest. Any unexpected results from an application of the incremental hull

algorithm can only be due to the implementation of

CollinearTest, particularly in

the choice of the relative error thresholds ε

and ε

. The encapsulation makes it easy

to debug any problems that arise in the application.

13.7 Convex Hulls 739

Divide-and-Conquer Method

A standard paradigm in computer science is divide and conquer. The idea is to take

a problem, divide it into two smaller problems of the same type, solve the smaller

problems, and merge the results to construct the solution to the original problem. If

the problem has n inputs and T

is the time it takes to solve the problem, the division

into two smaller problems, each with half the inputs, leads to the recursion formula

= 2T

n/2

+ M

. Each smaller problem has (approximately) n/2 inputs and takes

n/2

time to solve (by deﬁnition of T

). The quantity M

represents the time it takes

to merge the solution to the two smaller problems. If M

takes linear time, O(n),

then it can be shown that the solution T

is O(n log n). Recurrences of this form are

discussed in detail in Cormen, Leiserson, and Rivest (1990). The divide-and-conquer

method applied to convex hulls turns out to have a linear-time merge, so the convex

hull algorithm for a set of n points takes O(n log n) time.

As in the incremental construction of the convex hull, the input points are sorted

according to the same scheme: (x

, y

)<(x

, y

) when x

or when x

= x

and

. We also make no assumptions about the structure of the point set. Just as

in the incremental hull algorithm, the input points are sorted and duplicates are

removed. The initial pseudocode is

ConvexPolygon DividAndConquerHull(int n, Point V[n])

{

Sort(n, V);

RemoveDuplicates(n, V); // n can decrease, V has contiguous elements

ConvexPolygon hull;

GetHull(0,n-1,V,hull);

return hull;

}

The recursive construction occurs in GetHull. Its structure is shown below. The

values

i0 and i1 are the ﬁrst and last indices of a subset of points whose convex hull

must be computed.

void GetHull(int i0, int i1, Point V[], ConvexPolygon& hull)

{

int quantity = i1 - i0 + 1;

if (quantity > 1) {

// middle index of input range

int mid = (i0 + i1) / 2;

// find hull of subsets (mid - i0+1>=i1-mid)

ConvexPolygon LHull, RHull;

GetHull(i0, mid, V, LHull);

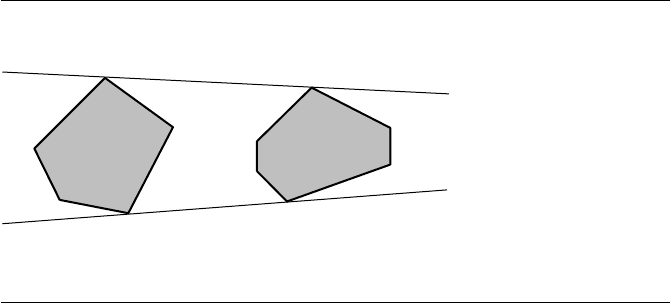
740 Chapter 13 Computational Geometry Topics

Upper tangent

Lower tangent

Figure 13.36 TwoconvexhullsH

and H

and their upper and lower tangents.

GetHull(mid + 1, i1, V, RHull);

// merge the convex hulls into a single convex hull

Merge(LHull, RHull, hull);

} else {

// convex hull is a single point

hull[0] = V[i0];

}

The technical problem, of course, is how Merge computes the convex hull of two

convex hulls. The idea is an extension of that for computing the convex hull of a

single point, a convex set itself, and a convex polygon. In the latter case, the merge

depended on ﬁnding upper and lower tangents to the hull and containing the single

point; Figure 13.34 shows the typical situation. For two convex polygons, we still must

ﬁnd upper and lower tangents to both hulls; Figure 13.36 shows the typical situation.

Unlike the incremental hull problem, we do not know one of the tangent points ahead

of time. An exhaustive search over pairs of points, one from each polygon, results

in an O(n

) merge. An O(n) merge is readily available instead if we perform the

following walking algorithm on the left hull H

and the right hull H

The method is described for ﬁnding the lower tangent to the hulls. Find the point

on H

with the largest x-component, a linear-time process. Find the point Q

with the smallest x-component, also linear time. If the line containing P

and Q

is not tangent to H

, traverse the vertices of H

in the clockwise direction (decrement

i) until the line is tangent to H

. Now switch to H

. If the line containing the current

and Q

is not tangent to H

, traverse the vertices of H

in the counterclockwise

direction (increment j) until the line is tangent to H

. This traversal produces a new

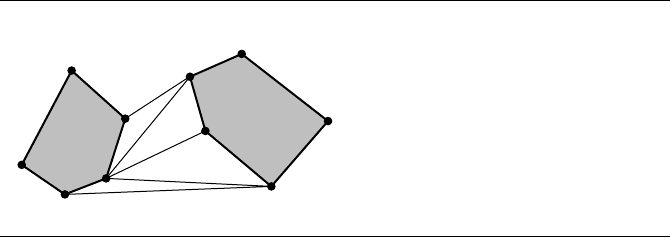
13.7 Convex Hulls 741

Figure 13.37

TwoconvexhullsH

and H

and the incremental search for the lower tangent.

line that might no longer be tangent to H

. Alternately repeat the traversals until

the line is tangent to both hulls. Figure 13.37 shows a typical situation. The extreme

points are P

and Q

. The initial segment, labeled 1, is P

, Q

. This segment is not

tangent to the left hull at P

, so the left hull index is decremented (modulo 5), and

the new segment, labeled 2, is P

, Q

. This segment is tangent to the left hull at

, but it is not tangent to the right hull at Q

. The right hull index is incremented,

and the new segment, labeled 3, is P

, Q

. The segment is not tangent to the right

hull, so the right hull index is incremented again, and the new segment, labeled 4,

is P

, Q

. The segment is now tangent to the right hull, but not tangent to the left

hull. The left hull index is decremented, and the new segment, labeled 5, is P

, Q

.

This segment is tangent to both hulls and is the lower tangent to the hull. It is possible

that a tangent is collinear with a hull edge that shares the tangent point, but rather

than test for this in each merge and extend the tangent to include the collinear edge

if necessary, removal of collinear edges can be done as a postprocess on the convex

polygon returned by the hull construction.

The pseudocode for

Merge is listed below. The case of small sets near the leaf nodes

of the implicit binary tree implied by the recursion are specially handled.

void Merge(ConvexPolygon LHull, ConvexPolygon RHull, ConvexPolygon& hull)

{

if (LHull.n == 1 && RHull.n == 1) {

// duplicate points were removed earlier, the hull is a line segment

hull[0] = LHull[0];

hull[1] = RHull[0];

return;

}

if (LHull.n == 1 && RHull.n == 2) {

// merge point and line segment, result in RHull

MergeLinear(LHull[0], RHull);

hull = RHull;

742 Chapter 13 Computational Geometry Topics

return;

}

if (LHull.n == 2 && RHull.n == 1) {

// merge point and line segment, result in LHull

MergeLinear(RHull[0], LHull);

hull = LHull;

return;

}

if (LHull.n == 2 && RHull.n == 2) {

// merge point and line segment, result in LHull

MergeLinear(RHull[1], LHull);

if (LHull.n == 2) {

// RHull[1] was on line of LHull, merge next point

MergeLinear(RHull[0], LHull);

hull = LHull;

return;

}

// RHull[1] and LHull form a triangle. Remove RHull[1] so that

// RHull is a single point. LHull has been modified to be a

// triangle. Let the tangent search take care of the merge.

RHull.Remove(1);

}

// find indices of extreme points with respect to x

LMax = IndexOfMaximum{LHull[i].x};

RMin = IndexOfMinimum{RHull[i].x};

// get lower tangent to hulls, start search at extreme points

LLIndex = LMax; // lower left index

LRIndex = RMin; // lower right index

GetTangent(LHull, RHull, LLIndex, LRIndex);

// get upper tangent to hulls, start search at extreme points

ULIndex = LMax; // upper left index

URIndex = RMin; // upper right index

GetTangent(RHull, LHull, URIndex, ULIndex);

// construct the counterclockwise-ordered merged-hull vertices

ConvexPolygon tmpHull;

i=0;

for (each j between LRIndex and URIndex inclusive) {

tmpHull[i] = hull[j];

i++;

13.7 Convex Hulls 743

}

for (each j between ULIndex and LLIndex inclusive) {

tmpHull[i] = hull[j];

i++;

}

hull = tmpHull;

}

The function MergeLinear has identical structure to the one used in the incremen-

tal hull construction, with the minor change in semantics that the input line segment

polygon is modiﬁed to store the merged hull.

The tangent search uses the same concepts of visibility as in the incremental hull

construction. As described earlier, the search ﬂip-ﬂops between the two input hulls.

The input indices

L and U are the starting ones for the search. On return, the indices

correspond to the tangent points on the two hulls.

void GetTangent(ConvexPolygon LHull, ConvexPolygon RHull, int& L, int& R)

{

// In theory the loop terminates in a finite number of steps, but the

// upper bound for the loop variable is used to trap problems caused by

// floating-point round-off errors that might lead to an infinite loop.

for(inti=0;i<LHull.n + RHull.n; i++) {

// end points of potential tangent

Point L1 = LHull[L];

Point R0 = RHull[R];

// walk clockwise along left hull to find tangency

int Lm1 = (L - 1) mod LHull.n;

Point L0 = LHull[Lm1];

int test = CollinearTest(R0, L0, L1);

if (test == NEGATIVE || test == COLLINEAR_LEFT) {

L = Lm1;

continue;

}

// walk counterclockwise along right hull to find tangency

int Rp1 = (R + 1) mod RHull.n;

Point R1 = RHull[Rp1];

test = CollinearTest(L1, R0, R1);

if (test == NEGATIVE || test == COLLINEAR_RIGHT) {

R = Rp1;

continue;

}