Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

754 Chapter 13 Computational Geometry Topics

and the triangles of the convex polyhedron are added to the table. The

Hull<3> data

structure represents points as (s

, s

). On the reformatting, these values become

, s

,0) to be in the same space as (t

, t

). All such 4-vectors are coordinates

in the afﬁne system with origin A and basis vectors

, and

The

Update function ﬁnds the terminator of the hull, in this case the simple, closed

polyline that separates the visible faces from the hidden ones. The faces visible to P

are removed, and new faces formed by P and the terminator edges are added to the

hull.

Finally, the hyperspatial merge is shown below. Because the original space has

dimension 4, there is no need to project out the basis components since the corre-

sponding vector r (

R in the pseudocode) will always be



void Merge<4>(Point P, Hull<4> hull)

{

// Uses affine coordinate system {A; D1, D2, D3}.

// Hull remains hyperspatial.

B=P-A;

t1 = Dot(D1, B);

t2 = Dot(D2, B);

t3 = Dot(D3, B);

t4 = Dot(D4, B);

Update(hull, t1, t2, t3, t4);

}

The Update function ﬁnds the terminator of the hull, the collection of faces that

separate the visible hyperfaces from the hidden ones. The hyperfaces visible to P are

removed, and new hyperfaces formed by P and the terminator faces are added to

the hull. Since the last routine works on 4-vectors, the afﬁne coordinates are not

necessary, and the points can be manipulated in the original coordinate system.

If this choice is made in an implementation, then the block of code in

Merge<3>

for the increase in dimension to 4 can be appended with code to replace all the

points (stored in afﬁne coordinates) in the current hull with the original points. This

requires storing the original indices of the input points, but this is something that is

done in small-dimension implementations anyway because the indices for the input

data set should be used to store connectivity information, not the indices of the sorted

data set. Also if this choice is made, then

Merge<4> just calls the update function.

If the general format of a merge function is preserved by doing the projection

anyway, we can implement a single, generic merge function, as shown below.

void Merge<k>(Point P, Hull<k> hull)

{

B=P-A;

R=B;

for (i = 1; i <= k; i++) {

13.7 Convex Hulls 755

t[i] = Dot(D[i], B);

R=R-t[i] * D[i];

}

if (|R| > 0) {

// dimension increases

h=h+1;

convert hull from Hull<k> format to Hull<k + 1> format;

D[k+1]=R/|R|;

t[k + 1] = Dot(D[k + 1], B);

ReformatAndInsert<k + 1>(hull,t ); // t = (t[1],...,t[k + 1])

} else {

// hull remains the same dimension

Update<k>(hull, t); // t = (t[1],...,t[k])

}

To keep the implementation simple, the Update<k> function can be written to just

iterate over all hyperfaces and keep those that are hidden and remove those that are

visible, all the while keeping track of each face that is shared by a visible hyperface

and a hidden hyperface, then iterate over those faces and form the hyperfaces with P

and add them to ﬁnalize the merged hull.

The ﬂoating-point issues in this approach are threefold. First, the computation

of the afﬁne coordinates

t[i] will involve ﬂoating-point round-off errors. Second,

the comparison of length of r to zero should be replaced by a comparison to a

small, positive threshold. Even so, such a comparison is affected by the magnitude

of the inputs. Third, the

Update function tests for visibility of hyperfaces. Each test

is effectively a (k + 1) × (k + 1) determinant calculation where the ﬁrst row of the

matrix has all 1 entries and the columns, not including the ﬁrst row entries, are the

points forming the hyperface and the input point. Floating-point round-off errors

may cause incorrect classiﬁcation when the determinant is theoretically nearly zero.

Divide-and-Conquer Method

The basic concept is the same as in small dimensions. The important function is

Merge, which computes the convex hull of two other convex hulls. Although easy

to describe, the implementation is quite difﬁcult to build. A supporting hyperplane

must be found for the two hulls. A hyperedge that is not part of either hull is used

to fold the hyperplane until it encounters a vertex of either hull. That vertex and the

hyperedge are used to form a hyperface of the merged hull. The wrapping continues

until the original hyperedge is encountered. The hyperfaces visible to either of the

input hulls must be removed. As in the 3D problem, the set of such hyperfaces on a

single hull is connected, so a depth-ﬁrst search sufﬁces to ﬁnd and remove them. The

hidden hyperfaces on each input hull are, of course, kept for the merged hull.

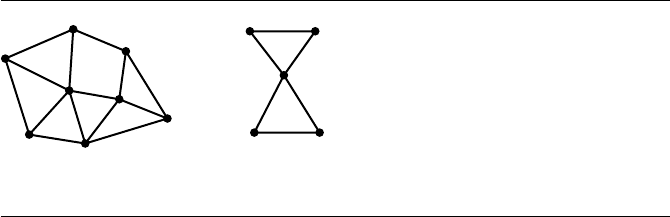
756 Chapter 13 Computational Geometry Topics

(a) (b)

Figure 13.42

Triangulations of ﬁnite point sets: (a) with optional requirements; (b) without.

13.8 Delaunay Triangulation

A triangulation of a ﬁnite set of points S ⊂ R

is a set of triangles whose vertices

are the points in S and whose edges connect pairs of points in S.EachpointofS is

required to occur in at least one triangle. The edges are only allowed to intersect at the

vertices. An optional requirement is that the union of the triangles is the convex hull

of S. Figure 13.42 shows triangulations of two point sets. The triangulation in Figure

13.42(a) includes the optional requirement, but the triangulation in Figure 13.42(b)

does not. Similar terminology is used for constructing tetrahedra whose vertices are

points in a ﬁnite set S ⊂R

. The computational geometry researchers also refer to this

as a triangulation, but some practitioners call this a tetrahedralization.ForS ⊂R

,an

object whose vertices are in S is called a simplex (plural simplices), the generalization

of triangle and tetrahedron to higher dimensions. We suppose that simplexiﬁcation is

as good a term as any for constructing the simplices whose vertices are in S.

A common desire in a triangulation is that there not be long, thin triangles. Con-

sider the case of four points forming a convex quadrilateral. Figure 13.43 shows the

two different choices for triangulation where the vertices are (±2, 0) and (0, ±1).The

goal is to select the triangulation that maximizes the minimum angle. The triangula-

tion in Figure 13.43(b) has this property. The concept of maximizing the minimum

angle produces a Delaunay triangulation. A better formal development is presented in

computational geometry books and is based on understanding Voronoi diagrams for

ﬁnite point sets and constructing the Delaunay triangulation from it. An important

concept is that of a circumcircle, the circle containing the three vertices of a triangle.

Although the angles of the triangles can be computed explicitly, the choice of one

of the two triangulations is equivalently determined by containment of one point

within the circumcircle of the other three points. In Figure 13.44, (0, −1) is inside

the circumcircle of triangle (2, 0), (0, 1), (−2, 0), but (−2, 0) is outside the circum-

circle of triangle (2, 0), (0, 1), (0, −1). The Delaunay triangulation has the property

that the circumcircle of each triangle contains no other points of the input set. This

property is used for incremental construction of the triangulation, the topic discussed

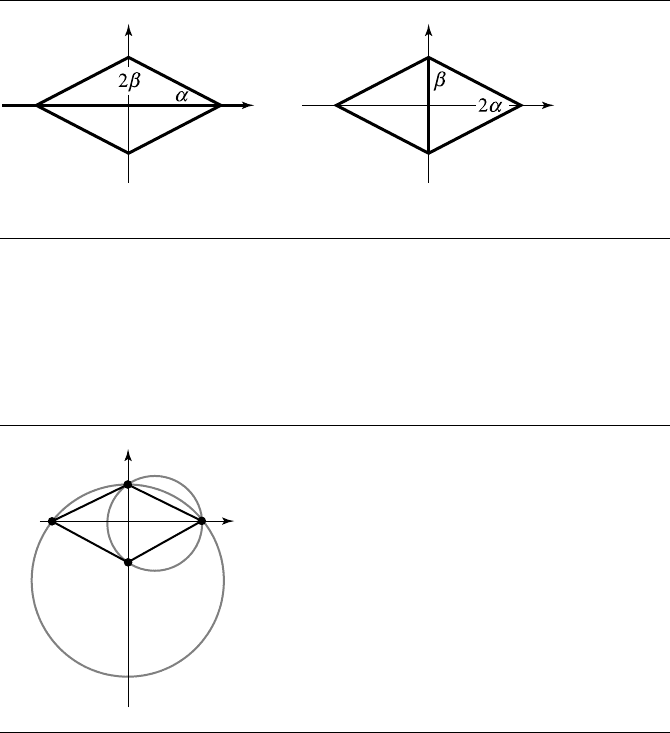
13.8 Delaunay Triangulation 757

2–2

–1

2–2

–1

(a) (b)

Figure 13.43

The two triangulations for a convex quadrilateral. The angle α

0.46 radians and the

angle β

1.11 radians. (a) The minimum angle of the top triangle is α (smaller than

β). (b) The minimum angle is 2α radians (smaller than β); the triangles maximize

the minimum angle.

(–2, 0) (2, 0)

(0, 1)

(0, –1)

Figure 13.44 Two circumcircles for the triangles of Figure 13.43.

next. The original ideas of constructing the triangulation incrementally are found in

Bowyer (1981) and Watson (1981).

13.8.1 Incremental Construction in 2D

Given a ﬁnite set of points in R

, the triangulation begins by constructing a triangle

large enough to contain the point set. As it turns out, it should be large enough to also

contain the union of circumcircles for the ﬁnal triangulation. The triangle is called a

supertriangle for the point set. There are inﬁnitely many supertriangles. For example,

758 Chapter 13 Computational Geometry Topics

if you have one supertriangle, then any triangle containing it is also a supertriangle.

A reasonably sized triangle that is easy to compute is one that contains a circle that

contains the axis-aligned bounding rectangle of the points.

Each input point P is inserted into the triangulation. A triangle containing P

must be found. An iteration over all triangles and point-in-triangle tests clearly al-

low you to ﬁnd a triangle, but this can be a slow process when the input set has a

large number of points. A better search uses a linear walk over the current triangles.

This type of search was presented in Section 13.4.2 for a mesh of convex polygons.

The idea, of course, specializes to the case when the polygons are all triangles. Two

possible situations happen as shown in Figure 13.45. If P is interior to a triangle T ,

that triangle is split into three subtriangles, N

for 0 ≤ i ≤ 2. Before the split, the

invariant of the algorithm is that each pair T , A

,whereA

is an adjacent trian-

gle to T , satisﬁed the empty circumcircle condition. That is, the circumcircle of T

did not contain the opposite vertex of A, and the circumcircle of A did not con-

tain the opposite vertex of T . After the split, T will be removed, so the triangles A

are now adjacent to the new triangles N

. The circumcircle condition for the pairs

N

, A

 might not be satisﬁed, so the pairs need to be processed to make sure the

condition is satisﬁed by a swap of the shared edge, the type of operation illustrated in

Figure 13.43.

The pseudocode for the incremental construction is listed below:

void IncrementalDelaunay2D(int N, Point P[N])

{

mesh.Insert(Supertriangle(N, P)); // mesh vertices V(0), V(1), V(2)

for(i=0;i<N;i++) {

C = mesh.Container(P[i]); // triangle or edge

if (C is a triangle T) {

// P[i] splits T into three subtriangles

for(j=0;j<3;j++) {

// insert subtriangle into mesh

N = mesh.Insert(i, T.v(j), T.v(j + 1));

// N and adjacent triangle might need edge swap

A = T.adj(j);

if (A is not null)

stack.push(N, A);

}

mesh.Remove(T);

} else {

// C is an edge E

// P[i] splits each triangle sharing E into two subtriangles

for (k = 0; k <= 1; k++) {

T = E.adj(k);

13.8 Delaunay Triangulation 759

if (T is not null) {

for(j=0;j<3;j++) {

if (T.edge(i) is not equal to E) {

// insert subtriangle into mesh

N = mesh.Insert(i, T.v(j), T.v(j + 1));

// N and adjacent triangle might need edge swap

A = T.adj(j);

if (A is not null)

stack.push(N, A);

}

mesh.Remove(T);

}

// Relevant triangles containing P[i] have been subdivided. Now

// process pairs of triangles that might need an edge swapped to

// preserve the empty circumcircle constraint.

while (stack is not empty) {

stack.pop(T, A);

// see Figure 13.45 to understand these indices

compute i0, i1, i2, i3 with T.v(i1)= A.v(i2) and T.v(i2)= A.v(i1);

if (T.v(i0) is in Circumcircle(A)) {

// swap must occur

N0 = mesh.Insert(T.v(i0), T.v(i1), A.v(i3));

B0 = A.adj(i1);

if (B0 is not null)

stack.push(N0, B0); now <N0,B 0> might need swapping

N1 = mesh.Insert(T.v(i0), A.v(i3), A.v(i2));

B1 = A.adj(i3);

if (B1 is not null)

stack.push(N1, B1); now <N1, B1> might need swapping

}

// remove any triangles that share a vertex from the supertriangle

mesh.RemoveTrianglesSharing(V(0), V(1), V(2));

}

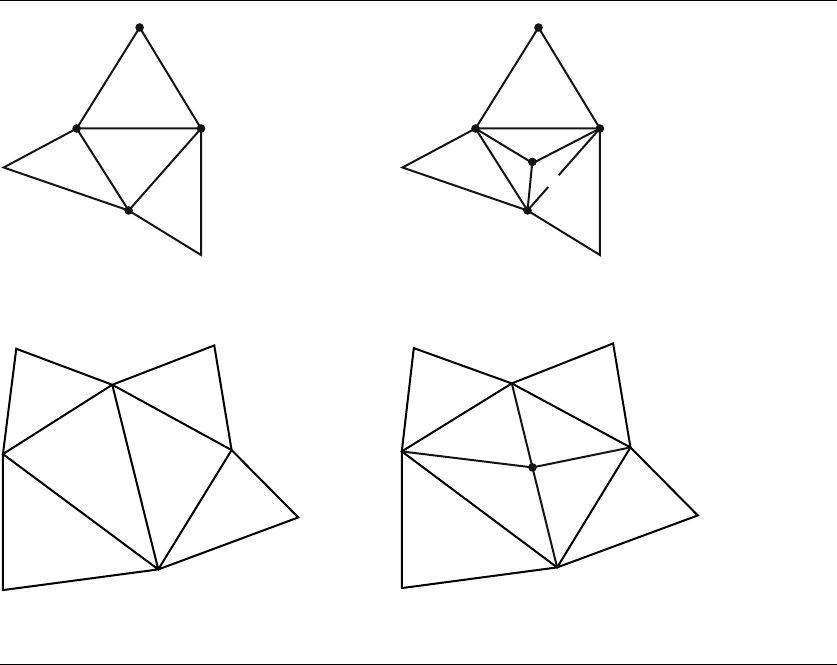
760 Chapter 13 Computational Geometry Topics

(a)

(b)

Figure 13.45 (a) The newly inserted point P , shown as an unlabeled black dot, is interior to a triangle,

in which case the triangle is split into three subtriangles, or (b) it is on an edge of a

triangle, in which case each triangle sharing the edge (if any) is split into two subtriangles.

The function

Supertriangle computes the triangle described in the ﬁrst para-

graph of this section. The

mesh object represents a triangle mesh stored as a vertex-

edge-triangle table. The mesh operation

Insert takes as input a triangle, either wholly

or as three indices into the set of vertices managed by the mesh. It returns a reference

to the actual triangle object inserted in the mesh so that the object can be used after

the call. The mesh operation

Remove just removes the speciﬁed triangle. The triangle

object

T is assumed to have an operation T.v(i) that allows you to access the index

of the mesh vertex that the triangle shares. The indices are ordered so that the trian-

gle vertices are counterclockwise ordered. The indexing is modulo 3, so

T.v(0) and

13.8 Delaunay Triangulation 761

T.v(3) are the same integer. The triangle object is also assumed to have an opera-

tion

T.adj(i) that returns a reference to the adjacent triangle that shares the edge

<T.v(i),T.v(i + 1)>. If there is no adjacent triangle to that edge, the reference is null.

The edge object

E is assumed to have an operation E.adj(i) that returns a reference

to an adjacent triangle (at most two such triangles).

Figure 13.46 shows the various quantities used in the pseudocode in the loop

where the stack of triangle pairs is processed. Theoretically, the loop can be inﬁnite if a

triangle pair has all vertices on a common circumcircle. Here is where the typical con-

dition is speciﬁed by the computational geometers: no four points in the input set can

be cocircular. However, an implementation must guard against this when ﬂoating-

point arithmetic is used. It is possible that four points are not exactly cocircular, but

ﬂoating-point round-off errors can make the triangle pair behave as if the points are

cocircular. If such a pair is revisited in the loop, they might very well be swapped back

to their original conﬁguration, and the entire process starts over. To avoid the inﬁ-

nite loop, an implementation can evaluate both circumcircle tests, one for the current

triangle conﬁguration and one for the swapped conﬁguration. If both tests indicate

a swap should occur, then the swap should not be made. Be aware, though, that if

the circumcircle test accepts two adjacent triangles as input, additional care must be

taken to pass the triangles in the same order. Otherwise, the ﬂoating-point calcu-

lations involving the triangles might possibly cause the Boolean return value to dif-

fer. That is, if the function prototype is

bool FirstInCircumcircleOfSecond(Triangle,

Triangle)

, the calls FirstInCircumcircleOfSecond(T0,T1) and FirstInCircumcircle-

OfSecond(T1,T0)

might return different values. One way to obtain a consistent order-

ing is as follows. The two vertices that are opposite the shared edge of the triangles

have indices maintained by the mesh object. Pass the triangles so that the ﬁrst triangle

has the vertex of the smallest index between the two triangles.

Once all the points are inserted into the triangulation and all necessary edge swaps

have occurred, any triangles that exist only because they share a vertex from the su-

pertriangle must be removed. Another potential pitfall here is that all triangles might

be removed. This is the case when the initial points all lie on the same line. If an

application really needs the incremental algorithm to apply to such a set (interpo-

lation based on a collection of data points is one such application), some type of

preprocessing must occur to detect the collinearity. Probably the best bet is to use

the relationship between the 2D Delaunay triangulation and the 3D convex hull that

is described later in this section. The convex hull algorithms appear to be better suited

for handling degeneracies due to the fact that the intrinsic dimensionality of the input

point set is smaller than the dimension of the space in which the points lie.

13.8.2 Incremental Construction in General Dimensions

An attempt at extending the 2D edge swapping algorithm to 3D has a couple of

technical issues to consider. The ﬁrst involves the extension of the linear walk that

was used to ﬁnd a containing triangle. Each input point P is inserted into the current

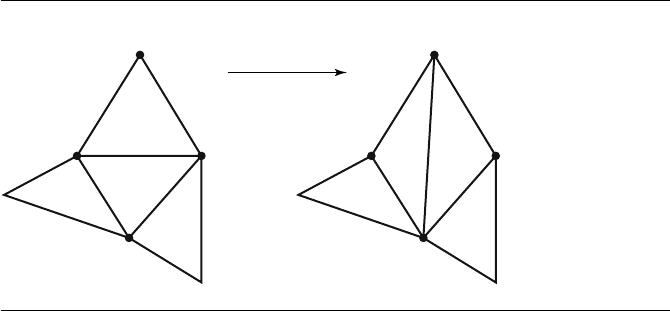
762 Chapter 13 Computational Geometry Topics

v(i

)

v(i

)v(i

)

v(i

)

v(i

)

v(i

)

v(i

)

v(i

)

Edge

swap

Figure 13.46 A triangle pair T , A that needs an edge swap. The index tracking is necessary so

that the correct objects in the vertex-edge-triangle table of the mesh are manipulated.

After the edge swap, up to two new pairs of triangles occur, N

, B

 and N

, B

,

each pair possibly needing an edge swap. These are pushed onto the stack of pairs

that need to be processed.

tetrahedral mesh. A tetrahedron containing P is found using the same type of walk

that was used for the 2D problem. An initial tetrahedron is selected. If P is in that

tetrahedron, the walk is complete. If not, construct a ray whose origin is the average

of the current tetrahedron’s vertices, call it C, and whose direction is P − C.A

tetrahedron face that intersects the ray is located. The tetrahedron adjacent to the

current one and that shares this face is the next candidate for containment of P .

As it turns out, there are pathological data sets for which the walk can be quite

long (Shewchuk 2000). A 3D Delaunay triangulation can have O(n

) tetrahedra.

In the cited paper, it is shown that a line can stab O(n

) tetrahedra. In fact, for d

dimensions, a line can stab on the order of n

d/2

simplices.

The other technical issue is that the swapping mechanism does not have a coun-

terpart in 3D. The edge swapping in 2D was intuitively based on maximizing a mini-

mum angle, but that heuristic does not have a 3D counterpart (Joe 1991). The general

method is based on Watson’s algorithm (Watson 1981). The algorithm is described

for a point set contained in R

whose intrinsic dimensionality is d. That is, the point

set does not lie in a linear space of dimension smaller than d. Unfortunately, an im-

plementation must deal with degeneracy in dimension. A very good description of

the practical problems that occur with implementing Watson’s algorithm in 3D is

presented in Field (1986). This paper is available online through the ACM Digital

Library.

Because of the assumption of full dimensionality of the points, the elements of

the triangulation are nondegenerate simplices, each having d +1 points. The circum-

scribing hypersphere of a simplex will be called a circumhypersphere. The condition

13.8 Delaunay Triangulation 763

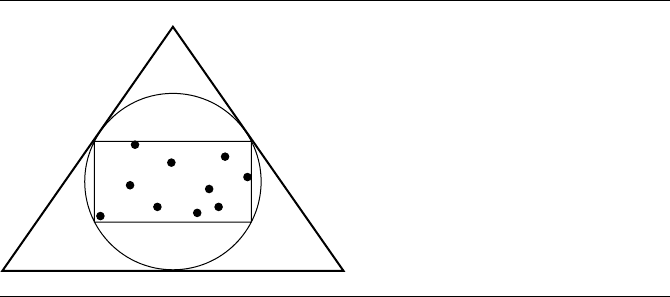
Figure 13.47 Supertriangle of the input point set.

for a Delaunay triangulation is that the circumhypersphere of a simplex does not

contain any input points other than the vertices of that simplex (the empty circum-

hypersphere constraint). The algorithm is described in steps. Following the excellent

presentation in Field (1986), the steps have associated ﬁgures that illustrate what is

happening in two dimensions.

1. Construct a supersimplex, a simplex that is guaranteed to contain the input points

as well as any circumhyperspheres in the ﬁnal triangulation. A suitable choice is a

simplex that contains a hypersphere that itself contains the axis-aligned bounding

box of the input points (see Figure 13.47).

2. The supersimplex is added as the ﬁrst simplex in a mesh of simplices. The

mesh maintains the vertices and all the necessary connectivity between simplices.

Moreover, the circumhypersphere for each simplex is stored to avoid having to

recalculate centers and radii during the incremental updates.

3. Insert the other input points, one at a time, and process as described here.

a. Determine which circumhyperspheres contain the given point. Here is where

the direct appeal is made to satisfying the empty circumhypersphere con-

dition. Before insertion, the empty condition is satisﬁed for all simplices.

When the point is inserted, the simplices corresponding to the circumhyper-

spheres that violate the empty condition must be modiﬁed. The search for

the containing hyperspheres is implemented as a search over simplices us-

ing the (attempted linear) walk described in earlier sections. But as pointed

out in Shewchuk (2000), the worst-case asymptotic order for the stabbing is

O(n

d/2

). Once the containing simplex (or simplices if the input point is on a

shared boundary component) is found, a depth-ﬁrst search can be performed

to ﬁnd other simplices whose circumhyperspheres contain the input point. A