Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

421
Приклад 2. Знайти інтервал збіжності степеневого ряду
...
n
x
...
3
x
2
x
x
2
n
2
3
2
2
+++++
і дослідити його збіжність на
кінцях інтервалу.
Розв
’язування. Оскільки
2
n
n
1
a =
,
,
)1n(
1
а
2
1n
+
=
+
радіус
збіжності
.1
n
1
1lim
n
1n
lim
n
)1n(
lim
)1n(
1
:
n
1
lim
a
a
limR
2
n
2
n
2
2
n
22
n
1n
n
n
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
=
+
==
∞→
∞→∞→∞→
+
∞→
Отже , даний ряд абсолютно збігається в інтервалі ).1,1(−
Дослідимо степеневий ряд на кінцях інтервалу, тобто в точках
.1x,1x =−=
При
1x =
отримуємо числовий ряд
...
n
1
...
3
1
2
1
1
222
+++++
.
Для дослідження збіжності ряду використаємо інтегральну
ознаку Коші. Для цього обчислимо інтеграл
.1)1
N
1
(lim
1
N
x
1
lim
1
N
)
x
1
(lim
x
dx
lim
x
dx
NNN
N
1
2
N
1
2
=−−=−=−==
→∞→∞→∞→∞
∞
∫∫
Невласний інтеграл збігається , значить, і числовий ряд теж
збігається, тобто правий кінець входить в інтервал збіжності.
При
1x −=
одержимо числовий ряд
...,
n
)1(
...
3
1
2
1
1
2
n
22
+
−
++−+−
який збігається абсолютно, тому що
виконуються умови ознаки Лейбніца:
...
3
1
2
1
1
22
>>> ;
0
n
1
lim
2
n
=
∞→
і збігається ряд , складений з абсолютних величин. Та-
ким чином, вихідний степеневий ряд абсолютно збігається на відріз-
ку
[]
.1,1−
422
Приклад 3. Знайти інтервал збіжності степеневого ряду
...
10
x!n
...x
10
!2
x
10
!1
1
n
n
2
2
+++++
.
Розв
’язування. Оскільки
n
n
10
!n
a =
,
1n
1n
10
)!1n(
a
+
+
+
=
,
то
.0
1n
10
lim
)!1n(10
!n10
lim
10
)!1n(
:
10
!n
limR
n
n
1n
n
1nn
n
=
+
=
+
=
+
=
→∞
+
→∞
+
→∞
Це означає, що ряд збігається тільки при
0x = і розбігається
при інших значеннях.
Приклад
4. Знайти інтервал збіжності степеневого ряду
...)3x(
n
1
...)3x(
3
1
)3x(
2
1
)3x(
n
2
3
2
2
2
+−++−+−+− .
Розв
’язування. Тут
2
n
n
1
a =
,
2
1n
)1n(
1
a
+
=
+
,
.1)
n
1
1(lim
n
)1n(
lim
)1n(
1
:
n
1
limR
2
n
2
2
n
22
n
=+=
+
=
+
=
→∞→∞→∞
Значить, ряд збігається, якщо
13x1 <−<− , тобто інтервал
збіжності степеневого ряду
4x2 << .
Дослідимо збіжність степеневого ряду на кінцях інтервалу
збіжності. При
4x = одержимо ряд
...
n
1
...
3
1
2
1
1
222
+++++
.
Даний ряд збігається, оскільки, згідно з інтегральною ознакою
Коші, невласний інтеграл
1)1
N
1
(lim
1
N
)
x
1
(limdxxlim
x
dx
NN
N
1
2
1
N
2
=−−=−==
→∞→∞
−
∞
→∞
∫∫
є збіжним.
Якщо
2x = , то одержимо знакозмінний ряд
...
n
1
)1(...
3
1
2
1
1
222
+−++−+− .
Цей ряд збігається, оскільки виконуються умови ознаки
Лейбніца:
1)
...
3
1
2
1
1
22
>>>
, 2)
0
n
1
lim
2
n
=
∞→

423
Крім цього, знакозмінний ряд збігається абсолютно, тому що
збігається ряд з абсолютних величин його членів.
Приклад
5. Дослідити збіжність ряду
...)10x(!n...)10x(!3)10x(!2)10x(!1
n32
+−++−+−+− .
Розв
’язування. Оскільки
,!na
n
=
)!1n(a
1n
+=
+
, то
.0
1n
1
lim
)1n(!n
!n
lim
)!1n(
!n
limR
nnn
=
+
=
+
=
+
=
∞→∞→∞→
Це означає, що ряд збігається тільки при
,010x =− тобто в
точці
.10x =
§8. Диференціювання та інтегрування степеневих рядів.
Розклад деяких функцій в степеневі ряди
Приведемо дві важливі теореми (без доведення).
ТЕОРЕМА 1. Степеневий ряд
...xa...xaxaa
n
n
2
210
+++++
(8.33)
і
одержаний із нього почленним диференціюванням ряд
...xna...xa4xa3xa2a
1n
n
3
4
2
321
++++++
−
(8.34)
мають один і той же інтервал збіжності
).R,R(−
Сума ряду (8.34)
дорівнює похідній
)x(S
′
суми )x(S ряду (8.33) при всіх значен-
нях
x
, для яких R|x| < .
ТЕОРЕМА
2. Степеневий ряд
...xa...xaxaa
n
n
2
210
+++++ (8.35)
і ряд ...x
n
a
...x
3
a
x
2
a
xa
n
1n
3
2
2
1
0
+++++
−
(8.36)
одержаний із ряду (8.35) почленним інтегруванням, мають од-
наковий інтервал збіжності. Сума ряду (8.36) дорівнює
∫
=
x
0
,dx)x(S)x(F де
)x(S
- сума ряду (8.35).
Для практики важливо вміти дану функцію )x(f розкласти в
степеневий ряд, тобто функцію
)x(f
представити у вигляді степе-
невого ряду, що дає можливість досить просто обчислювати значен-
ня цієї функції.
424
Спочатку розглянемо деякі часткові випадки. Розглянемо сте-
пеневий ряд
...x...xx1
n2
+++++ . (8.37)
Цей ряд являє собою ряд геометричної прогресії із знаменни-
ком
x
, який збіжний при
1x <
і його сума рівна
x1
1
−
.
Отже, ми можемо записати:
...x...xx1
x1
1
n2
+++++=
−
(8.38)
На останню рівність можна дивитися як на розклад функції
x1
1
−
в степеневий ряд. Із розкладу (8.38) можна легко одержати
інші розклади функцій.
Розклад
функції
)x1ln()x(f +=
.
Замінивши в розкладі (8.38)
x
на )у(− , будемо мати:
...y)1...(yy1
y1
1
nn2
+−++−=
+
. (8.39)
Якщо
1xy0 <≤≤ , то рівність (8.39), як було сказано в поперед-
ньому параграфі, можна проінтегрувати почленно по
у
в межах від
0 до
x
, тобто
∫∫ ∫∫
+−++−=
+
x
0
x
0
x
0
nn
x
0
...dyy)1(...yddy
y1
dy
Звідси маємо:
...
1n
x
)1...(
3
x
2
x
x)x1ln(
1n
n
32
+
+
−−+−=+
+
, x <1.
Такий розклад справедливий також для
1x = і відповідно ряд
...
3
1
2
1
12ln −+−=
є збіжним. Область збіжності буде множи-
на
∈
x
(
]
1,1−
.
Розклад
функції
arctgx)x(f =
Покладемо в розкладі (8.38) .yx
2
−=
...y)1(...yy1
y1
1
n2n42
2
+−+−+−=
+
(8.40)
425
Помноживши останню рівність на
dy
і проінтегрувавши поч-
ленно в межах від 0 до
x
, де ,1x < одержимо:
∫∫∫ ∫∫
+−+−+−=
+
x
0
x
0
x
0
x
0
n2n
x
0
42
2
...dyy)1(...dyydyydy
y1
dy
або
...
0
x
1n2
y
)1(...
0
x
5
y
0
x
3
y
0
x
y
0
x
arctgy
1n2
n
53
+
+
−+−+−=
+
.
Оскільки
,00arctg = то маємо:
...
1n2
x
)1(...
5
x
3
x
xarctgx
1n2
n
53
+
+
−+−+−=
+
, якщо x <1. (8.41)
Можна довести, що цей розклад є справедливим при
1x −= і
.1x =
При
1x = маємо: ...
7
1
5
1
3
1
1
4
1arctg +−+−=
π
=
.
При
1x −= маємо: ...
7
1
5
1
3
1
1
4
)1(arctg −+−+−=
π
−=−
.
Отже, область збіжності даного степеневого ряду буде відрі-
зок
[]
1;1− .
Ми бачимо, що деякі функції, як, наприклад
)x1ln( + ,
arctgx
і тому подібні, допускають розклад в степеневий ряд відносно аргу-
менту
x
. Природно поставити загальне питання про розклад даної
функції
)x(f по зростаючим цілим додатнім степеням
x
. Цим пи-
танням ми займемось в наступному параграфі.
§ 9. Розклад функції в ряд Маклорена
Припустимо, що дана функція
)x(f може бути розкладена в
степеневий ряд
...xa...xaxaa)x(f
n
n
2
210
+++++=
, (8.42)
де
,...n10
a,...,a,a
- невизначені коефіцієнти, причому інтервал збіж-
ності
()
R,R−
не зводиться до точки, тобто 0R > .
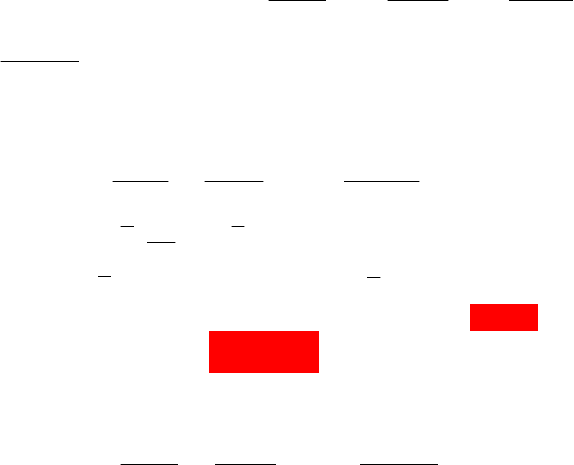
Як було сказано вище, степеневий ряд (8.42) в його інтервалі
збіжності можна диференціювати почленно будь-яке число раз,
причому всі одержані ряди будуть збігатися і їх суми будуть дорів-
нювати відповідним похідним від суми даного ряду
).x(f
426
Продиференціювавши почленно ряд (8.42)
n
раз , будемо ма-
ти:
...xna...xa3xa2a)x(f
1n
n
2
321
+++++=
′
−
,
...xna)1n(...xa43xa32a2)x(f
2n
n
2
432
+−++⋅+⋅+=
′′
−
...xna)1n)(2n(...xa543xa432a32)x(f
3n
n
2
543
+−−++⋅⋅+⋅⋅+⋅=
′′′
−
...x
1
n
a)1n(n...21
n
a...321)x(
)n(
f +
+
+⋅⋅+⋅⋅=
.
Поклавши в цих рівностях, включаючи (8.42), х
=0 одержимо:
;a)0(f
0
= ;a)0(f
1
=
′
;a2)0(f
2
=
′′
3
a32)0(f ⋅=
′′′
;
.an...321)0(f
n
)n(
⋅⋅⋅=
Звідси
);0(fa
0
= ;
!1
)0(f
a
1
′
=
;
!2
)0(f
a
2
′′
=
;...
!3
)0(f
a
3
′′′
=
!n
)0(f
a
)n(
n
= .
Підставивши значення коефіцієнтів
n10
a,...,a,a
в (8.42), оде-
ржимо формулу Маклорена:
)x(Rx
!n
)0(f
...x
!2
)0(f
x
!1
)0(f
)0(f)x(f
n
n
)n(
2
+++
′′
+
′
+=
, (8.43)
де
!
n
x
)x(f)x(R
n
)n(
n
= (
xx0 <<
) – залишковий член у формі Ла-
гранжа. Число
x можна записати у вигляді xx θ= , .10 <θ<
Якщо при необмеженому зростанні n, тобто при ∞→
n
,0Rlim
n
n
=
∞→
(8.44)
то із формули Маклорена одержимо розклад функції
)x(f
в ряд по
степенях
x
, який називається рядом Маклорена:
...x
!n
)0(f
...x
!2
)0(f
x
!1
)0(f
)0(f)x(f
n
)n(
2
+++
′′
+
′
+= (8.45)
А умова (8.44) являє собою необхідну і достатню умову того,
що ряд Маклорена для функції
)x(f , яка диференційована необ-
межене число разів, збігається до цієї функції.
Приведемо приклади на застосування ряду Маклорена до роз-
кладу деяких елементарних функцій в степеневі ряди.
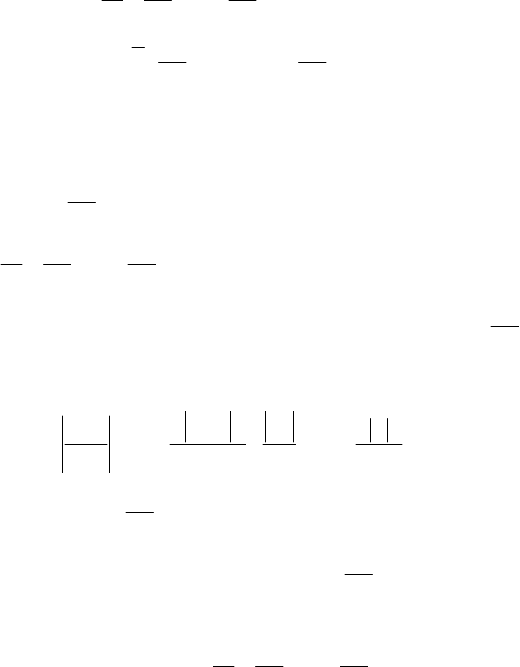
427
Розклад функції .e)x(f
x
=
Нехай
.e)x(f
x
=
Тоді
,e)x(f
x
=
′
,e)x(f
x
=
′′
…
.e)x(f
x)n(
=
Поклавши
0x = , одержимо:
;1e)0(f
0
== ;1)0(f =
′
;1)0(f =
′′
… .1)0(f
)n(
=
Підставивши ці значення в формулу Маклорена (8.43) , буде-
мо мати:
)x(R
!n
x
...
!2
x
!1
x
1e
n
n2
x
+++++= ,
де
!n
x
)x(f
!n
x
)x(f)x(R
n
)n(
n
)n(
n
θ== .
Оскільки
x)n(
e)x(f
θ
=θ - величина обмежена при обмежено-
му
,
x
то, для того, щоб довести, що 0Rlim
n
n
=
∞→
, потрібно показа-
ти,що
0
!n
x
lim
n
n
=
∞→
. Для того зафіксуємо
x
і розглянемо ряд
....
!n
x
...
!2
x
!1
x
1
n2
+++++
Якщо він збігається, то його загальний член
!n
x
u
n
n
= при
∞→
n
прямує до нуля. Використаємо ознаку Даламбера до ряду
абсолютних величин:
.10
1n
x
lim
!n
x
:
)!1n(
x
lim
u
u
lim
n
n1n
n
n
1n
n
<=
+
=
+
=
∞→
+
∞→
+
∞→
Отже,
0
!n
x
lim
n
n
=
∞→
.
Таким чином
0
!n
x
elim)x(Rlim
n
x
n
n
n
==
θ
∞→∞→
і функція
x
e)x(f =
розкладається в інтервалі
),( ∞−∞
в слідуючий ряд Маклорена
...
!n
x
...
!2
x
!1
x
1e
n2
x
+++++= (8.46)
Розклад
функцій xsin)x(f = , соsx)x(f =
Нехай xsin)x(f = ; звідси

428
xcos)x(f =
′
, xsin)x(f −=
′′
, xcos)x(f −=
′′′
, xsin)x(f
ІV
= ,…
Поклавши х
=0, маємо :
;0)0(f = ;1)0(f =
′
;0)0(f =
′′
;1)0(f −=
′′′
;0)0(f
v1
= …
Підставивши ці значення у формулу (8.45), одержимо:
...
)!1n2(
x
)1(...
!5
x
!3
x
!1
x
xsin
1n2
1n
53
+
−
−+−+−=
−
−
. (8.47)
Можна легко переконатися, що ряд збігається для будь-
якого
).,(x ∞−∞∈
Зробивши аналогічні викладки, можна знайти розклад функ-
ції
соsx)x(f =
в ряд:
...
)!n2(
x)1(
...
!6
x
!4
x
!2
x
1xcos
n2n642
+
−
+−+−= для
),(x ∞−∞∈
(8.48).
Розклад
бінома Ньютона
m
)x1()x(f +=
Нехай
m
)x1()x(f +=
, де −
m
число ціле або дробове, дода-
тне або від’ємне.
Тоді маємо:
,)x1(m)x(f
1m−
+=
′
,)x1)(1m(m)x(f
2m−
+−=
′′
,)x1)(2m)(1m(m)x(f
3m−
+−−=
′′′
…….…………………………………………
,)x1)(1nm)...(2m)(1m(m)x(f
nm)n( −
++−−−=
………….……………………………………………………
Поклавши
0x =
у всіх цих формулах, одержимо:
;1)0(f =
;m)0(f =
′
);1m(m)0(f −=
′′
)2m)(1m(m)0(f −−=
′′′
),..1nm)...(2m)(1m(m)0(f
)n(
+−−−=
.
Підставивши вирази для
)0(f),...0(f),0(f
)n(
′
в ряд Маклорена
(8.45) будемо мати
...x
!n
)1nm)...(2m)(1m(m
...x
!3
)2m)(1m(m
x
!2
)1m(m
x
!1
m
1)x1(
n
32m
+
+−−−
+
+
−−
+
−
++=+
(8.49)
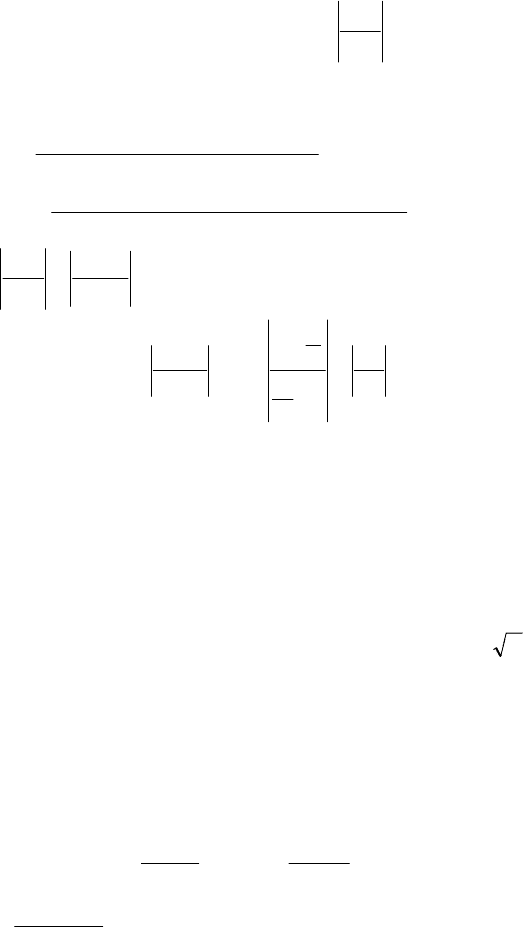
429
Користуючись формулою
1n
n
n
a
a
limR
+
→∞
= , знайдемо інтервал
збіжності
()
R,R− ряду (8.49).
Ми маємо:
,
n...321
)1nm)...(2m)(1m(m
a
n
⋅⋅⋅⋅
+−−−
=
.
)1n(n...21
)nm)(1nm)...(2m)(1m(m
a
1n
+⋅⋅⋅
−+−−−
=
+
Звідси
nm
1n
a
a
1n
n
−
+
=
+
, і відповідно
.1
1
1
1
n
m
n
1
1
lim
nm
1n
limR
nn
=
−
=
−
+
=
−
+
=
∞→∞→
(8.50)
Таким чином, біноміальний ряд збігається для
()
1,1x −∈ і
розбігається зовні. Чи збігається цей ряд в точках
1x −= і 1x = ,
необхідно досліджувати для кожного випадку окремо.
§10. Розклад функції в ряд Тейлора
В деяких випадках функція
)x(f або її похідні втрачають
зміст в точці
0x = , як, наприклад
xln)x(f =
або
x)x(f =
.
Такі функції не можуть бути розкладені в ряд Маклорена. Для
розкладу такого роду функцій можна скористатись більш загальни-
ми степеневими рядами, розкладеними за степенями
),ax( −
де
−
a
підібране, в конкретному випадку, постійне число.
В розділі 4 було доведено, що якщо функція
)x(f диферен-
ційована
n
раз в інтервалі
)x,a(
,то має місце формула Тейлора:
,R)ax(
)!1n(
)a(f
...)ax(
!2
)a(f
)ax(
!1
)a(f
)a(f)x(f
n
1n
)1n(
2
+−
−
+
+−
′′
+−
′
+=
−
−
(8.51)

430
де
!n
)ax(
)c(fR
n
)n(
n
−
=
(
x
c
a
<< ) – залишковий член у формі Ла-
гранжа. Число с можна записати у вигляді )ax(aс −θ+= , де
10 <θ< .
Якщо при необмеженому зростанні
n
, тобто при ∞→
n
,
,0Rlim
n
n
=
∞→
(8.52)
то із формули Тейлора одержимо розклад функції
)x(f в ряд по
степенях
)ax( − , який називається рядом Тейлора:
...)ax(
!
n
)a(f
...)ax(
!2
)a(f
)ax(
!1
)a(f
)a(f)x(f
n
)n(
2
+−+
+−
′′
+−
′
+=
(8.53)
Умова (8.52) служить необхідною і достатньою умовою того, що
ряд Тейлора для функції, яка необмежене число раз диференційова-
на, збігається до цієї функції.
Приклад
. Розкласти в ряд за степенями )ax( − функцію
a
x
e)x(f =
.
Розв
’язування. Продиференціюємо функцію
)x(f
:
,...e
a
1
)x(f,...,e
а
1
)x(f,e
а
1
)x(f,e
a
1
)x(f
a
x
n
)n(
a
x
3
a
x
2
a
x
==
′′′
=
′′
=
′
Підставивши
a
x
= в попередні формули, одержимо:
,...
a
e
)a(f,...
a
e
)a(f
,a
e
)a(f,
a
e
)a(f,e)a(f
n
)n(
32
==
′′′
=
′′
=
′
= Ви-
користовуючи ряд Тейлора (8.53), одержимо такий розклад функції
)x(f по степенях )ax( − :
...)ax(
a
!
n
e
...)ax(
a!3
e
)ax(
a!2
e
)ax(
!1
e
e)x(f
n
n
3
3
2
2
+−+
++−+−+−+=
Знаходимо радіус збіжності даного ряду:
1n
n
n
a
a
limR
+
∞→
=
. Тут
