Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

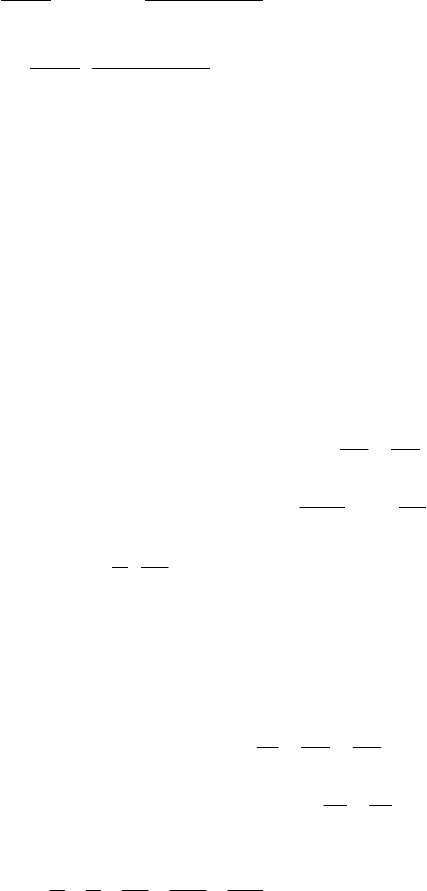
431
1n
1n
n
n
a)!1n(
e
a,
a!n
e
a
+
+
+
==
.
,a)1n(lim
e
a)!1n(
a!n
e
limR
n
1n
n
n
∞=⋅+=
+
⋅=
∞→
+
∞→
при будь-якому
.0a ≠
Отже, область збіжності ряду буде
),( ∞−∞
§11.
Застосування степеневих рядів до
наближених обчислень
Одержані розклади деяких функцій в степеневі ряди в §10,11
дають можливість наближено обчислювати значення функції, ви-
значені інтеграли, границі функції і т.д.
Приклад
1. Обчислити
5cos , обмежившись двома членами
розкладу.
Розв
’язування. Використаємо формулу розкладу
х
cos
в ряд за
зростаючими степенями
x
: ...
!4
x
!2
x
1хcos
42
−+−= .
Переведемо
5 в радіанну міру: .
36
5
180
5
π
=⋅
π
=
Тоді
2
)
36
(
2
1
15cos
π
−≈
. Підставивши замість ,14159,3≈π одер-
жимо
.9962,05cos ≈
Приклад
2. Обчислити число
e
.
Розв
’язування. Використаємо розклад функції
x
e
в ряд Мак-
лорена:
...
!3
x
!2
x
!1
x
1e
32
x
++++=
.
Поклавши
1x =
, одержимо
...
!
3
1
!
2
1
11e ++++=
. Якщо за набли-
жене значення числа
e
взяти суму перших семи членів цього ряду
,
720
1
120
1
24
1
6
1
2
1
11e ++++++≈
то одержимо .718,2e ≈

432
Приклад 3. Обчислити
5
1,1 з точністю до 0,001.
Розв
’язування. Використаємо формулу біноміального ряду
...x
!
2
)1m(m
!
1
mx
1)x1(
2m
+
−
++=+
.
Якщо
1,0x =
, ,
5
1
m =
то одержимо
.019,1
0008,002,01...01,0
!2
)1
5
1
(
5
1
1,0
5
1
1)1,01(1,1
5
1
5
≈
≈−+=+
−
+⋅+=+=
Оскільки в знакопереміжному ряді із спадними по абсолютній вели-
чині членами
,uR
1nn +
<
то похибка в наших обчисленнях не пере-
вищує
0,0008, що забезпечує необхідну точність.
Приклад
4. Обчислити ,130
3
обмежившись двома членами
розкладу.
Розв
'язування. Запишемо число
3
130 у вигляді
.)
25
1
1(55125130
3
1
33
+=+=
У нашому випадку , поклавши в біноміальному ряді
,
25
1
x
=
,
3
1
m =
матимемо
.
15
1
5)
25
1
3
1
1(5130
3
=⋅+≈
Приклад
5. Обчислити 10ln , обмежившись трьома членами
розкладу.
Розв
'язування. Число 10ln представимо так:,
.
)4
1
1ln(2ln3)
4
1
1(2ln)22ln(10ln
33
++=+=+= Поклавши у фор-
мулі
...
3
x
2
x
x)x1ln(
32
−+−=+
значення
4
1
x,1x
==
, одержимо
,693,0...
3
1
2
1
12ln ≈−+−=
.219,0...
43
1
42
1
4
1
)
4
1
1ln(
32
≈−
⋅
+
⋅
−=+
Тоді
.298,2219,0019,210ln =+=
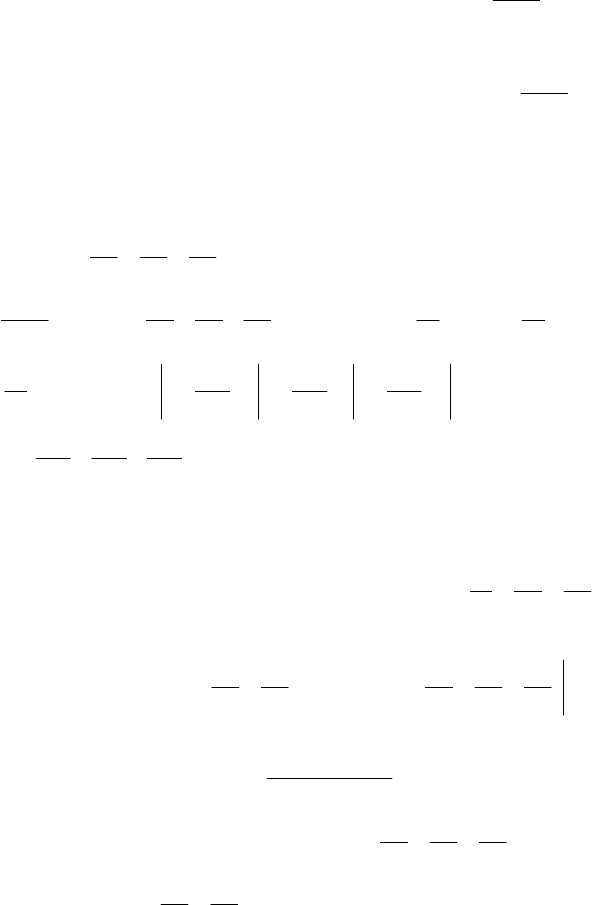
433
Приклад 6. Обчислити визначений інтеграл ,dx
x
xsin
1
0
∫
обме-
жившись чотирма членами розкладу функції
.xsin
Розв
’язування. Оскільки невизначений інтеграл ,dx
x
xsin
∫
не
може бути виражений в елементарних функціях і формулу Ньюто-
на-Лейбніца не можна використати, даний інтеграл обчислимо на-
ближено, використовуючи теорію рядів. Розділимо праву частину
розкладу функції
xsin
в ряд
...
!
7
x
!
5
x
!
3
x
xxsin
753
+−+−=
на х і проінтегруємо одержаний вираз:
.9461,0...
7
!
7
1
5
!
5
1
3
!
3
1
1
...
0
1
x
7!7
1
0
1
x
5!5
1
0
1
x
3!3
1
0
1
x...dxx
!7
1
dxx
!5
1
dxx
!3
1
dxdx...)
!7
x
!5
x
!3
x
1(dx
x
xsin
753
1
0
6
1
0
1
0
4
1
0
2
64
1
0
2
1
0
≈+−+−=
=+−+−=+−
−+−=+−+−=
∫
∫∫∫∫∫
Приклад
7. Обчислити .dxe
3,0
0
x
2
∫
−
Розв
’язування. Замінивши в рівності
...
!
3
x
!
2
x
!
1
x
1e
32
x
++++=
x
на ”-
2
x ” і проінтегрувавши в межах від 0 до 0,3, одержимо
.291,0
0
3,0
42
x
10
x
3
x
xdx...)
6
x
2
x
x1(dxe
75364
2
3,0
0
3,0
0
x
2
≈
⎥
⎦
⎤
⎢
⎣
⎡
−+−=+−+−=
∫∫
−
Приклад
8. Знайти
.
x
arctgxxsin
lim
3
0x
−
→
Розв
’язування. Оскільки
...
!
7
x
!
5
x
!
3
x
xxsin
753
+−+−=
,
...,
5
x
3
x
xarctgx
53
−+−= то

434
.
6
1
...x)
!5
1
5
1
()
!3
1
3
1
(lim
x
...
5
x
3
x
x...
!5
x
!3
x
x
lim
x
arctgxxsin
lim
2
0x
3
5353
0x
3
0x
=
⎥
⎦
⎤
⎢
⎣
⎡
+−−−=
=
+−+−−+−
=
−
→
→→
Приклад
9. Знайти розв’язок диференціального рівняння
,xcosxyyxy =+
′
+
′′
(8.54)
який задовольняє початковим умовам
;0)0(y =
1)0(y =
′
. (8.55)
Розв
’язування. Шукаємо розв’язок
y
у вигляді ряду
....xa...xaxaay
n
n
2
210
+++++=
(8.56)
Знайшовши похідну
y
′
і використавши (8.55), одержимо
;0a
0
= .1a
1
=
Тоді
...xaxaxy
n
n
2
2
++++=
Продиференціювавши розклад
y
два рази, одержимо:
...xa34xa23a2y
...xa4xa3xa21y
2
432
3
4
2
32
+⋅+⋅+=
′′
++++=
′
Підставивши
y,y,y
′′′
в (8.54) і замінивши
x
cos
його розк-
ладом (8.48), знаходимо:
...).
!
4
x
!
2
x
1(x...xaxax
...)xa3xa21(x...xa43xa32a2
42
3
3
2
2
2
32
2
432
−+−=++++
++++++⋅+⋅+
Прирівнявши коефіцієнти при однакових степенях
x
, одер-
жимо:
!4
1
aa5a76
0aa4a65
!2
1
aa3a54
0aa2a43
12a32
0a2
557
446
335
224
3
2
=++⋅
=++⋅
−=++⋅
=++⋅
=+⋅
=
х
2
х
х
3
х
4
х
5
1

435
Звідси випливає, що ;0...aaaa
8642
=====
,...
!9
1
a,
!7
1
a6
!4
1
76
1
a
,
!5
1
a4
!2
1
54
1
a,
!3
1
a
957
353
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−−
⋅
=−=
(8.57)
Підставивши постійні (8.57) в розклад (8.56) маємо:
...
!
7
x
!
5
x
!
3
x
xy
753
+−+−= , що відповідає розкладу функції xsiny =
по степенях
.
x
Перевірка. Підставимо
xsiny,xcosy,xsiny −=
′′
=
′
= у
рівняння (8.54):
.xcosxxcosx,xcosxxsinxcosxxsin ==++−
Розв’язок рівняння (8.54) знайдено правильно.
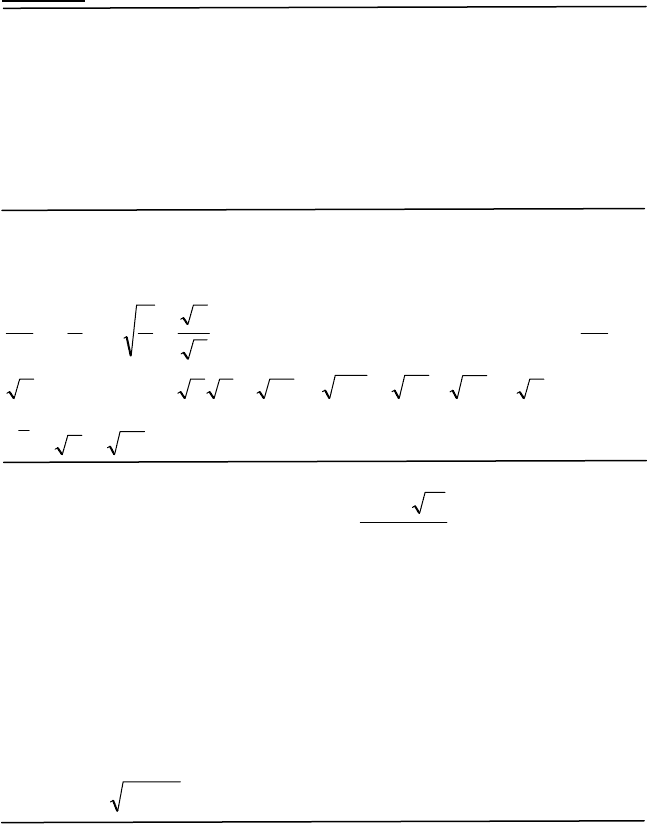
436
ДЕЯКІ ОЗНАЧЕННЯ І ФОРМУЛИ ЕЛЕМЕНТАРНОЇ
МАТЕМАТИКИ
Алгебра
Формули скороченого множення і розклад на множники
()
22
2
bab2aba +±=±
,
()
3223
3
bab3ba3aba ±+±=±
;
()()
bababa
22
−+=− ,
()
()
2233
babababa +±=± ∓ ,
()
()
1n3n22n1nnn
a...xaaxxaxax
−−−−
++++−=− .
Для квадратного тричлена
()()
21
2
xxxxacbxax −−=++ , де
1
x і
2
x - корені рівняння: 0cbxax
2
=++ .
Степені
й корені
n
n
a...aaa ⋅⋅⋅=
.
qpqp
aaa
+
=⋅ ,
p
a :
qpq
aa
−
= ,
()
pq
q
p
aa =
,
p
p
p
b
a
b
a
⎟
⎠
⎞
⎜
⎝
⎛
= ,
p
p
p
b
a
b
a
= ,
()
p
pp
abba =⋅ , 1a
0
= , aa
1
= ,
p
p
a
1
a =
−
,
abba
n
n
==>= ,
ppp
abba = ,
p
q
pk
qk
aa =
,
()
q
p
p
q
aa =
,
p
p
1
aa =
,
p/q
p
q
aa = .
Квадратне
рівняння
0cbxax
2
=++ ;
()
0a ≠ ;
a
2
Db
x
2,1
±−
=
, ac4bD
2
−= .
21
xx0D ≠→> ;
21
xx0D =→=
→< 0D
немає коренів в
R
.
Теорема Вієта: якщо
1
x
і
2
x
- корені рівняння
0cbxax
2
=++ , то
a/bxx
21
−=+
;
a/cxx
21
=⋅
.
Зведене квадратне рівняння:
а=1, 0qpxx
2
=++ , якщо
1
x і
2
x - корені, то pxx
21
−=+ ,
qxx
21
=⋅ .
Якщо
k2p = (
p
- парне число) і 0qkx2x
2
=++ , то
qkkx
2
2,1
−±−= .
Логарифми
xabxlog
b
a
==>=
; 0a > 1a ≠ ; xa
xlog
a
= ;
1alog
a
=
;
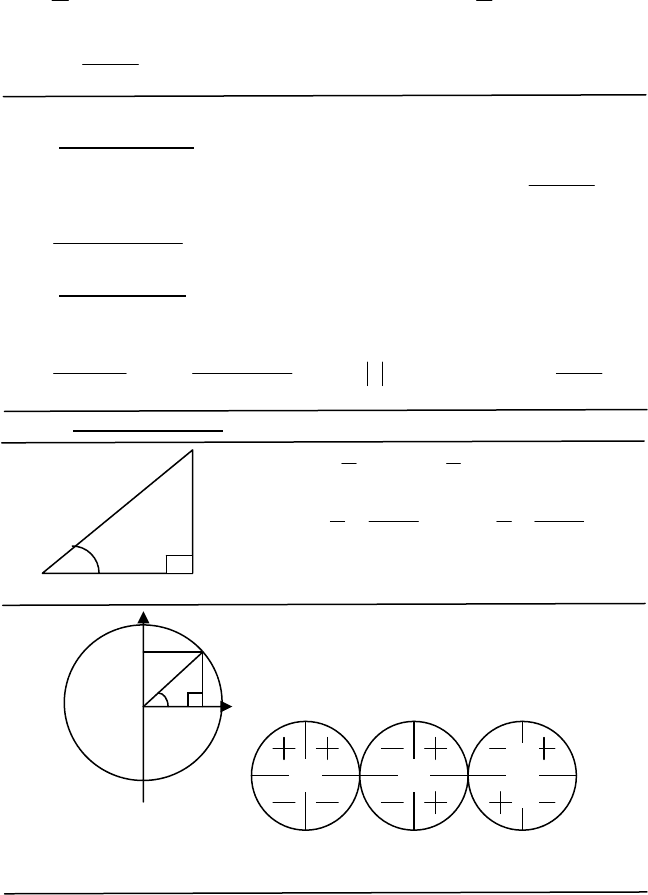
437
01log
a
= , ylogxlogxylog
aaa
+= , xlogkxlog
a
k
a
=
ylogxlog
y
x
log
aaa
−= ,
()
0x >
()
0y >
; xlog
k
1
xlog
a
a
k
= ;
()
0x >
alog
xlog
xlog
c
c
a
=
;
()
1c,0c ≠> xlgxlog
10
= ; xlnxlog
e
=
Прогресії
Арифметична
{}
÷
n
a
daa
1nn
+=
−
,
1n1nn
aaa2
+−
+= ,
()
1ndaa
1n
−+= , n
2
aa
S
n1
n
⋅
+
= ,
()
n
2
1nda2
S
1
n
⋅
−+
=
n21n
a...aaS +++=
Геометрична
{}
n
b÷÷
qbb
1nn
⋅=
−
,
1n1n
2
n
bbb
+−
⋅= ,
1n
1n
qbb
−
⋅= ,
1q
bqb
S
1n
n
−
−
=
,
()
1q
1qb
S
n
1
n
−
−⋅
=
, якщо
1q <
,
∞→
n
,
q1
b
S
1
n
−
=
.
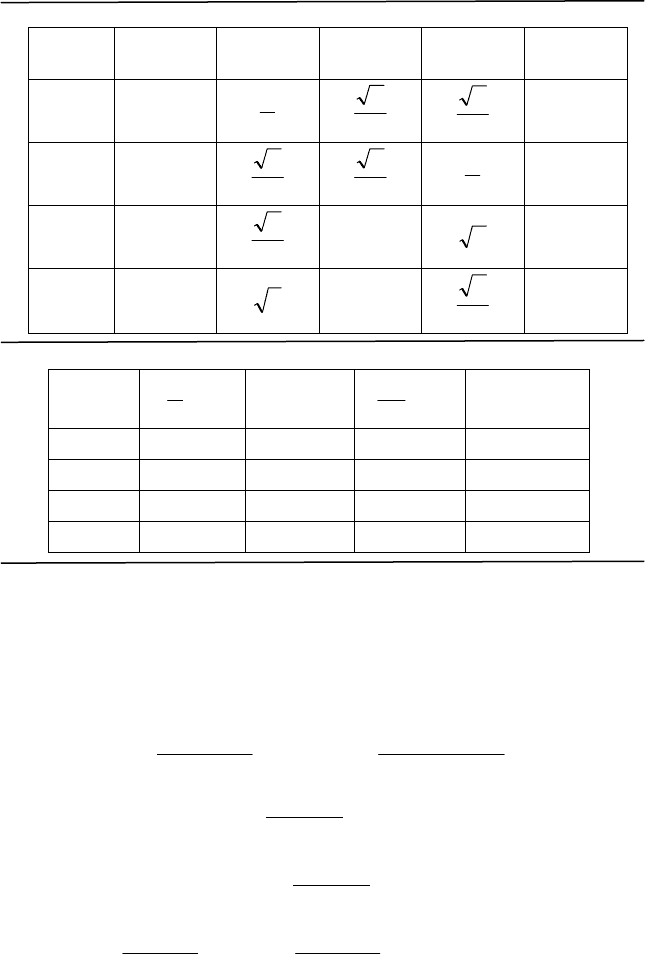
Тригонометрія
c
a
sin =α
;
c
b
cos =α
;
α
α
==α
cos
sin
b
a
tg
;
α
α
==α
sin
cos
a
b
ctg ;
ysin =α
,
x
cos
=α
a c
b
α
P
(x;
y)
y
x
R=1
α
sin
cos
tg
ctg
438
Значення тригонометричних функцій
0
°
0
30
°
π/6
45
°
π/4
60
°
π/3
90
°
π/2
sin
0
2
1
2
2
2
3
1
cos
1
2
3
2
2
2
1
0
tg
0
3
3
1
3
не існує
с
tg
не існує
3
1
3
3
0
Формули зведення
β
α±
π
2
απ ∓ α
π
∓
2
3
α−π2
β
sin
α
cos
α± sin
α−
cos
α− sin
β
cos
αsin∓
π−
cos
αsin∓
α
cos
β
tg αctg∓ αtg∓
α±
ctg
α−
tg
β
ctg αtg∓ αctg∓
α±
tg
α−
ctg
Формули перетворення
1cossin
22
=α+α
; 1ctgtg =α⋅α ;
α=α+
22
sectg1 ; α=α+
22
seccosctg1 ;
()
β
α±
β
α=
β
±α sincoscossinsin
;
()
β
α
β
α=
β
±α sinsincoscoscos ∓
;
()
βα
β
±α
=β±α
tgtg1
tgtg
tg
∓
;
()
β±α
β
⋅α
=β±α
ctgctg
1ctgctg
ctg
∓
;
α+
α
=αα=α
2
tg1
tg2
cossin22sin
;
α+
α−
=α−α=α
2
2
22
tg1
tg1
sincos2cos
;
α−
α
=α
2
tg1
tg2
2tg
;
α
−α
=α
ctg2
1ctg
2ctg
2
;
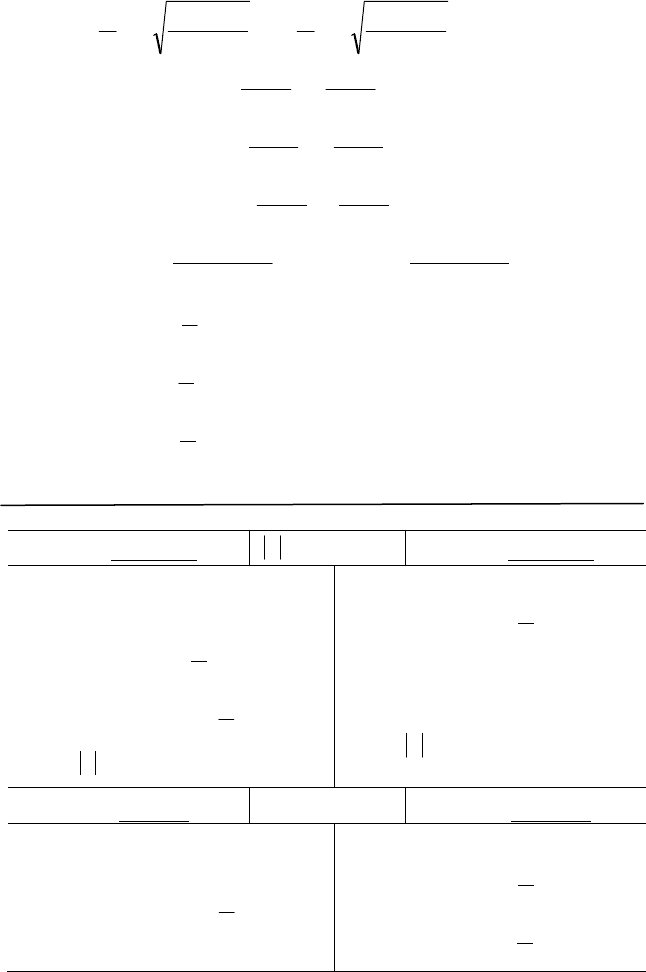
439
2
cos1
2
sin
α−
±=
α
;
2
cos1
2
cos
α+
±=
α
;
2
cos
2
sin2sinsin
β
α
β
±α
=β±α
∓
;
2
cos
2
cos2coscos
β
−α
β
+α
=β+α
;
2
sin
2
sin2coscos
β
−α
β
+α
−=β−α
;
βα
β
±α
=β±α
coscos
)sin(
tgtg
;
βα
α±
β
=β±α
sinsin
)sin(
ctgctg
;
()()
[]
β−α+β+α=βα coscos
2
1
coscos
;
()()
[]
β+α−β−α=βα coscos
2
1
sinsin ;
()()
[]
β−α+β+α=βα sinsin
2
1
cossin ;
α−α=α
3
sin4sin33sin ; α−α=α cos3cos43cos
3
;
Тригонометричні рівняння
axsin = ;
1a ≤ ; zk ∈
a
x
cos
= ;
()
π+×−= kaarcsin1x
k
;
π=→= kx0a ;
π+
π
=→= k
2
x1a
;
π+
π
−=→−= k
2
x1a ;
∅∈→> x1a
π+±= k2aarccosx ;
π+
π
=→= k
2
x0a ;
π=→= k2x1a ;
π+π=→−= k2x1a ;
∅∈→> x1a
a
tgx
= ; Rm∈ ; zk ∈
a
ctgx
= ;
π+= karctgax ;
π=→= kx0a
;
π+
π
±=→±= k
4
x1a
;
π+= karctgax ;
π+
π
=→= k
2
x0a
;
π+
π
=→= k
4
x1a ;
440
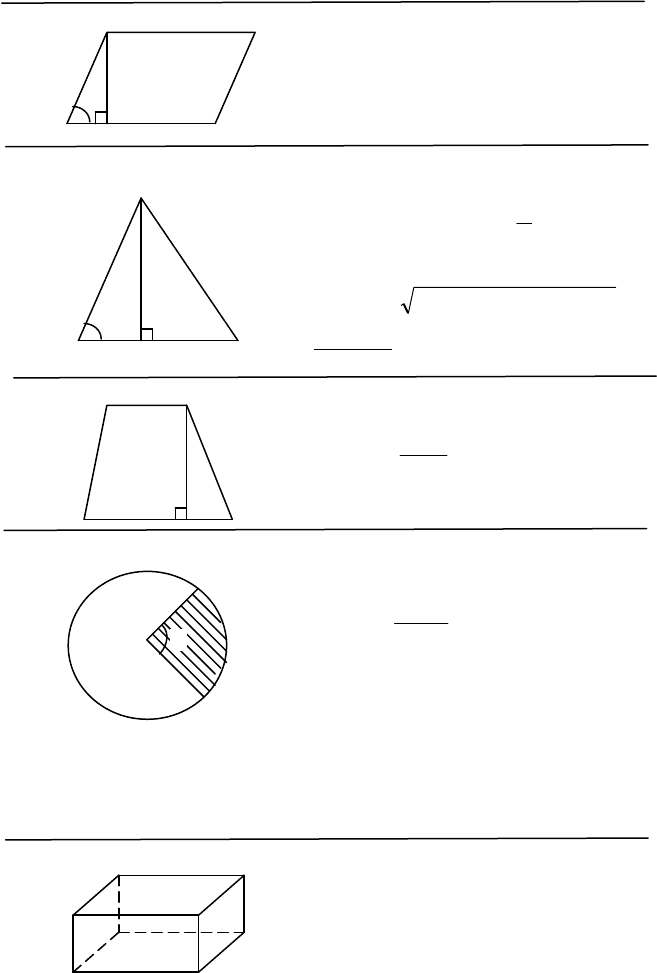
Формули площ фігур
Паралелограм
a
ahS =
; α= sinabS .
(для ромба ще і
2/ddS
21
×= ,
де
1
d і
2
d - його діагоналі).
Трикутник
2/ahS
a
=
;
γ= sinab
2
1
S
;
R4/abcS = ;
prS =
;
()()()
cpbpappS −−−= ;
2
cba
p
++
= .
Трапеція
h
2
ba
S ×
+
=
Круг
2
RS π= - площа круга;
360
R
S
2
απ
=
- площа сектора.
Стереометрія
Паралелепіпед
HSV
осн
×= ;
прямокутний:
abcV = ;
b
a
h
a
h
a
γ
b
a
c
b
a
h
O
α
R
b
a
c
