Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3

Подождите немного. Документ загружается.

§1.

Диференціальні рівняння першого порядку

г'-2±- =

Розв'язуємо це рівняння за допомогою підстановки Бернуллі

і = иу, 2' - и'у + иу :

и V + «у - 2 — = и У ,

1 2 2

V -2— =

V ,

иу + и

у'-2-

= 0,

' 2 2

иу = и V ;

З першого рівняння системи:

— = 2—; ІпМ = 2Іп|х|; У =

V X

З другого рівняння системи:

сій -,

•>

т ди

•

= и"у; — = и'х ; ——

V =2-,

и - и у.

ах;

-м +С, =—; И = ;—

З х

(тут перепозначили ЗС

]

= С ).

Отже,

С,

С-х^

ЗС,-х

С-х

Зх^

С-.

Тоді

Зх^

х С-х'

є загальним розв'язком заданого рівняння Ріккаті.

б) задане рівняння у' + 2у (у - х) =

є рівнянням Ріккаті "

/+/

(дг).у +

0(х);>>

=/(*),

де />(х) = -2х, £(х) = 2, /(*)=!.

Оскільки у

(х) = х є частинним розв'язком цього рівняння (перевір-

те!),

то заміна

У = У\ + 2 = Х + 2

зводить його до рівняння Бернуллі:

Глава 1. Диференціальні рівняння

г'

2(х

г)(х +г - х) - 1,

г'

2гх = -2г

Розв'язуємо

це

рівняння

за

допомогою підстановки Бернуллі

= иу,

г'=и'у

+ иу':

и V + иу +

2ИУХ

= -2г/ V ,

+ и(У +

2таг)

-2и

(V +

2УХ

= 0, \у =-2УХ,

' -> 2 2 1 ' т 2

[г/

V =

-2г/

V , I

- ~2и V.

З першого рівняння системи:

—

-2УХ, —

--2хйх,

1п

| =

—л:

у = е~

ах

З другого рівняння системи:

_2и

е-*\

-*і =

2е-*

ах,

и = І2

Іе^Ос

+ сУ .

ах

2 У 3

Отже,

_,2

= иу — є

}

е~

х2

ах

+ с)'.

Тоді загальним розв'язком заданого рівняння

є:

= х + г-х + е'"

(2$е~*

ах

+ с) .

Зауважимо,

що

загальний розв'язок рівняння представлено

квадра-

турах,

бо ^е~

ах не

виражається

елементарних функціях.

Диференціальні рівняння

повних диференціалах

та

звідні

до них

Приклад

13.

Розв'язати рівняння

(х

+ у +

сіх

+ (х - у

сіу = 0 .

• Задане рівняння

рівнянням

повних диференціалах вигляду

Р(х,у)ах

+ <2(х,у)ау = 0,

де

Р(х,у)

= х + у + \,

()(х,у)

= х-у

+3;

ар

, до , др до

— =1,

отже,

— = — .

ду

дх ду дх

Диференціальні рівняння першого порядку

Тому ліва частина заданого рівняння є повним диференціалом деякої

функції и(х,у):

(х + у + \)ах + (х-у

+ 3)ау = и(х,у).

Тоді рівняння зводиться до вигляду

сіи(х,у) = 0,

де и(х,у) - деяка функція, яку треба визначити.

Загальним розв'язком цього рівняння є

и(х,у) = С.

Для відшукання функції и(х, у) використовується два способи.

Спосіб 1. Оскільки

, ди , ди ,

аи = — ах-\ ау ,

дх ду

з заданого рівняння маємо:

ди ди ->

— = х + у + \, —~ = х-у- +3 .

дх ду

Інтегруємо перше з цих рівнянь по х :

и(х,у) = §(х + у+\)сіх =— + ух + х + ц>(у) .

Далі диференціюємо отриману функцію по у і прирівнюємо задано-

ди

му виразу для

ду

Звідси

Отже,

ди ,, . 7 .

— = х + ф(у) = х-у +3.

ду

<?'(у) = -у

+ 3,

фОО^-у+Зу+с.

2 З

X У , „

и(х,

у)-

— + ух + х- — + Зу + С .

2 З

Загальний інтеграл заданого диференціального рівняння

2 З

х у

— + ух + х- — + Зу = С.

2 З

Глава 1, Диференціальні рівняння

Спосіб 2. Для визначення и(х,у) застосуємо криволінійний інтеграл

другого роду

<.Х,У)

и(х,у)~

](х+у + \)ах + (х-у

+ 3)ау .

(.Хо.Уо)

За початкову точку (х

,у

) виберемо, наприклад, початок коорди-

нат. Шляхом інтегрування - ламану, зображену на рис. 1.4.

Тоді, переходячи до визначеного інтеграла, маємо:

и(х,у) - $х + $ах + Г(д:- у

+ 3)ау = — + х + ху- — + Зу + С .

О (х, 0) х

Рис.

1.4

Загальний інтеграл має вигляд

— + ух + х- — + Зу~С.<

2 З

Приклад 14. Розв'язати рівняння

(х

- \)ах + IX

у ау = 0.

• Перевіримо, чи є дане рівняння рівнянням у повних диференціалах:

Р(х,у) =

-1

<2(х,у)

= 2х^у,

Оскільки

ЗР

— = 2х у,

ду

~- = 6х у.

дх

ду дх

то задане рівняння не є рівнянням у повних диференціалах.

Проте права частина формули (1.47) має вигляд

1 (дР д£}\

-Ах

б (^у дх ) 2х

у х '

Диференціальні рівняння першого порядку

тобто залежить від х, тому рівняння має інтегрувальний множник ц, який

залежить лише від х: ц = д(;с) •

Складаємо рівняння (1.46) і розв'язуємо його:

йПпц _ 2

ах х '

1пц = -21п|х| + Іп|С|;

Ц = -^-, СФО.

Нехай С = 1, тоді ц = •

Помножимо обидві частини заданого рівняння на ц = —у. Дістанемо

рівняння у повних диференціалах:

йх

+ 2ху

Оу

= 0,

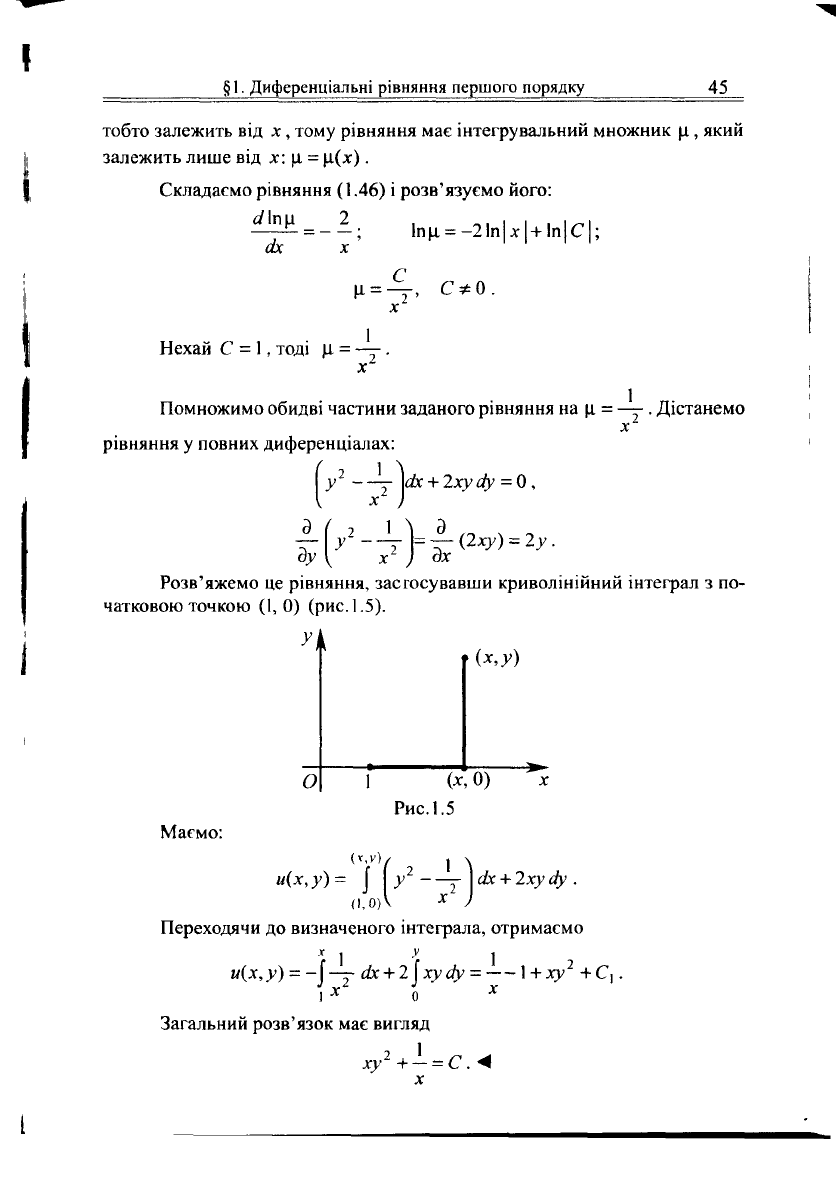
Розв'яжемо це рівняння, застосувавши криволінійний інтеграл з по-

чатковою точкою (1, 0) (рис. 1.5).

* (х,у)

1 (х, 0)

Рис.

1.5

Маємо:

ах + 2ху ау .

и(х,у)= \ \у

(1,0)4

Переходячи до визначеного інтеграла, отримаємо

и(х, у) = -|—— ах + 2§ ху

Оу

= —-\+ху

+С).

Загальний розв'язок має вигляд

ху

+- = С.<

Глава

Диференціальні рівняння

Диференціальні

рівняння,

нерозв'язні відносно

похідної

Приклад

15.

Розв'язати

рівняння,

нерозв'язні відносно

похідної

а)

у'

+ху'-х;

6)х

у'

+—,.

•

а)

задане рівняння

у = у'

+ху'-х

є рівнянням вигляду

= /О,/),

де

У(х,у') = у'

+ху'-х.

Введемо параметр

—

у .

Тоді, підставляючи

задане рівняння, масмо

у = р

+х(р-\).

Диференціюємо

цю

рівність

по х :

„

Ф Ф

р =

2р-£-+

р-\+х-^,

ах ах

—

(2р + х) = \, — = ,

ах ах 2р + х

ах „ ах

-—

= х + 2р, -—х = 2р.

ар ар

Це рівняння лінійне відносно

х та х'.

Розв'язавши

це

рівняння, маємо його загальний розв'язок (перевірте!):

х =

Се

-2{р

+ \).

Враховуючи,

що у= р

+х(р-\),

маємо

у = р

+ (Се" -2(р + \))(р -1) = Се"

(р-1)-

+ 2 .

Отже,

загальний розв'язок вихідного рівняння записується

парамет-

ричній формі:

х =

Се

-2(р

+ \), у =

Се

(р-\)-р

+2.

б) задане рівняння

х =

+—,

§ І. Диференціальні рівняння першого порядку

є рівнянням вигляду

Де /(у,/) = /

+Л-

х =

/(у,у),

Введемо параметр р

—

у'. Тоді, підставляючи в задане рівняння, маємо

і у

х-р-

+ — .

Диференціюємо цю рівність по у та врахуємо, що — = -—

ау ау^

сіх

сір

р-у—

1 _

„ Ф . Ф

Р Ф Р

або

Звідки

Маємо

= 2/

,Ф

1__І1Ф

Р Ф Р р' Ф

= 0.

= 0; 2р--^ = 0

7 У 1

Враховуючи, що х = р н—, маємо у = хр-р' . Підставимо замість

р їх значення. Тоді отримаємо:

при р\ -С загальний розв'язок у^хС-С

;

,[7

при р

= у— маємо:

Глава 1. Диференціальні рівняння

2 З

2 2 з 2 т

Зл/3

Розв'язок у = —х

є особливим.

Зл/З

Отже, розв'язками вихідного рівняння є

Зл/З

Приклад 16. Розв'язати рівняння

у = 2ху - у .

• Задане рівняння є рівнянням Лагранжа:

у = х<р(у') + у(/).

Введемо параметр р — у\ тоді

у ~ 2хр - р

Диференціюючи, отримуємо

^ т Ф - 2 Ф

р = 2р + 2х—-3р —

або

^(-2х + 3р

) = р

... ф .

і після ділення на —— дістанемо рівняння

ах

ах „ і

/> — = -2х + 3/7".

Інтегруючи це лінійне рівняння (див. приклад 9), маємо:

С 3

(перевірте!).

Отже, інтегральні криві визначаються рівняннями

у = 2хр-р , х = — + -р

При діленні на — губимо розв'язок р = 0 рівняння

ах

§1.

Диференціальні рівняння першого порядку

^-(-2х + 3р

) = р,

ах

якому згідно з рівнянням

у = 2хр- р

відповідає розв'язок у - 0 вихідного рівняння. Л

Приклад 17. Знайти розв'язок рівняння

' '2

У = ху - у .

• Задане рівняння є рівнянням Клеро:

у = ху' +

у(у').

Скористаємось вказаним у теорії практичним правилом. Загальний

розв'язок цього рівняння, згідно з формулою (1.61)

у = Сх + у(С),

має вигляд

у = Сх-С

Особливий розв'язок заданого рівняння дістанемо, виключаючи далі

параметр С з системи рівнянь:

\у = хС-С

\о = х-2С

(друге рівняння системи отримано диференціюванням обох частин першого

рівняння системи по лс).

Звідки отримаємо у = особливий розв'язок.

Це рівняння обвідної сім'ї прямих у = Сх-С (рис. 1.6).

Рис.

1.6^

Глава 1. Диференціальні рівняння

Задачі геометрії

Приклад 18. Знайти рівняння кривої, яка проходить через

точку (1,1), якщо для кожного відрізка

[1,

д:]

площа криволіній-

ної трапеції, яка обмежена відповідною дугою цієї кривої, вдві-

чі більше добутку координат точки М(х, у) кривої (х > 0, у > 0).

• Згідно з умовою задачі маємо

)У(і)<іі =2ху(х) .

Диференціюючи цю рівність по х, отримуємо диференціальне рівняння

у = 2(у + ху')

або

2х

Проінтегруємо це рівняння та врахуємо початкову умову у(\) =

ау _ 1 г ах

V ~~2 •'Т'

1п|у| = -11п|х| + 1пС,

у = -^=, Я0 = С = І.

Л/Х

Отже, маємо рівняння шуканої кривої:

Приклад 19. Знайти всі лінії, у яких піддотична пропор-

ційна абсцисі точки дотику (коефіцієнт пропорційності дорів-

нює к).

• Нехай у = /(х) - рівняння однієї з шуканих кривих. За умовою

задачі запишемо, що піддотична та абсциса х пов'язані так:

5, = Ах.

Використаємо формулу для довжини дотичної

і отримуємо відразу диференціальне рівняння