Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§2.
Власні вектори та власні значення
181
Підставимо послідовно А\ та Я
2
в записану систему.
1.
Вважаємо Я] = 3. Отримуємо однорідну систему, у якій два рівняння
еквівалентні, і тому розв'язання її виконується так:
|-2х] + 2х
2
= 0 ; .
( —Х\ + х
2
=
0
,
^
2х\ -2^2=0,
х, -х
2
Х2 = С
X] =с ;
Х2 = с .
Прийняли, що X) - базисна змінна,
Х2
- вільна змінна, та перепозна-
чили вільну змінну х
2
= с .
Загальний розв'язок однорідної системи
Х(с) =
сєК .
Сукупність власних векторів, що відповідає власному значенню Я)
х
(Я|)
=(с, с) =
с(1,
1), сєК, с*0.
2.
Вважаємо Я
2
=-1. Однорідна система рівнянь для визначення
власного вектора х^
2
-* розв'язується аналогічно попередньому.
[2х, +2х
2
=0 ;
І2х, +2х
2
=0 ,
Хі +х-> = 0 ,
х, = -х
2
х
2
= с
х і =
—с
;
х
2
= с .
Загальний розв'язок однорідної системи
сєК.
•Мі)
Сукупність власних векторів, що відповідає власному значенню Я
2
(-с, с) = с(-1,1), сєК, с*0.
Отже, маємо: Я,=3,
Я
2
=-1;
х
(Л|)
= с(1,1), х
(Яз)
= с(-1, 1),
сєК , с*0.
Приклад 2. Знайти власні значення і власні вектори
лінійного оператора <Л, що заданий матрицею А .
ґ
2 0 -1
Л
А= 11-1
1 0
ч

182
Глава
5.
Лінійні оператори
•
Характеристичне рівняння
2-А 0
1
-1
1-А -1 =0.
1 0 2-А
Розкривши визначник, отримаємо
(1-А)((2-А)
2
-1)
= 0 ;
(1-А)
(1-А) (3-А) = 0 ;
(1-А)
2
(3-А) = 0;
А]
= А
2
—
1
, А
3
= 3 .
Маємо: корінь Х.
1
=1
—
кратний, показник кратності к = 2 , корінь
А-з = 3
—
простий, к = 1.
Система рівнянь для визначення власних векторів має вигляд
(2-А)Х,
-*
3
= О;
Хі +
(і
-
А)Х
2
-
х
з
=
о
;
-х,
+
(2-А)х
3
=0.
Підставимо послідовно X., і Л-з в записану систему.
1. X] = 1, к = 2 . Система приймає вигляд:
X]
- х
3
= 0 ;
X]
- х
3
= 0 ;
-
хі + х
3
= 0 .
Розв'язуємо систему методом Гаусса.
'
1 0
-Г
'1
0
_1
1
А-А
І
Е
= 1 0
-і
0
0
0
V"
1
0
0
г
=
К%(А-А
х
е)=і
=> аітГІ = п-г = 3-1 = 2 => 3 два лінійно
незалежних власних вектора, що відповідають власному значенню А|.
Скорочена система рівнянь приймає вигляд
{
X)
—
х
3
= 0
,
=>
{
х, = х
3
.
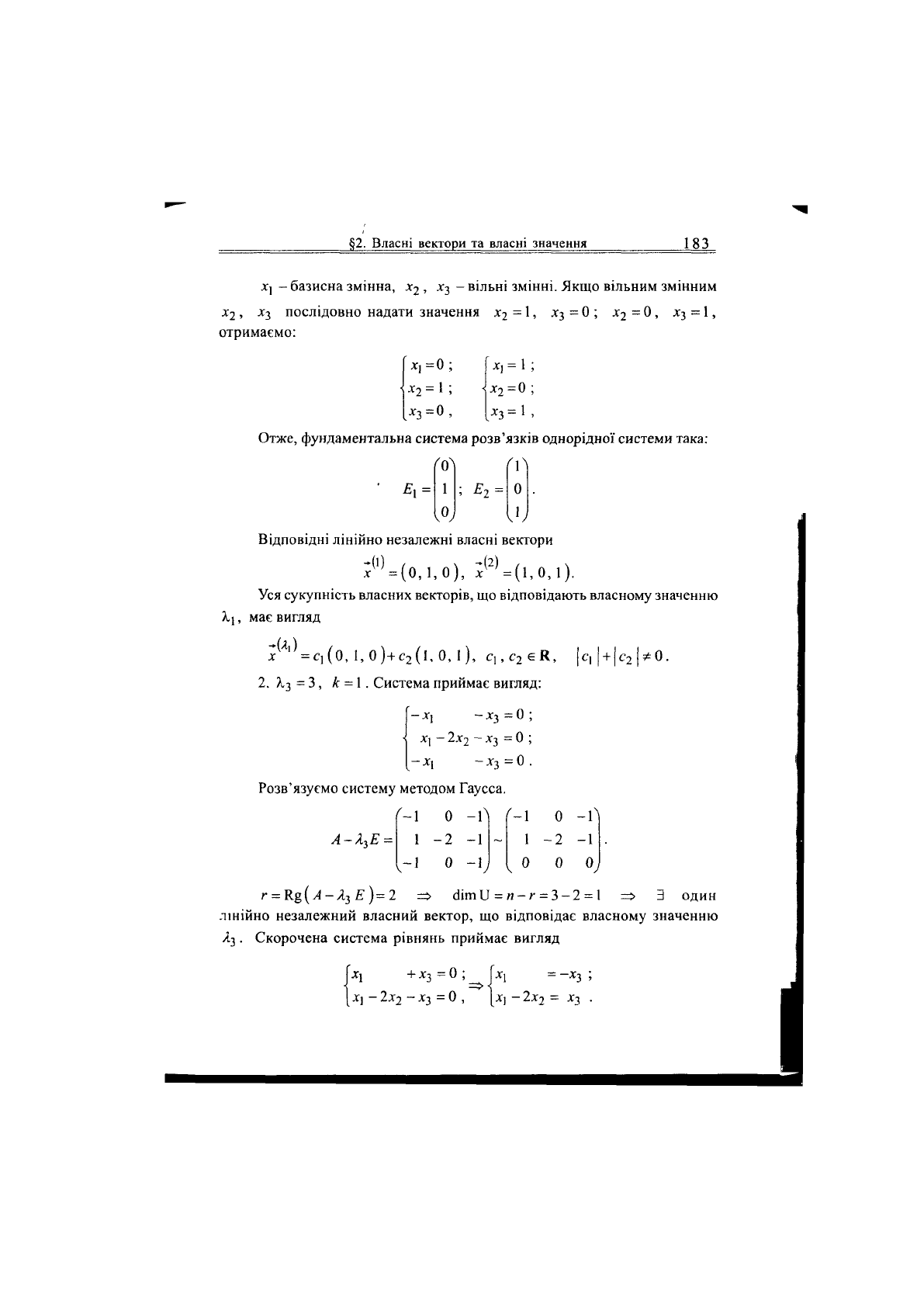
§2.
Власні вектори та власні значення
183
х
{
- базисна змінна, х
2
, х
3
- вільні змінні. Якщо вільним змінним
х
2
, х
3
послідовно надати значення х
2
= 1,
отримаємо:
х
3
= 0 ; х
2
- 0 , х
3
= 1,
X] =0 ;
х
2
= 1;
х
3
= 0 ,
X] = 1
х
2
=0
х
3
= 1
Отже, фундаментальна система розв'язків однорідної системи така:
'°1
1
; е
2
=
0
Л
Відповідні лінійно незалежні власні вектори
х
(і)
= (0,1,0), х
(2)
= (і,0,і).
Уся сукупність власних векторів, що відповідають власному значенню
А.),
має вигляд
х
=с,(0, 1, 0)+с
2
(і, 0, 1), с,, с
2
єК,
2.
А,
3
= 3, к = 1. Система приймає вигляд:
- X] - х
3
= 0 ;
х,
—
2х
2
—
х
3
—
0 ;
-х,
-*
3
=0.
Розв'язуємо систему методом Гаусса.
с, + с
2
*0.
'-1
0
-Г|
Г-1
0
-Г]
1 -2 -і
1
-2
-і
,-1
0
-ь
,
0
0
г = К§(/1-Д
3
£)=2 => (Ііт II = и-г = 3-2 =
1
=> 3 один
лінійно незалежний власний вектор, що відповідає власному значенню
/і
3
.
Скорочена система рівнянь приймає вигляд
X} + х
3
= 0 ;
X]
—
2х
2
—
х
3
= 0 ,
х
\ -
—хт,
;
Х|
—
2х
2
= х
3
.

184
Глава 5. Лінійні оператори
Фундаментальна система розв'язків одержується, якщо покласти
х
3
=1:
=-і;
х
\ =
-1
Х\ - 2х
2
=
1
;
=>
х
2
=
-1
*з=
1
>
х
3
=
1
' 1
л
-(з)
Відповідно власний вектор х =(-1,-1,1). Уся сукупність власних
векторів, що відповідають власному значенню Х
3
, має вигляд
-(Яз
=
с(
—1, —1,
1), сєК, с*0.<*
Приклад 3. У комплексному просторі £
3
знайти власні
вектори та власні значення лінійного оператора, що зада-
ний дійсною матрицею:
( 4 -5 7^
А= 1-4 9
,-4 0 5
у
• Знаходимо власні значення, розв'язуючи характеристичне рівняння:
4-А -5 7
1 -4-А 9 =0.
-4 0 5-А
Після перетворень характеристичне рівняння приймає вигляд:
4-А -5 -29 + 9Я
1 -4-А 0 =0.
-4 0 41-Я
Розкривши визначник, отримаємо:
X
3
-5Х
2
+17Х.-13 = 0.

§2.
Власні вектори та власні значення
185
або
(Л-і)(/1
2
-4Л + 1з)=0;
Я.,
=1; і
23
=2±3/.
Запишемо систему рівнянь, з якої визначаються власні вектори.
'(4-Л)х,- 5х
2
+ 7х
3
=0 ;
X]-(4
+ Я)х
2
+ 9х
3
=0 ;
-4х!+ (5-Д)х
3
=0.
Покладемо А = А\ = 1. Система прийме вигляд:
Зх] -5х
2
+7х
3
=0 ;
X]
-5х
2
+9х
3
=0 ;
-4х,+ 4х
3
= 0.
Розв'язуємо систему методом Гаусса.
( 3
-5
7^
0
п
/
-1 0
Г
-1
о
Г
А-А
Х
Е
=
1 -5 9 ~ 1
-5 9
0 -5 10 0
-1 2
0
V
3
-5
7
,
V
0 -5
0
о
°,
-Я|£)= 2 ; сПтІІ = 3-2 =
1
=> 3 один лінійно незалежний
вектор, що відповідає X].
Запишемо скорочену систему:
-Х| + х
3
=0 ;
-х
2
+2х
3
=0 ,
X] - х
3
;
х
2
=
2
х
3
,
х
2
=2 ;
х
3
=
1
.
Фундаментальна система розв'язків: Е\ ; х = (і,2,і)-
влас-
ний вектор, х^ = с(і, 2, 1), сєК, с*0 - сукупність
торів,
що відповідають власному значенню Х\ = 1.
Покладемо А = А
2
= 2 + Зі.
власних век-
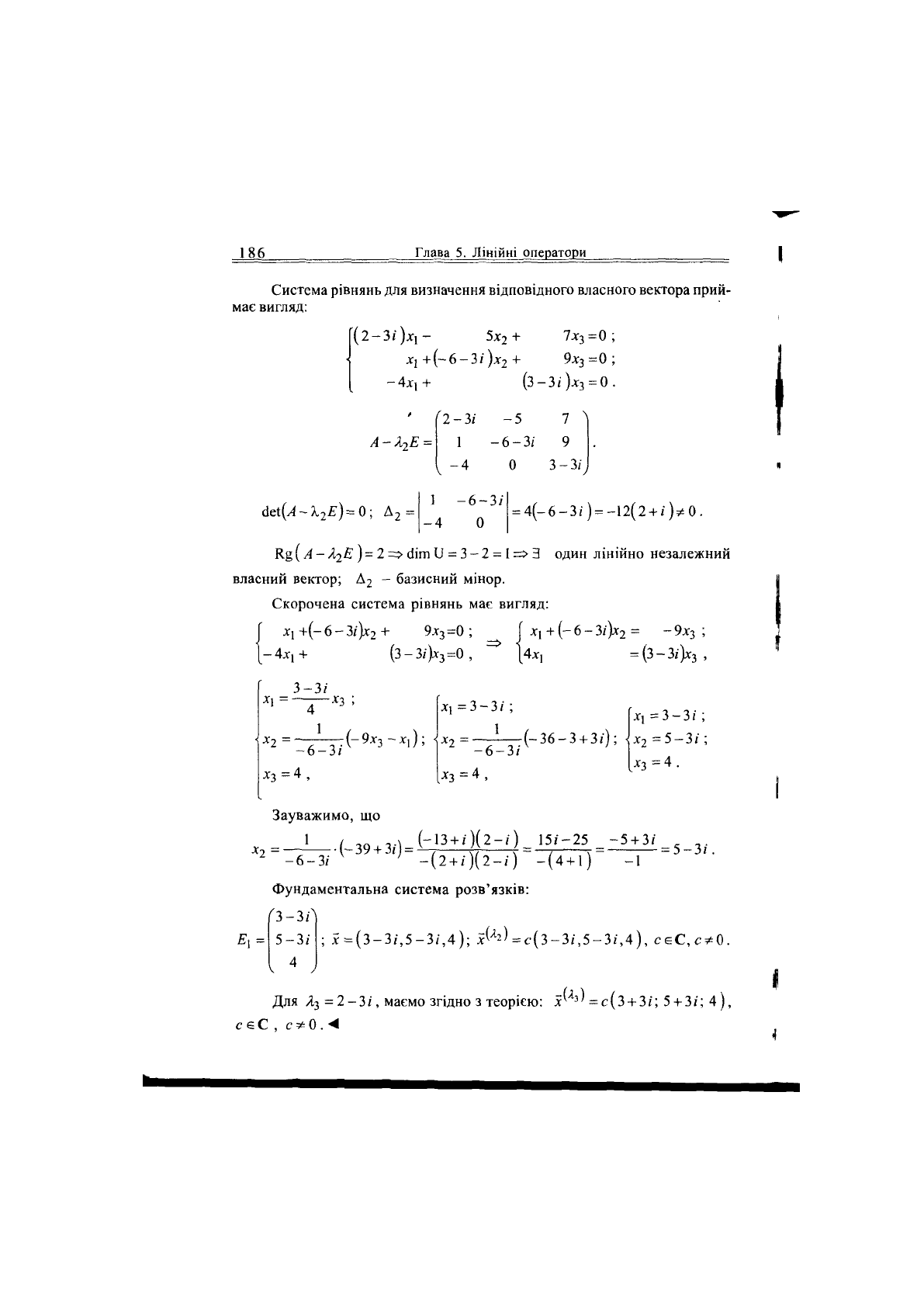
186
Глава 5. Лінійні оператори
Система рівнянь для визначення відповідного власного вектора прий-
має вигляд:
(2 -
31"
)дгі - 5*
2
+ 7*3=0;
хі +(-6-3/)х
2
+ 9*з=0;
-4*1+
(3-3/)*з = 0.
А - Я
2
Е =
2-3/
-5 7
л
1 -6-3/ 9
ч
-4 0 3-3/,
<1єі(А~Х
2
е)--=0;
д
2 =
:4(-6-3/) = -12(2 + /)*0.
1 -6-3/
-4 0
К§(Л-/І2£
,
)=2=>олти
= 3-2 = 1=>3 один лінійно незалежний
власний вектор; Д
2
- базисний мінор.
Скорочена система рівнянь має вигляд:
Г *!+(-6-3/)*
2
+ 9*з=0; [ *і
+(-6-3/)*2
= -9*з ;
1-4*і+
(3-3/)*з=0, [4*, = (3-3/)*
3
*1
*
2
3-3/
-*3
;
1
-6-3/
*
3
= 4 ,
Зауважимо, що
1
:(-9дг
3
-*і);
*і =
3
-
3
/
;
1
х
2
= (- 36 -
3
+
3
/);
•6-3/
*
3
= 4 ,
*і =
3
-
3
/;
*2
=
5
- 3
/;
*
3
= 4 .
*
2
=
(-39
+
3/)
=
1=І1±4
2
^
=
І^
= ^1ІІ
=
5-3/.
1
-6-3/ ' -(2 + /)(2-/) -(4 + 1) -1
Фундаментальна система розв'язків:
ґз-зЛ
Е
х
= 5-3/ ; *=(3-3/,5-3/,4); *^ = с(3-3/,5-3/,4), сєС,с*0.
I
4
,
Для Я
3
= 2-3/, маємо згідно з теорією: *^ =с(з + 3/; 5 + 3/; 4),
сєС,с*0.<

§2. Власні векюри та власні значення
187
Приклад
4. Звести матрицю А =
тора
о4 до діагонального вигляду.
1
2^
2
4
лінійного
опера-
•
Визначаємо власні вектори та власні значення матриці А. Для цьо-
го складаємо характеристичне рівняння
1-А 2
2 4-А
0,
(і-А)(4-А)-4 = 0,
А
2
-5А=0,
А(А-5)=0,
А, = 0, А
2
= 5.
2
Оскільки власні значення різні, то існує базис у К з власних век-
торів, а матриця оператора в цьому базисі (новому) має діагональний виг-
ляд. У даному випадку
'0 0
Л
Далі впевнимося в цьому, переходячи до нового базису з власних век-
торів за допомогою матриці переходу Т.
Власні вектори знаходимо з системи рівнянь (А-
А
Е)Х = 0, тобто
(і-А)*,+ 2*2=0;
2х, +(4-А).х
2
=0 •
Покладемо А = А. = 0.
ЛЇ
+2*2=0 ;
х
\ - -
2*2;
[2
лг)
+4х
2
=0 , [х
2
= 1 ,
*(') = (- 2, 1) - власний вектор, що відповідає Л
{
.
Покладемо А = А
2
= 5.
[-4хі+2д:
2
=0;
[*
2
=2*|
;
[ 2х
х
- *
2
=0 , [*,= 1 ,
х^ = (1, 2) - власний вектор, що відповідає А
2
.
*1
=
-
2 ;
*
2
= 1.
•V,
= 1;
*2
= 2 .

Оскільки вектори х^ лінійно незалежні, вони утворюють ба-
зис у К .
Матриця переходу Т від старого базису до нового (з власних век-
торів) така, що її стовпцями є власні вектори, тобто
Т =
-2 1
1 2
Тоді А' = Т~
]
АТ
2 -1
•1 -2
А =•
ґ
2 2
-1 -2
1 о
5-5
-10
ґ
-2 У
2 4
_]_
5
У
'0 о
,0 -25
Л
'о о^
о 5
V
4
Таким чином, безпосередньо перевірили, що матриця лінійного операто-
ра у базисі з власних векторів має зазначений діагональний вигляд.
Приклад 5. Звести матрицю А лінійного оператора до
діагонального вигляду та знайти відповідний базис, якщо
' 1
0
-2
• Характеристичне рівняння
1-А 2
йеі(А-АЕ) =
0
-2
2-А
-2
2
2
2
0
0
-1-А
0
Л
0
= (А-2)(і-А
2
)=0
має корні Я
х
= 2 , А
2
= 1, А
3
= -1. Оскільки власні значення різні, то
існує базис у К з власних векторів лінійного оператора. Отже, матриця
може бути зведена до діагонального вигляду.

§2,
Власні вектори та власні значення
189
Знаходимо відповідні власні вектори з системи рівнянь
(А-
ЛЕ)Х = 0.
Якщо /1=2, система прийме вигляд
ґ-1
2
°1
х
\
{А-2Е)Х
= 0 0 0
х
2
=
0
,-2
-2
-з,
І»,
або
-
X] + 2*2 = 0 ;
-
2х] - 2х
2
-Зх
3
= 0 .
Фундаментальна система розв'язків складається з одного розв'язку
'
2^
ч-2у
;
власний вектор х^'^ = (2,1,-2).
Аналогічно, якщо Л =
1
система прийме вигляд
(А-Е)Х
=
ґ
0
0
2
2 0
1 0
-2 -2
х
2
V
0
У
або
х
2
=0;
-2*1 -2*2 -2*3=0 ,
х
2
=0;
Х\
+х
2
+х
3
=0.
З цієї системи знаходимо другий власний вектор і'
2
' = (і,0,-і).
Нарешті, якщо Я =
-1,
власний вектор
х^^
= (0, 0, 1).
Знайдені вектори х
х
, х
2
, *з лінійно незалежні, отже, утворюють
базис, в якому матриця лінійного перетворення А має такий діагональний
вигляд
ґ
2 0 0
Л
0 1 0
0 0-1
Перевіримо це.

190
Глава 5. Лінійні оператори
Сформуємо матрицю переходу Т з власних векторів (розташовуємо
їх стовпцями).
1 0
1 о о
-2 -1 1
, аеіГ =
-1,
А =
Т~
1
АТ,
г-Ч-і)
0 -1 -0
-12 0
0 0-1
= (-1)
Го і о
ч
(
А'
=
1 -2
0
,1
0
Ь
V
1 2
0 2
2 -2
0 -1
-1 2
-1 0
оу 2
0
-1,
'0
і
0^
=
1 -2
0
)
,1 0
К
1
°1
0 0 =
-1
У
2 0
2 0
0 -1
\
Г
2
1
о
ч
(2
0
°ї
1
0 0
=
0
1 0
/
,-
2
-1
,0
0
-1
Приклад 6. Знайти власні вектори та власні значення
лінійного оператора сЛ, що заданий в деякому базисі матри-
цею А. Чи зводиться ця матриця до діагонального вигляду?
0 -4
0
1 -4 0
1 -2
-2
• Знаходимо власні значення з характеристичного рівняння
-Я -4 0
1 -4-Я 0
1 -2 -2-А
= 0.
