Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§2,
Власні вектори та власні значення
191
(-2-А)(л(4 + Л) + 4)=0,
(Л + 2)(л
2
+4А + 4)=0,
(Я + 2)
3
=0.
Я = -2, показник кратності
А:
= 3 . >
Запишемо систему рівнянь для визначення власних векторів.
-Лх\- 4х
2
=0; [Ях] + 4*2 =0;
| X] +(- 4 -
Я
)х
2
=0 ; => І X] -(4 +
Я
)х
2
=0 ;
*! - 2х
2
+ (-2-Я)х
3
=0, X)- 2х2-(2 + Я )х
3
=0.
Покладемо Я = -2 .
-2х| +4х
2
=0 ;
Х|
-2х
2
=0 ;
Х|
-2x2=0 .
/• = К.§(Л-Я£)=1; сііт Іі = «-/- = 3-1 = 2 => 3 два лінійно неза-
лежні власні вектори, що відповідають Я = -2 .
Скорочена система:
{*! -2х
2
=0, {х, =2х
2
.
X]
- базисна змінна, х
2
, х
3
- вільні змінні; х
2
= , х
3
= с
2
.
Знаходимо фундаментальну систему розв'язків.
Х\=2с
]
;
х,=2 ;
-і=0;
х
2
= с, ; •
х
2
=1;
•
х
2
=0 ;
х
3
= с
2
,
х
3
=0 , х
3
= 1.
х'
1
' = (2,1, 0), х'
2
' = (0, 0,1) - лінійно незалежні власні вектори.
Вся сукупність власних векторів:
х^=с,(2, 1, 0)+с
2
(0, 0, і),
с,,с
2
єК,
|с,
|
+
|с
2
|*0.
Матриця А не зводиться до діагонального вигляду, бо не існує повного
набору власних векторів, тобто вектори х^
1
\ х^
2
^
- лінійно незалежні, але
вони (їх два!) не утворюють базис тривимірного простору.
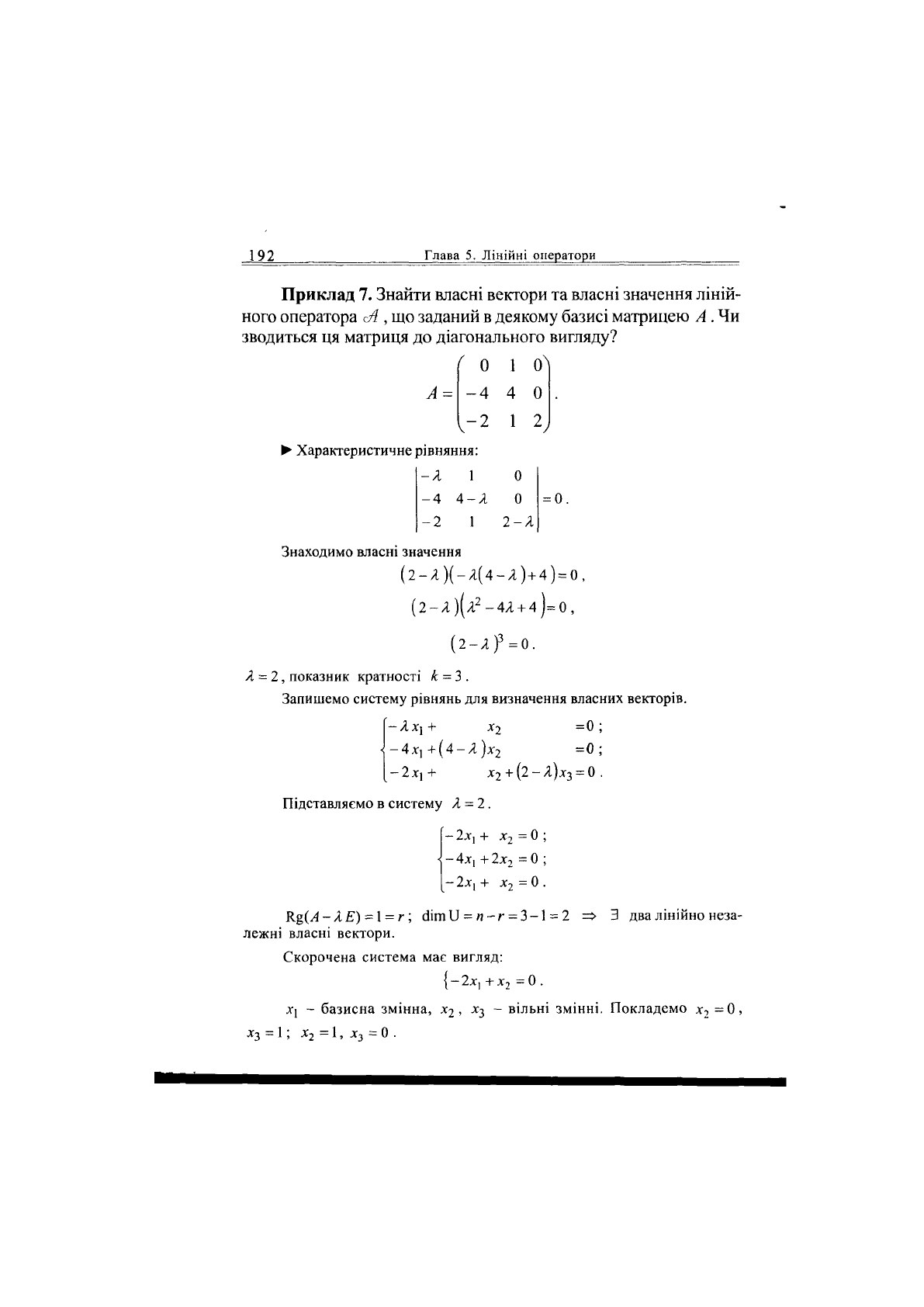
192
Глава 5. Лінійні оператори
0 1 0
-4 4 0
-2
1 2
Приклад 7. Знайти власні вектори та власні значення ліній-
ного оператора сА , що заданий в деякому базисі матрицею А
.
Чи
зводиться ця матриця до діагонального вигляду?
А =
V
• Характеристичне рівняння:
-А 1 0
-4 4-А 0
-2 1 2-А
Знаходимо власні значення
(2-А)(-А(4-А) + 4)=0,
(2-А)(а
2
-4А + 4)=0,
(2-А)
3
=0.
А = 2, показник кратності к = 3 .
Запишемо систему рівнянь для визначення власних векторів.
—
А
X] + х
2
= 0 ;
\-4х] +(4-А )х
2
=0;
-2х,+ х
2
+ (2-А)х
3
= 0.
Підставляємо в систему А = 2.
-
2х, + х
2
0 ;
-4х, +2х
2
= 0 ;
-2х, + х
2
= 0 .
Кц(А-ЛЕ)
= \ = г;
йітії
= п-г = 3-1 = 2 => 3 два лінійно неза-
лежні власні вектори.
Скорочена система має вигляд:
{-2х, +х
2
= 0 .
Х[
- базисна змінна, х
2
, х
3
- вільні змінні. Покладемо х
2
= 0,
х
3
= 1; х
2
= 1, х
3
= 0 .

§2.
Власні вектори
та
власні значення
193
х\
=0 ;
х
2
=0; ^=(0,0,1);
х
3
=
1
,
-2=1;
х
2
=(-,1,0).
-з=0,
х
(і)
=
Сі
(0,0, 1) +
с
2
(-,1,
0), с„с
2
єК, |с,| + |с
2
|*0.
Матриця А не зводиться до діагонального вигляду, бо не існує бази-
су, складеного з власних векторів (вимірність простору дорівнює трьом, а
лінійно незалежних власних векторів два). -4
IV.
Задачі
для
практичних занять
5.34.У деякому базисі простору £ задані вектори
х,, х
2
, х
3
та матриця А оператора с4. Використовуючи оз-
начення, встановити, які з даних векторів є власними векто-
рами оператора <А, та знайти їх власні значення, якщо:
ґ
2 3}
х,=(і,3), х
2
=(3,і), х
3
=(5,0);
а) А =
0 З
ґ
-3 11
б) А =
7^
0 5-4
0 1 1
х,
= (3,0,0), х
2
=(0,-2,0),
х
3
=(і,0,-і);
ґ
5 9 7
Л
в) А
0 3-2
0 2-1
= (-4,1,1), х
2
=(2,0,0),
х
3
=(0,0,2).
5.35. Знайти характеристичне рівняння та спектр опера-
тора сЛ, який задано матрицею А в деякому базисі, якщо:
а) А
1 -2
1 4
б) А =
З 1
1 З
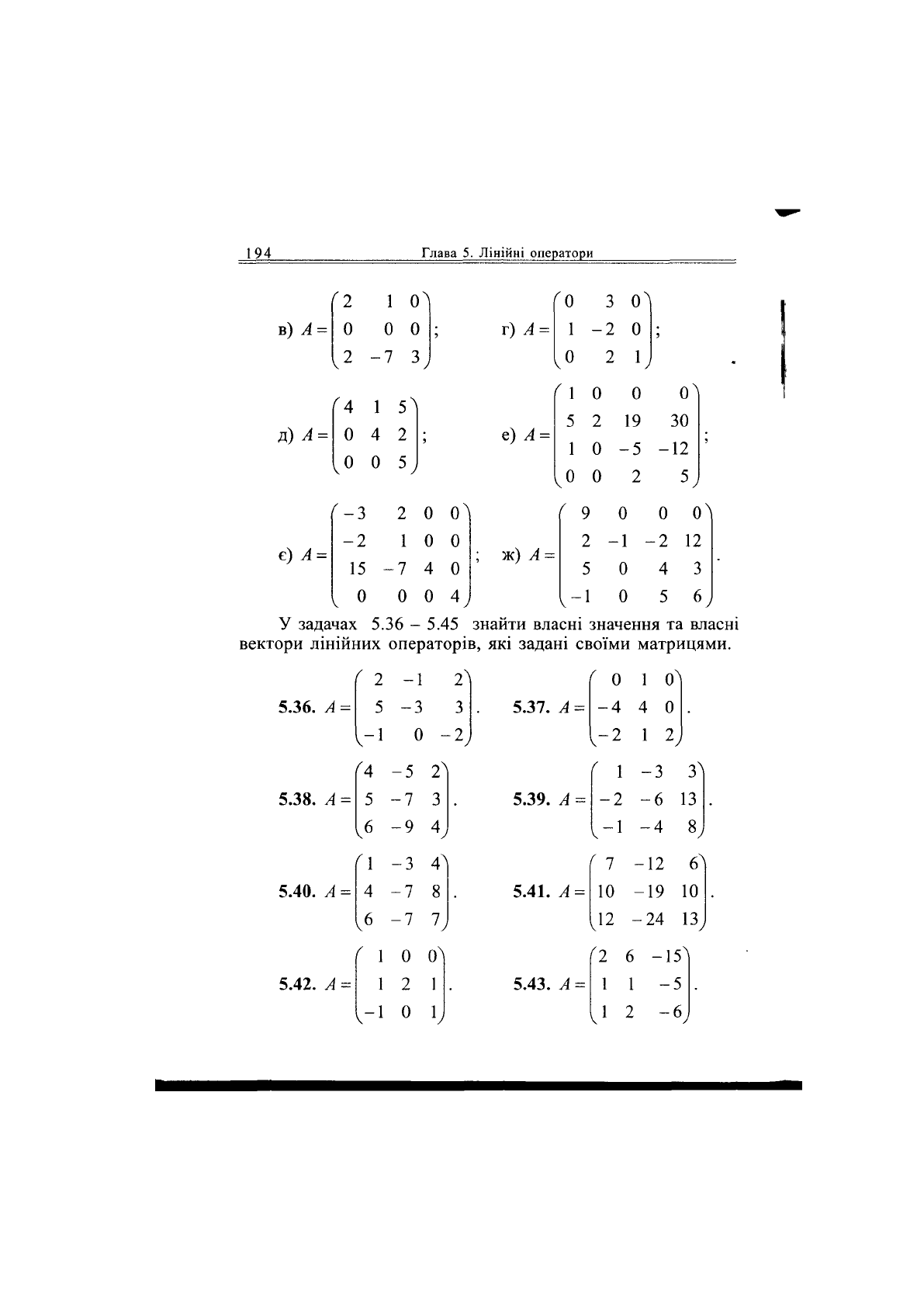
194
Глава 5, Лінійні оператори
в) А =
2 1 0
0
0
0
2 -7 3
г) А =
г
4 1
5
1
Д)А =
0 4 2
5,
2 0
-2 1 0
0
є) А = є) А =
15 --7 4 0
0 0
4,
е) А =
0
3
1 -2
0
0 2
Ь
1
0 0
0
5
2
19
зо
1 0
-5
-12
0 0 2 5
ж) А =
9 0
2 -1
5 0
-1 0
0 0^
-2 12
4
5
У задачах 5.36 - 5.45 знайти власні значення та власні
вектори лінійних операторів, які задані своїми матрицями.
5.36. А
' 2
5
V
•1
-1
•З
0
2^
З
•2
5.37. А
0
4
•2
1 0^
4 0
Г4 -5
2^
( 1 -3 3]
5.38. А = 5
-7 3
5.39. /4
=
-2
-6 13
,6
-9 4 -4
V
^1 -3
4
Л
' 7 -
-12 6)
5.40. Л =
4
-7 8
5.41.
А
=
10 --19 10
-7
^2 -
-24 13,
Г і 0
°)
(2 6 -15]
5.42. А =
1 2 1
5.43.
/4
=
1 1
-5
,-1
0
1
^
2
-6,
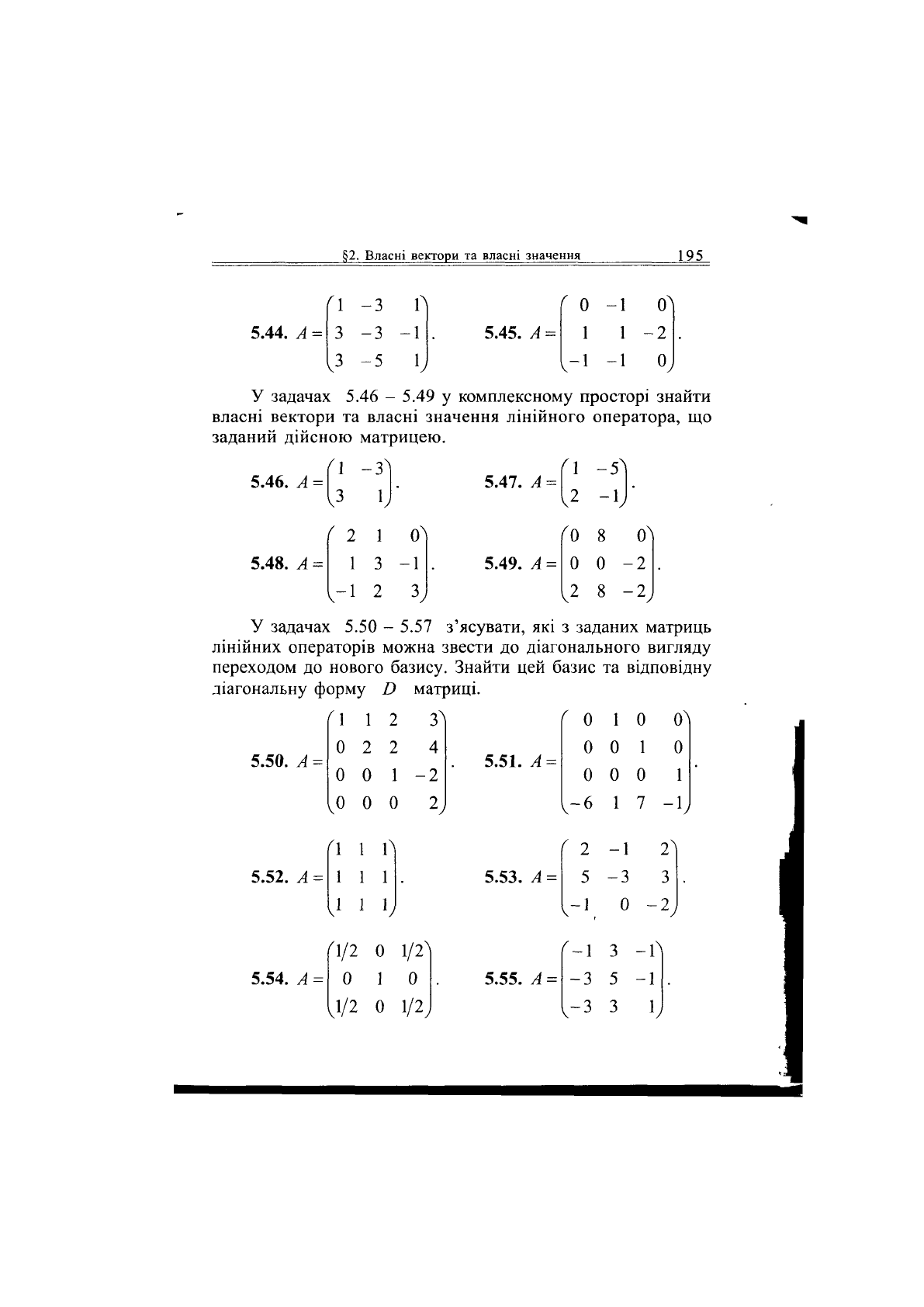
§2.
Власні вектори та власні значення
195
5.44. А =
1 -З
З -з
3 -5
5.45. А =
V
0 -1 о
1 1 -2
-1 -1 0
У задачах 5.46 - 5.49 у комплексному просторі знайти
власні вектори та власні значення лінійного оператора, що
заданий дійсною матрицею.
5.46. А =
5.48. А
1 -З
( 2
1
V-!
1 (0
з -і
2 Ь
5.47. А
5.49. А =
п
,2
'0
0
ч2
-5"
"І
8 0Л
0
-2
8 -2
У задачах 5.50 - 5.57 з'ясувати, які з заданих матриць
лінійних операторів можна звести до діагонального вигляду
переходом до нового базису. Знайти цей базис та відповідну
діагональну форму Б матриці.
3^
5.50. А
1 1
0 2
0 0
0 0
2
2 4
1 -2
0 2
5.51.
А
5.52. А =
5.54. А
ґ
\ 1 1
Л
1 1 1
ч
1 1 1,
'1/2 0 1/2
Л
0 1 0
0/2 0 1/2
у
5.53.
А =
5.55. А =
0 1 0 0
0 0
1
0
0
0 0 1
-6 1 7 -1
2 -1
2
1
5
-3
3
-1 0
2,
-1 3
-Г|
-3 5 -і
-3
3
1

196
Глава 5. Лінійні оператори
5.56. А
1
1
1
1 1
1 -1 -1
•1 1 -1
•1 -1 1
Гї
5.57. А
'о о о Г\
0 0 10
0 10 0
ч
1 о о о
У задачах 5.58-5.61 знайти ортонормований базис з влас-
них векторів та діагональну матрицю й в цьому базисі для
лінійного оператора, який задано в деякому ортонормованому
базисі матрицею А (шуканий базис визначається неоднозначно).
{
П
2
~
8
1
Г 17
-8 4
5.58. А = 2 2 10 5.59. А =
-8 17
-4
10
1
4
-4
11
Гз
—
/
о
4
(\ 1
2
1
5.60. А = і 3 0
5.61.
А =
1 1
2
0
у
2 2
\
У задачах 5.62 - 5.67 виконати вказані доведення.
5.62. Довести, що для невиродженості оператора А
необхідно та достатньо, щоб він не мав власного значення,
що дорівнює нулю.
5.63.
Довести, що якщо оператор сЛ невироджений, то
с/1
та сА'
х
мають однакові власні вектори. Знайти зв'язок
між власними значеннями цих операторів.
5.64. Довести, що оператор Л - $ при будь-якому А\
має ті ж самі власні вектори, що й оператор А . Знайти зв'язок
між власними значеннями цих операторів.
5.65. Довести, що власні значення діагональної матриці
співпадають з її діагональними елементами.

§3.
Лінійні оператори у евклідовім просторі
197
5.66.
Довести, що характеристичний многочлен транс-
понованої
матриці А
т
співпадає з характеристичним мно-
гочленом
матриці А.
5.67.
Нехай х та у - власні вектори оператора <А,
що
відповідають власним значенням та /І, (
Я,
# ).
Довести,
що вектор ї
=
ах +
(5
у , а * 0, /? * 0 не є влас-
ним
вектором оператора с4.
§3.
Лінійні оператори в евклідовім просторі
І. Короткі теоретичні відомості
Нехай 13„ - комплексний евклідів простір (унітарний).
Лінійний оператор А називається спряженим до даного лінійно-
го оператора А, якщо
(Ах, у) = (х, А* у)
\/х,уєИ„.
Лінійний оператор <А, що діє в И
п
, називається самоспряженим,
якщо
(А х, у)
=
(х, А у) V х, у є\1„ .
Лінійний оператор
(
1А
, що діє в \]„ , називається унітарним,
якщо
(их,иу)=(х,
у) чх,ує\з„.
Нехай Е„ - дійсний евклідів простір.
Лінійний оператор А, що діє в Е
и
, називається самоспряженим,
якщо
(Ах,у) = (х,Ау) Ух,уєЕ„.
Лінійний оператор А, що діє в Е„, називається ортогональним,
якщо
(Ах, Ау)={х, у)
\/х,уєЕ„.

198
Глава 5. Лінійні оператори
Спряжений оператор має такі властивості:
І) (<А* )* = сА ; 2) (сА®)* =33* А* ; 3) [А + £) * = сА* +
53*
;
4) (агс//)
=а~сА*;
5) (<^*)
= (с//
_1
]
, якщо оператор А невироджений.
Оператори сА та А називаються взаємоспряженими.
Мають місце такі рівносильні твердження:
1. Матриця А - матриця оператора сА в ортонормованому ба-
*
*
зисі <=> матриця А - матриця оператора с/І у тому ж базисі.
2.
Лінійний оператор сА, що діє в И„, - салюспряжений <=> матриця
А оператора <А в ортонормованому базисі - ермітова, тобто А = А .
3.
Лінійний оператор '14, що діє в 1і„ - унітарний <=> матриця і/
*
*
оператора 'ІА в ортонормованому базисі - унітарна, тобто і/ і/ =1/ V = Е.
4.
Лінійний оператор сА , що діє в Е„, - самоспряжений <=> матриця
А оператора сА в ортонормованому базисі - симетрична, тобто А = А .
5. Лінійний оператор
<А
, що діє в Е
и
- ортогональний <=> матри-
ця А оператора <А в ортонормованому базисі - ортогональна, тобто
А А
Т
= = А
т
А = Е .
Теорема (про повноту власних векторів самоспряженого опера-
тора).
Для всякого самоспряженого оператора існує ортогональний ба-
зис,
складений з його власних векторів.
Таким чином, всякий самоспряжений оператор являється опера-
тором простої структури і для всякого самоспряженого оператора існує
ортонормований базис, складений з власних векторів цього оператора.
Самоспряжений оператор має дійсні власні значення.
Симетрична матриця - матриця самоспряженого оператора А в
Е„ - діагоналізовна. Щоб знайти ортогональну матрицю Т, що діагона-
лізує симетричну матрицю А порядку п, треба знайти п ортогональ-
них власних векторів матриці А ; координати / -го (у = 1, п ) нормова-
ного власного вектора матриці А утворюють у -й стовпець матриці Т.
Матриця переходу від одного ортонормованого базису до іншого ортоно-
— 1
т
мованого базису ортогональна Т = Т . Отже,
А'
= Т
Т
А Т = дт
В
(А
1
,А
2
,...,А„),
де всі Х
І
(/ = 1, п) -дійсні числа.

§3,
Лінійні оператори в евклідовім просторі
199
//. Контрольні питання та завдання
1.
Який оператор називається спряженим до оператора
сД
?
Яке його позначення?
2.
Наведіть основні властивості спряженого оператора.
3.
Який оператор називається самоспряженим? Який
вигляд має матриця самоспряженого оператора у ортонор-
мованому базисі?
4.
Якою умовою зв'язані власні вектори самоспряженого
оператора евклідова простору, які відповідають різним
власним значенням?
5.
Чи може комплексне число бути власним значенням
самоспряженого оператора дійсного евклідова простору?
6. Сформулюйте теорему про повноту власних векторів
самоспряженого оператора евклідова простору.
7.
Чи являється симетрична матриця діагоналізовною у
дійсному просторі?
8. Яка матриця називається ортогональною?
9. Як знайти ортогональну матрицю Т, що діагоналізує
симетричну матрицю А ?
10.
Який лінійний оператор називається ортогональним?
11.
Наведіть основні властивості ортогональних
операторів.
12.
Яка необхідна та достатня умова ортогональності
оператора?
13.
Який лінійний оператор називається унітарним?
14.
Яка необхідна та достатня умова унітарності оператора?
///. Приклади розв'язання задач
Приклад 1. Лінійний оператор
сА,
що діє у дійсному евк-
лідовім просторі Е
3
, у базисі Р' = (є,', е'
2
, е'
3
) має матрицю А^.

100
Глава 5. Лінійні оператори
4г=
і
о
2
1 3^
5 -1
7 -З,
Відомо, що
<?,
= ^ + 2е
2
+
е
3
, е
2
=
Є)
+ е
2
+
2е
3
,
<?
3
= е, +
<?
2
і базис Р=(е
1
,е
2
,е
3
) ортонормований. Знайти матрицю
спряженого оператора сЛ* у базисі Р'.
• Позначимо матрицю оператора сЛ у базисі Р через Ар, матрицю
* * *
спряженого оператора <А у базисах р та р' відповідно Ар, Ар .
Зауважимо, що базис р' не є ортонормованим, бо [е'і,е^ •
Випишемо матриці переходу від базису до базису.
1 1 Г
2 1 1
1 2 0
7п'_ьп
- Ті
-і
Р'->р ~
У
Р^Р'
-2 2
1 -1
З -1
0
Л
1
-1
Процес розв'язання задачі такий:
1.
Знайдемо матрицю Ар за формулою
Ар
=
70
4
їТр:
'1 1 Г
р
1
3^
1
'2
2
2 о
;
-3
7
1
Ар =
2 1
1
0
5 -1
1
'2
1
-1
1
=
6
-4
6
,1 2
о,
,2
7
-з,
3 -1
-Іу
1
,6
-5
5,
2.
Знайдемо матрицю Ар за формулою
Г
2
: -З
і
7
6
•4
6
