Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§3.
Лінійні оператори в евклідовім просторі
201
3.
Знайдемо матрицю за формулою
р
2
-2
1 -1
З -1
-і
-З -4 -5
7 6 5
1 1 П
2 1 1
1 2 0
-36
-37
-15
зо зо
14
26
27
9
Приклад 2. Вияснити, чи є ортогональним оператор сА , що
діє в Е
3
, заданий в ортонормованому базисі матрицею А.
А =
72 _72
0
2 2
0
4Ї
72
0
2 2
0
0 0 1
• Оператор є ортогональним тоді і тільки тоді, коли в ортонормовано-
му базисі його матриця ортогональна, тобто виконуються умови:
*=1 I
і
'
1
)•
Перевіримо виконання цих умов.
' її) її
- + -
2 2
^ ЇЇ ЇЇ
Ь
а
\к
а
ік
=-
+ 00 = 0;
1^
а
1к
а
3к =—
0 +
А=1
2
0+01=0;
І^^=^0
+ ^-0 + 0-1 = 0;
*=1
2
^
3
- 'ЯГ ( її
М =
к=\
V
2
,
+ 0 = 1;

202
Глава
5, Лінійні оператори
2>і*
=
к=\
З
4
V
2
У
72"
Ч
2
У
+ 0 = 1;
І4 = о
2
+о
2
+
і
2
= і.
к=\
Отже, оператор А - ортогональний.
Приклад
3. Вияснити, чи являється ортогональним опера-
тор
симетрії відносно площини Оуг у просторі вільних век-
торів
У
3
.
•
Ясно, що оператор симетрії зберігає довжину. Але будь-який опера-
тор,
що зберігає довжину є ортогональним. Отже, даний оператор є ортого-
нальним.
Приклад
4. Знайти ортогональну матрицю Т, що
діаго-
налізує
симетричну матрицю А .
(
3 -
А
=
V
-1
1
•
Відомо, що ортогональна матриця Т, що діагоналізує симетричну мат-
рицю А третього порядку, мас таку побудову, в стовпцях її розташовані коор-
динати трьох ортонормованих власних векторів матриці А .
Тому процес розв'язання задачі складається з таких етапів:
1. Розв'язуємо характеристичне рівняння:
3-Я -1 1
-1 5-Я -1 =0.
1 -1 3-Я
Отримаємо Х[ = 2 , А.2 = 3 , А-з = 6 . Це власні значення матриці А .
2.
Система рівнянь для визначення власних векторів має вигляд
(З-Я)х]-
х
2
+ *з=0;
-Х]+(5-Я)х
2
-
*з
=
0 '•>
X]-
х
2
+(3-Я )хз=0 .

§3.
Лінійні оператори
в
евклідовім просторі
203
Розв'язуємо цю систему послідовно, покладаючи Х\ =2 , Я.
2
= 3,
Я,,
= 6.
Є]
При Х\=2 маємо систему:
X]
—
х
2
+
Х3
= 0 ;
-
X]
+ Зх
2
-
Х3
= 0 ;
х
\
~
Х
2+Х
3
=0
.
З цієї системи отримуємо, що
X)
=(і, 0, -1) - власний вектор;
—т=,
0,
—т=
- нормований власний вектор.
її
л/2;
При Я
2
=
3 маємо систему:
-
х
2
+ Х3 = 0 ;
- X]
+ 2х
2
- хз = 0 ;
х\
- х
2
= 0 .
Звідки знаходимо х-> =(і, 1, 1)-власний вектор; е
2
=( —1= ,—\= ,—1= І
І
л/3 ЇЇ ЇЇ)
нормований власний вектор.
При Я-з = 6 маємо систему:
-Зхі -х
2
+ х
3
= 0 ;
-
Х!-х
2
-
х
3
= 0;
X] -
х
2
- Зх
3
= 0 .
Звідки знаходимо х
3
=
(1,
- 2,1) - власний вектор; є
3
=
нормований власний вектор.
Отже, ортогональна матриця Т має вигляд
^
2_ _1_
л/б'
ЇЇ' ЇЇ
1 1
л/2
л/3
ЇЇ
1 1
л/2
л/3
л/о~
_2_
л/б~
1
1
ЇЇ
ґ
її її
0 її
-її
її
7б

204
Глава 5. Лінійні оператори
3.
Виконуємо перевірку правильності знаходження ортогональної мат-
риці Т - матриці переходу від вихідного базису до базису, складеного з
власних векторів
'Л/з
о -Тзі
А'
= Т
Т
А Г =
1
л/2
л/2 л/2
1 -2 1
Г З -1 1'
-1 5 -1
1 -1 З
1
4~е
{ Із 4г і
л
0 Л/2 -2
-Л/з
Л/2 1
Ґ
2 0 0^|
0 3 0
V
= аіа§ (Я|, Я
2
, Я
3
). (Перевірте!)
0 0 6;
IV. Задачі для практичних занять
У задачах 5.68 - 5.69 лінійний оператор сА у базисі
^' = {е
х
,е
2
, ...,е
п
) має матрицю /4 . Знайти матрицю спряже-
ного оператора <Л* у тому ж базисі Р', якщо вектори
е
х
, е
2
, ...,е
п
задані стовпцями своїх координат в деякому ор-
тонормованому базисі р= (е,,
е
2
,...
,е„).
.
Е
1
=
5
Е*7 —
5.68. А =
.
Е
1
=
5
Е*7 —
7
1
,0,
' 1.
Г і
1
3
1
5.69. /і = 0 5 -1
2 1 1
,2
7
-з,
,2,
,0.
5.70. Оператор А має в деякому ортонормованому базисі
матрицю А . Знайти матрицю спряженого оператора в тому ж
базисі.
{
~\ З 2
Л
а) А =
(2 -г\
б) А =
0 1
З -1

§3.
Лінійні оператори в евклідовім просторі
205
в) А
Го
З
1
-1 2^
4 -5
0 -З,
5.71.
Оператор Л має в деякому ортонормованому базисі
матрицю А . З'ясувати, чи є лінійний оператор <А самоспря-
женим, якщо:
а) А =
2 -1
V
б) А =
V
2 3 0
3 4-1
1 -1 5
в) А
' 1 -1 Г\
-1 2 2
V
1 •2 З
г) А
ґ
0
2
-4
)
2 -Л\
-1 1
1
ь
5.72. За якого значення а оператор, заданий матрицею
А в деякому ортонормованому базисі, є одночасно ортогональ-
ним та самоспряженим?
а) А =
і/л/2"
а
•і/л/2
б) А =
і/л/5 2/л/Т
а і/л/5
5.73.
Лінійний оператор Л в деякому ортонормованому
базисі
е
х
,е
2
,...
,е
п
має матрицю А . Знайти матрицю спряже-
ного оператора Л* в ортонормованому базисі е[,
е
2
,...,
е'
п
,
якщо:
а) А =
б) Л =
ґ-3 О
4 2
1 - 1 - 1 -
Є
2
, Є
2
=-г=Є, +•
л/2
1
л/2 Л ' 72"
-2 '
1 _ 2 .
л/5 л/5
е; =
—г=е
х
+ —^е
2
, е
2
= -т=Є\ —т=е
2
;
2_^
1__
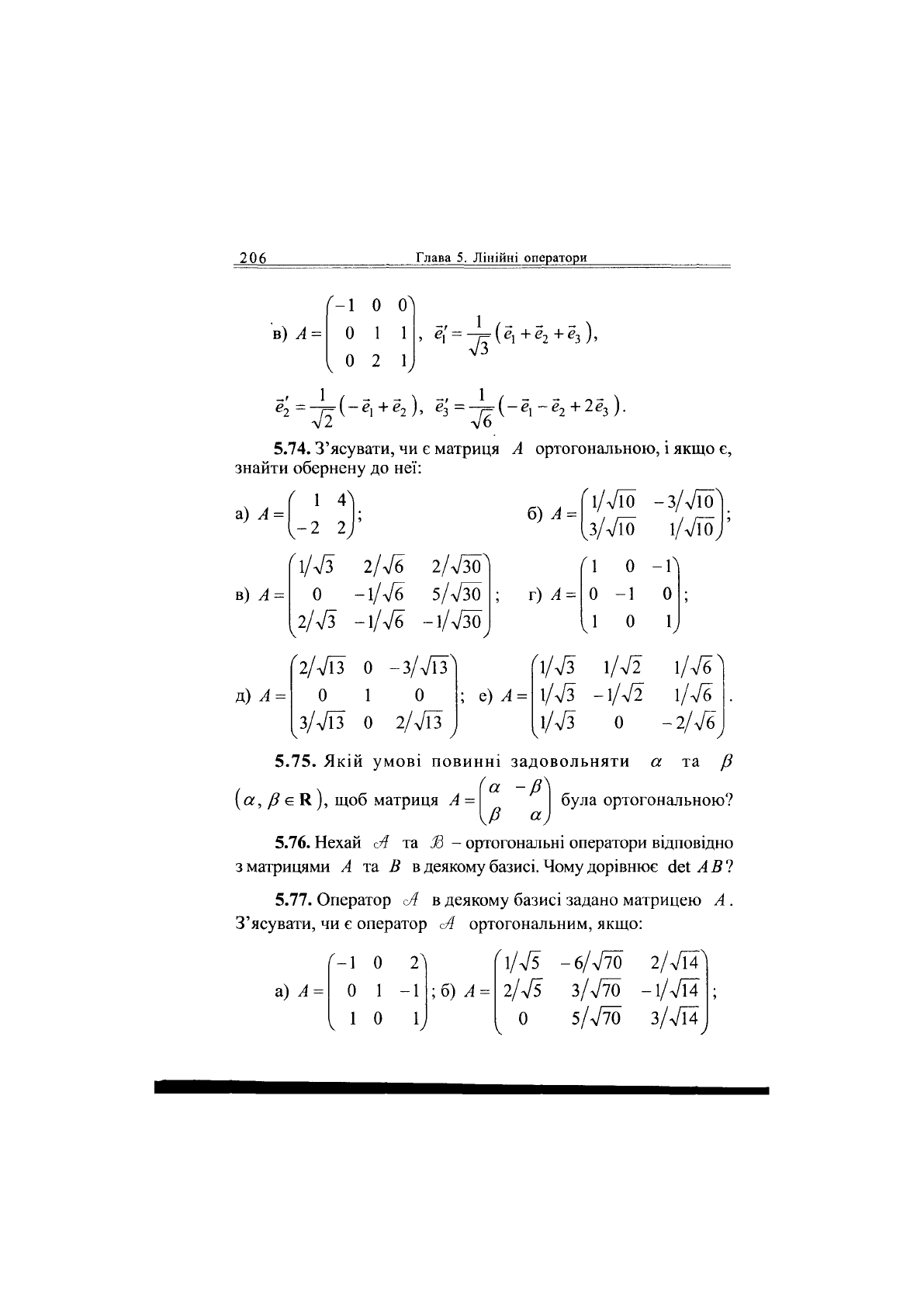
206
Глава
5,
Лінійні оператори
в)
А =
*'
1
і
-10
0
0
1 1
0
2 1
5,
+ е.
е\ = -^={е
х
+е
2
+е
3
),
+
2в
3
).
5.74. З'ясувати,
чи є
матриця
А
ортогональною,
і
якщо
є,
знайти обернену
до неї:
а)
А =
в)
А
1
4
•2
2
і/Уз 2/7б
2/л/зо
0
-1/Уб 5/Узо
2/Уз
—
і/л/б
-і/л/ЗО
б)
А =
г)
/1
і/л/їо -з/Уїо
3/л/Ї0
і/л/То
V
О
о
0
-1
,1
о
-1
Л
о
1
Д)
А
2/УГз
о
-з/Уїз
0
1 о
3/УЇЗ
0
2/л/ЇЗ
;
е) А =
і/л/З
і/л/2
і/л/З -і/лЯ
і/л/з
о
і/л/б
Л
і/7б
-2/л/б
5.75. Якій умові повинні задовольняти
а та /?
(а,
/? є К ), щоб
матриця
/4 =
Р
Р
а
була ортогональною?
5.76. Нехай
оА та 33 -
ортогональні оператори відповідно
з матрицями
А та В в
деякому базисі. Чому дорівнює сієї
АВ1
5.77. Оператор
сА в
деякому базисі задано матрицею
А .
З'ясувати,
чи є
оператор
сА
ортогональним, якщо:
'-10
2"
/70
2/л/Ї4
Л
а)
А =
0
1 -1
;б)А
=
2/л/5
зА
/70
-1/УЇ4
;
1
0
5/л
/70

§3.
Лінійні оператори в евклідовім просторі
207
в) А =
V
2/Уб -і/7з о
л
-1/7б -і/л/З і/л/2
і/л/б і/л/З і/л/2
5.78. Знайти ортогональну матрицю, яка зводить симетрич-
ну матрицю А до діагонального вигляду, та записати діаго-
нальний вигляд цієї матриці, якщо:
а) А =
г) А =
(\
п
,1 1
5
(5 і
1 5 1
1
5,
'3
0
2
1
0 5 0
.2
0
з,
(
б) А =
0 л/5
л/5 4
в) А =
Д) А =
1
-2
0
)
-2
1
0
з
Го і
°1
; е) А =
1 4 2
)
ч°
2
Є) Л:
У задачах 5.79-5.89 виконати вказані доведення.
5.79. Довести такі властивості самоспряженого оператора:
а) власні значення дійсні;
б) власні вектори, що відповідають різним власним зна-
ченням, ортогональні.
5.80. Довести такі властивості унітарного оператора:
а) власні значення за модулем дорівнюють одиниці;
б) для того, щоб лінійний оператор був унітарним, необхід-
но і достатньо, щоб він переводив ортонормований базис у ор-
тонормований базис;
в) унітарний оператор зберігає скалярний добуток векторів;
г) унітарний оператор зберігає довжини векторів.

208
Глава 5. Лінійні оператори
5.81.
Довести, що коли матриця А оператора
А-
симет-
рична в деякому ортонормованому базисі
р
= (е,, е
2
,...,£„ ),
то вона симетрична в будь-якому ортонормованому базисі
$ ={е[,е
2
,...,е
п
).
5.82. Довести, що добуток двох унітарних перетворень є
унітарне перетворення.
5.83.
Довести, що якщо
ЗА
- унітарне перетворення, а А -
самоспряжене, то
Г
ІА~
Х
А
'11
- теж самоспряжене.
5.84. Довести, що якщо один і той же вектор х є власним
вектором для лінійного перетворення А та спряженого пере-
творення А' з власними значеннями Я
{
та Я
2
відповідно,
то Я
{
= Я
г
.
5.85. Довести, що добуток А
33
двох самоспряжених пе-
ретворень А та 33 тоді і тільки тоді буде самоспряженим,
коли матриці цих перетворень А та В переставні.
5.86. Довести, що якщо оператори А та 33 переставні,
то переставні й спряжені оператори А* та 33*.
5.87. Нехай х - власний вектор оператора А , з влас-
ним значенням Я, у - власний вектор оператора А* з влас-
ним значенням /л, причому /и
Ф
Я . Довести, що вектори х
та у ортогональні.
5.88. Нехай х = (х,,
х
2
,
х
3
), А х = (щ
х
х
,
сс
2
х
2
,
а
г
х
3
), де
«і,
а
2
, а
3
- деякі числа. Чи буде оператор А самоспряженим
у дійсному евклідовому просторі; у комплексному
евклідовому просторі?
5.89. Показати, що добуток унітарного оператора на
число а тоді і тільки тоді е унітарним оператором, коли
Іа|
= 1.

ГЛАВА 6. КВАДРАТИЧНІ ФОРМИ
§1.
Теорія квадратичних форм
І. Короткі теоретичні відомості
Означення. Різні форми представлення. Квадратичною формою п
змінних Х[,х
2
,...,х„ називається однорідний многочлен другого сте-
пеня відносно цих змінних:
п п
Ь (Х[, х
2
, ...,х„ ) = £ £ «у
х
і
х
і '
/=1 }=\
де а у - задані числа, коефіцієнти квадратичної форми; ау = ау,, /, / = 1, п .
Матриця А - матриця квадратичної форми.
«11 «12
«21 «22
««! ««2
«1л
«2»
А = А'
Ранг матриці квадратичної форми називається її рангом. Якщо
К§ А = п , то квадратична форма невироджена, у противному випадку
(К§ А < п ) - вироджена.
Матрична форма запису квадратичної форми:
Х
Т
А
X ,
де Х
Т
=
(X]
,х
2
,... ,х
п
); операторна форма запису квадратичної форми:
(сАх, х ) або (х, Ах ), оператор А самосопряжєний, х = (х
х
,х
2
, ••• ,х
п
).
Таким чином: ь(х)= Х
Т
А X
=
(Ах, х)=(х, АХ).
Канонічний вигляд квадратичної форми:
я
і(х) =
У>
г7
х
2
.
/=1
Матриця канонічної квадратичної форми діагональна.
Канонічна квадратична форма називається нормальною, якщо всі
її коефіцієнти а
и
, які не дорівнюють нулю, такі, що
І
а,-,-1
= 1.

210
Глава
6.
Квадратичні форми
Теорема. Будь-яка квадратична форма зводиться до канонічного вигляду.
Зведення до канонічного вигляду.
а) Метод ортогональних перетворень.
Задача зведення квадратичної форми до канонічного вигляду зво-
диться до зведення матриці А квадратичної форми до діагонального
вигляду. Це можливо, враховуючи те, що матриця А - симетрична.
Тому метод ортогональних перетворень полягає в наступному:
1.
Знаходимо ортогональні власні вектори матриці А . Пронор-
мовані власні вектори дають ортонормований базис, в якому матриця
А має діагональний вигляд.
2.
Будуємо матрицю переходу Т з векторів ортонормованого базису
(розташовуємо їх стовпцями). Матриця Т - ортогональна, тобто Т = Т .
3.
Виконуємо перетворення X = ТX', яке зводить квадратичну
форму до канонічного вигляду. Матриця £> одержаної квадратичної
форми діагональна, на головній діагоналі стоять власні числа, тобто
Б = Т
Т
А Г = а
,
іа§(Я
1
, А
2
, ... , Л
п
).
б) Метод Лагранжа.
Метод Лагранжа зведення квадратичної форми до канонічного вигля-
ду полягає у послідовному виділенні у квадратичній формі повних квадратів і
введенні відповідних замін змінних. Цей процес виконується таким чином:
1.
Нехай хоча б один з коефіцієнтів а
н
Ф
0 . У заданій квадра-
тичній формі виділимо члени, що містять Х\ і доповнимо отриманий
вираз до повного квадрату
2
<Ті=ацХ]
+2а\
2
х\Х2+...
+
2а\
п
хіх„ =
2
+ 2 — X, (я,
2
Х
2
+
«13*3
+
• • •
+
а
\п
х
п
) +
X,
«11
+
-у"
(«12*2
+
«13*3
+
• • •
+ а\п
х
п
У
«11
)
-у
=
( і л
= «п
^ ,2
х, + (а
12
х
2
+аізХз+... +
а
]
„х„)
«П
-у:
1
І \2
=
(а,,Х[
+
а
12
х
2
+
а
13
х
3
+... +
а
1п
х„)
-у ,
«11
де у - алгебраїчна сума членів, що не залежать від X].
