Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§1.
Теорія квадратичних форм
221
Т =
1
ЇЇ
2
о
1ЇЇ
2
зїї
5
Це матриця переходу від вихідного базису до канонічного. Вона орто-
гональна. Ортогональним перетворенням, що приводить квадратичну фор-
му до канонічного вигляду, є:
Х
=
Т¥,
х
\
х
2
х
3
)
ЇЇ
2
ЇЇ
- 0
зїї
2
3>/5
5
ЗЇЇ)
Ґ
У1
Л
Уг
Уу
2 1
^
+
ЇЇ
У2
'
1 2
2
зїї
2
зїї
5
зїї
Уз
Уз
Уз
або
х
^-з
п
+
її
У2
'йІ
х
3
ЇЇ
У1
ЗЇЇ
5
ЗЇЇ
уз ;
уз ;
Уз •
(6.2)
4.
Записуємо канонічний вигляд квадратичної форми.
к(Л . Уг. 7з) = "9л
2
+ 9^2
+
9л
2
•
Безпосередня перевірка показує, що
Т
Т
А Г = £> = аіа§(-9, 9, 9).
Крім того, підставивши у вихідну квадратичну форму формули
ортогонального перетворення (6.2) і виконавши всі необхідні алгеб-
раїчні
перетворення, отримаємо канонічну форму Ц{у\, У21 Уз
)•
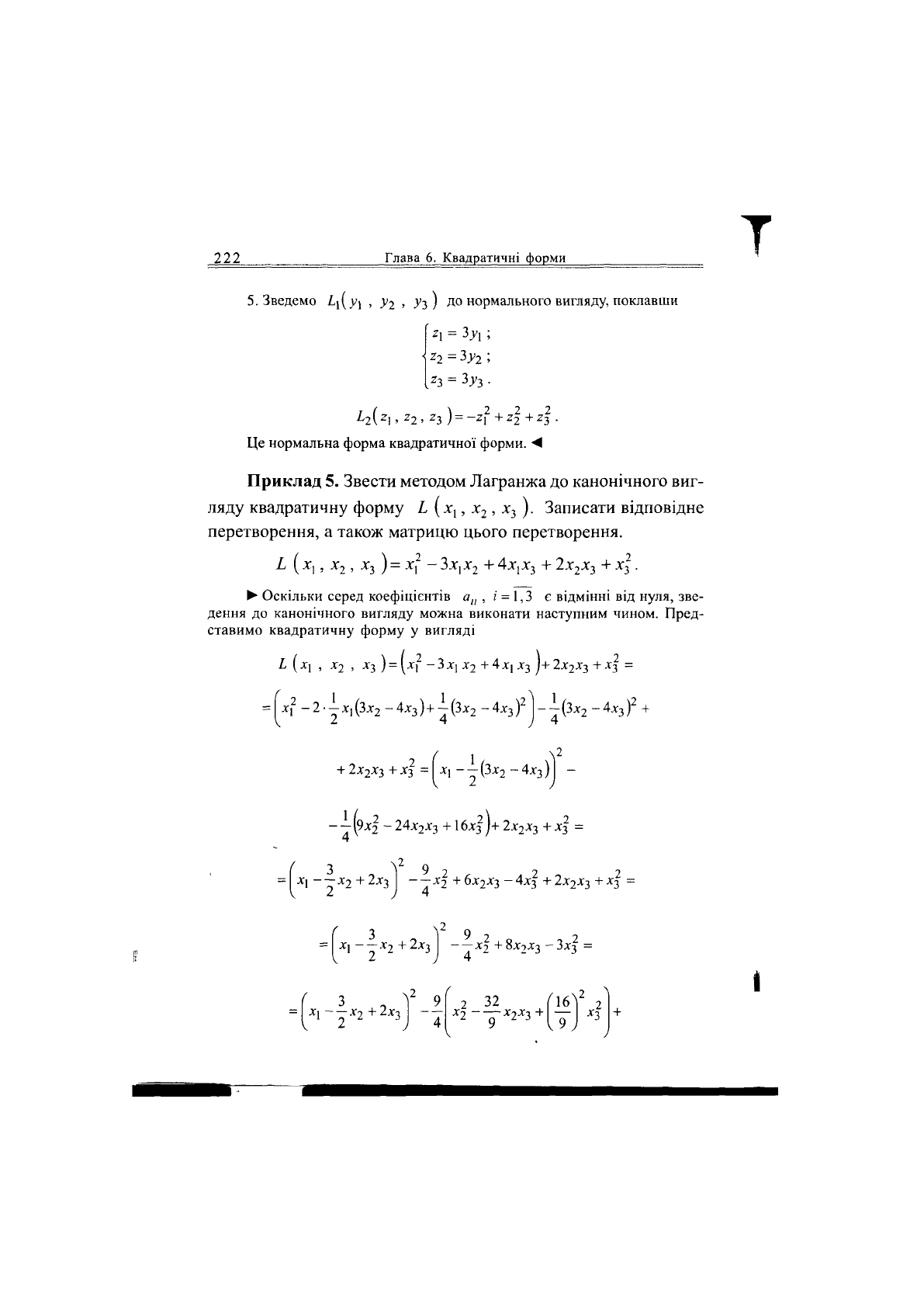
222
Глава 6. Квадратичні форми
5.
Зведемо Іі(уі ,
у і
, Уз) до нормального вигляду, поклавши
2
2 =
3
У2;
2
3
= з^з.
^г(
г
Ь
2
2>
2
3 )=-2і
2
+ 2
2
+г| .
Це нормальна форма квадратичної форми. А
Приклад 5. Звести методом Лагранжа до канонічного виг-
ляду квадратичну форму Ь
(х
{
,
х
2
,
Х3
). Записати відповідне
перетворення, а також матрицю цього перетворення.
1-і
^
Х^
9
Х^
^
Х^
^ —
Х^
3^|Х2
~г*
^"Л^л
-
-^
~\~
^Х^Х-^
~і~
х^
г
з •
• Оскільки серед коефіцієнтів а
и
, / = 1,3 є відмінні від нуля, зве-
дення до канонічного вигляду можна виконати наступним чином. Пред-
ставимо квадратичну форму у вигляді
Ь
(X]
, х
2
>
х
3
) = (х
2
-
З
X]
х
2
+ 4 хі х
3
)+ 2х
2
х
3
+ х
2
=
= (*? -
2 •
|
х,
(Зх
2
- 4х
3
) + ~ (3*2 - 4х
3
)
2
1 - і (Зх
2
- 4х
3
)
2
+
+ 2х
2
х
3
+х
3
=| х,--(Зх
2
-4х
3
)
-
—
(9х
2
-24х
2
х
3
+16х
2
)+2х
2
х
3
+ х
2
=
З V 9
2
,
2
X]
-
~*2
+2хз І ~~
х
2 +6х
2
х
3
-4х
3
+2х
2
х
3
+х
3
=
З 1 9
2
2
X]
х
2
+ 2х
3
х
2
+ 8х
2
х
3
- Зх
3
*1
9
/
2
32
16^
2 "і
2
4
х
2
-
1
- — х
2
х
3
+
,9,
х
3
/

§1.
Теорія квадратичних форм
223
+
—
-^^-х
2
- Зх? =|
Хі
-
—
х? + 2х
3
4
81
3
3
V 2
1 3
Покладемо
16
4І
Х2
"Т
ХЗ
37
2
+
Х
3
.
9
3
У\ =хі - 1,5x2 + 2*з ;
16
Уг
=
х
2 ~
9
х
з;
Уз=
х
з-
Тоді і (Х[, х
2
, х
3
) прийме вигляд Ц (>>і, у
2
, Уз ).
(6.3)
9
2 37 2
що представляє канонічний вигляд вихідної квадратичної форми.
Розв'яжемо (6.3) ВІДНОСНО X] , х
2
, х
3
. V
ЗГ 16 "і „
х
\
= у\ +
2
\У2 +
9
уз \~
2
уз ;
іб
*2
=У2+—уз ;
*з =л.
або
З 2
*1
=Л + ^У2
+
^Уі
16
*2
=У2+у>'3
;
х
з
=Уз •
(6.4)
Можна перевірити, що підставивши (6.4) в задану квадратичну
форму, отримаємо її канонічний вигляд Ц{у\, У2> Уз)- Таким чином,
(6.4)
є те перетворення, що зводить квадратичну форму до канонічного
вигляду. Матриця цього перетворення
\
3
-
2
0 1
0 0
з
16
9
1

224
Глава 6. Квадратичні форми
Перехід до діагональної матриці О канонічної квадратичної форми
виконується так
т ( 9 37 ^
V
4' 9 )
(Перевірте!) М
Приклад
6. Звести квадратичну форму Ь (х
і
, х
2
, х
3
) до
канонічного
вигляду методом Лагранжа. Виписати
відповідне
перетворення, а також його матрицю.
•
У квадратичній формі відсутній квадрат змінних, тобто всі
а
й
= 0 . Тому виконуємо невироджене лінійне перетворення.
х
і
=У\ -У2'>
•
х
2 =
У\ +
Уі; - (
6
-
5
)
.
х
г =
Уг
•
В результаті отримаємо квадратичну форму, в якій коефіцієнт при
у
2
не дорівнює нулю.
к(у\>У2>
Уг )
=
2
(У\ ~Уг
){у\+Уг )~
6
(УІ
~Уг Ьг+ІІУі+Уг )уг =
= 2уї - 2уі -
4у\Уз
+
%УгУг
=
=
І(У\ -
2у\Уг
+ Уг
)-
Ьг - -
ЬгУг
+ Ьг )+
%Уг
=
=
2(У\-Уг )
2
-2{у
2
-Ьг Г+&УІ-
Покладемо
2
і
= Уі - Уг;
•
г
2
= у
2
- 2у
3
; (6.6)
.
2
з = Уг •
Тоді квадратична форма прийме вигляд:
Ь
2
(г\,
г
2
, г
3
)=2г
2
-2г
2
+62],
що представляє канонічний вигляд вихідної квадратичної форми.

§1.
Теорія квадратичних форм
225
Розв'яжемо (6.6) відносно у\, Уг, Уз
у\
=
2
і +
2
з;
у
2
= 2
2
+ 2г
5
;
УЗ
=
2
3 •
Підставимо (6.7) в (6.5). Отримаємо
х
і =
2
і ~
2
2 -
2
з;
х
2
—
2
1 +
2
2 + ;
*3 =
2
3 •
(6.7)
(6.8)
Формули (6.8) представляють собою перетворення, яке треба за-
стосувати до квадратичної форми Ь (х\, х
2
, *з ), щоб отримати кано-
нічну форму І
2
(
2
1»
2
2
>
2
з )
•
Можна безпосередньо в цьому впевнитись, підставивши (6.8) в
і(
*1,
х
2
, х
3
). (Перевірте!)
Матриця перетворення (6.8)
' 1 -1 -1
Л
Т =
Перехід від матриці А квадратичної форми до матриці й ка-
нонічної квадратичної форми виконується так
Г
1
Л7
,
= £ = сна§(2
>
-2, 6).
(Перевірте!)
Зауважимо, що матриця Т перетворення (6.8) може бути отри-
мана з урахуванням матриць перетворень (6.5) та (6.7).
Дійсно, матриця перетворення (6.5)
А,
=
-1 0^
1 0
0 1

226
Глава 6. Квадратичні форми
Матриця перетворення (6.7)
'\
0 П
А
2
=
0 1 2
0 0 1
Тоді матриця перетворення (6.8) отримується так:
( 1 -1
°]
(\
0
(
1
-і
-П
Т = А
1
А
2
=
1 1
0 0
1 2 1 1 3
0
1
,0
0
\ \
0
о
1
що співпадає з отриманим раніше. -4
Приклад
7. Звести до канонічного вигляду методом
Якобі
квадратичну форму
•
Матриця даної квадратичної форми має вигляд:
( 2 -2 \
л
•2 З -1
1 -1
її головні кутові мінори А] = 2 , Д
2
= 2, Д
3
=
1
відмінні від нуля.
Канонічний вигляд квадратичної форми
де
р,=А,;
Р
2
=4
2
-;
Рз =
Лз
л
2
'
"1
Тому р,=2; 02=1 = 1; Рз=|-
Отже, канонічна квадратична форма має вигляд:
к(Уі>У2>
УЗ ) =
2
Уі + Я + •
§1.
Теорія квадратичних форм
227
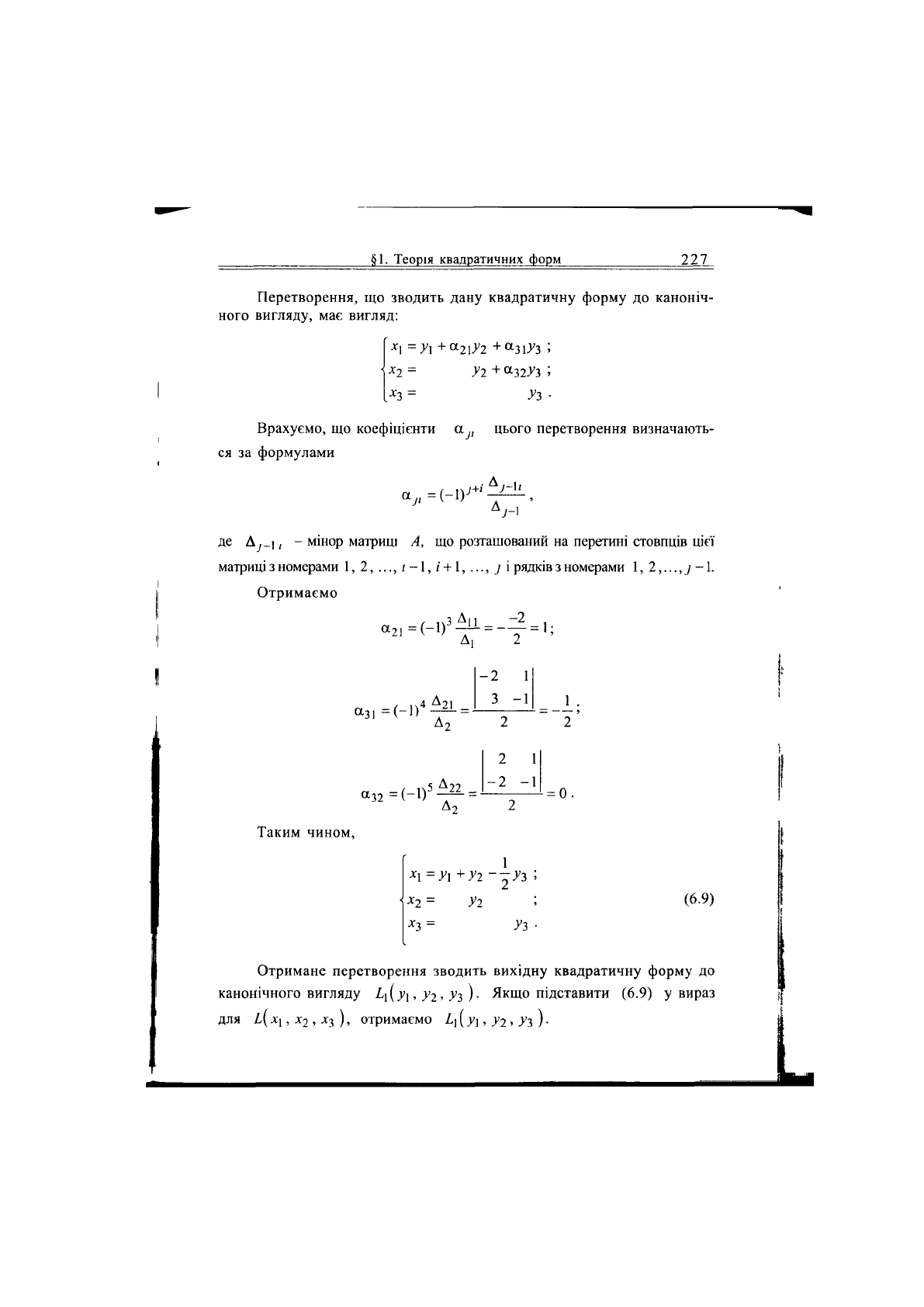
Перетворення, що зводить дану квадратичну форму до каноніч-
ного вигляду, має вигляд:
Врахуємо, що коефіцієнти а
]{
цього перетворення визначають-
ся за формулами
де Д^_], - мінор матриці А, що розташований на перетині стовпців цієї
матриці з номерами 1, 2, ..., і
-1,
і +1, ..., у і рядків з номерами 1,
2,...,
у
-1.
Отримаємо
х, =у
х
+ а
21
у
2
+СІ31У3
;
х
2
= у
2
+ а
32
у
2
;
х
з = Уз •
-2 1
З -
1
1 .
а
3
і =(-!)•
2 2
2
-2 -
а
32
= 0.
2
Таким чином,
(6.9)
х
3
=
Уз •
Отримане перетворення зводить вихідну квадратичну форму до
канонічного вигляду Ц{у\,
У2>
Уз)- Якщо підставити (6.9) у вираз
для і(
Х[,
х
2
,
Х3
), отримаємо
Ь\
(у
х
, у
2
, у
3
).

228
Глава 6. Квадратичні форми
Матриця перетворення (6.9)
1 1 --
0 1
0 0
Діагональна матриця Б канонічної квадратичної форми отри-
мується так:
Т
1
АТ
=
£>
=
оїа^2,1,1
(Перевірте!)
Приклад 8. Дослідити на знаковизначеність квадратич-
ну форму
./>
(, х
2
, х
3
)
—
5Х|
-ь
Зх
2
~ь
Зх
3
4Х|Х
2
"Ь
2х^х
3
4х
2
х
3
.
• Матриця квадратичної форми має вигляд
А =
5 -2
-2 З
1 -2
її головні кутові мінори:
5 -2
А!=5>0, Д
2
-2
11 > 0, Д
3
=оеіЛ = 18 > 0 .
Отже, згідно з критерієм Сильвестра, квадратична форма додат-
но визначена.-^
IV.
Задачі
для
практичних занять
6.1.
Записати матриці кожної із заданих квадратичних форм.
а) ь{ х
1
, х
2
) = 2х
2
- х\ +
4Х)Х
2
;
б) ь(х
х
, х
2
) = х
2
+ Зхі -
х
\
х
2 '

§1.
Теорія квадратичних форм 229
в) Ь(х
и
х
2
)
=
х
2
-2х
2
; г) Ь(х
{
, х
2
)-Зх
х
х
2
;
х,, х
2
, х
3
) = X
і
- 2х
2
+
х
2
- 6х,х
3
;
с)
х^,
х^,
х-^
)
—
"Г~
х^
2x2X3
9
є) 5 ' ^3 )
—
ЗХ|
Х^2 "т" -5^з
'
Х| , Д*2 ^ Х3 ^ — *^*1"^"2 '
з)
Х|
?
^2
?
Х^
?
Х^ ^
—
^2
^-^3 ^-^4 ^^1^2
2X3X4
;
(
\ 2^2 2
Х|, х^
5
Х3, х^ )
—
ЗХ|
~і"
х^
"і~ 2х^
Х|Х^ ,
6.2. Знайти ранг кожної із заданих квадратичних форм.
а) Ь{ х,, х
2
) = х
2
+ 4х
2
+ 4х,х
2
;
б) Ь( х
х
, х
2
) = х
2
+ 2х
2
- 6х
(
х
2
;
в)
Х|
, х
2
, х
3
) ~ х, 2х
2
Зх
3
-ь
4х,х
2
-і-
6х,х
3
-ь
2х
2
х
3
;
г)
^( Х|,
х
2
, х
3
^
—
2хі Зх
2
Зх
3
2х
х
х
2
-ь
2х,х
3
§х
2
х
3
,
д)
УІ/( Х|,
х
2
, х
3
, Хд )
—
2Х| х
2
4- Зх
3
Ч"
х^ .
6.3.
Записати квадратичну форму Ь(х
]
,х
2
,...,х
г!
) у мат-
ричному вигляді, якщо:
а) /,(х,, х
2
) = Зх,
2
+ 2х
2
- 6х,х
2
;
б) Ь(х
х
, х
2
)
=
х\
+
Зх,х
2
; в) і( х,, х
2
) = 2х
2
- х
2
;
г) x^
9
Х2 Х3) — х^ -^-^2 4X2X3 \
д) X],
Х2 5
Х3 ^
—-
5Х|
~і~
2x^Xз
-^^з*
І^і^
Х|
,
Х2
9
Х3 ^
—
Х|Х2
"І"
Зх^х^ 2X2X3
.

230
Глава
6.
Квадратичні форми
6.4.
Записати квадратичну форму
ь(х
]
,х
2
,...,х
п
) у виг-
п
п
ляді
£ X
а
г
]
х
,
х
1
за
заданою матрицею
А :
1
=
1
у = 1
1
_2
1
Го
б)
Л =
V
2
б)
Л =
.1
/
2 -2 СУ
гз
0
2
1
-1
;
г) л =
0
-2 1
V
0 -1
І2
1
1
Го
5
°1
д)
Л =
5
-3
0
;
е) А
,о
0
о,
ґ
-\
3 0 1
3
0 4 0
0
4 2 5
,10
5 0
6.5.
Знайти ортогональне перетворення,
яке
зводить
до
канонічного вигляду квадратичну форму
Ь(х
{
,
х
2
,...,
х„)
та записати відповідний канонічний вигляд квадратичної
форми, якщо:
а)
і(х,,
^
—
2Х|
н~
2x2
2Х|Х2
^
б)
і(х
и
Л^2
)
—
+
2х^
+
2д/б
Х]^2
^
в)
і(х,,
•^2
)
—
2Х|^2
;
г)
і(х,,
^2
9
Х3
)
=
ЗХ|
~г"
ЗХ2
2Х|Х2
~Ь
4Х|Х^
~І~
4X2X3
?
д)
Х2
у
х^)
—
7Х|
Ч"
7x2
^"^3 2x^2
н~ 2Х|Х^ н~
2x2X3,
е)
і(х,,
Х2
у
Х3)
—
2Х|Х2
"і~
2Х|Хз
у
є)
і(х,,
Х2
)
Х3
^ —
Х|
*т*
Х2
*4"
Х3
™~
2x^X2
~~*
2Х|Хз 2X2X3
•
