Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§2.
Використання теорії квадратичних форм
241
Приклад
2. Звести до канонічного вигляду задане рівнян-
ня
поверхні другого порядку та побудувати її.
Зх
2
+ 5у
2
+ Зг
2
- 2ху + 2хг - 2уг -12х -10 = 0 (6.19)
•
Рівняння (6.19) задане в системі координат ((9; і, і, к
).
Матриця квадратичної форми, що присутня в (6.19), має вигляд:
3-1 Г
-1
5 -1
1
-1 7>
/
Виконуємо зведення рівняння до канонічного вигляду таким чином:
1.
Складаємо характеристичне рівняння
3-Х. -1 1
-1
5-А. -1 =0.
1
-1 3-Х,
Звідки
(3-А.)(А.
2
-8А. + 12)=0.
Отримуємо власні значення
А,
=
2 , Х2
—
3 , А-з = 6 .
2.
Знаходимо власні вектори, використовуючи систему
(3-А.)х,-
х
2
+
*з=0;
-х,+(5-А)х2
-
Хз=0;
х
\~
х
2 +(3 + А.)х
3
=0 .
У цій системі послідовно покладаємо А] = 2 , А
2
= 3 , А3 = 6 .
а) А, = 2 ;
х
\
-
х
2
+ х
3
=
0;
~
Х
1
+ 3х
2
-*з
=
0;
х
і
-
х
2
+ Хз
=
0.
(
1
-1
г
'\
-і г
А-2Е
=
-1
3
-1
~
0 2
0
,
1
-1
,0
0
0,

242
Глава 6, Квадратичні форми
г = К£{[А-2Е)=2; п-г =
1
=> 3 один лінійно незалежний влас-
ний вектор, що відповідає Х
х
.
Скорочена система для визначення власного вектора:
х
\ ~
х
2
+
х
3
=
о;
2х
2
= 0 ,
*3 =
-
х
\ +
х
г;
х
\ =
і;
х
2
= 0;
=> •
х
2
=
0;
х
х
=
1,
/з =
-і.
х\
=(і, 0, - і) - власний вектор, і?) =
ний власний вектор,
б) Х
2
= 3
;
- нормова-
- х
2
+ х
3
= 0 ;
- X) + 2*2
_
*з
=
о;
X] -*2
=
0
•
' 0 -1
г
' 0
-1
0
(
0 -1
А
-1 2 -1 -1 2 -1 ~ -1 1
0
-1
о,
V
0
1
-0
0 0
о,
г = К§(Л-3£)=2;л-г =
1
=> 3 один лінійно незалежний влас-
ний вектор, що відповідає Х
2
.
Скорочена система для визначення власного вектора:
- х
2
+ х
3
= 0 ;
-Х| +х
2
= 0 ,
х
2
= х
3
;
х
\~
х
2 >
х
3
=
1,
X] =1;
х
2
=1;
х
3
= 1.
х
2
=(і, 1, і) - власний вектор, е
2
,7з'
>/з' л/з
- нормований
власний вектор,
в) Ц = 6;
• Зхі - х
2
+ х
3
= 0;
- X] - х
2
- х
3
= 0;
х\
- х
2
—
3х
3
= 0.

§2.
Використання теорії квадратичних форм
243
ґ-з
-і
г
і
0
2
4^
Го
1
2*
А-6Е
=
-і -і
-1
~
-і
-1 -1
~
і
1 1
,
і
-і
-V ,
0
-2
0
о,
г = Кц(А-6Е)=2; п-г = \ => 3 один лінійно незалежний влас-
ний вектор.
Скорочена система для визначення власного вектора:
[ х
2
+ 2*з = 0 ;
І
х, + х
2
+ *з = 0 ,
х\~
- х
2
-х
г
;
х
2
=-
2х
г
;
*з
=
1
>
х\=
1;
х
2
=
-
2
;
х
3
= 1.
х
3
= (і, -2, і) - власний вектор, е
3
=
^
2_ _[_
л/б
'
л/б'л/б
нормова-
ний власний вектор.
Вектори ?|, е
2
, е$ - ортогональні та нормовані. ?^ )=<5у .
Маємо нову систему координат (О; е
х
, е
2
, е
3
), яка отримується з
попередньої поворотом на відповідний кут.
3.
Записуємо матрицю переходу від базису і , у , к до базису
е\,е
2
,е
г
.
1
УІ2
л/з
0
1
1
л/о"
_^2_
л/3
л/б
1 1
л/2
л/3
1
Матриця Г - ортогональна.
сієї Т = 1, тобто буде збережена взаємна орієнтація осей при пово-
роті системи координат.
4.
Використовуємо лінійне перетворення
X
= ТХ'.

244
Глава 6. Квадратичні форми
Х =
{ 1 і
\
ЇЇ
ЇЇ
її
0
і
2
У
—
0
ЇЇ її
1 1
1
, ЇЇ
ЇЇ
ЇЇ
х
\
У\
1
2
1
тобто
її
Хі+
її
У\+-
1
ЇЇ'
1 2
(6.20)
Підставивши формули перетворення (6.20) в задане рівняння по-
верхні (6.19), після перетворень отримаємо, що матриця А квадра-
тичної форми прийме діагональний вигляд А
—>
Б = ш'а§ (Л
х
, Л
2
, Л
3
) і
група старших членів представиться так:
Зх
2
+
5у
2
+
З2
2
- 2ху + 2x2 - 2уг
= |
X = 7Х'
|
= 2л,
2
+ Зу
2
+ б7
2
.
(Перевірте безпосередньою підстановкою).
Група лінійних членів прийме вигляд:
-ш
=
|^гг|
=
-|,-|
Л
-|
гі
.
Вільний член не змінюється.
Таким чином, рівняння поверхні у змінних *
(
, у\,
2\
приймає вигляд:
.1,2,2 12 12 12
2*і +3у(
+
6г( ~~^
х
і ~П^
У
^ ~7б
21
~
=
'
(6.21)
5.
Виділяємо повні квадрати відносно змінних х
х
, у
х
, г
х
в рів-
нянні (6.21).
ЇЇ'
х
х
+3
Уі
ЇЇ'
Уі +
6
2,2
~Ж
Х
Н
0
= 0
'

§2.
Використання теорії квадратичних форм
245
2,3 9
\ І
+ 3
Тз""
з
=
10
+ 9 + 4 + 1,
2 / ч2
+ 6
2,1 1
+ 3
*1
_2_
л/з~
+ 6
' 2
^
\2
Ге.
=
24,
\2
л/б
12
Покладемо
*2
8
З
22
=
21
"X
І-
= І.
(6.22)
О,
Це відповідає паралельному переносу початку координат у точку
З _2_ _іЛ
Іл/г'
ліз' л/б)'
Отримаємо рівняння
2 2 2
12 8 4
Це канонічне рівняння еліпсоїда.
Воно записане у системі координат (0\; е\, е
2
, е$).
(6.23)
6. З формул паралельного переносу (6.22) знайдемо вираз х
х
, у\,
2]
через *
2
, >^2 , ^2 та підставимо у формули перетворення (6.20).
Отримаємо результуюче перетворення координат (6.24).
Х]=Х2+
42
;
Уі=У2+
7з
;
2І =
22+
7Г
246
Глава 6. Квадратичні форми
1 ( З "і 1 ( 2 ) 1 ( 1
2 = -
1
ЇЇ
х
2
+-
1
л/з"
1
2) 2 '
2
2
+
і
_і_
?2
"І,
1
або
1117
*
=
;Г
2+
7Г
2+
;/Г
2+
з
;
1 2 1
тг
2
-;Г
2+
з-
;
1112
(6.24)
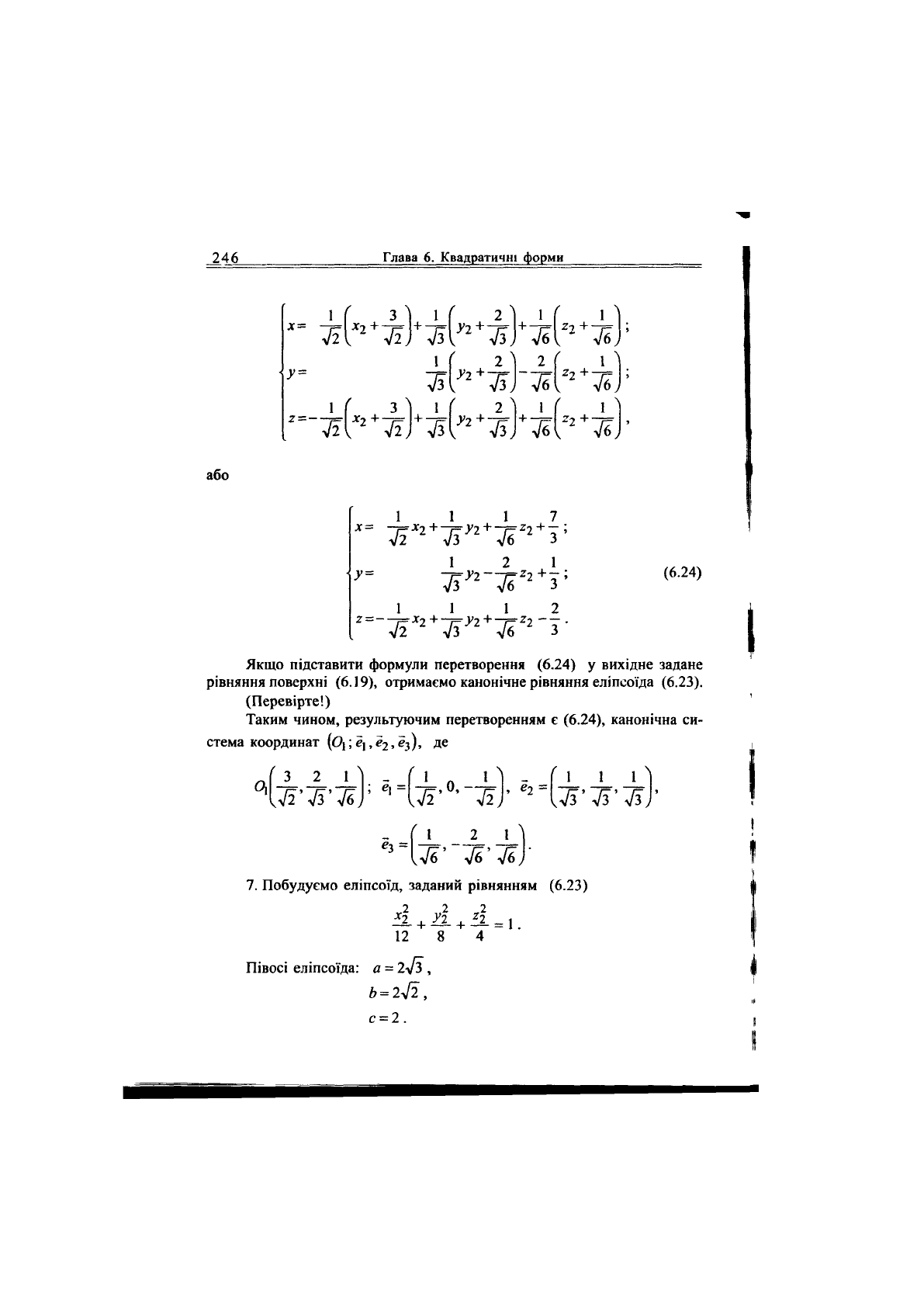
Якщо підставити формули перетворення (6.24) у вихідне задане
рівняння поверхні (6.19), отримаємо канонічне рівняння еліпсоїда (6.23).
(Перевірте!)
Таким чином, результуючим перетворенням є (6.24), канонічна си-
стема координат (Оі,Єі,е
2
,е
3
), де
Ох
Г_3_
_2_ 1
>/2'л/з'7б
|;
Єі
1
,о.
1
1 1 1
_1 2 1_
7. Побудуємо еліпсоїд, заданий рівнянням (6.23)
2
2 2
12 8 4
Півосі еліпсоїда: а - 2л/з,
ь=г4г,
с = 2.

Рис.
6.2 -«
IV. Задачі для практичних занять
У задачах 6.21 - 6.26 звести до канонічного вигляду зада-
не рівняння кривої другого порядку та побудувати її. Виписати
канонічну систему координат.
6.21.
9х
2
- 4ху
+
6у
2
+
\6х - 8> - 2 = 0 .
6.22. х
2
-2ху
+
у
2
-\0х-6у
+
25 = 0.
6.23. 5х
2
+ 12ху - 22х -12>> -19 = 0 .
6.24. 4х
2
-4ху + /-6х + 3.у-4 = 0.
6.25. 2х
2
+
4ху
+
5у
2
-6х-%у -1 = 0.
6.26. х
2
-4х>' + 4г>
2
-4х-3>>-7=-0.
У задачах 6.27 - 6.34 звести до канонічного вигляду зада-
не рівняння поверхні другого порядку та побудувати її. Виписа-
ти канонічну систему координат.

248
Глава
6. Квадратичні форми
6.27. їх
2
+
6у
2
+
Ьг
г
- 4ху - 4уг - 6х - 24у +18г +
ЗО
= 0.
6.28.
2х
2
~7у
2
-4г
2
+4ху+20у2-Іб2Х+60х-\2у+\22
-90=0.
6.29. 2х
2
+
2у
2
- 5г
2
+
2ху - 2х - 4у - 4г +
2
= 0
•
6.30. 2х
2
+2у
2
+3г
2
+Лху
+
2уг
+
2гх-4х
+
6у-2г
+
3
=
0.
6.31.
4х
2
+у
2
+42
2
-4ху+4уг-82х-28х+2у+16г+45=0.
6.32. 2х
2
+5у
2
+2г
2
-2ху-4х2 + 2у2
+
2х-\0у-22-\ =
0.
6.33.
х
2
+
5у
2
+
г
2
+
2ху
+
2уг + бгх - 2х
+
6у + 2г = 0
•
6.34.
х
2
-2/+2
2
+4х>'
+ 4>2-102х + 2д:-і-4>'-102-1 = 0.

ГЛАВА
7.
ГРАНИЦІ
ТА
НЕПЕРЕРВНІСТЬ ФУНКЦІЙ
§1.
Гоаниці послідовностей
та
функцій
І.
Короткі теоретичні відомості
Послідовність. Границя послідовності
Основні поняття. Якщо кожному натуральному числу
п є N
ставить-
ся
у
відповідність число
х
п
, то
множина чисел
.Г|,
х
2
,...,х„,...
називається
числовою послідовністю
або
просто послідовністю.
Скорочено послідовність позначається символом
{х„} .
Числа
х
п
,
п є N , називаються
членами послідовності,
х
п
= /(«) -
загальний член
послідовності.
Число
а
називається
границею числової послідовності
{х
п
},
якщо
для довільного
є > 0
існує такий номер
УУ(Є)
, що для
всіх
п > ^(є),
вико-
нується нерівність
|х„-а\<Е.
Символічно
це
записується так:
Ііт
х
п
= а або х
п
—>
а при п -»
оо
.
И-КЮ
Послідовність
{х„}, яка має
границю
а ,
називається
збіжною.
По-
слідовність, яка
не є
збіжною, називається
розбіжною.
Враховуючи,
що
нерівність |х„-а|<є рівносильна нерівності
а-г<х
п
<а + е, яка
означає,
що х
п
належить г-околу точки
а
0(а,е),
маємо
геометричний зміст границі
а
послідовності
{х„}: для
будь-якого
є
> 0 всі х„ є 0(а,
є), починаючи
з
деякого номера
п >
/У(є).
Послідовність
{*„}
називається
обмеженою,
якщо ЗМ>0 таке,
що
Уи
\х
п
\<М
.
Послідовність
{х„},
називається
зростаючою (спадною),
якщо
*
И+
1
>
х
п (
х
п+1 <
х
п) Д
ЛЯ
ВСІХ
П
•
Послідовність
{х„},
називається
неспадною (незростаючою),
якщо
х
п
+
\
*
х
п
(Х
и+
і
<
Х„
)
ДЛЯ
ВСІХ
И
.

250
Глава 7. Границі та неперервність функцій
Зростаючі та спадні послідовності називаються строго монотонними.
Неопадні та незростаючі послідовності називаються.монотонними.
Будь-яка обмежена та монотонна послідовність збіжна.
Критерій Коті збіжності послідовності. Для того, щоб послідовність
{х
п
} була збіжна, необхідно та достатньо, щоб для довільного £ > 0 існував
такий номер И{г), що | х
т
- х„
\
< с для всіх т,п > Л^(є).
( 1V
Число е. Ііт
1
н— = е.
е - ірраціональне число, 2 < е < 3, е = 2,71828182...
Якщо за основу логарифма взято число е, його називають натураль-
ним логарифмом і позначають
1п
х.
Послідовність {а„} називається нескінченно малою, якщо
Ііт а„ = 0.
Нескінченно малі послідовності {а„} та {р„} називаються еквіва-
а
лентними, якщо Ііт —- = 1. Пишуть а„ ~ р„.
Мають місце такі властивості нескінченно малих послідовностей.
1°.
Алгебраїчна сума скінченного числа нескінченно малих послідов-
ностей є нескінченно мала послідовність.
2°.
Добуток нескінченно малої послідовності на обмежену є нескінчен-
но малою послідовністю.
Послідовність {х
П
\ називається нескінченно великою, якщо для
довільного числа М > 0 знайдеться такий номер И{М), що для всіх
и>ЛГ(М)
\
х„\>М.
Символічно це записується так: Ііт х„ =
оо
.
7Ї—ЮО
Серед нескінченно великих послідовностей виділяють такі:
Ііт х„ = +<», Ііт х„ = -оо.
Нескінченно великі послідовності {х„} та {у„} називаються
х
еквівалентними, якщо Ііт — = 1. Пишуть х
п
~ у„.
п->*.у
п
