Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§
1.
Границі послідовностей та функцій
261
Для розкриття заданої невизначеності типу | — | виносимо в чисель-
нику та знаменнику вищий степінь л . Після скорочення та врахування того,
що Ііт
—
= Ііт -Хг = 0 , а також властивостей арифметичних дій над збіжни-
л—»СО
П Л—>00 у}
ми послідовностями, маємо:
Зл +4л +
1
С
оо
Ііт
л->
С0
2и''
-5л + 7
Ііт
-
4 1
п
1
3 + - +
п п
оо
І
я->°О
2[
•>
^ 7
л
І
2-- + —
Л п
Ііт
/1—>00
л Л
Розв'язання буде простішим, якщо врахувати, що
а
0
п
к
+а
х
п
к
~
х
+... + а
п
~ а
0
п
к
при л
—>
оо
,
бо Ііт
Нт
Н—>0О
-
+ ... +
-
а
п
л
а
п
л
= 1.
О"
у
Тоді
Ііт
Зл +4л +
1
2л
2
-5л + 7
Зл
2
+4л +
1
~3л
2
2л
2
-5л+ 7-2л
2
Зл
= Нт —-
"-
>0
° 2 л
б) Нт
+ 4л
«^лУл
3
-Зл
2
Нт
00
І
п—>АО
ЗІя
3
[і--
=
Ііт
-
л Л +
-
л зі
=^=1
Інакше
Нт
4л
-Зл^
2
, /і 2
я + 4и ~ п
л
3
-Зл
2
~л
3
Л
—>
со
Нт - = 1.

262 Глава 7. Границі та неперервність функцій
Скористаємось тим, що
л!=1-2-3-...л; п\=(п-\)\п; (л + 2)!= л!(л + 1)(л + 2).
Тоді маємо
(и + 2)!-л!
оо і ,. л!(л + 1)(л + 2)-л!
Ііт
Ііт
«->«>п
г
{п\+(п~\)\) І
оо
) «->°° л^((л-1)!л + (л-1)!)
= Ііт
л!((я + 1)(и + 2)-і)_ л(л
2
+3л + 1) _
"-*
00
л (л-1)!(я + 1)
л
2
(л + 1)
л
2
+3л +1 ~ л
2
п +1 ~ л
Л —>• 00
= Ііт —
г
= 1.
г) Ііт
1
+ 2 + ... + «
л/4л
4
-л
2
+1
оо
Маємо невизначеність типу | — ^. У чисельнику маємо суму л членів
арифметичної прогресії, сума 5,, якої обчислюється за формулою
а, +а
—
п
. Крім того, в знаменнику скористаємось тим, що
4л
4
- л
2
+
1
~ 4л
4
при л
—» оо
. Отже,
1
+ л
1+2 +
..,
+
п І оо І 2 і- п~
+
п
Ііт = і —
!>
= Ііт
—^-х—
= Ііт
•
"-""ЇЇп
4
-л
2
+1 ^
00
"~*"
=0
2и
2
"-»
00
4л
2 , 2
л + л ~ л
Л —» 00
Ііт
л"
_ 1
4л
2
4
д) Ііт -^-^—
=
і
— 1
= Ііт —^— = 5.
п
-*оо 3"
—
2 І
00
і "
_>а:)
| 2
Тут чисельник і знаменник поділено на 3
я
.

§
1.
Границі послідовностей та функцій
263
Приклад 3. Знайти границю Ііт(л/л
2
+ п - п).
• Тут маємо невизначеність типу
{со
-
со}.
Для її розкриття множимо
чисельник і знаменник на вираз, спряжений до чисельника, і користуємось
формулою: (а - Ь)(а + Ь) = а
2
-Ь
1
.
,. , Г~2 ч < >
(\п
2
+п-п)(уіп
2
+п+п)
Ііт (\п +п -п) = { оо-оо }= Ііт ==^= =
П—»СО
П—>О0
А 2 ,
\П
+П +П
2
1
Ііт ——
=
Ііт
'л/«
2
+п +п
"^ліп
2
+п +п
2
2
п
+ п ~ п
п —>
00
: Ііт
«->ОО
п + п
Приклад 4. Знайти границю Ііт — зіп
3
2
Гі
и-уоо „
3
+
1
• Розглянемо дві послідовності:
\—г-—\
та
{зіп"^"}.
Перша послідовність нескінченно мала, бо
Ііт • "
я-ко п
3
+
1
І
00
п
3
+1~п
3
П —>
со
= Ііт = Ііт = 0.
я—>°°
/7 я—>°°/2
Друга послідовність обмежена, бо | кіп
3
2"| < 1.
Отже, добуток цих послідовностей є нескінченно малою послідов-
ністю як добуток нескінченно малої послідовності на обмежену.
Звідси Ііт —кіп
3
2" = 0.
Функція
Приклад 5. Знайти область визначення функції
1п(1
+ х)
/(*) =
х-1
• Функція /(х) =
№
^
+
*) визначена,якщо 0,
1
+ х>0,тобто
х-1
якщо х
Ф 1
і х > -1.

264
Глава 7. Границі та неперервність функцій
Область визначення функції /(х) є об'єднання двох інтервалів:
/>(/) =
(-1,1)
II
Приклад
6.
Знайти множину значень функції
/(х) = 2 +
З
8ІП х.
• Врахуємо, що | кіп х | <
1
або -1 < зіп х < 1. Помножимо всі частини
цієї нерівності на 3 та додамо до них число 2.
Маємо
-З < 3$іпх < З,
2-3<2 + 38Іпх<2 + 3,
-1 < 2 + Ззіпд: < 5 .
Отже, £(/) =
[-1,5]
.<
Приклад
7.
Встановити парність
або
непарність
функцій:
г)/(х)
= 2'+2-
х
і
/(х) =
1
8
£±|;
в) Дх) = х
2
+5х.
б) х-3
• У розглядуваних прикладах область визначення кожної з функцій
симетрична відносно точки х = 0 .
а) /(*) = 2*+2-\
Заміняємо х на -х . Отримаємо
/(-*) = 2"+2-<-*>= 2"*+2 *=/(*).
Отже, /"(-*) = /(х) і функція Дх) = 2
х
+ 2~* - парна.
б)
/(х)
=
і
8
£±1.
дг-З
Знаходимо
-х
+ 3
х-3 + 3 V
і
х
+
3
-х-3 х+3 \х-3) х-3
х
+
3
Отже, /(-х) = -/(х) і функція /(х) = І£ непарна.
х-3
в) /(х) = х
2
+5х.
Маємо
Д-х) = (-*)
2
+5(-х) = х
2
-5х.

§1.
Границі послідовностей та функцій
265
Отримали, що /(х), /(-х) #-/(х), отже, функція
/(х) = х
2
+ 5х не є ні парною, ні непарною. Ч
Приклад 8. Знайти періоди функцій:
а
) /"(*) = соз 8* ; б) /Хх) = зіп6х-И§4х.
• а) /(х) = соз8х.
Згідно з означенням періодичної функції
соз8(х + Т)= соя8х,
8(х + Г) = 8х + 2я,
8х + 8Г = 8х + 2я,
8Г = 2я,
т
=
—
.
4
б) /Хх) = кіпбх + 1§4х .
Розмірковуючи аналогічно п. а), маємо, що
для функції /, (х) = зіпбх період Г, = — = — ,
6 З
для функції /
2
(х) = \&4х період Т
2
= — .
Отже, за період Т функції /(х) = зіпбх + Іц4х приймається наймен-
ше загальне кратне цих чисел, тобто Т = я . -4
Границя функції
Приклад 9. Довести, використовуючи означення границі
функції на мові "є - 8", що 1ірп(3х + 2) =5-
• Позначимо у = Зх + 2 .
Задамо довільне число є > 0 і знайдемо таке 8 = 8(є) > 0, що для всіх
х, які задовольняють нерівності
0<|х-і|<8,
виконується нерівність
| у -
51
< є. Для виконання цієї нерівності необхідно, щоб
Є
І
Зх + 2 -
5
< є або
І
х -11 <
—
.
І і З
Звідси 8 =
—
.
З
Якщо тепер для довільного є > 0 і знайденого 8 взяти значення х,

266
Глава 7. Границі та неперервність функцій
що задовольняють нерівності | х -11 < 8, то
|х-і|<5 => |х-і|<| =>|Зх + 2-5|<є =>
\у-5\<г.А
2.x+ 5
Приклад
10. Довести, що Ііт = 2, використовую-
х-»°о X
чи
означення границі функції при х ->
со
.
•
Позначимо у = ^
х +
^
_
Задамо довільне число є > 0 . Знайдемо число М(е) > 0 таке, що для
всіх х, які задовольняють нерівності | х | > М , виконується нерівність
І
у - 21 < є . Остання нерівність виконуватиметься, якщо
2х +
5
0
< є, або
„ 5
Л
< є, або
5
< є, або
2+--2
< є, або
X X X
< є .
Звідси
І
х
І
>
—
. Нехай М =
—
,тоді
є є
\х\>М
X
>•
5
5 2х + 5 „
—
=>
—
< є => 2
є X X
<
є => Ііт у = 2 .А
Розкриття невизначеностей
Невизначеність типу
•<
—
[о
1. Обчислення границь функцій, заданих відношенням двох много-
Р (х)
членів, тобто границь дробово - раціональної функції — -, де Р (х),
0
т
(х) - многочлени степенів п і т , п,т є N , при х
—>
а :
"•«е»^)
Іо.
Виконуємо тотожні перетворення з метою позбавитися від невизначе-
ності, тобто виділяємо в чисельнику і знаменнику множник (х - а), який
прямує до нуля при х
—>
а. Цей множник (х - а) називатимемо критичним.
Далі треба скоротити на цей множник. Якщо при цьому розкладання на
множники виявиться утрудненим, то треба розділити чисельник і знамен-
ник на критичний множник "у стовпчик".

§
1.
Границі послідовностей та функцій
267
При цьому слід пам'ятати:
а) наслідок теореми Безу: якщо а - корінь многочлена Р
п
(х), тобто
Р„(а) = 0,то Р„(х) ділиться на двочлен (х-а) без залишку:
Р„(х) = (х-а)Р
п
_
1
(х);
б) квадратний тричлен Р
2
(х) = ах
2
+Ьх
+
с, у якого дискримінант
В-Ь
2
-
4ас > 0 , представляється у вигляді:
ах
2
+
Ьх + с = а (х - х,) (х - х
2
),
де х,, х
2
- корені квадратного рівняння ах
2
+Ьх
+
с = 0 .
2.
Обчислення границь функцій, що містять ірраціональні вирази:
а) при обчисленні границь функцій, що містять ірраціональні вирази,
які обертаються в нуль при х
—>
а ,в них треба виділити множник
(х-а).
Це можна зробити, позбувшись від ірраціональності в чисельнику або зна-
меннику шляхом домноження дробу на відповідний спряжений множник.
При цьому використовуються формули:
а
2
-Ь
2
= (а-Ь)(а+Ь),
я
3
+Ь
г
= (а
+
Ь)(а
2
-аЬ
+
Ь
2
),
а
3
-Ь
3
=(а-Ь)(а
2
+аЬ
+
Ь
2
);
б) крім того, у багатьох випадках, вирази, що містять ірраціональності,
приводять до раціонального вигляду введенням нової змінної.
3.
При обчисленні границь функцій, що містять тригонбметричні вирази,
виконують тотожні перетворення із застосуванням формул тригонометрії, першу
важливу границю і введений вище ланцюжок еквівалентних нескінченно малих.
Приклад 11. Знайти границі заданих функцій (невизна-
чешсть типу
•( —
>):
X
і
-1
,. х
3
-6х + 4 ... ліх
2
+5-3
а) Ііт— -; б) Ііт—г -; в) Ііт
х
2
+ 5х-6 *-+2 2х
1
-х-6 х-2
Ч
Л/І + X - 1
Ч
,. СОЗ Зх - С08 X . ,.
1-8ІПХ
г) Ііт . —; д) Ііт ; е) Ііт г-.
.Ї^О
+
х
- і
х->о
зіп х
•
агсі§3х (я V

268
Глава 7. Границі та неперервність функцій
• а) Ііт— .
*^х
2
+5х-6
Маємо під знаком границі відношення двох многочленів. Тут не мож-
на застосувати теорему про границю частки, бо границя знаменника дорів-
нює нулю. Підстановка граничного значення х =
1
призводить до невизна-
ченості типу
^ —
>. Розкладемо чисельник та знаменник на множники і ско-
ротимо на (х -1).
х
1
-1 ГО] ,. (х-1)(х + 1) ,. х +
1
2
Ііт-- = і
— Г
=
пт
=
ит
=
—
•
2
+5х-6 Ю) *->і (х-1)(х + 6) х-+іх
+
6 1
.. X
і
-6х
+
4
б) Ьт—г .
*-+2
2х
2
-х-6
Маємо під знаком границі відношення двох многочленів. Тут не можна
застосувати теорему про границю частки, бо границя знаменника дорівнює нулю.
Підстановка граничного значення х = 2 призводить до невизначеності типу
. Розкладемо многочлени в чисельнику і знаменнику за теоремою Безу.
Чисельник х
3
-6х + 4 = (х-2)(х
2
+
2х-2),
бо х = 2 - корінь многочлена, який стоїть в чисельнику, що зумовлює на-
явність множника (х - 2). Далі ділимо х
3
- 6х
+
4 на (х - 2) "стовпчиком".
_2х
2
-6х
2х
2
-Ах
_-2х + 4
-2х + 4
0
Отримали другий множник у розкладі.
Для розкладу знаменника на множники можна поступити аналогічно,
або розв'яжемо рівняння
2х
2
-х-6 = 0
£> = й
2
-4ас =
1
+ 48 = 49 х
12
=-^-; х, = 2, х
2
=--.
6х + 4
х
2
+2х-2
х-2

§
1.
Границі послідовностей та функцій
269
Далі маємо такий розв'язок:
,.
х
3
-6х + 4 ГО] ,. (х-2)(х
2
+ 2х-2) ,. X
і
+2х-2 6
Ііт — -=
{
- \ = Ііт ——;
—-—
= Ііт
-
-
~2
2
х
2
-х-6
10
Л
~2
2(Х
_
2)
Г
+
£| 2х + 3 7
ч
,.
л/х
2
+5-3
в) Ііт .
х->2 х-2
Маємо ірраціональний вираз під знаком границі.
Позбудемось ірраціональності в чисельнику, помноживши чисельник
і знаменник на л/х
2
+ 5 + 3. Далі в чисельнику скористаємось формулою
а
2
-Ь
2
=(а-Ь)(а+Ь),в знаменнику множник л/х
2
+5 + 3 замінимо його
значенням при х = 2 . Отже, маємо
^УТ^-зГої
1іт
(У7^-з)(У7+7+3)
*->2
х-2 10] г->2 (
х
-
2
)(л/х
2
+5+3)
х
2
+5-9 ,. х
2
-4 ,. (х-2)(х + 2) .. х + 2 2
= Ііт = нт = Ііт = Ііт = —.
*->2(х-2)(3
+ 3)
*->2(х-2)-6
*->2 (х-2)-6 *->2 6 З
,
.. л/Г+7-і
г) Ііт .
*-><>
ч71
+ х -1
Маємо ірраціональний вираз під знаком границі.
Спосіб 1. Домножимо чисельник і знаменник на вирази, спряжені до
чисельника і знаменника. Скориставшись відповідними формулами
а
2
-Ь
2
~(а-Ь)(а +Ь), а
3
+ Ь
3
= (а + Ь)(а
2
- аЬ + Ь
2
), маємо
,
чЯ+7-1 ГО] ,.
(7Г+^-1)(л/Г+7
+
1)(і/(1
+ х)
2
+
3
УГ+х~
+
1)
Ііт , — =
<
—
^
= 1іт-
*-*>*/Г+7-і І о і ^
о
(?УЇ+7-і)(л/(і + х)
2
+УЇ+х + і)(4ї+х+і)
,.
(1 + х-1)-3 ,. х-3 З
Ііт -— = Ііт =
—
*->о(1 + х-1)-2
л->ох-2
2
270
Глава 7. Границі та неперервність функцій
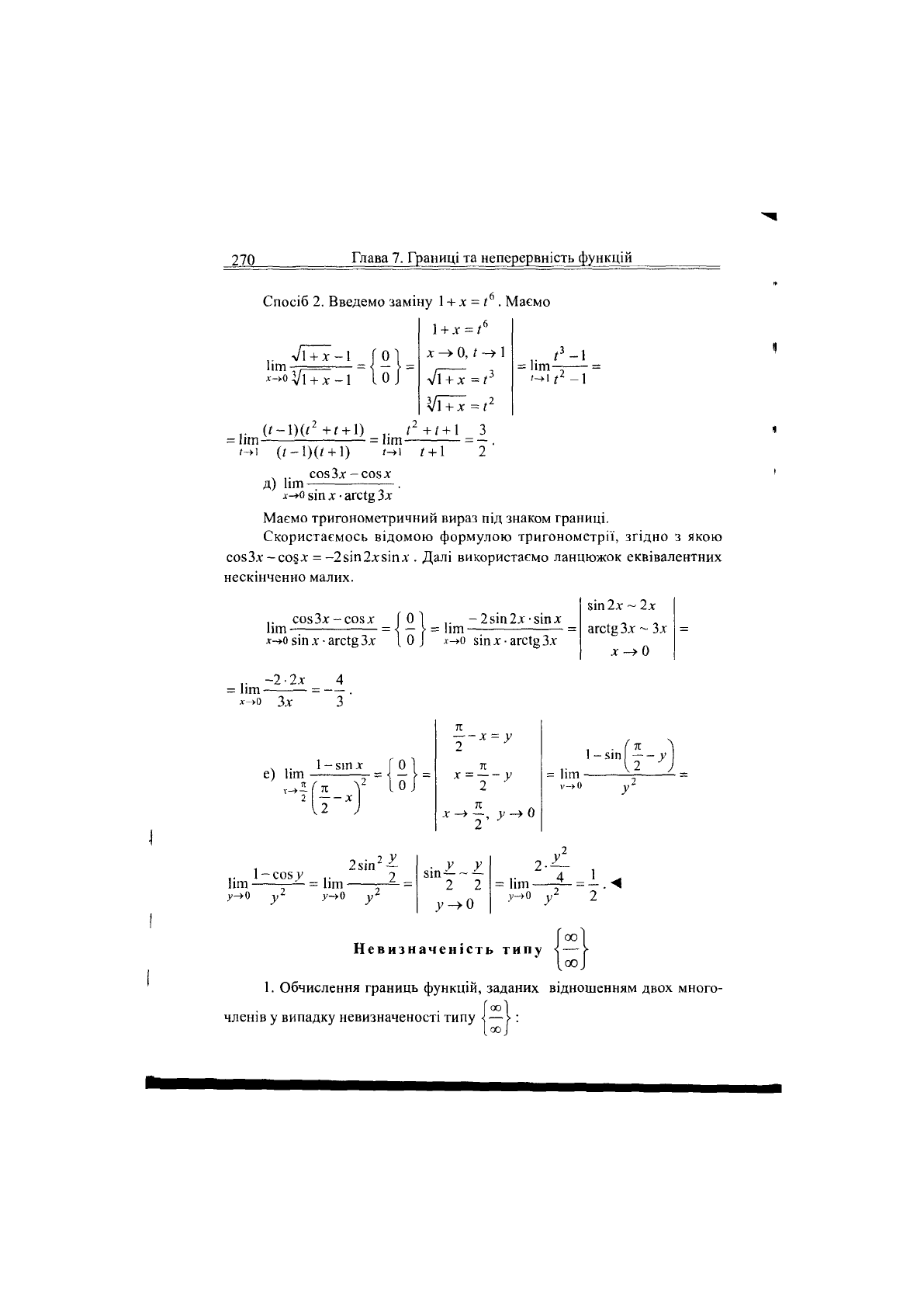
Спосіб 2. Введемо заміну
1
+ х = і
6
. Маємо
УГТ7-1
^>о VI
+
х -1
Пт
=
Ііт = Ііт
\+х
=
Г
х -» 0, і -> 1
^П + X=^
і
+
Х
=Г
7
3
-1
= Ііт
'->і I
і
-1
Г+г +
1
З
ч
,. СОЗЗх-С05Х
д) Ііт-: ~•
*->о кіп х
•
агс(§ Зх
Маємо тригонометричний вираз під знаком границі.
Скористаємось відомою формулою тригонометрії, згідно з якою
сокЗх -со§х = -2$іп2х$іпх . Далі використаємо ланцюжок еквівалентних
нескінченно малих.
,. созЗх-созх Г0І ,. -28Іп2х-8Іпх
1і
т
= \ —
\- Ііт
-
*-»о
5Іп
х
•
агсІ§ Зх
-2 •2х 4
*-»о
8Іп
х
•
агсІ§ Зх
Ііт
зіп 2х ~ 2х
агсІ§ Зх - Зх
х->0
е) Ііт
1
- 81П х
г\\-х
•-х
=
у
71
х=~-у
я
Ііт -
у->0
Ііт
1-С05 у
~~7~
2$іп
2
^
=
Ііт -
у->0
• У У
81П—~ —
2 2
у-+0
2-'
Ііт
-
оо
Невизначеність типу <
І
—-
1. Обчислення границь функцій, заданих відношенням двох много-
Г°о]
членів у випадку невизначеності типу
