Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§
1.
Границі послідовностей та функцій
271
а) у чисельнику і знаменнику виноситься х у найвищому степені. Після
відповідних скорочень, та враховуючи, що дроби типу
—>
0 при х
—><»,
отримуємо значення розглядуваної границі;
б) використовуються еквівалентні нескінченно великі, тобто
Р„{х) = а
0
х" +
а^х"'
1
+ ...+ а
п
~ а
й
х" ,
()
т
(х) = Ь
0
х
т
+Ь
]Х
т
~'
+ ...
+
Ь
т
~Ь
0
х
т
при
х->оо.
Тоді
Ііт
а
п
х +а,х +...
+
а
= Ііт— • :
—
=•!
0 при п
<
т,
а
0
при п = т,
оо при п > т.
2.
При обчисленні границь дробів, що
МІСТЯТЬ
ірраціональність, вико-
ристовуються аналогічні прийоми.
Приклад
12. Знайти границі заданих функцій (невизна-
ченість
типу
<|
—|>
):
оо
ч
,. 2х
2
+х
+
1
а)
Ііт — -
*->°°5х
-х-А
в)
Ііт
2х
5
+ 3х
3
- Ах
*->-°°
Зх -4х + 2
б)
Ііт
10*-З
2х
3
+ 4х
3
+ З
.
(Ух
2
+1+х)
2
г) ьт
—ТГ—=—;
д)
Нт
1п(Зх
3
+4х
+ 5)
іп(2х
9
+ х
3
+1)
а) Спосіб 1.
,. 2х
1
+х + \
Ііт —-
5х -х -4
=
<
—
>
= Пт
хЧ 2 + - + —
X
х
1
ї-юо 2І - 1 4
х
І
5 ~
х х
г
2 + 0 + 0 _2
5-0-0 ~5
272
Глава 7. Границі та неперервність функцій
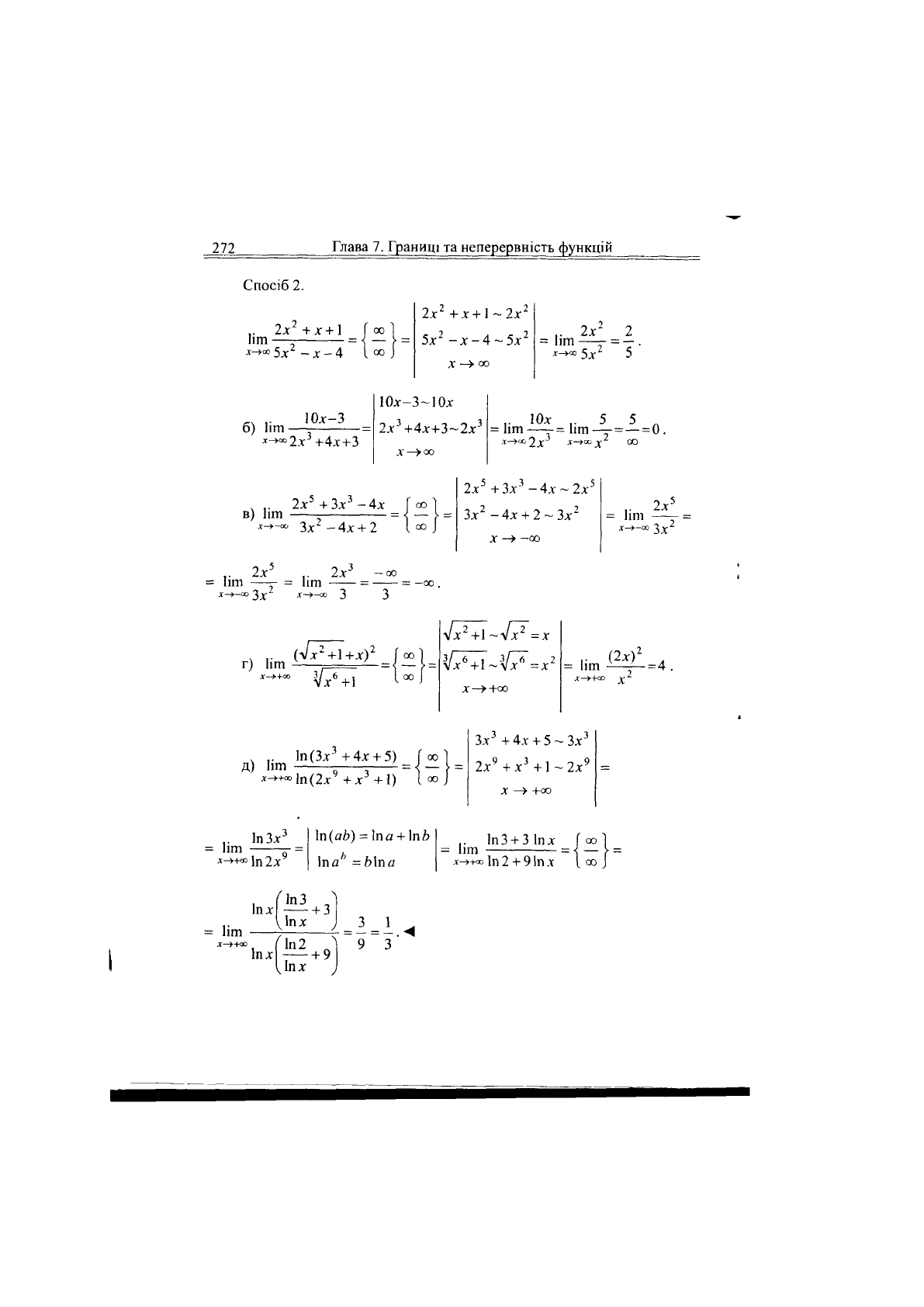
Спосіб 2.
Ііт
їх
1
+х+\
х
^
х
5х
г
-х-4
їх
1
+х
+
ї ~2х
2
5х
2
-х-4~5х
2
X
-> оо
= Ііт
їх*
5х
б) Ііт-
10х-3
*->
ж
2х +4х+3
10х-3~Юх
2х
3
+4х+3~2х
3
х—>оо
.. Юх .. 5 5
=
Ііт—-= Ііт—=— = 0.
*-><»2х
і->оо
х
00
в) Ііт
2х
5
+ 3х
3
-4х
Зх"-4х + 2
2х
5
+3х
3
-4х~2х
5
Зх
2
-4х + 2~3х
2
,. 2х
5
Ііт ——
х
^-<» Зх
2
,. їх* ,. 2х
3
-оо
= Ііт —- = Ііт = = -оо.
х-^~сс2х
*->-«>
з з
г) Ііт
(л/х
2
+1+х)
2
Х-++СО 3/ 6
х°+1
Л/Х
2
+1~Л/Х
Т
=Х
4?7\~47=х
2
х—»+оо
Ііт
(2х)
2
= 4 .
д) Ііт
1п(3х
3
+4х + 5) оо
дс-»-+оо
1п(2х
9
+х
3
+1) І 00
Зх
3
+ 4х +
5~3х
3
2х
9
+х
3
+1 ~2х
9
х
—>
+00
= Ііт
ІпЗх
3
1п2х
\п(аЬ) = 1пд + 1пЬ
Іпа* = Ь\па
= Ііт
ІпЗ +
3
Іпх
*->+<»
1п
2 + 91п х
1пх(-^- + 3
Ит
іпх )1Л.*
Іпх
1п2 „
Л
+ 9
ч
1пх
9 З

§
1.
Границі послідовностей та функцій
273
Невизначеність типу
{0-оо}
Невизначеність типу {0
•
оо}
шляхом тотожних перетворень зводять до
0 І с
Г
00
невизначеностей типів -і —
>
або
<
—
0 І 1 оо
Приклад
13.
Знайти границі заданих функцій
(невизна-
ченість типу
{0
•
оо
}
а)
Нгп
х
•
зіп
—г-',
б) Ііт •і%х.
• а) Ііт х-зіп — =
{оо-0
} =
81X1
->0
2 2
X X
= Ііт х
•
-ї— = Ііт
—
= 0;
Х->00
X X—>00 ДС
б) 1іт[ —-х =
{0-оо}=
Ііт—
X -81ПХ
созх
•
я
і
81П
— = І
2
X
=
Ііт-2
созх
2
81П_У
~
_у
.у->0
Я
я
х=--^
X -> —, V -»
О
2
= Ііт
у->0
я
соз
І
—
- у
• Ііт
У->0 8ІП^
Ііт ^ = 1. <
у-+0 у
Невизначеність типу { оо
—
оо }
Невизначеність типу
{оо
-
оо
}
шляхом тотожних перетворень зводять
до невизначеностей типів | | або | — |. При цьому у випадку наявності
ірраціональності чисельник та знаменник домножують на відповідний спря-
жений множник.

274
Глава
7.
Границі
та
неперервність функцій
Приклад
14.
Знайти границю заданої функції (невизна-
ченість типу
{оо
-
оо
}):
Ііт
(ліх
1
+
8х +
3
-л/х
2
+4х-5).
•
Ііт (л/х
2
+ 8х
+
3
-л/х
2
+
4х-5)
=
{
оо
—
оо
>
=
,. (7х
2
+ 8х +
3-л/х
2
+
4х-5)(л/х
2
+ 8х +
3+л/х
2
+ 4х-5)
Ііт
.
4
х
^
+а0
л/х
2
+8х
+ 3+л/х
2
+4х-5
х
2
+8х
+
3-х
2
-4х
+
5
,. 4х + 8
Ііт =====•=
пт
л/х
2
+8х
+
3
+
л/х
2
+4х-5
^
+00
л/х
2
+ 8х +
3+л/х
2
+ 4х-5
х
2
+
8х + 3~
х
2
х
2
+
4х-5~х
2
4х +
8
~ 4х
X
—> 00
=
Ііт ^
Х
= Ііт — =
—= 2.-^
дг->+« X + X
дг->+оо
2х 2
\|/(лг)
Обчислення границь вигляду
1іт[ф(х)]
Нехай
1іт[ф(х)Г
м
=С.
Слід мати
на
увазі,
що
1) якщо існують скінченні границі
Нт ф(х)
= А і Ііт
\у(х)
= В ,
Х~>А Х—*А
тоС=/;
2)якщо
Нт
ф(х)
=
АФІ
І Ііт у(х) =
±оо
, то
питання
про
знаход-
.х-»а
Х—>А
ження границі розв'язується безпосередньо піднесенням
А в
степінь
+00
або
-оо ;
3)якщо Нтф(х)
=
1
і Нт
\у(х)
= «,
то маємо невизначеність типу
Х~Т Х—>А
а) для розкриття невизначеності використовується друга важлива гра-
ниця, яка має вигляд
Ііт
(і
+ — 1
= Ііт
(1
+ а)
а
= е.
Х-*<Х\
х) а->0

§
1.
Границі послідовностей та функцій
275
Дійсно, поклавши ф(х) =
1
+ а(х), маємо
Г _!_ 1 "М'ЧЧ*) Ііт а(х)Мх)
С= 1іт[
Ф
(х)]
¥(дг)
=
\іт\[1+а(х)]
а
^
Ііт [ф(х)-1]\}/(х)
= |а(х) =
ф(х)-1|
= е
х
- ;
б) для розкриття невизначеності використовуємо таке представлення:
[ф(х)Г
М
=
е^»
1
"^»
і використовуємо еквівалентність 1п(1+а(х))~а(х), а(х)—>0 при х-»а ,яка
є наслідком другої важливої границі.
Тоді
Ііт У(
х
)
|п
(
|+а
(
дг
))
С
= Ііт
Мх)Г
(х)
= Ііт
е^
1
"**)
=
І
Ф
(х) =
1
+
а(х)
І
= е"'
х—їа
Ч(х)а{х)
Ііт
Ііт М*)-1]ч<(*)
•е
х
^
а
= | а(х) = ф(х) -
1
| = е
х
^
а
Отримали той же результат, що в п. а).
або
4) якщо Ііт ф(х) =
оо
і Ііт у(х) = 0,
Х—>А Х—>А
якщо Ііт ф(х) = 0 і Ііт \|/(х) = 0,
Х—>А
Х-*А
то маємо невизначеності типів {°°
0
} або |о
0
} відповідно.
Для .розкриття цих невизначеностей використовують представлення
[ф(х)Г
(д)
=
е
^
х)Хт(х)
.
Приклад 15. Знайти границі заданих функцій:
2
2х
ч
,. (зіп2хУ
+
* ( х + 1
Л
*
а) Ііт
|
| Ііт
(-.
5) х-*х> у 2х +1
в) Ііт
Злг+1
л
; г) Ііт(2е
х
'
1
-І)-
1
•
а) Ііт
.
( зіп2х
У
+Дґ
іт
-><Ч х )
5Іп2х ~ 2х
х->0
= Ііт
*-»0^
X )
2=2

276 Глава 7. Границі та неперервність функцій
б)
Іітр^-У
=
Х
+ \~ X
2х
+1
~ 2х
X —>
00
=
іі
т
Г^Т
2
=
іі
т
ГіТ
2
=
х^>™\2х
)
х-^<и\2
)
= 0.
в) Спосіб 1.
'
^
={Г}= 1іш|'і
+
— Г*'*
^
2х -
3 у дс-х»^
2х-3
..
( 2х
Ііт
= Ііт
1
+
= Ііт
х-*юу 2х — 3) х->оо
2-5*
1
+
-
2х-3
3(2-5*)
:
Ііт е
2
*~
3
=
*—>со
,.
3(2-5*) ,. -15* 15
Ііт
— Ьт -
Спосіб 2.
*->°°у2х-і]
= е
(2-5^)1п^-
(2-5*)1п
= Ііт е
2х
~
3
= Ііт е
Х~>С0
Л—>00
(2-5*)1п
1+
= Нт е
1 2х
~
3
х-»<ю
V 2х-3у 2х-3
З
х ->
оо,
>
О
2х-3
Ііт
(2-5л)-3
15
о
г) 1іт(2е*-' -1)^
= {і°°}=
Х-1
= 2
X
= 2 +
1
X
-»
1,
2 ->
О
2е*
_І
-1 = 2е
г
-1
= 1іт(2е
г
-1)
2
={Г}= Нт(1 + 2е
2
-2)
г
= 1іт(1 + 2(е
г
- І))
2
=
2->0
2->0
2-*0
Є~ -
1
~ 2
2-»0
= 1іт(1 +
22)
2
=Нт(1 +
22)
2г
=
е
12
.-«
2-+0
2-»0

§1.
Границі послідовностей та функцій
277
Порівняння нескінченно малих
Приклад 16. Порівняти нескінченно малі функції сх(х) та
Р(х) при х
—>
0 :
а) сц» = 5х
2
+ 2х
5
, р\х) = Зх
2
+ 2х
3
;
б) а(х) = х
8Іп
2
х, р\х) = 2х
8Іп
х;
в) а(х) = х
•
їпГі
+
х
)' Р(*)
= х 8т х
•
• а) а(х)
=
5х
2
+
2х
5
, Р(х) = іх
2
+ 2х
3
, х -> 0.
,з
а(х)
Ііт = Ііт
5.т
2
+ 2х
5
=
Ііт
X
І
(5+ 2*0 ,.
5 +
2х* 5
1іт
:
= -#0.
+ор(х) х-*0 3х
2
+2х
3
*~>°
х
2
(3 + 2х) *-*о 3
+
2х З
Отже, а(х) та Р(х) - нескінченно малі одного порядку при х
—>
0 ,
тобто а(х) =
0(р(х)),
х -» 0.
б) сс(х) = хзіп
2
х, Р(х) = 2х8Іпх, х->0.
,. а(х) .. х8Іп
2
х ,. зіпх
• Ііт—
1
-
£
= 1іт = Ііт = 0.
ї->ор(х) Г->0 2Х8ІПХ -Ї->0 2
Отже, а(х) - нескінченно мала вищого порядку, ніж Р(х) при х
—>
0 ,
тобто а(х) = о(Р(х)), х
—>
0.
в) а(х) - х
•
1п(1
•<-
х), Р(х) = хзіп х, х -» 0 .
1п(1
+ х)-х
зіпх~ х
х-»0
,. а(х) ,. х1п(1 + х) ,.
1п(1
+ х)
Ііт —— - Ііт
1
= ит -
*-*о р(.ї) х-*0 хзіпх л-»0 зіпх
=
Ііт —=
1.
х-*о
х
Отже, а(х) та р(х) - еквівалентні нескінченно малі при х
—>
0 , тоб-
то
а(х)
~
Р(х),
х 0. Ч
Приклад 17. Визначити порядок малості к нескінченно
малої функції а(х) відносно Р(х) - х при х -» 0:
а) а(х)
••=
2х - Зх
3
+ х
5
; б) а(х)-^л/і + х
2
-л/і-х
2
;
в) а(х) =
л/Т-
4х - л/і - Зх ; г) а(х) = і§ х - зіп х

278 Глава 7. Границі та неперервність функцій
• а) а(х) = 2х - Зх
3
+ х
5
= х(2 - Зх
2
+ х
4
), тому
а(х)
2х-Зх
3
+Х
5
..
2
4ч , п
Ііт —— = Ііт = 1іт(2 - Зх + х ) = 2 * 0,
л-->0 X А->0 X >->о
тобто а(х) = 2х - Зх
3
+ х
5
= О(х), х
—>
0, порядок малості к = 1.
б) а(х) = л/і+х
2
-\/і-х
2
=
-4\'Х
2
)(4\ + х
2
+Л/І-Х
2
)
2х
2
л/і + х
2
+л/і-х
2
л/і + х
2
+л/і-х
2
,. а(х) ,. л/і + х
2
-л/і-х
2
,.
нт —— = Ііт = ііт
і->0
X
і
*-»<>
^ч
2
(7ї7І
2
"+л/іТ7)
= 1*0,
тобто а(х) = л/і + х
2
- л/і - х
2
= 0(х
2
), х -> 0, порядок малості
&
= 2 .
Очевидно, що \/і +г
2
-Л/І
-х
2
~ х
2
, х
—>
0, бо Ііт
а
^ =
1
.
х-»0
в) а(х) = л/і-4х-л7і-3х =(л/і-4х-1) + (1-
3
л/і-3х) =
-4х
Зх
>/і-4* +
1 1
+ ч/і-3х+г/(1-3х)
2
,. а(х) ,. VI-4х -чУі-Зх
Ііт = Ііт
ї->0
X *->0
= Ііт
= -2 +
1
= -1
л/і-4*+1
1
+ Уі-Зх+}/(1-Зх)
2
Отже, ця функція першого порядку малості відносно х і еквівалентна
(-х): а(х) =
Л/І-4Х-Л/І-ЗХ
= О(х), х -> 0, £ = 1;
а(х) = л/Т^ЯТ-^І-Зх ~-х, х->0.
г) а(х) = 1§х-зіпх = 1§х(1 -соях) = 1§х-2$іп
х _1.
2 ~ 2
х\ х->0.
1іт
^)
= 1
і
т
І^!^
= 1іт
*-»о х
3
х
3
~
х
1
^-
=
1*0.
л-^о
х-
1
2
„3>
Отже, а(х) =
1§
х - зіп х = 0(х ), х
—>
0, к = 3 - порядок малос
гі.
-4

§1.
Границі послідовностей та функцій
279
IV. Задачі для практичних занять
Послідовність. Границя послідовності
7.1.
Написати п'ять перших членів послідовності
{х
ГІ
}.
а)х
я
=1 +
(-і)"і;
б)х„=/і(1-(-1)
и
); в)х
п
=^-.
п 2л - З
7.2.
Записати формулу загального члена х
п
послідовності.
а)--,
-, б) 0, 2, 0, 2,...
2 3 4 5
,.468
7.3.
Користуючись означенням границі послідовності, до-
вести, що
ч
.. Зл-2 3 ^ ,. 4п
2
+1 4
а) Ііт = —; б) Ііт —= = —;
«->«>
2п -1 2 «-»*>Зп +1 З
2-Зл
2
З
в) Ііт
"->
(ю
4 + 5л 5
У задачах 7.4 - 7.30 обчислити задані границі.
_ . .. л-1 _ _ ,. 5л + 1
7.4. Ііт . 7.5. Ііт
н-юо
2>п
. «->'» 7 - 9п
щ
, .. (л + 1)
2
,. Зл
2
-7л + 1
7.6. Ііт- ~. 7.7. Ііт г-.
"-»*> 2п
"->°°
2 - 5« - 6«
„. .. л
3
-100л
2
+1 „
п
,. 1000л
3
+3л
2
7.8. Ііт ; . 7.9. Ііт-
»-»» 100л
2
+15л ' »->»0,001л
4
-100л
3
+1
,
1П
.. (л + 1)
3
-(л-1)
3
_
ЛЛ
,. (л + 1)
4
-(л-1)
4
7.10. Ііт- -— '—. 7.11. Ііт ' '
„->» („ + І)
2
+ (
И
_ І)" п->со („
+
І)
4
+ (
П
- 1)"
_.. л/л
3
+2л-1 _ ,. \п
2
+п
7.12. Ііт . 7.13. Ііт .
н->°о П + 2 л-><ю Л + 1
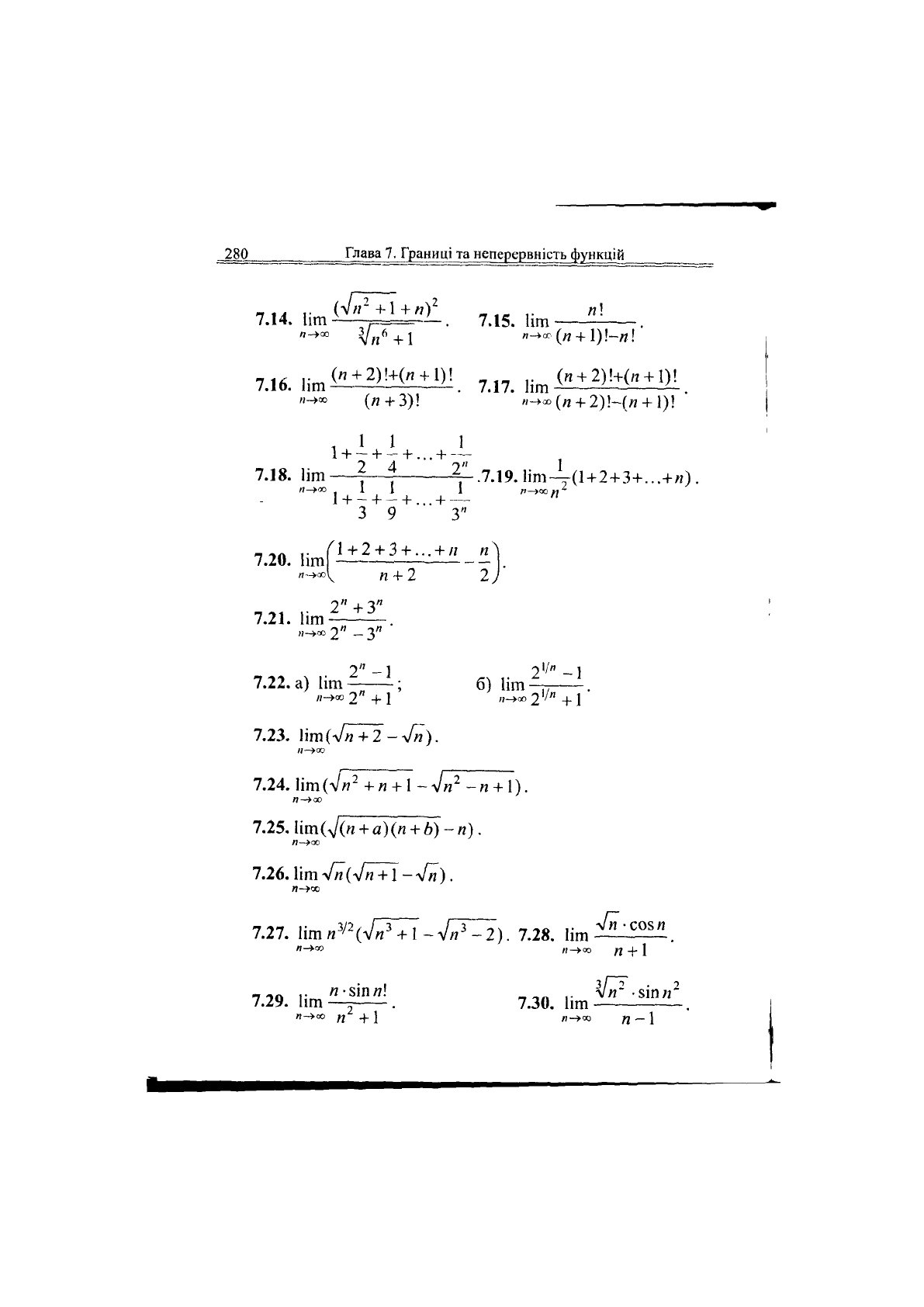
280
Глава
7. Границі та
неперервність
функцій
...
,. (V//
2
+1
+п)
2
,. п\
7.14. Ііт-—-===-—. 7.15. Ііт
у[п
в
+ \
"-»<*(/*
+1) !-л!'
7.16. 1іт^^±^. 7.17. 1іт^±^^
»->°° (л + 3)! »->»(я + 2)!-(я + 1)!
,11 1
7.18. Ііт \-~ Ц- .7.19.
Ііпі—(1+2+3+...+п).
Я->00
,11 І Л->00
1
+ - + - + ... + — "
3 9 З"
7.20. Ііт
И--»00
7.21.
Ііт
'І +
2
+
З
+ ... + я
V
П + 2 2;
2"+З"
я
-,п '
я-»»
2" - З
2"
-1 2
,/
" -1
7.22. а) Ііт— ; б)
Ііт-г;
/,-*Х)
2" +1
,,->ао2
|
/
л
+і
7.23.
1іт(л/« + 2 - л/л).
7.24.1іт(л/«
2
+« +
1
-л/и
2
-и +1).
7.25.1іт(лДи+
«)(«
+6) -
п).
я-»оо
7.26. Ііт л/м(л/я +
1
- л/л).
Я-»0О
7.27.
1ітй^(л/7^Т-л/^
Г
Г2).
7.28. Ііт^'
005
",
я-»» п->оо И + 1
__
0
,. «-8іп«! Мп
2
-&іпп
2
7.29. Ііт— . 7.30. Ііт
п-»со /2 4-1
л
_»оо я —1
