Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§
1.
Границі послідовностей та функцій
281
Функція
7.31.
Знайти область визначення функцій:
а) /О) = ^4- X
і
+ —;б) /(де) = агссоз^ -1 ^;
в)я*)=-Ц^-.
СО§2х
7.32. Знайти множину значень функцій:
а) Дх) = |*| +
1
;б) Дх) = -х
2
+8х-13;
в) Дх) =
1-Зсозх.
7.33.
Знайти функцію, обернену даній:
, 1
а)_у = 1-3х; б)>- = х^+1; в)у =
-
;
1-х
г) у = х
2
-2х; д) у = \0
х+
, е) .у =
1
+ 1§(х + 2);
є) у =
1о§
х
2\ ж) у - 2 зіп Зх.
7.34. Встановити парність або непарність функцій:
а
) /(*) - *
4
зіп 7х ; б) /(х) = х
4
- Зх
2
+ х;
в
) /(
х
) =
І£
С08
*
•
7.35. Довести, що /(х) + Д-х) - парна функція, а
Дх)-/(-х) непарна функція.
7.36. Довести, що добуток двох парних функцій є парною
функцією, добуток двох непарних функцій - парна функція, до-
буток парної і непарної функції - непарна функція.
7.37. Знайти періоди функцій:
а)/(х) = зіп5х; б) Дх) = 1§соз2х;
в
) /(
х
) - І£3х + соз 4х.
7.38. Побудувати графік такої періодичної функції з періо-
дом Т - 1, яка на інтервалі [0,1) задана формулою:
а) у - х; б) у = х
2
.
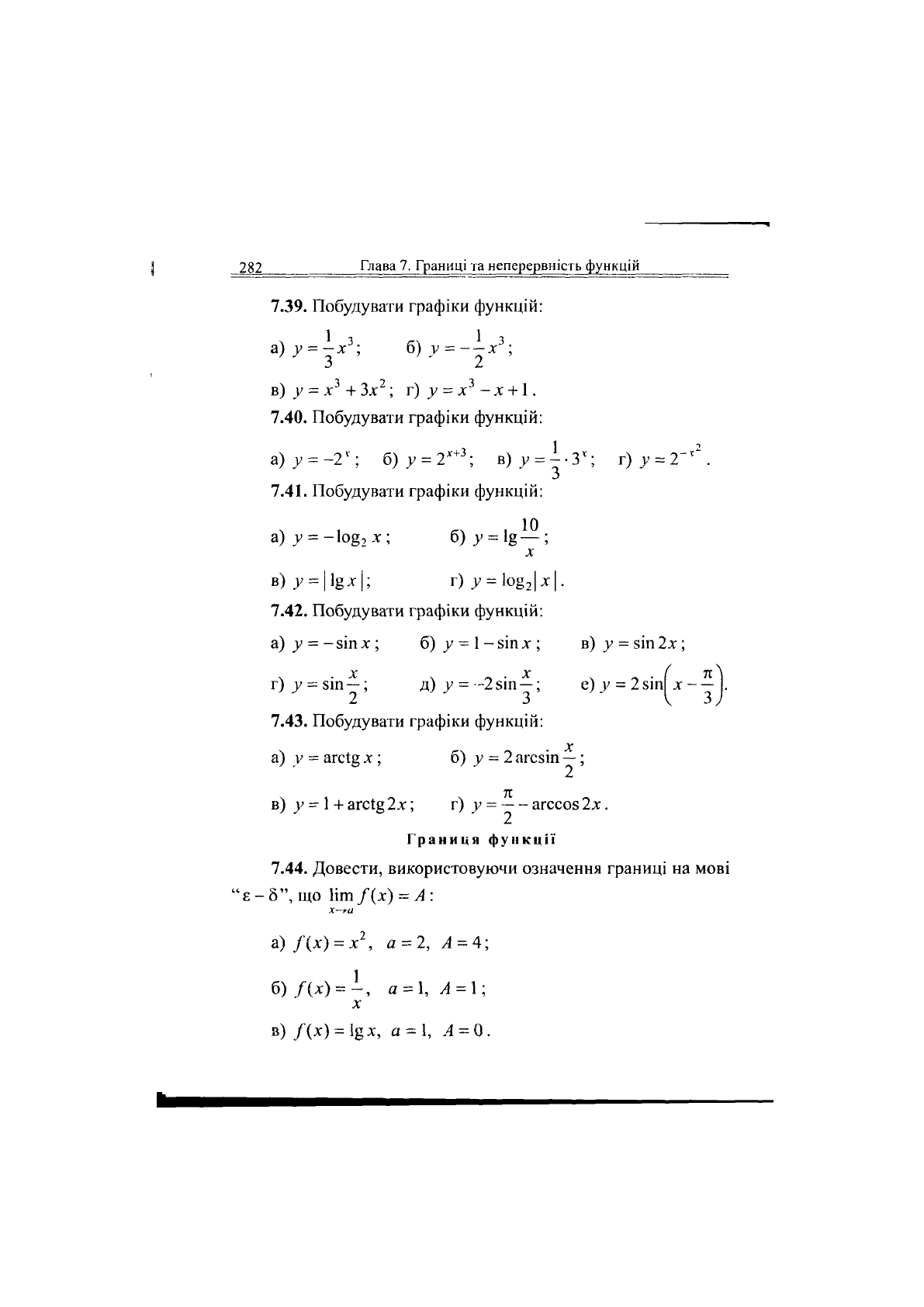
282 Глава 7. Границі та неперервність функцій
е) у = 2зіп^х-^.
г)у = $\п^; д)
>>
= --2$іпу;
7.43.
Побудувати графіки функцій:
х
а) у = агсі§ х ; б) у = 2 агсзіп —;
К
в) у =
1 +
агс!§2х; г) у -
—
- агссоз2х.
Границя функції
7.44. Довести, використовуючи означення границі на мові
"є-8",
що 1іт/(*) = Л:
а
) /(*) = х
2
, а = 2, А = 4;
б) /(*) = -, а = \, А = \;
х
з) Дх) = 1
8
х, а = 1, .4 = 0.
7.39. Побудувати графіки функцій:
л 1 3 (Г\ Із
а) У = -х ; б) у = --х ;
в) у - х
3
+ Зх
2
; г) у = х
3
- х + 1.
7.40. Побудувати графіки функцій:
а)у = -2
х
; 5)у = Г
+і
; в)^ = 1-З
т
; г)у = 2^
2
7.41.
Побудувати графіки функцій:
а)>> = -1о§
2
х; б)у = І£—;
х
в)_у = |і§х|; г)
_у
= 1о§
2
| х І.
7.42. Побудувати графіки функцій:
а)ту = -зіпх; б)>>-1-5Іпх; в)у = 8Іп2х;
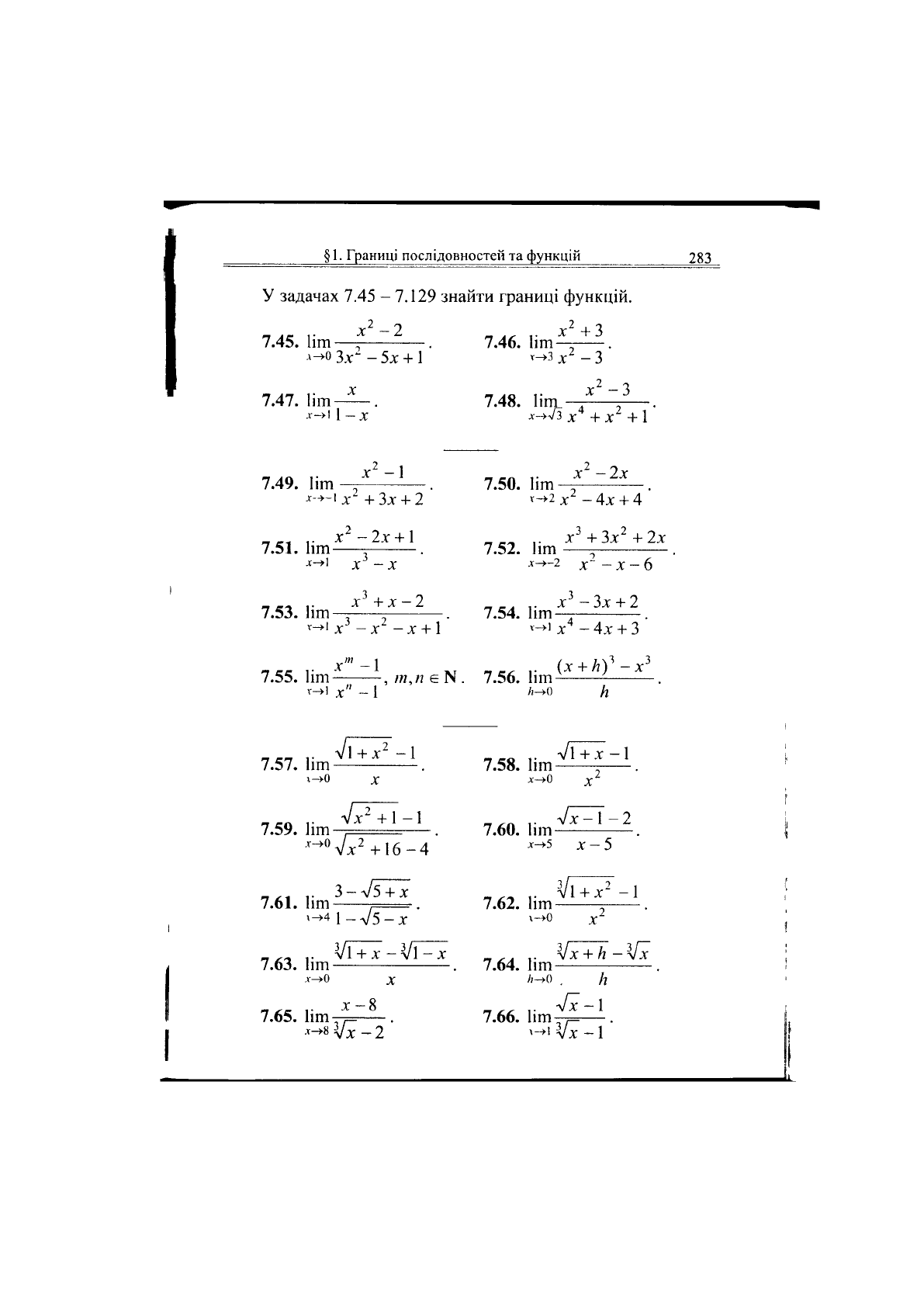
§1.
Границі послідовностей та функцій
283
У задачах
7.45
-
7.129
знайти границі функцій.
х
2
- 2 х
2
+ З
7.45. Ііт— . 7.46. Ііт— .
*-х>ЗдГ-5*
+
1
^з
х
2
_з
7.47. Ііт—. 7.48. Ііт ^ ~
3
.
*->І1-Х
*->73дг
4
+х +1
х
2
-1 х
2
-2х
7.49. Ііт-= . 7.50. Ііт
X
і
4-Зх 4-2 *->2 х
2
-Ах + 4
х
2
-2х +
1
,. х
3
+3х
2
+2х
7.51.
Ііт
;
. 7.52. Ііт
л-*
1
X
3
- X х->-2 х
2
- X - 6
х
3
+х-2 х
3
-Зх + 2
7.53.
Ііт—; г . 7.54. Ііт-
х
3
- х
2
- х 4-1 х
4
- 4х + З
_
__ .. х
т
-1
ЖТ
_ _, ,. (х +
/г)
3
-х
3
7.55. Ііт , т,п єN. 7.56. Ііт
г-И
х
" -1 «-»о Н
„
С
„ ..
Л/1
+
Х
2
-1
„ ^
0
,. А/І 4-Х -1
7.57. Ііт . 7.58. Ііт - .
_
... ,. л/х
2
4-1-1 ^
п
л/х-1 -2
7.59. Ііт , = . 7.60. Ііт-
х->0
л/х
2
4-16-4
..
З-л/54-Х
_ _„ ,. л/і 4- х
2
-1
7.61.
Ііт , 7.62. Ііт
1
- л/5-х ' ' " *-*о
X"
_
,. л/і + х - л/і - х ,.
л/х
4- /г -
л/х
7.63.
Ііт . 7.64. Ііт
х->0
х А->0 . /ї
7.65. Ііт * ^ . 7.66. Ііт ^=—-.
*-»8
л/х-2 л/х-1
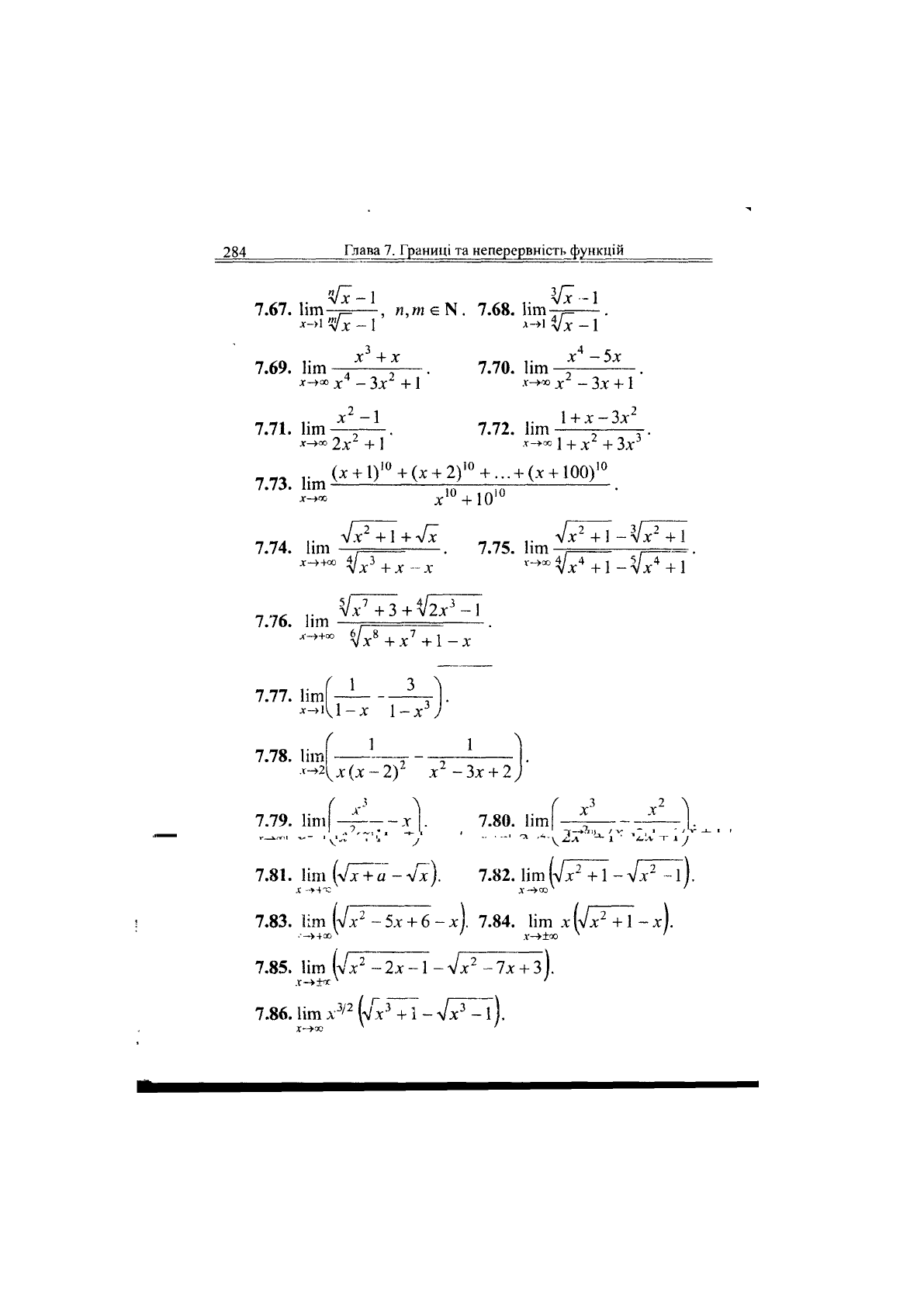
284
Глава 7. Границі та неперервність функцій
_ ,. л/х-1 ... _ ,„ ..
Ух
- І
7.67. Ііт—==—,
п,те?і.
7.68.
Ііт-7=—
7.69. Ііт
х +х
*->°°
х
4
- Зх
2
+
1
7.70. Ііт
х
4
-5х
7.71.
Ііт
х
2
-1
2х
А
+1
7.72. Ііт
*->°°х -Зх + 1
1 + х-Зх
2
1
+ х
2
+ Зх
3
773
Ііт (* + 1)'
0
+(* + 2)
і0
+ .- +
(-У
+ 100)
10
' *-*» х
10
+ 10
10
Ч10
„„.
.. л/х
2
+1 + л/х „„„ .. л/х
2
+1 -л/х
2
+1
7.74. Ііт ,. . 7.75. Ііт . =====
^х
3
+ х - х
г
^ ^х
4
+1 - V*
4
+ 1
7.76. Ііт
5
4х
1
+3+
4
42х
Г
~\
X
+ х +1 - X
7.77. Ііт
х-*1
( 1
1-х 1-х
3
7.78. Ніг/
1
.ї->2
1
^х(х-2) х -Зх + 2
7.79. Ііт
X
[.
7.80. Ііт
~ї *Ґ»]} /"V "І / V
^ '^-у^л. 1 ' -г і у
7.81. Ііт (л/х +а - VI). 7.82. Ііт (л/х
2
+1 - Тх
2
"Т).
7.83.
Ііт (л/х
2
-5х + 6-х). 7.84. Ііт х^х
2
+1 - х).
7.85.
!іт (л/і^2дг-1-л/х^7]ГГз).
7.86. Ііт х
3/2
(/х
3
+1 - л/х
7
^ 1),

§1.
Границі послідовностей та функцій
285
_ ,. ЗІпЗх
7.87. Ііт
*->0 X
7.89. Нт
і%2х
7.91.
Ііт
х->0
зіп 5х
2х - агсзіп х
*-+о 2х + агсІ§ х
7.93.
Ііт
1 - СОЗ X
7.95. Ііт
х->0
7.97. Ііт
*->о хзіп2х
1 + зіпх-созх
*->о
1
- зіпх - созх
(1 - соза)
2
а-»о
1§
3
а-зіп
3
а
7.99. Ііт
я ґ
1 - зіп X
дг->—
2
Я
\
- X
7.101.
Ііт
{-
Л2
*§Х
7.88. Ііт^.
х-+0
Х
_
_ _
.. 2 агсзіп х
7.90. Ііт
*->о Зх
1 - созх
7.92. Ит
*-»° X
і
7.94. Ііт
а
^°і/(1-соза)
2
•
_~, .. Іеа-зіпа
7.96. Ііт — г
7.98. Ііт
*->о
а->0
ґ
І 1
Л
^зіпх і§х
7.100. Ііт
созх
^О-зіп*)
2
7.102. Ііт
зіпа
а
7ГХ
х->1
7.105. Ііт
созх - зіпх
.ч
соз2х
~ . у-а . пу
.у—>я
51П
X
7.106. Ііт
2 "2а
я
л/3
6
созх
2
7.107.
Ііт
1 + -
V х)
7.108. Ііт
/->оо
Г.-і]'
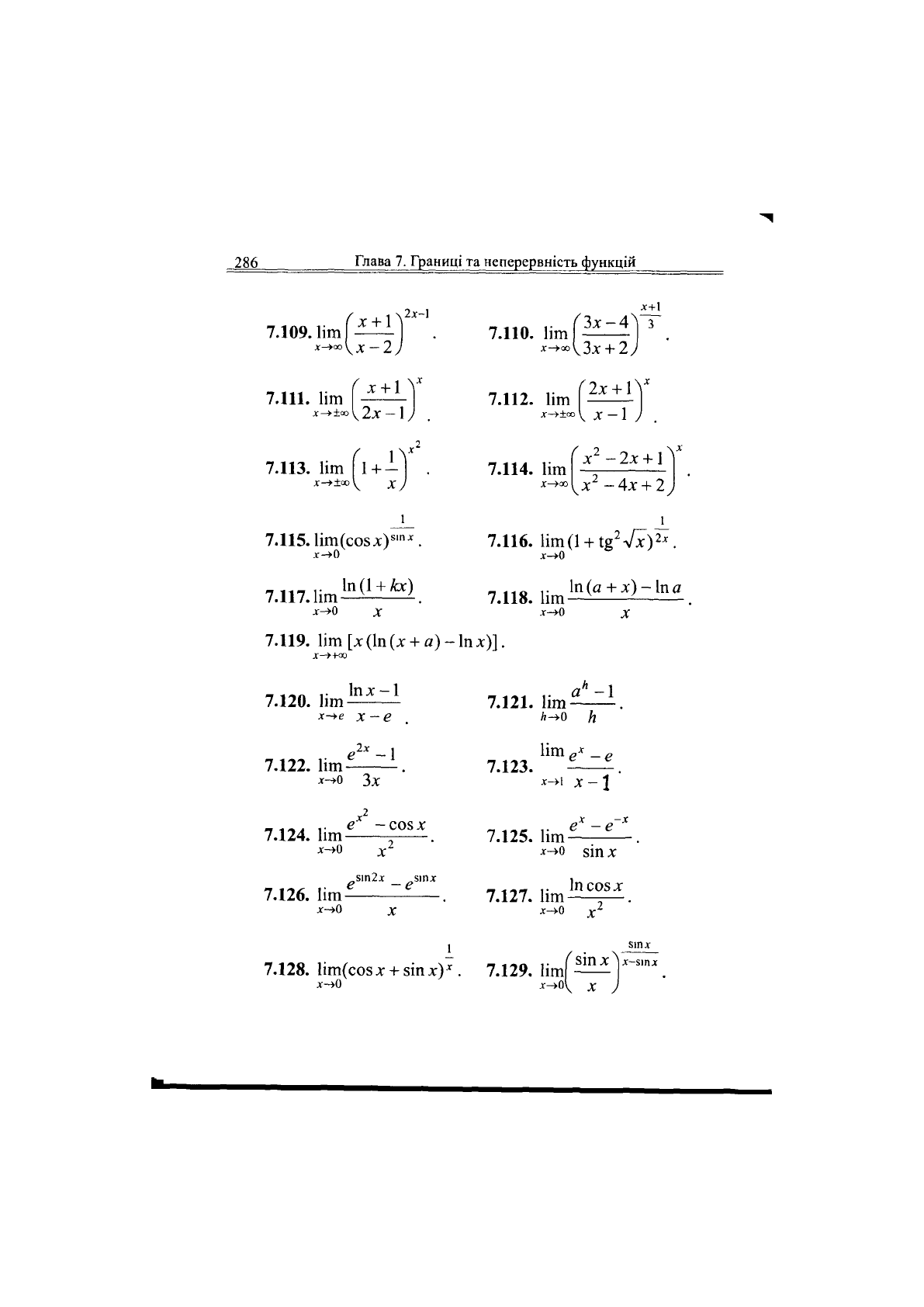
286
Глава 7. Границі та неперервність функцій
7.109. Ііт
Гх +
1
2х-1
7.111. Ііт
х->+°о
ґ х
+ 1
V
у2х-1у
7.110.
7.112.
Ііт
х->оо
х+1
Ііт
х-»±°о
Зх + 2
2х + П
V х -1
7.113. Ііт
X—>±0О
( 1
ч
*
1+-
7.114.
Ііт
X—>00
Г
х
2
-2х + Г
х
2
- 4х + 2
7.115.1іт(со8х)
х->0
1_
81ПХ
7.117. Ііт
1п(1 + Ах)
7.116. 1іт(1 +
і§
2
7х)
2
^,
х->0
х->0 х
7.119. Ііт
[х(1п(х
+ а)-1пх)].
7.118.
1іт
1П(а
+ х)
--^
х-+0
_ .. Іпх -1
7.120. Ііт
х-+е
Х-Є
7.122. Ііт
. е
2
*-1
*->о Зх
7.124. Ііт ---
х->0
7.126. Ііт
х->0 х
7.121. Ііт
. а
л
-1
7.123.
7.125.
7.127.
1іт
е
*
_
е
х->і д: - 1
..
е
х
-е~
х
Ііт
*->о ЗІП X
,. ІПС05Х
Ііт
х-*0
2
7.128.
1іт(соз
х +
зіп
х)
х
. 7.129.
х->0
81ПХ
,. ( ЗІП X
ІХ-5ШХ
нт
*-><\
х

§1,
Границі послідовностей та функцій 287
Порівняння нескінченно малих
7.130. Довести еквівалентність нескінченно малих функцій
а(х) і Р(х) при х -» 0:
а) а(х) =
1п(1
+ 5х), р(х) = е
5х
-1;
б) а(х) = хе
х
, (3(х) = х;
1-созх
в) а(х) = , р(х) = х;
х
г) а(х) = е
2х
- е
х
, Р(х) = зіп 2х - зіп х.
7.131.
Довести, що нескінченно малі функції а(х) і Р(х)
одного порядку малості:
1-х /—
а) а(х) = , Р(х) = 1-Ух, х
—>
1;
1
+ х
б) а(х) =
1
- х, р(х) =
1
- л/х, х -> 1;
в) а(х) = л/4 -х -2, Р(х) = х, х
—>
0.
7.132. Порівняти нескінченно малі функції а(х) і р(х) при
х->0:
а) а(х) = X
і
зіп
2
х, Р(х) = х
1§
х ;
б) а(х) =
1п (1
+ Зх зіп х), Р(х) =
\%
х
1
;
в) а(х) = а
х
-1, р(х) = х1па.
7.133. Довести вказані рівності при х -> 0:
а) х
3
агсзіп
2
Зх = о(х
3
);
б) 2х
2
+ хІ§х = о(х);
в) л/2 + х
3
-л/2 =0(х
3
).

288
Глава 7. Границі та неперервність функцій
7.134. Визначити порядок малості нескінченно малої
функції а(х) відносно Р(х) = х при х -» 0 :
а) а(х) = х
3
+ 100х
2
; б) а(х) = *
(х + гХ
) ;
1
+ л/х
7х
10
в) а(х) = л/х
2
- л/х ; г) а(х) =
х
3
+1
д) а(х) = л/і + хзіпх -1; е) а(х) = л/зіп2х ;
є) а(х)=
ЗVx
3
1-х
§2.
Неперервність функцій
І. Короткі теоретичні відомості
Означення неперервності. Функція /(х) називається неперервною
в точці х = а, якщо:
1) функція /{х) визначена в точці х = а і деякому її околі;
2) існує скінченна границя Ііт /(х);
3) ця границя дорівнює значенню функції в точці х = а , тобто
Ній/(*) = До). (7-12)
З умови неперервності (7.12) випливає, що
Ііт /(х) = /(Птх), (7.13)
Х—ЇА Х—ЇА
що дає правило граничного переходу під знаком неперервної функції.
Умова неперервності (7.12) може бути також представлена у вигляді
Нт ДДа) = 0 (7.14)
&Х->0
або у вигляді
/(а + 0) = Да~0) = /(а). (7.15)
Умова (7.14) означає, що для неперервної в точці х = а функції, не-
скінченно малому приросту аргументу в точці а відповідає , нескінченно
мале значення приросту функції в цій точці.

§2.
\\е\\ерсрау\\сть фуцкщй
Умова (7.15) означає, що для неперервної в точці х -• а функції, гра-
ниця функції справа в точці а дорівнює границі функції зліва в точці а і
дорівнює значенню функції в цій точці.
Якщо функція неперервна в кожній точці деякої області, то вона нази-
вається неперервною в цій обметі.
Точки розриву. Точка а , в якій порушена хоча б одна з умов непе-
рервності, називається точкою розриву функції
/(яг).
Точки розриву класифікуються таким чином.
Якщо існують скінченні границі /(а + 0) і /(а -0), причому не всі
три числа /(о + 0), /(а-0), /(о) рівні між собою, то точка а називається
точкою розриву першого роду.
До точок розриву першого роду відносяться точкиуеувного розриву та
точки розриву типу "стрибок".
Якщо
Да + 0) = /(а-0)*/(а), (7.16)
то точка х = а називається точкою усувного розриву.
Якщо
/(в+0)*/(я-0), (7.17)
то точка х = а називається точкою "стрибка ",
а величина
Д/=/(а + 0)-/(в-0) (7.18)
стрибком функції /(х) в точці а .
Точка а називається точкою розриву другого роду функції /(х) , якщо
хоча б одна з границь /(а
+
0), /(а-0) не існує або дорівнює нескінченності.
Властивості неперервних функцій
Арифметичні операції над неперервними функціями. Нехай функції
/(.*) та ф(х) неперервні в точці х=а. Тоді в цій точці неперервні функції:
с
•/(*),
с =
соп8І;
Дх)±
Ф
(х); Дх)-ф(х); Ц^- (<р(а)*0).
ф(х)
Неперервність складної
функції.
Якщо функція х =
ц>(()
неперервна в
точці а, а функція у- /(х) неперервна в точці Ь = ф(й), то складна функ-
ція у =
/[($>(()]
неперервна в точці а .
Неперервність оберненої
функції.
Нехай функція у = /(х) визначе-
на, зростаюча (спадна) і неперервна на відрізку [а,Ь], де {(а)-а,
/(Ь) -
(3
(а < Р). Тоді ця функція має на відрізку [а.Ь] обернену функцію
х = /''(у) або х ф(г), яка є зростаючою (спадною) і неперервною.

290
Глава
7.
Границі
та
неперервність функцій
Неперервність елементарних функцій. Елементарні функції непе-
рервні
в
усіх точках,
в
яких вони визначені.
Властивості функцій, неперервних
на
відрізку
Функція
Дх)
неперервна
на
відрізку [а,Ь], якщо вона неперервна
в
кожній точці відрізка, причому неперервність
в
точці
а
означає непе-
рервність справа, тобто
Да
+
0)
=
/(а), а
неперервність
в
точці
Ь
означає
неперервність зліва, тобто /(6-0)
= ДЬ).
Функція
/(х),
неперервна
на
відрізку [а,Ь],
має
такі властивості:
1) обмежена
на
відрізку [а,Ь];
2) досягає
на
відрізку
[а,
Ь]
свого найбільшого
та
найменшого значення;
3) приймає
всі
проміжні значення
між Да) = А\ /(Ь) =
В,
АФВ,
тоб-
то
для
будь-якого числа
С , що
лежить
між
числами
А і В,
знайдеться така
точка
с є
(а,Ь),
що Де)
=
С ;
4)
за
умови,
що Да)
•
ДЬ) < 0 ,
існує хоча
б
одна точка се(а,Ь) така,
що
Де) = 0
Рівномірна неперервність. Функція
Дх)
називається рівномірно
не-
перервною
на
проміжку
X,
якщо
для
будь-якого
є > 0
знайдеться таке
5
= 5(є) , що для
будь-яких
х', х" є X з
нерівності |
х -
х"|
< 8
випливає,
Що
|ДдО-/(*')|<є.
Теорема Кантора. Якщо функція
Дх)
неперервна
на
відрізку [а,Ь],
то вона рівномірно неперервна
на
ньому.
//. Контрольні питання
та
завдання
1. Дайте означення функції, неперервної
в
точці.
2.
Дайте означення точки розриву функції. Наведіть класи-
фікацію точок розриву функції.
3.
За
яких умов складна функція неперервна; обернена функ-
ція неперервна?
4.
Сформулюйте поняття неперервності функції
на
відрізку.
5.
Наведіть властивості функцій, неперервних
на
відрізку.
6. Дайте означення рівномірно неперервної
на
проміжку
функції.
