Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1

Подождите немного. Документ загружается.

§2.

Застосування

диференціального

числення

331

Приклад 2. Написати рівняння дотичної і нормалі до па-

раболи у =

у[х

у точці з абсцисою х - 4.

• Знаходимо похідну функції у = Гх:

2л[х'

Звідси кутовий коефіцієнт дотичної к = у'(4) = — . Оскільки точка до-

тику має координати х = 4, у = 2 , то рівняння дотичної є:

у-2

= —(х-4) або х-4^ + 4 = 0.

В силу умови перпендикулярності кутовий коефіцієнт нормалі Аг, =-4.

Звідси рівняння нормалі має вигляд:

-2 = ~4(х-4) або 4х

у-\& = 0 . -4

Приклад 3. Скласти рівняння дотичної та нормалі до кри-

вої X

+ 2.ту

+ Зу

- 6 у точці .

• 3 рівняння кривої X

+ 2ху

Зу

= 6 знаходимо похідну у':

2х

2у

4хуу'+12у

у' = 0,

у'-

Звідси

у'\

(иі

2ху

6у

+ (-1)

"°

2-1-(-1)

+ 6-(-1)

Рівняння дотичної:

+ 1=—(х-1) або х-4у-5 = 0.

Рівняння нормалі:

= -4(х-1) або 4х + у-3 = 0.<

Приклад 4. Знайти кут між параболами у - 8 - х та

у = X

332

Глава 8. Диференціальне числення функцій однієї змінної

• Розв'язуємо сумісно рівняння парабол:

у =

—

=> 8-х

= х

=> 2х

=8 => X

=4 => х = ±2 .

У = х

Тоді у = 4.

Отже, маємо дві точки перетину парабол А(2,4), £(-2,4).

Продиференціюємо рівняння парабол:

з рівняння у = 8 - х

маємо у' = -2х , з рівняння у = х

маємо у' = 2х .

Знайдемо кутові коефіцієнти дотичних до парабол у точці А(2,4):

*,=(-2д0|,

=-4, к

=(2х)\

х=2

=4.

Отже,

4 + 4 8

Ф, = агсі£

Аналогічно, визначається кут між кривими в точці В(-2,4):

*, ={~2х)\

= 4,к

=(2х)|

ї=

=-4.

-4-4 8

8 ^

Фг =агсі8—

Приклад 5. Залежність шляху від часу при прямолінійному

2 . пі ,

русі точки задана рівнянням з = —і—зіп— (і - у секундах,

5 я 8

5-у

метрах). Визначити швидкість руху в кінці другої секунди.

• Знаходимо похідну від шляху по часу. Отримуємо швидкість руху:

сіп 4 1 пі

V- — =

н—соз—.

сії 4 8

-При

= 2 маємо у\ , = 16н л/2 я 16,18

І/=2 §

Отже, швидкість руху в кінці другої секунди у ~ 16,18 м/с. А

Приклад 6. По параболі у

х(8-х)

рухається точка так,

що її абсциса змінюється в залежності від часу / за законом

= 141 ((-у секундах, х - у метрах). Яка швидкість зміни орди-

нати у точці М(],7)?

§2.

Застосування диференціального числення

333

• Знайдемо закон зміни ординати, поклавши х =

1\Гі

у рівнянні пара-

боли у = х(8-х). Отримаємо у =

8іт[ї

-I

. Швидкість зміни ординати є

похідна від ординати по часу: у'= \2л[ї - Зі

. Для точки М(1,7) значення

Отже, у'

= 9, тобто швидкість зміни ординати дорівнює 9 м/с. Ч

Теореми про диференційовні функції

Приклад 7. Показати, що задана функція Дх) задо-

вольняє умовам теореми Ролля на [а, Ь]. Знайти відповідне зна-

чення с є (а, Ь), таке, що /'(с) - 0 .

а) /(х) = х

- 6х + 100; а = 1, Ь = 5;

б) Дх) = л/8х-х

; а = 0, Ь = 8 .

• а) функція /(х) = х

-6х+100 неперервна на відрізку

[1,5];

/'(х) = 2х-6, отже, функція диференційовна на інтервалі (1,5);

/(1) = /(5) = 95. Умови теореми Ролля виконані.

Для знаходження с є

(1,

5), такого, що /'(с) = 0, розв'язуємо рівняння:

/'(*) = 2х-6 = 0,

х = 3.

Отже, с = х = 3 .

б) функція Дх) = л/8х -х

неперервна на відрізку [0, 8]; похідна

—

2х

) = = існує для х

0, х * 8 , тобто на інтервалі (0, 8) ;

3-^(8х-х

)

/(0) = /(8) = 0 . Умови теореми Ролля виконуються.

Для знаходження с, розв'язуємо рівняння:

/'(*) = —*^= = 0,

3-^(8х-х

)

і-2х = 0.

х = 4.

Отже, с = х-А Л

334

Глава 8. Диференціальне числення функцій однієї змінної

Приклад 8. Чи виконуються умови теореми Ролля для та-

ких функцій:

5-х

а) /(х) = —т— на відрізку [-1,1];

б) Дх) = ^(х-8)

на відрізку [0,16]?

5-х

• а) для функції /(х) = —-— порушена умова неперервності функції

на відрізку [-1,1]. Точка х = 0 є

[-1,1]

є точкою розриву функції.

б) для функції Дх) = д/(х - 8)

порушена умова диференційовності

функції на інтервалі (0,16).

Дійсно, /'(х) = , у точці х = 8є(0,16) не існує. А

З-л/х-8

Приклад 9. Показати, що похідна многочлена

/(х) = х

- х

-х +

має дійсний корінь в інтервалі

(-1,1)

• Функція /(х) задовольняє умовам теореми Ролля (вона неперерв-

на на [-1,1], диференційовна на (-1,1), /(-1) = /(0 = 0). Отже, існує така

точка с є (-1,1), що У'(с) = 0 , тобто існує хоча б один дійсний корінь рівнян-

ня /'(х) = 0 . Знайдемо цей корінь, розв'язавши рівняння:

/'(х) = 3х

-2х-1=0.

Корені цього рівняння х, = -1, х

= 1; х, = с = -1 є (-1, 1). -4

Приклад 10. Перевірити виконання умов теореми Лагран-

жа для функції Дх) = х-х

на відрізку

[-2,1]

і знайти

відповідне проміжне значення с.

• Функція /(х) = х-х

неперервна на відрізку [-2,1];

) -

~ Зх

, отже, функція диференційовна на інтервалі (-2, 1). Умови

теореми Лагранжа виконані, отже, існує таке с є (-2,1), що

Д1)-Д-2) = /»П-(-2));

0-6 =

/'(с)-3;

ЛО = -2.

§2.

Застосування диференціального числення

335

Враховуючи вираз для

/'(х),

маємо:

- Зс

= -2 => Зс

= 3 => с

Шукане с =

-1,

бо -1 є (-2, 1). -4

Приклад

11.

На дузі АВ кривої /(х) = 2х - х

знайти точку

М , в якій дотична паралельна хорді АВ, якщо А(1, 1), В(3,-3).

• Функція /(де) = 2х - х

неперервна та диференційовна при всіх зна-

ченнях х , а значить і на відрізку [1, 3]. Згідно з теоремою Лагранжа існує

така точка с є

(1,

3), що виконується рівність:

Л3)-/(1) = /'(с)(3-1),

де /'(х) = 2-2х .

Підставивши відповідне значення, маємо:

(2-3-3

)-(2-1-1

) = (2-2с)-2,

-4 = 4(1-с),

1-с =

-1,

с = 2.

Тоді /(2) = 0 . Отже, шукана точка М(2,0). ^

Розкриття невизначеностей за правилом Лопіталя

Приклад 12. Показати, що правило Лопіталя не може бути

використане для обчислення вказаної границі:

х + зіпх

Ііт

.Ї-»ОО

х + СОЗ X

Обчислити цю границю, не використовуючи правила Лопі-

таля.

• Чисельник і знаменник даного дробу неперервні, диференційовні та

прямують до нескінченності. Знайдемо границю відношення похідних:

(Х + 5ІПХ)' ,. 1 + С05Х

Ііт = Ііт

(х

СОЯХ)' *->°°1—зіпх

Ця границя не існує, бо, враховуючи, що | созх| < 1, |зіпх| <

, чи-

сельник (знаменник) приймають значення, що належать відрізку

[0,2],

а саме

відношення похідних приймає будь-які невід'ємні значення.

336

Глава 8. Диференціальне числення функцій однієї змінної

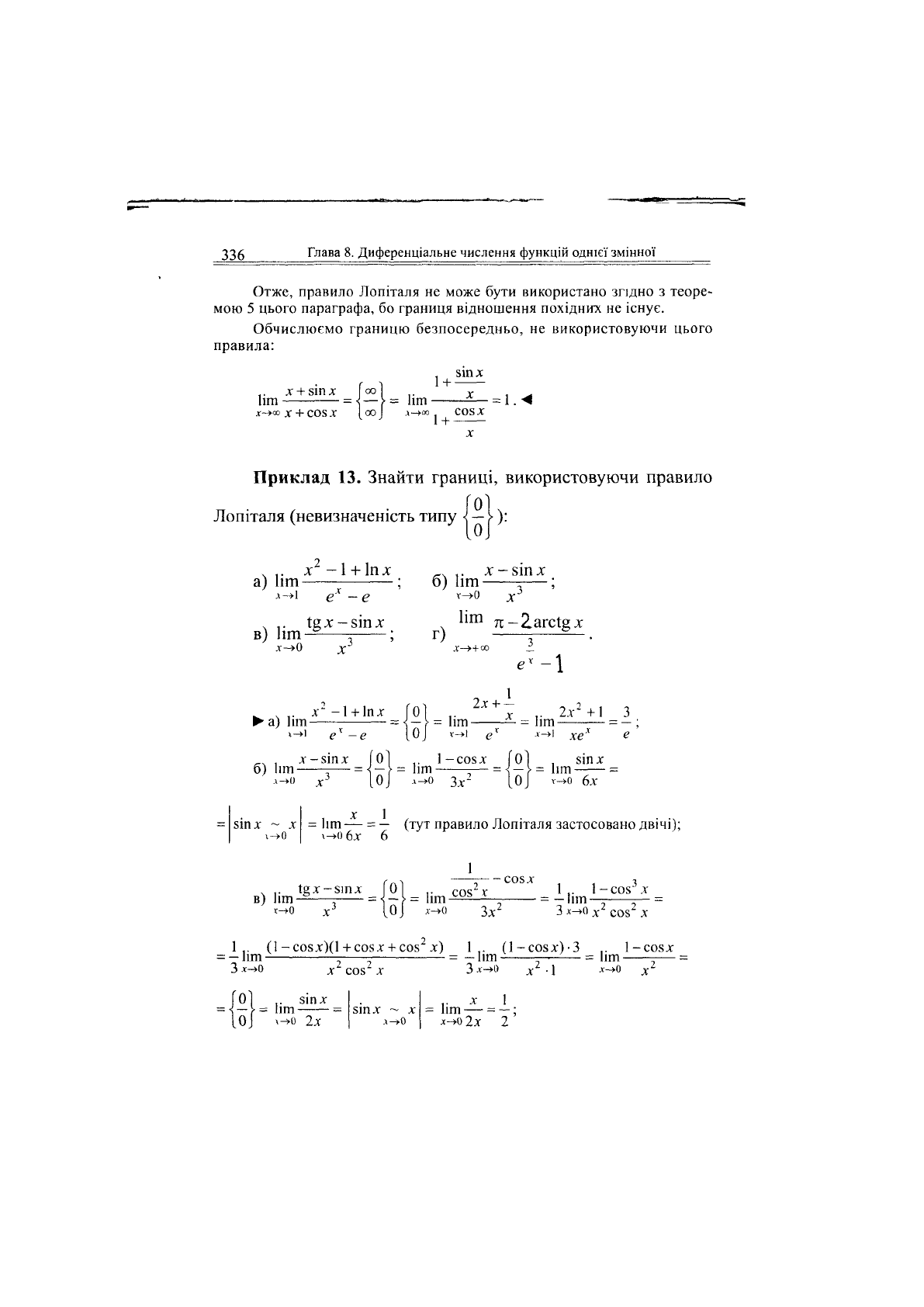
Отже, правило Лопіталя не може бути використано згідно з теоре-

мою 5 цього параграфа, бо границя відношення похідних не існує.

Обчислюємо границю безпосередньо, не використовуючи цього

правила:

ЗІПХ

1 +

+ 81ПХ оо

Ьт = і —} = Ііт — = 1. -4

дг~>°°

X + СОЗ X І ОО |

л->оо

С08Х

Приклад

13. Знайти границі, використовуючи правило

Лопіталя

(невизначеність типу | Ц

1):

,. х -1 + Іпх

а)

пт :

-е

І2

—

8ІП

в)

Ііт-

г ;

б)

Ііт

Х-81ПХ

г->0

г)

пт

тг-2.агс1:§х

з"

-1

•

а) 1іт

б) Ііт

-Є

Х-81ПХ

,„-, 2х +

—

+ 1пх 0 ,.

-> = Ііт -

х"

2х

+1 З

1-СОЗХ

Ііт — = \

—

\ = Ііт

•>->» Зх

І01 *->о 6х

хе

8ІПХ

81ПХ

~ X

»->0

= Ііт — =

—

(тут правило Лопіталя застосовано двічі);

і->о

6х 6

в)

Ііт

г§

х -

81П

х 10

пт

созх з

соз х 1 .• і - соз х

^оз £ __ _|

іт

0] *-><> Зх

Зх^о

соз

1,. (1-созх)(1 + созх + соз х) 1,. (І-созх)-З ,.

1-С08Х

= —Ііт

;

^ =

—

Ііт -—= Ііт —

З х->0

[0І

«!!£

0 2х

соз

51ПХ

~ X

л->0

З *-Ю х

•

х->0

Ііт

х-*й

їх 2

§2.

Застосування диференціального числення

337

г)

ьт

7І

аГСЄ§Х

(°1

= Ііт

_1±*і=

Нт

-1 е

оо 2 ,. 2х 2 .

— >=

—

Ііт — =

—

со І

г-»+°°

2х З

Приклад 14. Знайти границі, використовуючи правило

оо і

Лопіталя (невизначеність типу

— Н

со

а) Ііт ^

ПХ

; б) Ііт

г->0 СІ§Х

1п

х х!п(х-5)

в) Ііт

*-»5

1п(е* - Є

)

• а) Ііт

ІП

І оо

—

= Ігт-

Ііт

зіп х 10

->0СІ§Х

[оо] х->0 1 х->0 х

51П

зіпх ~ х

х->0

= - Ііт — = Ііт х = 0 ;

д:->0

X *-»0

б) Ііт

ІП

X 00

л:—>+оо

21пх-

— \= Ііт

2 , Іпх

[

оо

—

Ііт

І х-*+к> Зх

ї->+оо

х 2 .. 1

= - Ііт -~ = - Ііт —- = 0;

*->+<ю

Зх 3

Ї->+ОО

їх

х1п(х-5) [оо

в) Ііт

—•

= {— }=

Ііт

*->5 1п(е

- Є

)

х-5

5 Ііт

е -е

1-і = -у Ііт — = -уе

=5.-4

[О]

^5 1

338

Глава

Диференціальне

числення функцій однієї змінної

Приклад 15. Знайти границі, використовуючи правило

Лопіталя (невизначеність типу {0

•

оо

}):

ЯХ

а) Ііт х е

;

б) Ііт

8Іп(х-

1)1§—; в) Ііт х Іпх.

.ї-»+оо

х-+\ 2 х->+0

•

а) Ііт х

е " = {0-оо}=

і_

|*1=

ііт

3 1іт^= і" =6

1іт-1

= 0;

б)

1ітзіп(х

-1)1§—= {0-со}

зіп(х-І)

~ х-1

ї->1

• •

/ ях

1іт(х-1)г§—=

ДГ-+І

Ііт

^ —

=1іт-

Х-+1

ЯХ 0 ї->1

СІ8

2,. . т ях 2

— Ііт зіп

— = :

я«і

2 я

зіп

™" 2

в)

Ііт х

Іпх = {0-оо}= 1іт^і={—1= Ііт

.т-> + 0 дг-> + 0

1 оо

лг-» + 0

- Ііт х

=0. ««

д~>+о

Приклад 16. Знайти границі, використовуючи правило

Лопіталя (невизначеність типу

{оо

оо}):

а) Ііт

х->0

1 1

V81п

X X )

(

X я

б) Ііт

_>1^с1§х

2 созх

•

а) Ііт

-Дг І = {со-со}= Ііт

*-><\зіп

х х )

(2 • 1 \

-зіп X

„:_2

2-2 4

ЗІП X ~ X

.г->0

х -зіп'х [0| .. 2х-зіп2х

Ііт =

—

>= Ііт ;

*->о

0 І ДГ->0 4Х

§2.

Застосування диференціального числення

339

1,. 2-со82х-2 1,.

1-со82х

0] 1,. 2$'т2х

—

Ііт = =

—

Ііт ={

—

}=—

Ііт

4*->о ЗЇ

6д-->о

[01

6*->о

2Х

8Іп2х

~ 2х

б)

Ііт

1 ,. 2х 1

— Ііт—

—

6->-»0

д- 3

_>"чСІ§д-

2С08Х

= {оо

—

оо}=

іт

Х-81ПХ

С08Х 2С08Х

2Х8ІПХ-Л

(0) ,.

28ІПХ+2ХС08Х

, .

= Ііт і

іт

-1.

-4

._,л

2С08Х

[0]

2(-8Іпх)

Приклад 17. Знайти границі, використовуючи правило

Лопіталя (невизначеності типу

{і°°},

{

со

°},

а)

1іт(со8

2х)

ї2

; б) 1іт(і§х)

2со8ї

; в) 1ітл:

1п(еГ

І)

х->0

, я *_>()

•

а)

1іт(со8

2х)

Скористаємось співвідношенням:

А з

—^

2 —^-ІПСО$2дг

(С082Х)'"

= Е

НТ2

)Х

Тоді

1іт(со82х)

=І1 |= Ііт є"

л-->о

;

.<•-><)

ІПС052.Х

1 , ,.

ІПС082Х

1іі"

ІПС082Х

„

Тут позначено Л = Нт . Знайдемо цю границю, застосовую-

д->0

чи правило Лопіталя:

ІПС082Х

0 ,.

С082Х

= Ііт =

- \ = Ііт

[0] д->о 2х

...

-2х

= 2 Ііт = -2 .

*г>о 2х

(-8Іп2х)-2

8Іп

2х ~ 2х,

ї->0;

С082х

-» 1,

д-->0.

340

Глава 8. Диференціальне числення функцій однієї змінної

Отже, 1ігл(соз2х)

г2

= е

3 ( 2)

=е

х->0

б) 1іт(1

х)

2со

Враховуючи, що {Щх)

2со

™"

"**

, маємо

л 1

1іт(і

х)

2со

=(оо°}= 1іт

2со5,ГІп,8дг

= {е

0со

)= е

2т

2 А

Є ,

1 1

,. ІПІ£Х [оо] І£Х СОВ

X .. 1

де Л = Ііт —^— = і

—

= Ьт --= Ііт

1 ^

^ — (-51ПХ) ^

СОЗХ С05 X

= Ііт созх = 0 .

х->—

Отже, 1іт(1

х)

2со,г

=е° = 1.

х->—

1 1 , , Іпх

- Іпх пт -

в) Нтх

"^-

* = (о°}= Ііте

"^-

' =

е'^''-

= е

х->0 л->0

, ,. Іпх ,.

.. е

-\ ,. е*-1 10

де А = Ііт = Ііт — = Ііт = Ііт =

< —

*->о Іп(е* -1) *->°

(

*->° х [0]

Ііт — = 1.

х->0 1

Отже, \ітх

1п(еХ

=е.<

х->0