Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§2.
Застосування диференціального числення 34]
Формула Тейлора
Приклад
18. Розкласти многочлен Р(х)=х
3
-2х
2
+Зх+5 за
степенями
двочлена (х - 2).
•
Знаходимо похідні многочлена та їх значення в точці х = 2 :
Р'(х) = 3х
2
-4х +
3;
Р"(х) = 6х-4; Р
я
(х) = 6 ; Р
іп)
(х) = 0 при п > 4 .
Р{2) = 11; Р'(2) = 7 ; Р"(2) = 8; Р
т
(2) = 6 .
Отже, за формулою Тейлора маємо:
х
3
-2х
2
4-3x4-5
=11 + 7(х-2) +
— (х-2)
2
4-—
(х-2)
3
2!
З!
або
х
3
-2х
2
4-3x4-5
=1І4-7(х-2)4-4(х-2)
2
4-(х-2)
3
.
Ч
Приклад
19. Розкласти функцію /(х) = 1§х за формулою
-і
Маклорена
до члена, що містить х включно.
•
Знаходимо похідні функції /(х) =
1§
х до третього порядку включ-
но,
а також їх значення при х = 0 .
Маємо
Дх) = Щх, Д0) = 0;
/'(*)
= —у- = соз-
2
х, /'(0) = 1;
С08
X
/"(х)
=
(-2)со8
_3
х
(-зіпх) = 2соз~
3
х-зіпх , /"(0) = 0;
/"(Х)
=
6С05"
4
Х-8ІП
2
Х
4-2с08"
2
Х,
/"(0) = 2 .
За формулою Маклорена з залишковим членом у формі Пеано маємо
х
3
Г2Х
= Х4- +
0(х
3
)
.
з
Або враховуючи, що
/"
(4)
(х)
=
6(4С08~
5
Х -8ІП
3
X 4-С08~
4
X
-
2
8ІП X
•
С08х)
4-
2
(-2)С08~
3
Х
•
(-8ІП
х) ,
/'
4)
(0) = 0, залишковий член можна записати у вигляді
о(х
4
),
тобто маємо
х
3
І£ X
= X
4- 4- О (X
4
) . Ч

342
Глава 8. Диференціальне числення функцій однієї змінної
Приклад 20. Розкласти функцію /(х) = Ух за формулою
Тейлора з центром розкладу у точці а =
1
(за степенями (х -1))
до члена з (х -1)
3
включно.
І
• Обчислимо значення функції /(х) = х
3
та її похідних до третього
порядку включно при х = а = 1.
12 5 8
Дх)
= я-з; Г(х)
=
V
3
;
/"(х) =
-|х"з;
/"(х)
=
Щх~*.
ЛІ) = 1; /'(1) = і; /"(О = -|; /"(1) = ^
•
Отже, за формулою Тейлора маємо:
VI = 1+ —(х-1) — (х-1)
2
+ -^-(х-1)
3
+о((х-1)
3
).<«
З 9-2! 27-3!
Приклад 21. Обчислити з точністю до 10
_3
наближене зна-
чення УЇ9
• Представимо заданий корінь у вигляді:
і
2 "із
^29 = ХІ21 + 2 = 3
1
+
V 27
Скористаємось біноміальним розкладом:
ч
,„ , т т(т-Х) •> т(т-\)...(т~п + \) „
(1
+ х) =1 + —
х+—
-х +... + — -— -х"
+
/?„.
1! 2! я!
Звідси маємо наближену рівність
п , \" л.
т
^{т-\) 2^ , т(т-\)...(т-п + \) „
(1
+ х) «1 + —Х + X +... + X ,
1!
2! я!
похибка якої
=
т(т-1)...(т-
Я
)
+
, _,
(я + 1)!
може бути зроблена як завгодно малою при Іх| <
1
та достатньо ве-
ликому я .

§2.
Застосування диференціального числення
343
Поклавши
х
~2~^ '
т
от
Р
имаємо
^29=311 +
_2_>з"
27
,
2 2
1
+ - +
2
3
-5 2
5
-5
1 81
2
3-81
3
3
•
81
4
Оцінюючи величини послідовних похибок обчислення ЗІ К
п
І, знаходимо
2 З
ЗІЛ||<3-^
Т
<0,002 ; ЗІ К
2
\<^—^-< 0,00007.
81
1 1
81
3
Отже, для обчислення з заданою точністю достатньо взяти три члени,
які передують залишку К
2
, тобто
29 =3(1 + 0,024 - 0,0006) = 3,072 . Ч
Приклад 22. Використовуючи розклади функцій за фор-
мулою Тейлора (Маклорена), обчислити задані границі:
... 1-соз х
а) Ііт—г г-
5х
2
+ 7х
3
б) Ііт
(х-1)-8Іп2(х-1)
*->1
(Х~1) +
8ІПЗ(Х-1)
в) Ііт
1§
X + 2 8ІП х - Зх
• а) Ііт
1
- соз х
«5х
2
+7х
3
5х
2
+ 7х
3
5х'
д-->0
,. (1-созх)(1 +созх + соз х) ,. З(І-созх)
= Ііт -=1іт
—
і->0
5*'
І
і х з
;со5х = 1 + о(х )
і 2!
*->° 5х
2
2 2
1-1+- о(х
3
) о(х
3
)
З 2' 3 2
і
=
—
Ііт г = — Ііт
-
5 д--»о
.2

344
Глава 8. Диференціальне числення функцій однієї змінної
б) Ііт
(х-1)-5Іп2(х-1) _
х->\
(х-1) +
8ІпЗ(х-1)
ЗІП
2(х -
1)
= + о(х - 1)
1!
зіп 3(х -1) =
3
(*~
П
+
0
(х -1)
1!
= Нт
.
(х-1)-2(х-1)-о(х-1) ,. -(х-1) 1
'"і-
- - =
Ьт —
- = —
(х
-1) +
3(х
-1) +
о(х
-1)
д-и4(х-1) 4'
.
,. іех + 2зіпх-3х
в) пт
•
*->о
х + —+ о(х
4
) + 2
З
Щх = х + —+ о(х
4
)
X
і
зіп х = х + о(х
4
)
6
(
г
3
х
/ 4
ч
х но(х )
6
-Зх
:
Ііт-
х->0
х
4
*-*о х
ч
Дослідження функцій та побудова графіків
Приклад 23. Дослідити функцію /(х) - ^
Х +
^ та побу-
х - 2
дувати її графік.
•
1. Область визначення функції £>(/) =
(-со,2)ІІ(2,
+
оо).
На інтер-
валі
(-оо,
2) Дх) < 0 , на інтервалі
(2,
+
оо)
/(х)>0.
2.
Функція не є парною, не є непарною, бо
Д-х)
=
(-х + 1)
2
(-х + 1)
2
-
х
- 2
х +
2
тобто Д-х) * Дх), Д-х)
*-Дх).
Функція неперіодична, бо не існує такого числа Т, Т > 0 , щоб
Дх + Т) = Дх), Ух є
/>(/).
Отже, маємо функцію загального вигляду.
3.
Точки перетину з осями координат
(-1,0)
та ^>
-
^
•
4.
Точка розриву функції х = 2 . Маємо розрив другого роду, бо
Ііт
/(х)
= -оо, Ііт
/(я)
= +оо.
<-->2-0
х->2+0

§2.
Застосування диференціального числення
345
5.
Вертикальна асимптота х = 2 , бо Ііт /(х) =
оо.
г->2
Похилі асимптоти шукаємо у вигляді у = кх
+
Ь.
Дх)
к = Ііт
ЛГ->±00 X
1іт
і£±і>1
= ,;
*-»±» х(х - 2)
Ь= Ііт
[/(х)-Ах]
= Ііт
(х + 1)
2
1-
4Х + 1
/І
= Ііт = 4 .
д-->±а>
X —2
Отже, у = х
+
4 - похила асимптота.
6. Знаходимо точки екстремуму та визначаємо інтервали монотонності
функції.
2(х + 1)(х-2)-(х + 1)
2
х
2
-4х-5 (х + 1)(х-5)
(х-2Г (х-2)" (х-2Г
Для знаходження критичних точок розв'язуємо рівняння /'(х) = 0 ,
тобто (х + 1)(х -5) = 0, (х-2)
2
Ф
0 , звідки х, = -1 , х
2
= 5 .
Критичні точки
X]
=
-1,
х
2
= 5 та точка х = 2 (це точка розриву функції)
поділяють область визначення функції на інтервали, які вказані на наведеній ниж-
че
схемі.
На цій схемі над віссю Ох вказано знак похідної функції у' = /
'(х),
під
віссю Ох показана поведінка функції у = /(х) на вказаних інтервалах. Тут
стрілками , X вказується відповідно, що функція зростає чи спадає. Слова
тах, тіп вказують відповідно точки, де функція досягає максимуму чи мінімуму.
знак у
поведінка
функції у
-1 0
тах \^
5
\^ тіп
/
2
точка
розриву
Отже, у
тт
= у{-\) = 0, у
тт
= у(5) = 12 .
На проміжку
(~оо,-1)и(5,
+
со)
функція зростає;
на проміжку
(-1,2)
СІ
(2,5) функція спадає.
7.
Знаходимо точки перегину графіка кривої та визначаємо інтервали
опуклості та вгнутості
'х
2
-4х-5
Л
(х-2У
Г(Х)ФО;
(2х-4)(х-2)~ -(х
2
-4х-5)2(х-2) 18
(х-2)
4
"(х-2)
3

346
Глава
8.
Диференціальне числення функцій однієї змінної
/"(х) < 0 на проміжку
(-со,2),
тобто крива опукла на цьому про-
міжку;
/"(х) > 0 на проміжку
(2,
+
оо),
тобто крива вгнута на цьому проміжку.
Точок перегину немає, бо точка х = 2 , в околі якої змінюється знак
другої похідної, є точкою розриву функції. Результати цього дослідження
наведено на схемі.
знак у"
поведінка 0 2 х
функції у О точка ^
Тут знак О означає опуклість, знак ^ - вгнутість.
8. Проводимо додаткові дослідження:
а) на інтервалі
(-оо,2)
/(х)<0 (графік нижче осі Ох), на інтервалі
(2,
+
оо)
/(х) > 0 (графік вище осі Ох);
б) дослідимо поведінку функції на нескінченності:
На основі дослідження поступово будуємо графік функції
розриву
Ііт /Хх) = Ііт
лг-> + сс X —2
.. (х + 1)
2
Ііт
->±°° х-2
= ±оо .
(* + 1)
х-2
2
/(*) =
, який наведено на рис.8.4.
Рис.8.4 <

§2.
Застосування диференціального числення
347
_х±
Приклад 24. Дослідити функцію
/(х)
=
хе
2
та
побуду-
вати
її
графік.
• 1. Область визначення функції £>(/)
= (-<»,+оо).
(-Д-)
2
х
2
2.
Функція
с
непарною, бо
/(-х)
=
-хе
2
=-хе
2
=-/(х), отже,
її
графік симетричний відносно початку координат.
Функція неперіодична,
бо не
існує такого числа
Т, Т > 0 ,
щоб
Дх
+
Т)
=
/(х), Ух є
/)(/).
Отже, маємо функцію загального вигляду.
3.
Точка перетину графіка функції
з
осями координат (0,0).
4.
Точок розриву функція
не
має.
5.
Вертикальних асимптот функція не має,
бо
не існує такого числа
а ,
щоб
Ііт
/(х)
= оо .
х—>а
Похилі асимптоти шукаємо
у
вигляді
у
=
кх
+
Ь.
_х±
к
= Ііт №- = Ііт
Іі-І-
= Ііт -4г = 0 ;
*-»+<*>
х дг-»±« х
х->±<»
е
х
/2
2
Ь=
Ііт
[/(х)-кх]=
Ііт хе
2
= Ііт
—\-г-=
і
—
1=
Нт
—г-|
= 0
*->±°о дг->±<х>
Ї->±ОО
^х /2 [оо]
л--»±а>
х /2
_
х
Отже, маємо горизонтальну асимптоту
у
=
0.
6. Досліджуємо функцію
на
екстремум
та
знаходимо інтервали моно-
тонності.
ґ
-2 \ ,2 2
е
2
+хе'
2
-(-х)=е~
2
(1-х
2
)
1 Х
V ^
е
е
2
/2
х
2
/2
'
/'(х)
= 0; і-^- = 0;
1-х
2
=0;
х,=-1,х
2
=1.
Отримали критичні точки,
які
розбивають числову вісь
на
три інтер-
вали. Дослідження знаку першої похідної
на цих
інтервалах
та
висновки

348
Глава 8. Диференціальне числення функцій однієї змінної
відносно поведінки функції на них наведено на схемі.
знак у
поведінка
0 1
тах
функції у \^ тіп тах \^
На проміжку
(-оо,-1)и(1,
+
со)
функція спадає;
на проміжку (-1,1) функція зростає.
У
тт
=у(-1)
= -е
2
=—^-«-0,6; і>
тах
=у(\) = е
2
=-^«0,6.
Є ' Є'
7.
Досліджуємо функцію на опуклість, вгнутість та знаходимо точки
перегину.
Ґ(х) =
ґ
\-х
2
^
-2хе
х2/2
-(\~х
2
)е^
2
_ хе
х2
І
2
{-2-\ + х
2
) _ х(х
2
-3)
е е
1
/\х) = 0; х(х
2
-3) = 0; х, = 0 , х
2
= -Уз , х
3
= Уз .
Отримали критичні точки другого роду, які розбивають числову вісь
на п'ять інтервалів.
знак у
поведінка -Уз 0 Уз х
функції у ГЛ точка ^ точка О точка ^
перегину перегину перегину
Функція опукла на проміжку (-оо,-Уз)
ЦІ
(0,Уз~),
бо /*(х)<0;
функція вгнута на проміжку
(-Уз,
0) У
(Уз,
+
оо),
бо /"(х) > 0.
Оскільки в околі точок х х = 0 у" змінює знак, то при цих
значеннях абсцис маємо точки перегину.
Підрахуємо значення функції в цих точках:
г Уз
Я±Уз)
= ±-^-*±0,4; у(0) = 0.
Маємо три точки перегину
Р[(-УЗ;-0,4),
/>
2
(УЗ;0,4),
Р
3
(0;0) .
§2.
Застосування диференціального числення
349
8. Проводимо додаткові дослідження:
а) на інтервалі
(-оо,0)
/(х) < 0 (графік нижче осі Ох), на інтервалі
(0,
+
со)
/(х)>0 (графік вище осі Ох);
б) дослідимо поведінку функції на нескінченності:
Ііт /(х)= Ііт хе
2
= Ііт —гу-
.т->±оо
і-->±оо
Л->±°0 X /2
= Ііт
ОО
і
д-->±со
е
х
і- ,х
= 0.
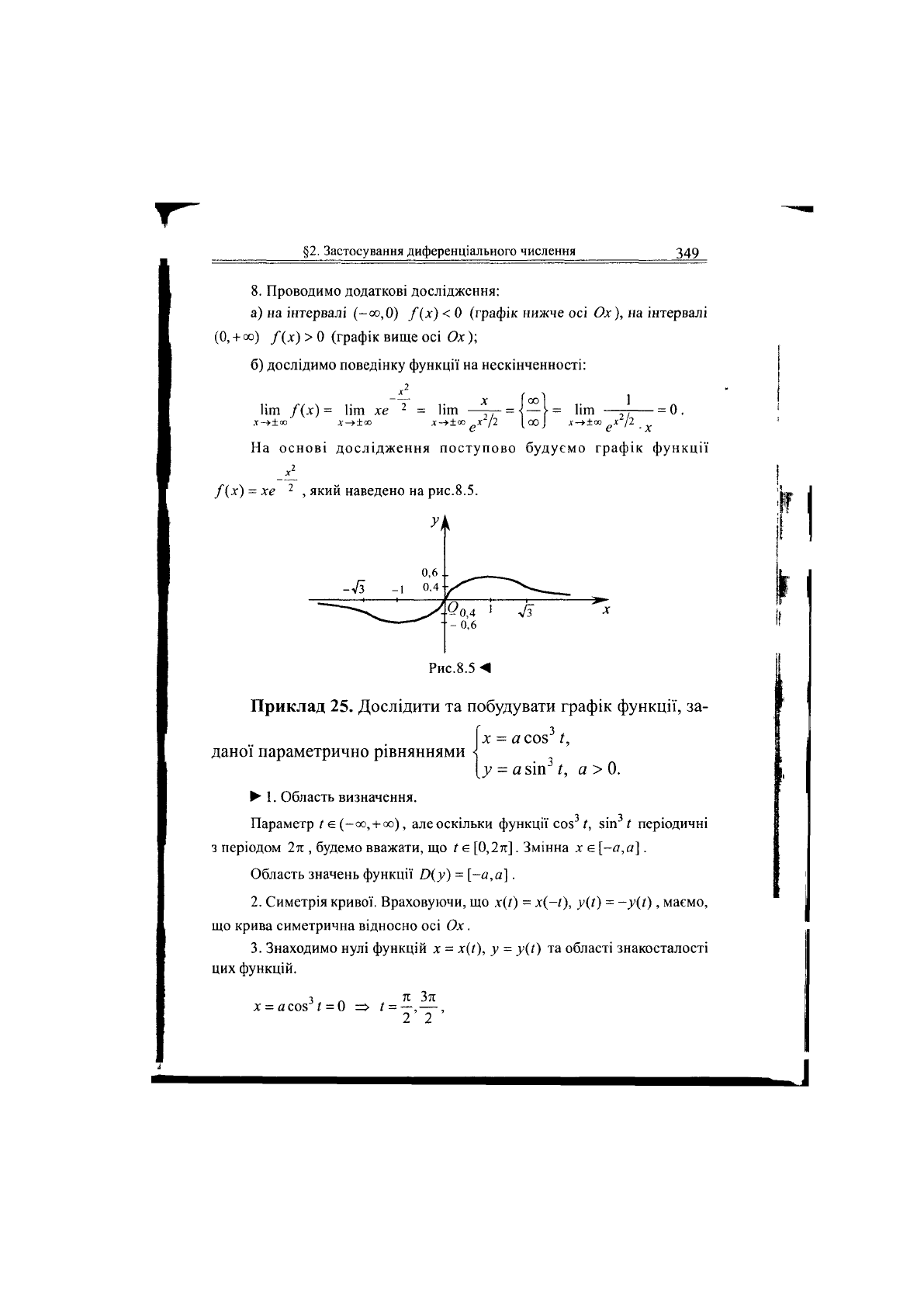
На основі дослідження поступово будуємо графік функції
_х±
/(х) = хе
2
, який наведено на рис.8.5.
Рис.8.5-4
Приклад 25. Дослідити та побудувати графік функції, за-
даної параметрично рівняннями
• 1. Область визначення.
| х = а соз і,
[у -
азіп
3
1,
а>0.
Параметр
:є(-оо,
+
оо),
але оскільки функції
соз
3
1,
зіп
3
/ періодичні
з періодом 2л , будемо вважати, що І є
[0,2л].
Змінна х є [-а,а].
Область значень функції £>(>>) =
[-а,а]
•
2.
Симетрія кривої. Враховуючи, що х(і) =
х(-і),
у(і) =
-у(і),
маємо,
що крива симетрична відносно осі Ох.
3.
Знаходимо нулі функцій х - х(і), у = у (і) та області знакосталості
цих функцій.
п Зл
х = а соз
1
=
0 =>
1
=
-
2 2

350
Глава 8. Диференціальне числення функцій однієї змінної
функція х(с) знакододатна на проміжку
0,^
2
II
Зл
2л
у = а зіп
3
і = 0 => / = 0, л,2л ,
функція у(() знакододатна на проміжку
[0,
я].
4.
Крива не має похилих асимптот, бо у є [-а,а].
5.
Знаходимо точки і
к
, в яких хоча б одна з похідних х\, у] дорівнює
нулю або розривна.
X
і
. - -Засох
2
; х, = -Засоз
2
г -
зіп / = 0 , / =
0,
—,—,2л .
2 2
у\
—
За зіп
2
1
-
соз/; у\ = За зіп
2
г-соз/ = 0,1 =
0,—,—,2я
.
Знаходимо :
а>
^1
х,
2 2
За зіп г-соз/
сіх ' " х\ -Засоз" / -зіп/
Далі складаємо таблицю, враховуючи отримані точки та значення похідних.
Область
зміни /
Відповідна
область
зміни X
Відповідна
область
зміни у
Знак
сіх
Характер зміни у
як функції від X
(У
=
/(*))
0</<*
2
а>х >0
0<у<а -
спадає
я
—
<
7
< я
2
0>х>-а
а>у>0 +
зростає
Зя
я < / < —
2
-а<х<0
0>у>-а -
спадає
— <
*
< 2л
2
0<х <а
-а<у<0 +
зростає
З таблиці видно, що задані параметричні рівняння визначають дві не-
перервні функції вигляду у =
/(х)
:
при 0 < І < я маємо у > 0 (два перші рядки таблиці);
при я < І < 2я маємо у < 0 (два останні рядки таблиці).
З виразу для похідної — = -Щі випливає, що
йх
.. сіу
о; Ііт — = +со .
,^1ісіх
ІіігД
.'сіх
2
2
У цих точках дотична до кривої вертикальна.
