Тиманюк В.А., Животова Е.Н. Биофизика

Подождите немного. Документ загружается.

251

â îðãàíèçìå N

= 10

, äëÿ êàïèëëÿðîâ óêàçàííûå âåëè÷èíû ðàâíû ñîîò-

âåòñòâåííî l

= 1 ìì, R

= 3 ìêì è N

= 10

. Ñðàâíèòå ïîëó÷åííûé îòâåò

ñ îòíîøåíèåì ñîïðîòèâëåíèÿ X

0 à

0 ê

åäèíè÷íîé àðòåðèîëû è åäèíè÷íî-

ãî êàïèëëÿðà.

Ðåøåíèå. Ãèäðàâëè÷åñêîå ñîïðîòèâëåíèå îäíîãî ñîñóäà ðàâíî

Ïðè ïàðàëëåëüíîì ñîåäèíåíèè N îäèíàêîâûõ ñîñóäîâ èõ îáùåå ñî-

ïðîòèâëåíèå ñîñòàâëÿåò:

èëè

Òîãäà îòíîøåíèå ñóììàðíûõ ãèäðàâëè÷åñêèõ ñîïðîòèâëåíèé àðòåðè-

îë è êàïèëëÿðîâ ðàâíî

акак

кака

XNl

XNlR







Ïîäñòàâèì ÷èñëåííûå äàííûå:

−−



⋅⋅



⋅⋅



10 2 6

83 6

10 10 3 10

10 10 15 10

1,6.

Îòíîøåíèå ãèäðàâëè÷åñêèõ ñîïðîòèâëåíèé åäèíè÷íûõ ñîñóäîâ ðàâíî

àê

êà

0а

0к

10 3 10 1

0, 016

62,5

10 15 10

XlR

−−



⋅

== ==



⋅



Òàêèì îáðàçîì, ñóììàðíîå ãèäðàâëè÷åñêîå ñîïðîòèâëåíèå àðòåðèîë

â 1,6 ðàçà ïðåâûøàåò ñóììàðíîå ñîïðîòèâëåíèå êàïèëëÿðíîé ñåòè, â òî

âðåìÿ êàê ñîïðîòèâëåíèå îäíîé àðòåðèîëû ïî÷òè â 63 ðàçà ìåíüøå ñî-

ïðîòèâëåíèÿ îäíîãî êàïèëëÿðà.

Çàäà÷à 8.3. Èññëåäîâàíèÿ ïîêàçàëè, ÷òî â ðåçóëüòàòå îòëîæåíèé õîëå-

ñòåðèíà â àîðòå ïàöèåíòà òîëùèíà åå ñòåíêè óâåëè÷èëàñü â 1,5 ðàçà, âíóò-

ðåííèé äèàìåòð óìåíüøèëñÿ íà 25 %, à ñêîðîñòü ðàñïðîñòðàíåíèÿ ïóëü-

ñîâîé âîëíû âîçðîñëà â 1,9 ðàçà. Êàê èçìåíèëñÿ ïðè ýòîì ìîäóëü óïðóãîñòè

ñòåíêè ïî îòíîøåíèþ ê íîðìå?

Ðåøåíèå. Ñêîðîñòü ðàñïðîñòðàíåíèÿ ïóëüñîâîé âîëíû îïðåäåëÿåòñÿ

ïî ôîðìóëå:

Ïðàêòè÷åñêèå è òåñòîâûå çàäàíèÿ

252

îòêóäà ìîæíî âûðàçèòü ìîäóëü óïðóãîñòè

Ó äàííîãî ïàöèåíòà òîëùèíà h àîðòû, åå âíóòðåííèé äèàìåòð d è ñêî-

ðîñòü v ðàñïðîñòðàíåíèÿ ïóëüñîâîé âîëíû â íîðìå è ïðè ïàòîëîãèè ñîîò-

íîñÿòñÿ ñëåäóþùèì îáðàçîì:

пн

= 1, 5hh;

пн

=d0,75d;

пн

1, 9vv= .

Òîãäà îòíîøåíèå êîýôôèöèåíòîâ óïðóãîñòè â íîðìå è ïðè ïàòîëîãèè

ñîñòàâèò:

пппн н нн

ннп нн н

d(1,9)0,75d

1, 8.

dd1,5

Evh v h

vh v h

⋅

== =

⋅

Òàêèì îáðàçîì, â ðåçóëüòàòå ðàçâèòèÿ àòåðîñêëåðîçà, êîýôôèöèåíò

óïðóãîñòè àîðòû óâåëè÷èëñÿ â 1,8 ðàçà.

ÇÀÄÀ×È ÄËß ÑÀÌÎÑÒÎßÒÅËÜÍÎÃÎ ÐÅØÅÍÈß

8.1. Âû÷èñëèòå âÿçêîñòü êðîâè η ïðè íîðìàëüíîì ãåìàòîêðèòå

(c = 45 %), åñëè âÿçêîñòü ïëàçìû ñîñòàâëÿåò η

= 2,0 ìÏà•ñ.

8.2. Âû÷èñëèòå ìàêñèìàëüíûé ìèíóòíûé îáúåì Q

max

êðîâè, ïðè êî-

òîðîì òå÷åíèå êðîâè â àîðòå îñòàåòñÿ ëàìèíàðíûì. Äèàìåòð àîðòû d = 2 ñì,

âÿçêîñòü êðîâè η = 5 ìÏà•ñ, ïëîòíîñòü ρ = 1050 êã/ì

, êðèòè÷åñêîå çíà-

÷åíèå ÷èñëà Ðåéíîëüäñà Re

êð

= 2000.

8.3. Ñðåäíÿÿ ñêîðîñòü êðîâîòîêà â àîðòå ñîñòàâëÿåò v

àîð

= 0,45 ì/ñ,

à â êàïèëëÿðàõ — v

êàï

= 0,5 ìì/ñ. Âî ñêîëüêî ðàç ïëîùàäü ïîïåðå÷íîãî

ñå÷åíèÿ àîðòû ìåíüøå ñóììû ïîïåðå÷íûõ ñå÷åíèé êàïèëëÿðîâ?

8.4. Âû÷èñëèòå ãèäðàâëè÷åñêîå ñîïðîòèâëåíèå X àîðòû, åñëè åå äèà-

ìåòð ñîñòàâëÿåò D = 2,4 ñì, äëèíà l = 40 ñì, âÿçêîñòü êðîâè η = 5 ìÏà•ñ.

8.5. Âû÷èñëèòå ñêîðîñòü v îñåäàíèÿ åäèíè÷íûõ ýðèòðîöèòîâ, ñ÷èòàÿ

èõ ñôåðè÷åñêèìè ÷àñòèöàìè äèàìåòðîì d = 7 ìêì. Âÿçêîñòü ïëàçìû ñî-

ñòàâëÿåò η = 2,2 ìÏà•ñ, ïëîòíîñòü ýðèòðîöèòîâ ρ

ýð

= 1080 êã/ì

, ïëîò-

íîñòü ïëàçìû ρ

ïë

= 1027 êã/ì

8.6. Â ðåçóëüòàòå ëàáîðàòîðíîãî èçìåðåíèÿ ÑÎÝ îêàçàëîñü ðàâíûì

v = 10 ìì/÷àñ. Èñïîëüçóÿ èñõîäíûå äàííûå çàäà÷è 8.5, âû÷èñëèòå ñðåä-

íåå ÷èñëî N ýðèòðîöèòîâ â àãðåãàòå, åñëè ñðåäíèé îáúåì åäèíè÷íîãî ýðèò-

ðîöèòà ðàâåí V

= 100 ìêì

8.7. Ñêîðîñòü ðàñïðîñòðàíåíèÿ ïóëüñîâîé âîëíû ïî àðòåðèè ñîñòàâ-

ëÿåò v = 10 ì/ñ. Îïðåäåëèòå ìîäóëü óïðóãîñòè E àðòåðèè, åñëè òîëùèíà

åå ñòåíêè h = 0,7 ìì, âíóòðåííèé äèàìåòð d = 8 ìì, ïëîòíîñòü êðîâè

ρ = 1050 êã/ì

Ãëàâà 8. Áèîôèçèêà ñèñòåìû êðîâîîáðàùåíèÿ

253

ÂÎÏÐÎÑÛ ÒÅÑÒÎÂÎÃÎ ÊÎÍÒÐÎËß

8.1. Âÿçêîñòü êðîâè:

à) â ìåëêèõ ñîñóäàõ áîëüøå, ÷åì â êðóïíûõ;

á) â ìåëêèõ ñîñóäàõ ìåíüøå, ÷åì â êðóïíûõ;

â) ïîñòîÿííà âî âñåõ îòäåëàõ ñîñóäèñòîãî ðóñëà.

8.2. Ñ óâåëè÷åíèåì ãåìàòîêðèòà âÿçêîñòü êðîâè:

à) âîçðàñòàåò; â) íå èçìåíÿåòñÿ.

á) óáûâàåò;

8.3. Â êàêèõ ñîñóäàõ áîëüøå âåðîÿòíîñòü âîçíèêíîâåíèÿ òóðáóëåíò-

íîãî òå÷åíèÿ?

à) â êðóïíûõ; â) âîçíèêíîâåíèå òóðáóëåíòíîñòè

á) ìåëêèõ; íå çàâèñèò îò äèàìåòðà ñîñóäà.

8.4. Òå÷åíèå êðîâè ïî ñîñóäàì ÿâëÿåòñÿ:

à) âñåãäà ëàìèíàðíûì;

á) âñåãäà òóðáóëåíòíûì;

â) ïðåèìóùåñòâåííî ëàìèíàðíûì è ëèøü â íåêîòîðûõ ñëó÷àÿõ òóðáó-

ëåíòíûì;

ã) ïðåèìóùåñòâåííî òóðáóëåíòíûì è ëèøü â íåêîòîðûõ ñëó÷àÿõ ëà-

ìèíàðíûì.

8.5. Â êàêîì îòäåëå ñîñóäèñòîãî ðóñëà ëèíåéíàÿ ñêîðîñòü êðîâîòîêà

ìèíèìàëüíà?

à) â àîðòå; ã) êàïèëëÿðàõ;

á) àðòåðèÿõ; ä) âåíàõ.

â) àðòåðèîëàõ;

8.6. Îñíîâíîé äâèæóùåé ñèëîé êðîâîòîêà ÿâëÿåòñÿ:

à) ñòàòè÷åñêîå äàâëåíèå;

á) òðàíñìóðàëüíîå;

â) ãèäðîñòàòè÷åñêîå;

ã) êðîâÿíîå, îáóñëîâëåííîå ïðåâûøåíèåì äàâëåíèÿ, âûçâàííîãî ðà-

áîòîé ñåðäöà, íàä àòìîñôåðíûì äàâëåíèåì;

ä) ñèëà òÿæåñòè.

8.7. Êàêîé îòäåë ñîñóäèñòîãî ðóñëà îáëàäàåò íàèáîëüøèì ãèäðàâëè-

÷åñêèì ñîïðîòèâëåíèåì?

à) àîðòà; ã) êàïèëëÿðû;

á) àðòåðèè; ä) âåíû.

â) àðòåðèîëû;

8.8. Óâåëè÷åíèå òåíäåíöèè ýðèòðîöèòîâ ê àãðåãàöèè âûçûâàåò:

à) âîçðàñòàíèå ÑÎÝ; â) íå îòðàæàåòñÿ íà ÑÎÝ.

á) ñíèæåíèå ÑÎÝ;

8.9. Âðåìåííàÿ çàâèñèìîñòü äèàñòîëè÷åñêîãî äàâëåíèÿ, âû÷èñëåííàÿ

â ìîäåëè Ôðàíêà, èìååò âèä:

à)

()

;pptXC=+ ã)

;

á)

;ppCXt=+ ä)

ln .

â)

exp ;



=−





Ïðàêòè÷åñêèå è òåñòîâûå çàäàíèÿ

254

8.10. Ýëàñòè÷íîñòü êðîâåíîñíûõ ñîñóäîâ èìååò ñëåäóþùèé ýëåêòðè-

÷åñêèé ýêâèâàëåíò:

à) ýëåêòðè÷åñêèé ïîòåíöèàë; ã) ýëåêòðè÷åñêàÿ åìêîñòü;

á) ýëåêòðè÷åñêîå ñîïðîòèâëåíèå; ä) ýëåêòðè÷åñêèé òîê.

â) èíäóêòèâíîñòü;

8.11. Ñêîðîñòü ðàñïðîñòðàíåíèÿ ïóëüñîâîé âîëíû îïðåäåëÿåòñÿ ïî

ñëåäóþùåé ôîðìóëå:

à)

;

ã)

á)

;

ä) .

â)

;







8.12. Ïóëüñîâîé âîëíîé íàçûâàþòñÿ ïåðèîäè÷åñêèå êîëåáàíèÿ:

à) ñêîðîñòè ðàñïðîñòðàíåíèÿ ÷àñòèö;

á) ëèíåéíîé ñêîðîñòè êðîâîòîêà;

â) îáúåìíîé ñêîðîñòè êðîâîòîêà;

ã) ñòàòè÷åñêîãî äàâëåíèÿ;

ä) êðîâÿíîãî äàâëåíèÿ, òî åñòü ðàñïðîñòðàíÿþùèåñÿ âäîëü êðîâåíîñ-

íûõ ñîñóäîâ.

8.13. Ñêîðîñòè ðàñïðîñòðàíåíèÿ ÷àñòèö êðîâè (

v ), ïóëüñîâîé âîëíû

(

) è çâóêîâîé âîëíû (

) â êðîâè ñîîòíîñÿòñÿ ñëåäóþùèì îáðàçîì:

à)

пкз

;vvv<< ã)

пзк

;vvv<<

á)

кпз

;vvv<< ä)

зкп

.vvv<<

â)

зпк

;vvv<<

8.14. Ôèëüòðàöèè êðîâè ñïîñîáñòâóþò:

à) ãèäðîñòàòè÷åñêîå äàâëåíèå â êàïèëëÿðàõ è îíêîòè÷åñêîå äàâëåíèå

ïëàçìû;

á) ãèäðîñòàòè÷åñêîå äàâëåíèå â êàïèëëÿðàõ è îíêîòè÷åñêîå äàâëåíèå

òêàíåâîé æèäêîñòè;

â) ãèäðîñòàòè÷åñêîå äàâëåíèå â òêàíåâîé æèäêîñòè è îíêîòè÷åñêîå

äàâëåíèå ïëàçìû;

ã) ãèäðîñòàòè÷åñêîå äàâëåíèå â òêàíåâîé æèäêîñòè è îíêîòè÷åñêîå

äàâëåíèå òêàíåâîé æèäêîñòè.

8.15. Â íîðìàëüíûõ ôèçèîëîãè÷åñêèõ óñëîâèÿõ â êàïèëëÿðíîé ñåòè:

à) ôèëüòðàöèÿ íåìíîãî ïðåâîñõîäèò ðåàáñîðáöèþ;

á) ðåàáñîðáöèÿ íåìíîãî ïðåâîñõîäèò ôèëüòðàöèþ;

â) ðåàáñîðáöèÿ ïîëíîñòüþ êîìïåíñèðóåò ôèëüòðàöèþ.

Ãëàâà 8. Áèîôèçèêà ñèñòåìû êðîâîîáðàùåíèÿ

Ãëàâà 9

ÝËÅÊÒÐÎÌÀÃÍÅÒÈÇÌ

Íàèáîëåå ðàñïðîñòðàíåííûå ÿâëåíèÿ, ñ êîòîðûìè ïðèõîäèòñÿ

ñòàëêèâàòüñÿ ÷åëîâåêó, ñâÿçàíû ñ ýëåêòðîìàãíèòíûì âçàèìîäåé-

ñòâèåì. Òàêîå âçàèìîäåéñòâèå ðàññìàòðèâàåòñÿ â ðàçäåëå ôèçèêè,

íàçûâàåìîì ýëåêòðîäèíàìèêîé.

Öåëûé ðÿä ÿâëåíèé, íà ïåðâûé âçãëÿä íå èìåþùèõ îòíîøåíèÿ

ê ýëåêòðîìàãíåòèçìó, íàïðèìåð: óïðóãîñòü, ñèëû òðåíèÿ, ðàáîòà

ðàçëè÷íûõ îðãàíîâ ÷óâñòâ æèâîòíûõ è ÷åëîâåêà, îáúÿñíÿåòñÿ ýëåê-

òðîìàãíèòíûì âçàèìîäåéñòâèåì. Îñîáóþ ðîëü ýòî âçàèìîäåéñòâèå

èãðàåò â ðàçëè÷íûõ áèîôèçè÷åñêèõ è áèîõèìè÷åñêèõ ïðîöåññàõ,

êîòîðûå íåâîçìîæíî èçó÷èòü, íå èìåÿ ôóíäàìåíòàëüíûõ ïðåäñòàâ-

ëåíèé î çàêîíàõ ýëåêòðîäèíàìèêè. Ïîëó÷èòü îñíîâàòåëüíûå çíà-

íèÿ â îáëàñòè âçàèìîäåéñòâèÿ õèìè÷åñêèõ âåùåñòâ ñ æèâûìè îðãà-

íèçìàìè ìîæíî òîëüêî ïðè ãëóáîêîì èçó÷åíèè ýëåêòðîìàãíåòèçìà.

§ 9.1. ÝËÅÊÒÐÎÑÒÀÒÈÊÀ

Ýëåêòðîñòàòèêîé íàçûâàåòñÿ ðàçäåë ýëåêòðîäèíàìèêè, â êî-

òîðîì ðàññìàòðèâàþòñÿ ñâîéñòâà è âçàèìîäåéñòâèå íåïîäâèæíûõ

â èíåðöèàëüíîé ñèñòåìå îòñ÷åòà ýëåêòðè÷åñêè çàðÿæåííûõ òåë èëè

÷àñòèö.

Ýëåêòðè÷åñêèé çàðÿä ðàâåí öåëîìó ÷èñëó ýëåìåíòàðíûõ çàðÿ-

äîâ, íîñèòåëÿìè êîòîðûõ ÿâëÿþòñÿ îòðèöàòåëüíî çàðÿæåííûå ÷à-

ñòèöû — ýëåêòðîíû è ïîëîæèòåëüíî çàðÿæåííûå — ïðîòîíû. Ýëå-

ìåíòàðíûå çàðÿäû ïðîòîíîâ è ýëåêòðîíîâ ðàâíû ïî ìîäóëþ, òî

åñòü

= å = 1,602•10

–19

Êë. Çàðÿä â ÑÈ èçìåðÿåòñÿ â êóëî-

íàõ (Êë). 1 êóëîí = 1 àìïåð-ñåêóíäà [À•ñ].

Â öåëîì ôèçè÷åñêèå îáúåêòû (òåëà) ýëåêòðè÷åñêè íåéòðàëüíû,

÷òî ÿâëÿåòñÿ ñëåäñòâèåì ç à ê î í à ñ î õ ð à í å í è ÿ ç à ð ÿ ä à, êî-

òîðûé ìîæíî ñôîðìóëèðîâàòü ñëåäóþùèì îáðàçîì: â èçîëèðîâàí-

íîé ñèñòåìå ñóììàðíûé ýëåêòðè÷åñêèé çàðÿä ðàâåí íóëþ, òî åñòü

256

∑

q . (9.1.1)

Åñëè ýëåêòðè÷åñêàÿ íåéòðàëüíîñòü òåëà íàðóøåíà, òî îíî ÿâ-

ëÿåòñÿ íàýëåêòðèçîâàííûì. Òàêîå òåëî ñàìî ïî ñåáå óæå íå ìîæåò

áûòü èçîëèðîâàííûì íè ïðè êàêèõ óñëîâèÿõ. Äëÿ ýëåêòðèçàöèè

òåëà íåîáõîäèìî, ÷òîáû íà íåì áûë ñîçäàí èçáûòîê (íåäîñòàòîê)

ýëåêòðè÷åñêèõ çàðÿäîâ òîãî èëè äðóãîãî çíàêà. Ýëåêòðè÷åñêèå çà-

ðÿäû ðàçëè÷íîãî çíàêà ïðèòÿãèâàþòñÿ, à îäíîèìåííûå — îòòàë-

êèâàþòñÿ.

Ñèëà âçàèìîäåéñòâèÿ ìåæäó äâóìÿ òî÷å÷íûìè çàðÿäàìè, òî åñòü

çàðÿäàìè, ëèíåéíûå ðàçìåðû êîòîðûõ íàìíîãî ìåíüøå ðàññòîÿ-

íèÿ ìåæäó íèìè, îïðåäåëÿåòñÿ ç à ê î í î ì Ê ó ë î í à:

πε ε

1212

012

qqr

; (9.1.2)

èëè â ñêàëÿðíîé ôîðìå

πε ε

012

, (9.1.3)

ãäå q

è q

— âçàèìîäåéñòâóþùèå çàðÿäû;

r — ðàäèóñ-âåêòîð,

ïðîâåäåííûé îò çàðÿäà 1 ê çàðÿäó 2;

F —

ñèëà, äåéñòâóþùàÿ ñî

ñòîðîíû çàðÿäà q

íà çàðÿä q

;

— ýëåêòðè÷åñêàÿ ïîñòîÿííàÿ,

= 8,85•10

–12

Ô/ì; ε — îòíîñèòåëüíàÿ äèýëåêòðè÷åñêàÿ ïðîíèöàå-

ìîñòü ñðåäû, ïîêàçûâàþùàÿ, âî ñêîëüêî ðàç â äàííîé ñðåäå ñèëà

âçàèìîäåéñòâèÿ ìåæäó çàðÿäàìè óìåíüøàåòñÿ ïî ñðàâíåíèþ ñ ñè-

ëîé âçàèìîäåéñòâèÿ â âàêóóìå. Ïðîèçâåäåíèå

εε=ε

, (9.1.4)

íàçûâàåòñÿ àáñîëþòíîé äèýëåêòðè÷åñêîé ïðîíèöàåìîñòüþ ñðåäû.

Ñèëîâûå õàðàêòåðèñòèêè ýëåêòðè÷åñêîãî ïîëÿ. Â ïðîñòðàíñòâå,

îêðóæàþùåì ýëåêòðè÷åñêèå çàðÿäû, ñóùåñòâóåò ìàòåðèàëüíàÿ ñðåäà,

íàçûâàåìàÿ ýëåêòðè÷åñêèì ïîëåì, ïîñðåäñòâîì êîòîðîãî îñóùåñòâ-

ëÿåòñÿ âçàèìîäåéñòâèå çàðÿäîâ. Êîëè÷åñòâåííîé ñèëîâîé õàðàêòå-

ðèñòèêîé ýëåêòðè÷åñêîãî ïîëÿ ÿâëÿåòñÿ åãî íàïðÿæåííîñòü, êîòî-

ðàÿ îïðåäåëÿåòñÿ â êàæäîé òî÷êå ïðîñòðàíñòâà êàê ñèëà,

äåéñòâóþùàÿ íà åäèíè÷íûé ïîëîæèòåëüíûé òî÷å÷íûé çàðÿä:

(,,)

xyz

. (9.1.5)

Ëþáîé çàðÿä ñîçäàåò âîêðóã ñåáÿ ýëåêòðè÷åñêîå ïîëå, à ëþáîé

çàðÿä, ïîìåùåííûé â ýëåêòðè÷åñêîå ïîëå, èñïûòûâàåò äåéñòâèå

Ãëàâà 9. Ýëåêòðîìàãíåòèçì

257

ýëåêòðè÷åñêîãî ïîëÿ, è ñàì èçìåíÿåò åãî. Ïðåäïîëàãàåòñÿ, ÷òî òî-

÷å÷íûé çàðÿä q äîñòàòî÷íî ìàë, íå ó÷àñòâóåò â ñîçäàíèè ýëåêòðè-

÷åñêîãî ïîëÿ è íå èñêàæàåò åãî. Òàêîé çàðÿä íàçûâàþò ïðîáíûì.

Èç ôîðìóë (9.1.5) è (9.1.2) ñëåäóåò, ÷òî íàïðÿæåííîñòü ïîëÿ,

ñîçäàâàåìîãî òî÷å÷íûì çàðÿäîì q, ðàâíà

πε ε

, (9.1.6)

èëè â ñêàëÿðíîé ôîðìå

πε ε

. (9.1.7)

ãäå

— ðàäèóñ-âåêòîð, ïðèâåäåííûé èç çàðÿäà q â èññëåäóåìóþ

òî÷êó ïîëÿ

Íàïðÿæåííîñòü ïîëÿ â ÑÈ èçìåðÿåòñÿ â âîëüòàõ íà ìåòð (Â/ì).

Äëÿ ãðàôè÷åñêîãî èçîáðàæåíèÿ ýëåêòðîñòàòè÷åñêèõ ïîëåé èñïîëü-

çóåòñÿ ïîíÿòèå ñèëîâûõ ëèíèé ïîëÿ. Ñèëîâûìè ëèíèÿìè ýëåêòðè÷å-

ñêîãî ïîëÿ íàçûâàþòñÿ êðèâûå, êàñàòåëüíûå ê êîòîðûì â ëþáîé

òî÷êå ñîâïàäàþò ñ íàïðàâëåíèåì âåêòîðà íàïðÿæåííîñòè

â ýòîé

òî÷êå. Ãóñòîòà ëèíèé âûáèðàåòñÿ òàê, ÷òîáû êîëè÷åñòâî ëèíèé,

ïðîíèçûâàþùèõ åäèíè÷íóþ,

ïåðïåíäèêóëÿðíóþ èì ïëî-

ùàäêó, áûëî ÷èñëåííî ðàâíî

âåêòîðó

. Çà ïîëîæèòåëü-

íîå íàïðàâëåíèå ñèëîâîé ëè-

íèè ïðèíÿòî ñ÷èòàòü íàïðàâ-

ëåíèå âåêòîðà

. Òàêèì

îáðàçîì, ñèëîâûå ëèíèè âû-

õîäÿò èç ïîëîæèòåëüíûõ çà-

ðÿäîâ è âõîäÿò â îòðèöàòåëü-

íûå (ðèñ. 9.1.1). Ëèíèè ýëåêòðè÷åñêîãî ïîëÿ íèãäå, êðîìå çàðÿäîâ,

íå íà÷èíàþòñÿ è íå çàêàí÷èâàþòñÿ.

Ñîãëàñíî ïðèíöèïó ñóïåðïîçèöèè ýëåêòðè÷åñêèõ

ïîëåé, íàïðÿæåííîñòü ýëåêòðè÷åñêîãî ïîëÿ ñèñòåìû íåïîäâèæíûõ

òî÷å÷íûõ çàðÿäîâ q

, q

, …, q

ðàâíà âåêòîðíîé ñóììå íàïðÿæåííîñ-

òåé, ñîçäàâàåìûõ â äàííîé òî÷êå êàæäûì èç ýòèõ çàðÿäîâ â îòäåëü-

íîñòè, òî åñòü

∑

. (9.1.8)

Ïîòîê âåêòîðà íàïðÿæåííîñòè ýëåêòðè÷åñêîãî ïîëÿ ÷åðåç ìà-

ëóþ ïîâåðõíîñòü ïëîùàäüþ ∆S ðàâåí

()

ESΦ= ⋅∆

, (9.1.9)

Ðèñ. 9.1.1. Ëèíèè ýëåêòðè÷åñêîãî ïîëÿ ïî-

ëîæèòåëüíîãî è îòðèöàòåëüíîãî çàðÿäîâ

§ 9.1. Ýëåêòðîñòàòèêà

258

ãäå ∆



S — ïñåâäîâåêòîð, ìîäóëü êîòîðîãî ðàâåí ïëîùàäè ∆S, à íà-

ïðàâëåíèå ñîâïàäàåò ñ íàïðàâëåíèåì âíåøíåé íîðìàëè



. Ðàçìåð

ýëåìåíòà ïîâåðõíîñòè ∆S âûáèðàåòñÿ òàêèì îáðàçîì, ÷òîáû íà-

ïðÿæåííîñòü ïîëÿ áûëà ïðèìåðíî îäèíàêîâà â êàæäîé òî÷êå ∆S.

Ïîòîê âåêòîðà



÷åðåç ïîâåðõíîñòü S ðàâåí ñóììå ïîòîêîâ ÷å-

ðåç êàæäûé åå ýëåìåíò ∆S

, òî åñòü

()()

∆→

→∞

Φ= ∆ =

∑

∫



lim d

ES ES. (9.1.10)

Òåîðåìà Ãàóññà äëÿ ýëåêòðîñòàòè÷åñêèõ ïîëåé:

ïðîèçâåäåíèå àáñîëþòíîé äèýëåêòðè÷åñêîé ïðîíèöàåìîñòè ñðåäû è ïî-

òîêà âåêòîðà



÷åðåç çàìêíóòóþ ïîâåðõíîñòü S ðàâíî àëãåáðàè÷å-

ñêîé ñóììå çàðÿäîâ, íàõîäÿùèõñÿ âíóòðè ýòîé ïîâåðõíîñòè:

()

εε ⋅ =

∑

∫





ES q

, (9.1.11)

ãäå q

— ñâîáîäíûå çàðÿäû, íàõîäÿùèåñÿ âíóòðè çàìêíóòîé ïîâåðõ-

íîñòè.

Åñëè ââåñòè âåêòîð ýëåêòðè÷åñêîé èíäóêöèè



=ε ε



, (9.1.12)

òî òåîðåìà Ãàóññà (9.1.11) ïðèìåò âèä:

∑

∫





DS q. (9.1.13)

Òåîðåìà Ãàóññà ïîçâîëÿåò âû÷èñëèòü íàïðÿæåííîñòü ýëåêòðè÷åñ-

êîãî ïîëÿ çàðÿæåííûõ òåë ðàçëè÷íîé êîíôèãóðàöèè.

Â ñëó÷àå áåñêîíå÷íîé îäíîðîäíî çàðÿæåííîé ïëîñêîñòè ëèíèè

íàïðÿæåííîñòè ýëåêòðè÷åñêîãî ïîëÿ íàïðàâëåíû ïåðïåíäèêóëÿð-

íî ïëîñêîñòè (åñëè ïëîñêîñòü çàðÿæåíà ïîëîæèòåëüíî, òî ëèíèè

íà íåé íà÷èíàþòñÿ; åñëè îòðèöàòåëüíî, òî — çàêàí÷èâàþòñÿ) è

ðàñïðåäåëåíû â ïðîñòðàíñòâå ðàâíîìåðíî (ðèñ. 9.1.2). Ïîýòîìó ïîëå,

ñîçäàâàåìîå áåñêîíå÷íîé ïëîñêîñòüþ, îäíîðîäíî è ðàâíî

εε

, (9.1.14)

ãäå

— ïîâåðõíîñòíàÿ ïëîòíîñòü çàðÿäà, òî åñòü çàðÿä åäèíèöû

ïëîùàäè ïîâåðõíîñòè,

σ=

σ=[]

Êë/ì

Ýëåêòðè÷åñêóþ èíäóêöèþ ÷àñòî íàçûâàþò ýëåêòðè÷åñêèì ñìåùåíèåì.

Ãëàâà 9. Ýëåêòðîìàãíåòèçì

259

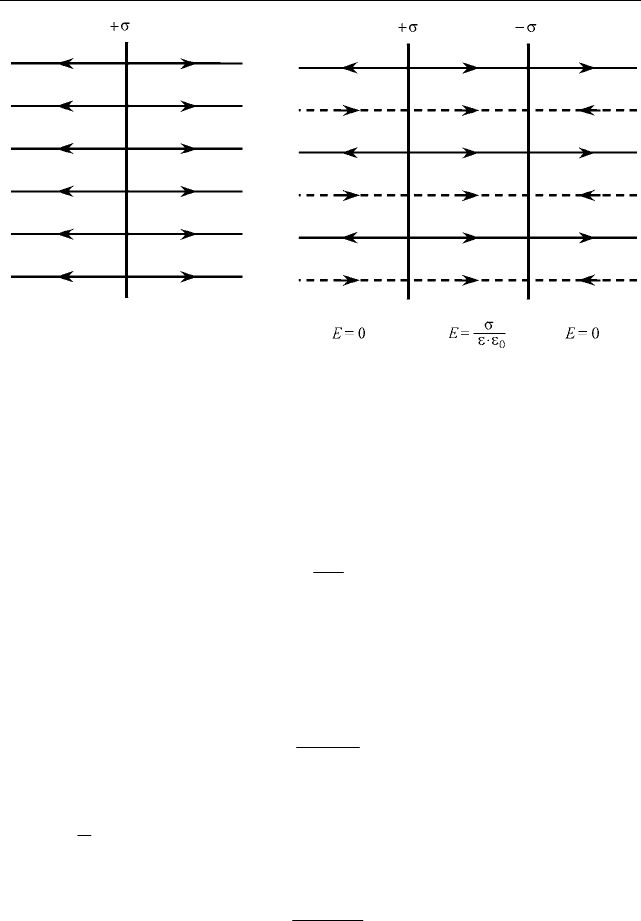
Â ñëó÷àå äâóõ áåñêîíå÷íûõ ðàçíîèìåííî çàðÿæåííûõ ïàðàëëåëü-

íûõ ïëîñêîñòåé (ïëîñêîãî êîíäåíñàòîðà) âñå ïîëå ñîñðåäîòî÷åíî

â ïðîìåæóòêå ìåæäó íèìè. Ýòî ïîëå îäíîðîäíî è ðàâíî

εε

, (9.1.15)

â òî âðåìÿ êàê ðåçóëüòèðóþùàÿ íàïðÿæåííîñòü ïîëÿ âíå ïëîñêî-

ñòåé ðàâíà íóëþ (ðèñ. 9.1.3).

Íàïðÿæåííîñòü ïîëÿ, ñîçäàííîãî áåñêîíå÷íîé ïðÿìîëèíåéíîé

ðàâíîìåðíî çàðÿæåííîé íèòüþ, ñîñòàâëÿåò íà ðàññòîÿíèè α îò íåå:

πε ε

, (9.1.16)

ãäå τ — ëèíåéíàÿ ïëîòíîñòü çàðÿäà íà íèòè — çàðÿä åäèíèöû äëè-

íû,

τ=

, τ=[] Êë/ì.

Íàïðÿæåííîñòü ïîëÿ, ñîçäàííîãî çàðÿæåííûì øàðîì ðàäèóñà

πε ε

, (9.1.17)

ãäå

— çàðÿä øàðà;

— ðàññòîÿíèå îò öåíòðà øàðà äî òî÷êè,

â êîòîðîé òðåáóåòñÿ íàéòè íàïðÿæåííîñòü, ïðè÷åì

Ðèñ. 9.1.2. Ïîëå áåñêîíå÷íîé

îäíîðîäíî çàðÿæåííîé (ïîëî-

æèòåëüíî) ïëîñêîñòè:

σ — ïîâåðõíîñòíàÿ ïëîòíîñòü çàðÿäà

Ðèñ. 9.1.3. Ïîëå äâóõ áåñêîíå÷íûõ ðàçíî-

èìåííî çàðÿæåííûõ ïëîñêîñòåé:

ñïëîøíûìè ëèíèÿìè ïîêàçàíî ïîëå ïîëîæèòåëüíî

çàðÿæåííîé ïëîñêîñòè; ïóíêòèðíûìè — îòðèöàòåëü-

íî çàðÿæåííîé

§ 9.1. Ýëåêòðîñòàòèêà

260

Ýíåðãåòè÷åñêèå õàðàêòåðèñòèêè ýëåêòðè÷åñêîãî ïîëÿ. Åñëè íà çà-

ðÿä q â ýëåêòðè÷åñêîì ïîëå äåéñòâóåò ñèëà =



FqE

, òî, ïåðåìåùàÿ

çàðÿä èç òî÷êè 1 â òî÷êó 2 íà ðàññòîÿíèå



, ýëåêòðè÷åñêîå ïîëå

ñîâåðøàåò ðàáîòó, ðàâíóþ

∫∫



ddAFlqEl, (9.1.18)

ãäå



d l

— íàïðàâëåíèå ýëåìåíòàðíîãî ïåðåìåùåíèÿ.

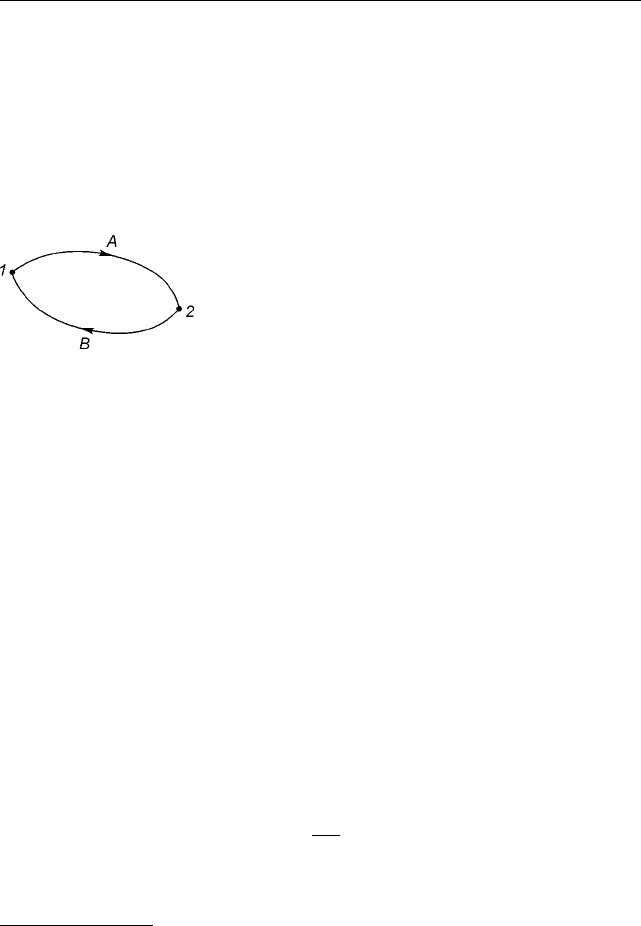
Ïóñòü çàðÿä ñîâåðøàåò ïåðåìåùåíèå ïî çàìê-

íóòîé òðàåêòîðèè 1-À-2-Â-1 (ðèñ. 9.1.4). Ïðè ýòîì

ïîòåíöèàëüíàÿ ýíåðãèÿ, çàâèñÿùàÿ òîëüêî îò

âçàèìíîãî ðàñïîëîæåíèÿ çàðÿäîâ è îò èõ ïîëî-

æåíèÿ âî âíåøíåì ñèëîâîì ïîëå, íå èçìåíÿåò-

ñÿ, à ñëåäîâàòåëüíî, ñèñòåìà íå ñîâåðøàåò ðàáî-

òó, òî åñòü ðàáîòà ñèë ýëåêòðîñòàòè÷åñêîãî ïîëÿ

ïî ïåðåìåùåíèþ çàðÿäà íà çàìêíóòîé òðàåêòî-

ðèè ðàâíà íóëþ:

==+=

∫∫∫





ddd0A q El qEl qEl , (9.1.19)

îòêóäà

qEdl qEdl=−

∫∫



. (9.1.20)

Èç ôîðìóëû (9.1.20) ñëåäóåò, ÷òî ðàáîòà ïî ïåðåìåùåíèþ çàðÿäà èç

ïîëîæåíèÿ 1 â ïîëîæåíèå 2 ðàâíà âçÿòîé ñ îáðàòíûì çíàêîì ðàáîòå ïî

ïåðåìåùåíèþ ýòîãî çàðÿäà â ïðîòèâîïîëîæíîì íàïðàâëåíèè.

Òàêèì îáðàçîì, ðàáîòà ïåðåìåùåíèÿ çàðÿäà íå çàâèñèò îò òðà-

åêòîðèè äâèæåíèÿ çàðÿäà, à îïðåäåëÿåòñÿ òîëüêî ïîëîæåíèåì íà-

÷àëüíîé è êîíå÷íîé òî÷åê. Ñëåäîâàòåëüíî, ýëåêòðîñòàòè÷åñêîå ïîëå

ÿâëÿåòñÿ ïîëåì êîíñåðâàòèâíûõ ñèë (ñì. § 2.2) è ìîæåò áûòü îõà-

ðàêòåðèçîâàíî ïîòåíöèàëîì.

Ïîòåíöèàë ïîëÿ â äàííîé òî÷êå ìîæíî îïðåäåëèòü ðàáîòîé

ïåðåìåùåíèÿ ïîëîæèòåëüíîãî çàðÿäà èç ýòîé òî÷êè íà áåñêîíå÷-

íîñòü

, äåëåííîé íà çíà÷åíèå ýòîãî çàðÿäà, òî åñòü

∞

ϕ=

. (9.1.21)

Èñõîäÿ èç ôîðìóëû (9.1.21), ðàáîòà ïî ïåðåìåùåíèþ çàðÿäà èç

òî÷êè 1 â òî÷êó 2 ðàâíà

Ïîòåíöèàë ïîëÿ ìîæåò áûòü îïðåäåëåí òîëüêî ñ òî÷íîñòüþ äî ïðîèçâîëü-

íîé ïîñòîÿííîé âåëè÷èíû. Íåîïðåäåëåííîñòü ïîòåíöèàëà óñòðàíÿþò, çàäàâ ïî-

ëîæåíèå, â êîòîðîì ïîòåíöèàë óñëîâíî ðàâåí íóëþ. Òàê, â òåîðåòè÷åñêèõ çàäà÷àõ

íóëþ ðàâåí ïîòåíöèàë áåñêîíå÷íî óäàëåííûõ òî÷åê, à íà ïðàêòèêå — ïîòåíöèàë

ïðîâîäíèêîâ, ñîåäèíåííûõ ñ Çåìëåé (çàçåìëåíèå).

Ðèñ. 9.1.4. Ê ïîÿñíåíèþ

ðàáîòû ýëåêòðè÷åñêîãî

ïîëÿ

Ãëàâà 9. Ýëåêòðîìàãíåòèçì