Волькенштейн М.В. Общая биофизика

Подождите немного. Документ загружается.

8.9.

ПЕРИОДИЧЕСКИЕ

ЯВЛЕНИЯ В МЕМБРАНАХ

451

§ 8.9. ПЕРИОДИЧЕСКИЕ

ЯВЛЕНИЯ

В МЕМБРАНАХ

Мембраны клеток и внутриклеточных органоидов в значи-

тельной степени определяют их свойства. Естественно

думать,

что и периодические процессы, присущие живым организмам,

связаны

с периодическими явлениями в мембранах.

Нелинейное

поведение

возбудимых

мембран отчетливо про-

является в генерации и распространении электрического им-

пульса

(см. гл. 5). Здесь мы рассмотрим периодические измене-

ния

состояния мембран, наблюдавшиеся в ряде опытов (см. [88]).

Теорелл показал, что в условиях взаи-

модействия ионного и объемного потоков

через мембрану возможно ее нестацио-

нарное

поведение вследствие периодиче-

ского изменения ионной проводимости

[89].

Теория этих явлений рассмотрена

далее. Шашуа наблюдал колебания элек-

трического потенциала в очень тонких

двойных полиэлектролитных мембранах

[90].

Двойной слой состоял из поликис-

лоты (а) и полиосноваиия (Р). Таким

образом, в нем имелись три зоны — от-

рицательно заряженная а, нейтральная

положительно заряженная р (рис.

8.36).

Мембрана помещалась

между

двумя

оди- Рис. 8.36. Схема

трех-

наковыми

растворами 0,15 М NaCl. При слойной_ полиэлектролит-

наложении

отрицательного потенциала

нои мем

аны

со стороны полиоснования (+) наблю-

дались периодические спайки и при некотором критическом зна-

чении

тока — незатухающие колебания, сохранявшиеся часами.

Ток

через мембрану состоит из перемещения катионов сквозь

зону а и анионов сквозь зону р. В

результате

в центральной

нейтральной зоне накапливается NaCl. Возрастание осмотиче-

ского давления приводит к появлению потока растворителя в

мембрану и возрастанию в ней гидростатического давления.

другой

стороны, увеличение концентрации соли вызывает

сокращение

молекул полиэлектролита, что также увеличи-

вает

гидростатическое давление. Когда это увеличение пре-

взойдет увеличение осмотического давления, поток растворителя

изменит

знак, и концентрация соли в мембране увеличится

еще больше. Возникает концентрационный градиент, соль

покидает мембрану и продолжает вытекать после того, как

мембрана достигнет максимального сокращения. Затем насту-

пает релаксация, возвращение мембраны в исходное состоя-

ние,

и процесс начинается сначала. Теоретическое рассмо-

трение этого автоколебательного процесса, поддерживаемого

f/ептр.

452

ГЛ. 8. НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

постоянной внешней силой, проведено Качальским и Спангле-

ром [88].

Мембранный осциллятор Теорелла [89] состоит из

двух

ячеек, заполненных электролитом разной концентрации и раз-

деленных мембраной из пористого стекла, содержащей связан-

ные отрицательные заряды. При пропускании постоянного тока

создается разность потенциалов на

двух

сторонах мембраны, и

в ячейках возникает сдвиг уровней жидкостей. При сильных по-

стоянных токах в системе происходят периодические колебания

уровней жидкостей и мембранного потенциала, разнящиеся по

фазе.

Это — электрокинетическое явление.

Вследствие

того, что

мембрана содержит фиксированные отрицательные заряды,

электролит в ее порах несет преимущественно катионы. Внеш-

ние

поля заставляют перемещаться катионы и растворитель.

Распределение концентраций в порах мембраны зависит от ко-

личества протекающей жидкости и

скорости ее течения, от

чего

зависит

сопротивление мембраны.

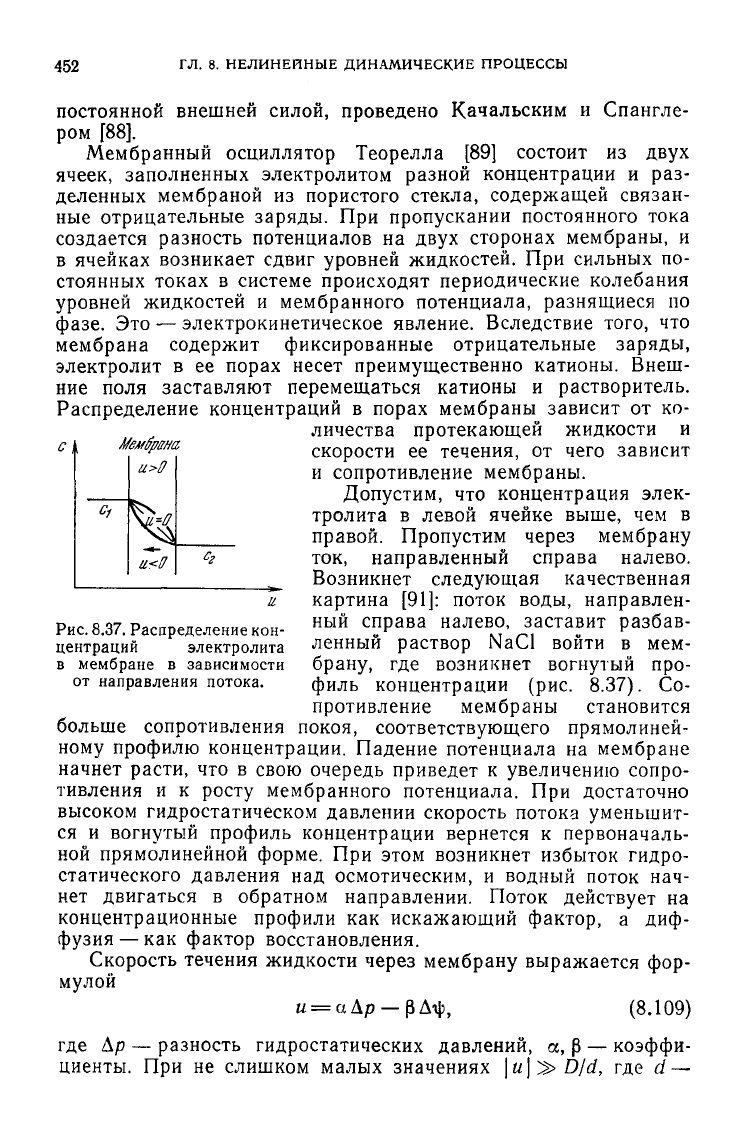
Допустим, что концентрация элек-

тролита в левой ячейке выше, чем в

правой. Пропустим через мембрану

ток, направленный справа налево.

Возникнет

качественная

и картина [91]: поток воды, направлен-

Рис.

8.37. Распределение

кон-

ный

?Р

ава

налево заставит разбав-

центраций электролита ленный раствор NaCl войти в мем-

в мембране в зависимости брану, где возникнет вогнутый про-

от направления потока.

иль

концентрации (рис.

8.37).

Со-

противление мембраны становится

больше сопротивления покоя,

соответствующего

прямолиней-

ному профилю концентрации. Падение потенциала на мембране

начнет расти, что в свою очередь приведет к увеличению сопро-

тивления и к

росту

мембранного потенциала. При достаточно

высоком гидростатическом давлении скорость потока уменьшит-

ся

и вогнутый профиль концентрации вернется к первоначаль-

ной

прямолинейной форме. При этом возникнет избыток гидро-

статического давления над осмотическим, и водный поток нач-

нет двигаться в обратном направлении. Поток

действует

на

концентрационные профили как искажающий фактор, а диф-

фузия— как фактор восстановления.

Скорость течения жидкости через мембрану выражается фор-

мулой

(8.109)

где Ар — разность гидростатических давлений, а, р —

коэффи-

циенты. При не слишком малых значениях \и\^> D/d, где d —

8.9.

ПЕРИОДИЧЕСКИЕ ЯВЛЕНИЯ

МЕМБРАНАХ

453

Pf Ps'P*

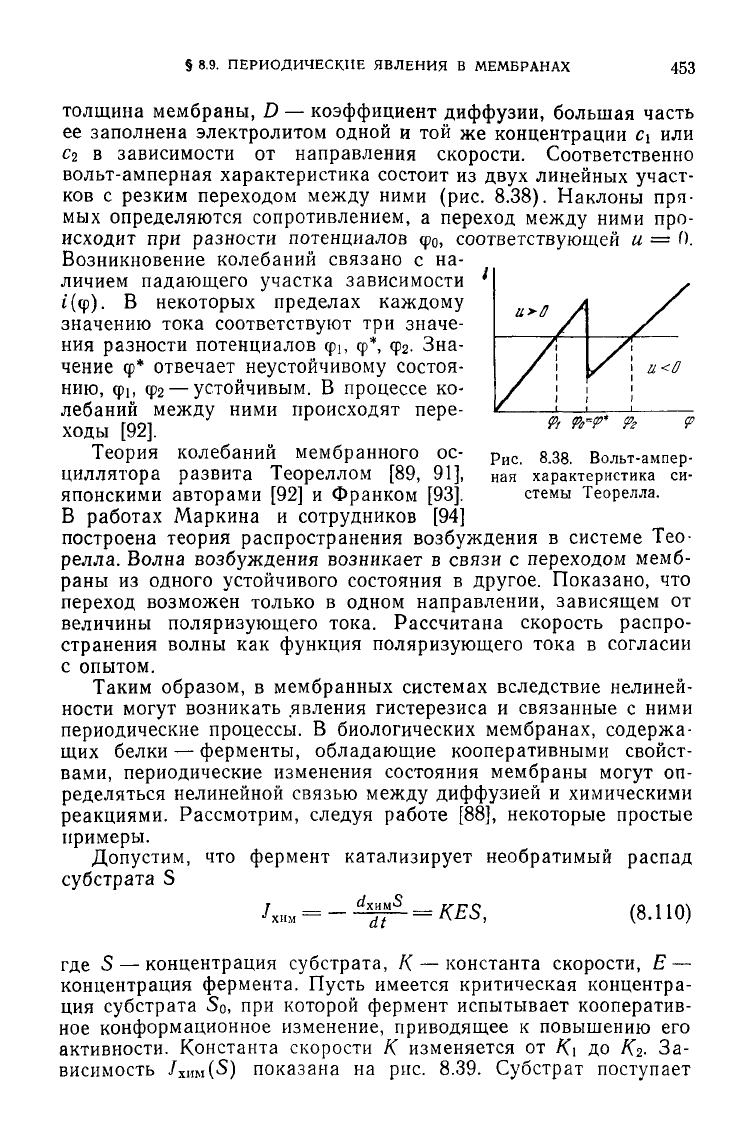
Рис.

8.38. Вольт-ампер-

ная

характеристика си-

стемы Теорелла.

толщина мембраны, D — коэффициент диффузии, большая часть

ее заполнена электролитом одной и той же концентрации С\ или

Сч в зависимости от направления скорости. Соответственно

вольт-амперная характеристика состоит из

двух

линейных

участ-

ков

с резким переходом

между

ними (рис.

8.38).

Наклоны пря-

мых определяются сопротивлением, а переход

между

ними про-

исходит при разности потенциалов ф

, соответствующей и = П.

Возникновение колебаний связано с на-

личием падающего участка зависимости

t(<p).

В некоторых пределах каждому

значению тока соответствуют три значе-

ния

разности потенциалов ф

ф*, Фг- Зна-

чение ф* отвечает неустойчивому состоя-

нию,

фь фг — устойчивым. В процессе ко-

лебаний

между

ними происходят пере-

ходы

[92].

Теория колебаний мембранного ос-

циллятора развита Теореллом [89, 91],

японскими

авторами [92] и Франком [93].

В работах Маркина и сотрудников [94]

построена теория распространения возбуждения в системе Тео-

релла. Волна возбуждения возникает в связи с переходом мемб-

раны из одного устойчивого состояния в

другое.

Показано, что

переход возможен только в одном направлении, зависящем от

величины поляризующего тока. Рассчитана скорость распро-

странения волны как функция поляризующего тока в согласии

с опытом.

Таким образом, в мембранных системах вследствие нелиней-

ности

могут

возникать явления гистерезиса и связанные с ними

периодические процессы. В биологических мембранах, содержа-

щих белки — ферменты, обладающие кооперативными свойст-

вами, периодические изменения состояния мембраны

могут

оп-

ределяться нелинейной связью

между

диффузией и химическими

реакциями.

Рассмотрим, следуя работе [88], некоторые простые

примеры.

Допустим, что фермент катализирует необратимый распад

субстрата S

" VIIM

•

= KES,

(8.110)

где S — концентрация субстрата, К — константа скорости, Е —

концентрация

фермента. Пусть имеется критическая концентра-

ция

субстрата S

, при которой фермент испытывает кооператив-

ное конформационное изменение, приводящее к повышению его

активности. Константа скорости К изменяется от К\ до /G- За-

висимость /

им(5) показана на рис. 8.39. Субстрат поступает

454

ГЛ. 8. НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

систему посредством диффузии через мембрану, идущей со

скоростью

/диф

— —21

— S),

(8.111)

где S

—концентрация S в источнике, которая считается прак-

тически ПОСТОЯННОЙ (S

= COnst). При /хим = /диф, S =

— 5хим +

ДИ

= 0 и система находится в стационарном со-

стоянии.

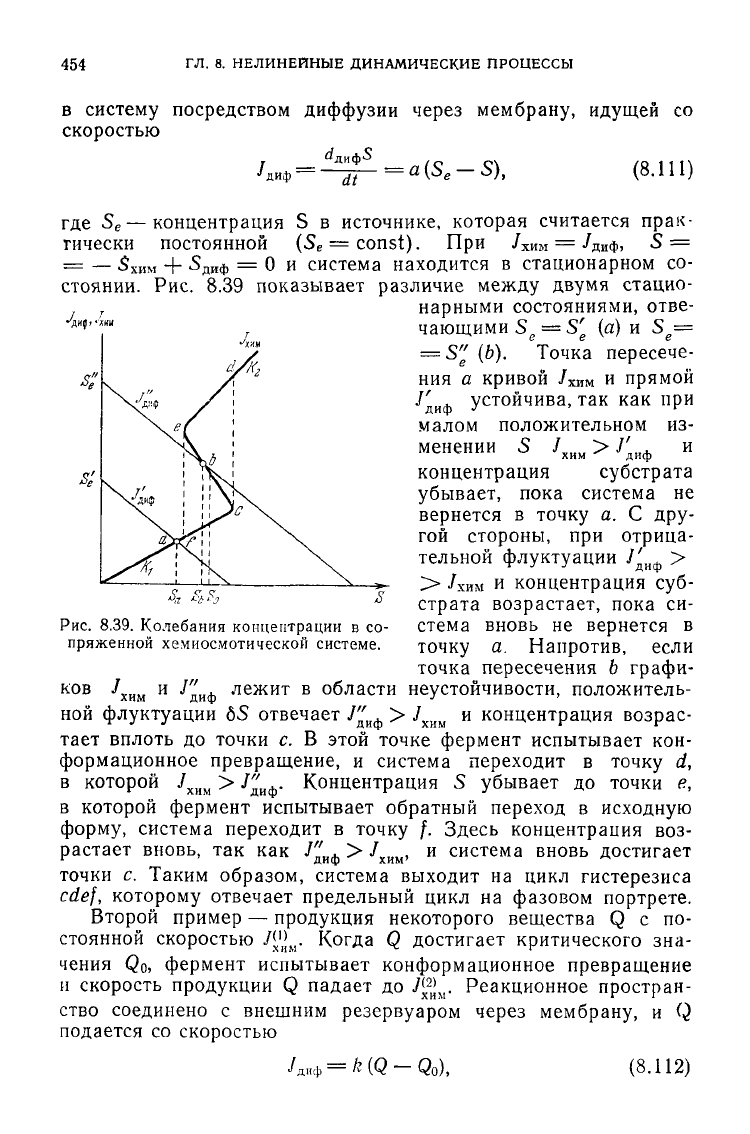
Рис. 8.39 показывает различие

между

двумя стацио-

нарными

состояниями, отве-

чающими S

= S'

(а) и S

S" (b). Точка пересече-

ния

а кривой /хим и прямой

Г устойчива,так как при

малом положительном из-

менении

хин

>/;

иф

концентрация

субстрата

убывает, пока система не

вернется в точку а. С дру-

гой стороны, при отрица-

тельной флуктуации /' >

> /хим и концентрация суб-

страта возрастает, пока си-

Рис.

8.39. Колебания концентрации в со- стема вновь не вернется в

пряженной

хемиосмотической системе. точку а. Напротив, если

точка пересечения b графи-

ков

^хим

^диф

лежит в

области неустойчивости, положитель-

ной

флуктуации 6S отвечает У" > /

хим

и концентрация возрас-

тает

вплоть до точки с. В этой точке фермент испытывает кон-

формационное

превращение, и система переходит в точку d,

которой /

хим

> /д

иф

. Концентрация S

убывает

до точки в,

которой фермент испытывает обратный переход в исходную

форму, система переходит в точку f. Здесь концентрация воз-

растает вновь, так как /д

Иф

> /

хим

, и система вновь достигает

точки с. Таким образом, система выходит на цикл гистерезиса

cdef,

которому отвечает предельный цикл на фазовом портрете.

Второй пример — продукция некоторого вещества Q с по-

стоянной

скоростью

Когда Q достигает критического зна-

чения

Qo, фермент испытывает конформационное превращение

скорость продукции Q падает до У^. Реакционное простран-

ство соединено с внешним резервуаром через мембрану, и Q

подается со скоростью

/ди

= k (Q - Q

(8.112)

8.10.

ФИБРИЛЛЯЦИЯ ВОЗБУДИМОЙ СРЕДЫ

455

так

что

диф-

(8.113)

Рис.

8.40.

Кооперативное

изменение проницаемости

мембраны

при Q = Qo.

В этом

случае

также возникают гистерезисная петля

коле-

бания.

Третий пример, рассмотренный Качальским

Спанглером

[88],

—

постоянный ферментативный процесс, сопряженный

с ко-

оперативным изменением проницаемости мембраны

от а\ до а

при

некотором значении концентрации продукта

Q (рис.

8.40).

Если мембрана разделяет

два

раствора

соли одинаковой концентрации

реак-

ция

мембране сама

продуцирует

ионы,

то концентрация соли внутри мембраны

отличается

от ее

концентрации

во

внеш-

ней

среде. Возникает разность потенциа-

лов, которая испытывает колебания, если

внутримембранный процесс кооперати-

вен.

Как

показывают

эти

примеры, коопе-

ративные свойства мембран

могут

быть

причиной

незатухающих

колебаний,

что

естественно,

так как

кооперативность

всегда

означает нелинейность.

Эти

явле-

ния

изучены, главным образом,

на экс-

периментальных

теоретических моде-

лях. Пока

отсутствуют

детальные исследования, раскрывающие

молекулярные механизмы мембранных процессов, ответствен-

ных

за

биологические ритмы. Однако общие

подходы

таким

проблемам развиты,

периодические процессы

клетках

нельзя более считать загадочными.

Обсуждаемые

явления можно феноменологически описать

на

языке нелинейной термодинамики

[88].

Задачи дальнейших

ис-

следований достаточно трудны,

так как их

решение

требует

де-

тального изучения молекулярной

структуры

динамики биоло-

гических мембран.

§ 8.10. ФИБРИЛЛЯЦИЯ ВОЗБУДИМОЙ

СРЕДЫ

Из

изложенного

в гл. 5

очевидно,

что

любая мышечная ткань

представляет собой

возбудимую

среду,

—

возбуждение, сообщае-

мое

сетью

нервных волокон, вызывает механохимические

про-

цессы.

Тем

самым процессы

возбудимых

средах

имеют

важ-

нейшее значение

для

физиологии,

частности,

для

физиологии

сердечной мышцы. Рассмотрим,

следуя

работам Кринского

([79,

95—99],

см.

также [19]),

фибрилляцию сердца. При

некоторых

патологических состояниях ритмически сокращающаяся сердеч-

456 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

ная

мышца десинхронизуется, отдельные мышечные волокна со-

кращаются хаотически, асинхронно, наступает фибрилляция,

приводящая

организм к гибели. Спасение может быть достиг-

нуто лишь быстрой дефибрилляцией, возвращением сердца к его

нормальному ритму. Физическая задача состоит в анализе при-

роды фибрилляции и условий ее возникновения, в нахождении

таких параметров системы, при воздействии на которые сердце

можно перевести в нормальный режим.

В § 8.5 рассмотрены возбудимые среды, в которых протекают

химические реакции. Визуально наблюдаемые в таких

средах

автоволновые процессы свойственны возбудимым средам в це-

лом.

В частности, циркуляция возбуждения в двумерной системе

приводит к общему для возбуждаемых сред явлению — к воз-

никновению

ревербераторов.

Само

понятие возбудимой среды как среды, в которой рас-

пространение импульса происходит без затухания, было введено

Винером и Розенблютом [42]. Импульс генерируется каждой

точкой среды. Примером одномерной возбудимой среды может

служить бикфордов шнур или нервное волокно. Каждая точка

возбудимой среды может находиться в одном из

трех

состояний:

покоя,

возбуждения и рефрактерности. Если на точку, находя-

щуюся в состоянии покоя, подать возбуждающий сигнал, то она

перейдет в возбужденное состояние, в котором пробудет время т,

затем перейдет в рефрактерное состояние, продолжающееся

течение времени т

. В период рефрактерности т

точка не реа-

гирует

более на возбуждающий сигнал, следовательно, никакая

точка не может возбуждаться с частотой, большей т~'.

Общие математические модели возбудимых сред, объясняю-

щие

возникновение ревербераторов, рассмотрены в работах [19,

42—45, 100]. Показано, что синхронное распространение волн

может нарушаться в

результате

появления источников волн, вы-

званного попаданием в

среду

внеочередного (экстрасистоличе-

ского) импульса возбуждения. В неоднородных

средах

эти

источники

могут

размножаться и порождать фибрилляцию.

Ревербератор в однородной двумерной системе возникает,

например,

при наличии отверстия, периметр которого превышает

длину волны К =

VXR

(V — скорость распространения волны).

Циркуляция

волны возбуждения возможна и в непрерывной

среде, неоднородной по рефрактерности. Если в некоторую об-

ласть среды, имеющую форму кольца, послать импульс, то он

не

будет

циркулировать, так как волны возбуждения, распро-

страняющиеся по часовой стрелке и против нее, встретятся и

погасят

друг

друга.

Однако если рефрактерность не

всюду

оди-

накова,

то циркуляция возникнет вследствие трансформации

ритма.

8.10.

ФИБРИЛЛЯЦИЯ ВОЗБУДИМОЙ СРЕДЫ

457

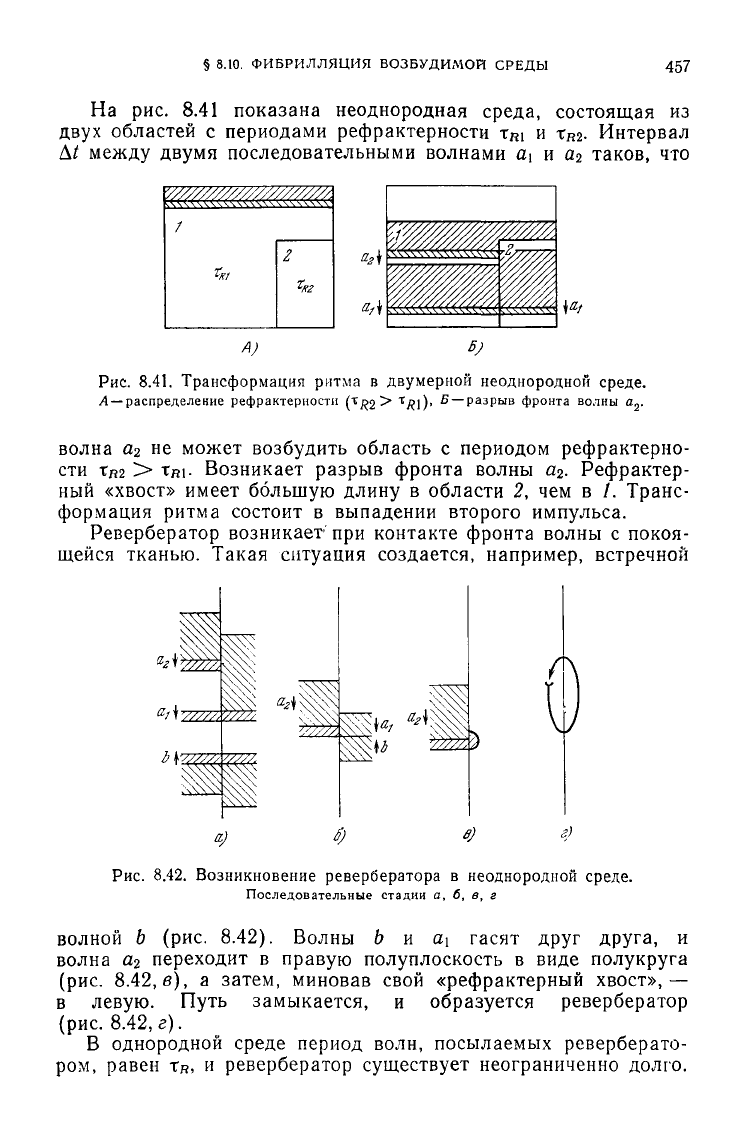
На

рис. 8.41

показана неоднородная среда, состоящая

из

двух

областей

периодами рефрактерности

2- Интервал

Д/

между

двумя последовательными волнами П\

И а

таков,

что

А)

Рис.

8.41. Трансформация ритма в двумерной неоднородной среде.

Л —распределение рефрактерности

(t^2>

R\)- ^

— разрыв фронта волны

волна

не

может возбудить область

периодом рефрактерно-

сти

Тд2 >

TRI.

Возникает разрыв фронта волны

Рефрактер-

ный

«хвост»

имеет большую длину

области

2, чем в /.

Транс-

формация

ритма состоит

выпадении второго импульса.

Ревербератор возникает

при

контакте фронта волны

покоя-

щейся

тканью. Такая ситуация создается, например, встречной

в)

Рис.

8.42. Возникновение ревербератора в неоднородной среде.

Последовательные стадии

а, б, в, г

волной

b (рис.

8.42).

Волны

b и а,\

гасят

друг

друга,

волна

переходит

правую полуплоскость

виде полукруга

(рис.

8.42, в), а

затем, миновав свой «рефрактерный

хвост»,—

левую. Путь замыкается,

образуется ревербератор

(рис.

8.42, г).

В однородной среде период волн, посылаемых реверберато-

ром,

равен

, и

ревербератор

существует

неограниченно долго.

458 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

Если

он возник на границе

двух

однородных областей, то его

время жизни конечно и тем меньше, чем больше неоднород-

ность.

Число оборотов волны возбуждения вокруг линии раз-

рыва фаз равно

П=1 +

Ф^-

8Л14

Размер ревербератора может быть меньше длины волны.

Ревербераторы

могут

сами служить источником волн высо-

кой

частоты, вызывающих появление новых ревербераторов.

Иными

словами, возможен процесс размножения реверберато-

ров.

В неоднородной среде ревербераторы посылают волны

с различными частотами и не синхронизуются. Если новые

источники

волн рождаются чаще, чем исчезают старые, то на-

блюдается сложная картина, напоминающая фибрилляцию.

Другой источник волн, не связанный с циркуляцией возбуж-

дения,

представляет собой так называемое эхо. Если подать не-

сколько

импульсов на неоднородное по периодам рефрактерно-

сти волокно, то на неоднородности появляются новые импульсы,

бегущие по волокну, и лишь позднее наступает состояние покоя.

Возникшие

импульсы подобны отраженным от неоднородности,

которая

рассматривается как источник эха. Кринский исследо-

вал условия возникновения эха, характеристики соответствую-

щего источника и их зависимости от параметров среды. Пока-

зано,

что эхо может появляться в

средах,

удовлетворяющих

условию т/тя > '/г- Начальные условия состоят в наличии доста-

точно большого разрыва в распределении фаз элементов по воз-

будимой среде. В неоднородной среде разрыв может возникать

при

трансформации ритма. Свойства источников эха близки

свойствам ревербератора, за исключением того, что размер

источников

эха может быть как угодно мал.

Ревербератор есть источник импульсов, который может су-

ществовать в среде и при т/т

< W Пути, по которым возбуж-

дение переходит из области с меньшей рефрактерностью в об-

ласть с большей рефрактерностью и обратно, пространственно

разделены, но сближаются при увеличении T/T

И при т/тд ^ '/г

соединяются. Тем самым эхо представляет собой предельный

случай ревербератора с нулевой длиной. Эхо и ревербератор

обладают одинаковыми свойствами как источники импульсов и

могут

быть причинами фибрилляции в неоднородных возбуди-

мых

средах.

В электрофизиологии состояние сердечной ткани характе-

ризуется так называемой «зоной уязвимости». Уязвимость озна-

чает возникновение более чем

двух

ответов при подаче на по-

лоску миокарда

двух

импульсов. Шириной зоны называется ди-

апазон

интервалов

между

импульсами At, при которых возни-

8.10. ФИБРИЛЛЯЦИЯ ВОЗБУДИМОЙ СРЕДЫ 459

кает уязвимость. Кринский показал, что уязвимость опреде-

ляется величиной х' = т/тд, ширина зоны тем меньше, чем

меньше т'.

В неоднородной возбудимой среде возникший источник волн,

будь

то эхо или ревербератор, может служить стимулятором для

запуска новых источников волн. Если параметры среды таковы,

что скорость «размножения» источников не меньше, чем ско-

рость их «умирания», то возможна фибрилляция. При взаимо-

действии нескольких источников длительность фибрилляции

быстро растет с увеличением т'. Минимальное число источников,

способное вызвать фибрилляцию заданной длительности, умень-

шается с увеличением т'. Опыт показывает, что на полоске ткани

миокарда фибрилляция может быть длительной, если размеры

самой полоски достаточно велики, т. е. имеется некоторая «кри-

тическая

масса»

для фибрилляции. Очевидно, что число источ-

ников,

обеспечивающее фибрилляцию, является аналогом кри-

тической массы.

Основной

вывод, полученный Кринским, состоит в том, что

безразмерный параметр т' является важной характеристикой

возбудимой среды, определяющей режим фибрилляции и время

его существования.

Применительно

к сердечной мышце в целом необходимо

найти

аналог величины т, выражающей длительность возбуж-

денного состояния, который можно измерить электрофизиологи-

ческими

методами. В качестве такой величины вводится время

возникновения

ответа на подаваемый импульс, т. е. латентный

период 0. Известно, что чем меньше амплитуда импульса, по-

даваемого на одиночную клетку, тем позже появляется ответ.

При

возбуждении двумя фиксированными стимулами 0 зависит

от времени Т, прошедшего после последнего возбуждения клетки

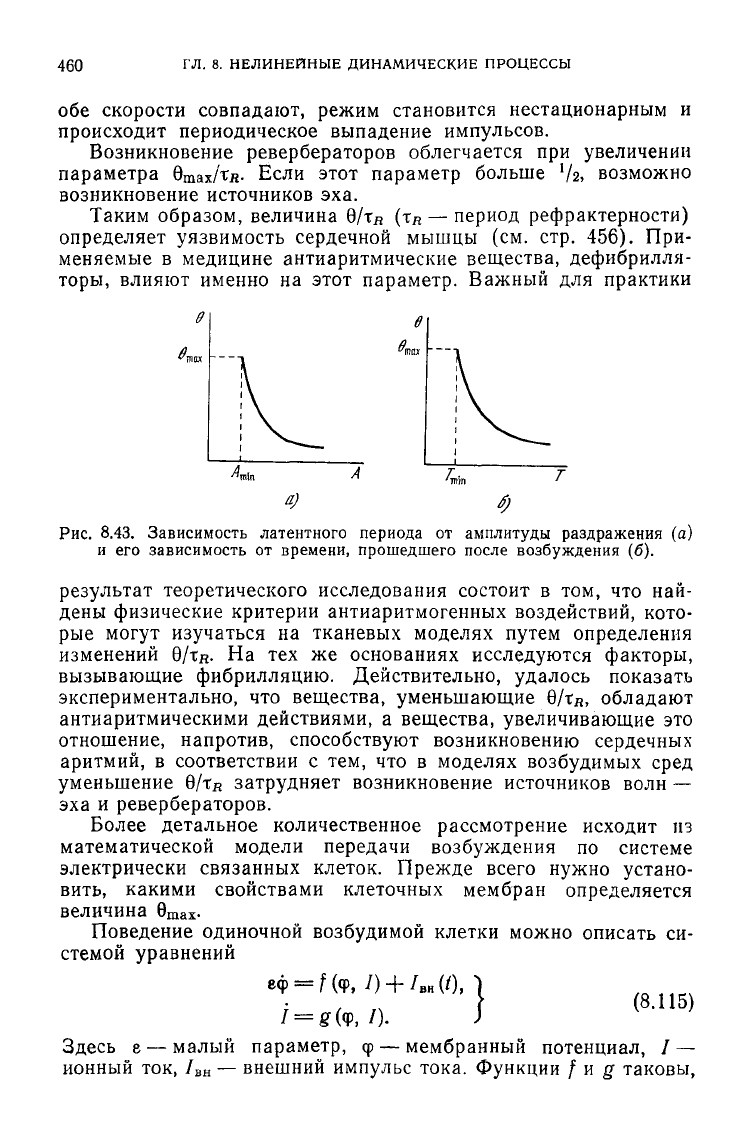
моменту прихода стимула (фаза клетки). Зависимость 0 от

амплитуды раздражения показана на рис. 8.43, а, зависимость

от фазы клетки Т — на рис.

8.43,6.

Существует максимальная

задержка

ах,

т. е. ответ не появляется при подпороговых сти-

мулах

А <.

min

и при Т

<7'

mln

Если клетка возбуждается не

стимулятором, а соседней клеткой, то при известном расстоянии

между

клетками график на рис. 8.43, б позволяет определить

скорость распространения возбуждения. Функция 0(Г) описы-

вает распространение возбуждения в системе. Теоретический

анализ

показывает, что каждому значению 0 отвечают два зна-

чения

скорости распространения возбуждения. Большая скорость

характеризует устойчивый процесс «горения», меньшая — не-

устойчивое

«тление»,

не наблюдаемое при периодическом следо-

вании

импульсов в стационарном режиме. При увеличении ча-

стоты следования импульсов меньшая скорость возрастает,

а большая уменьшается. При дальнейшем повышении частоты

460

ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ

ПРОЦЕССЫ

обе скорости совпадают, режим становится нестационарным и

происходит периодическое выпадение импульсов.

Возникновение

ревербераторов облегчается при увеличении

параметра

ах/Тя-

Если

ЭТОТ

параметр больше '/г, возможно

возникновение

источников эха.

Таким

образом, величина 0/т

(т

— период рефрактерности)

определяет уязвимость сердечной мышцы (см. стр. 456). При-

меняемые в медицине антиаритмические вещества, дефибрилля-

торы, влияют именно на этот параметр. Важный для практики

Рис.

8.43. Зависимость латентного периода от амплитуды раздражения (а)

его зависимость от времени, прошедшего после возбуждения (б).

результат

теоретического исследования состоит в том, что най-

дены физические критерии антиаритмогенных воздействий, кото-

рые

могут

изучаться на тканевых моделях путем определения

изменений

6/тн- На тех же основаниях исследуются факторы,

вызывающие фибрилляцию. Действительно, удалось показать

экспериментально,

что вещества, уменьшающие 0/т

, обладают

антиаритмическими действиями, а вещества, увеличивающие это

отношение,

напротив, способствуют возникновению сердечных

аритмий,

в соответствии с тем, что в моделях возбудимых сред

уменьшение 9/тд затрудняет возникновение источников волн —

эха и ревербераторов.

Более детальное количественное рассмотрение исходит нз

математической модели передачи возбуждения по системе

электрически

связанных клеток. Прежде всего нужно устано-

вить, какими свойствами клеточных мембран определяется

величина

та

х.

Поведение одиночной возбудимой клетки можно описать си-

стемой уравнений

/.(0.

Здесь е — малый параметр, ф — мембранный потенциал, / —

ионный

ток, /

вн

— внешний импульс тока. Функции / и g таковы,