Yu W., LaBoube R.A. Cold-Formed Steel Design

Подождите немного. Документ загружается.

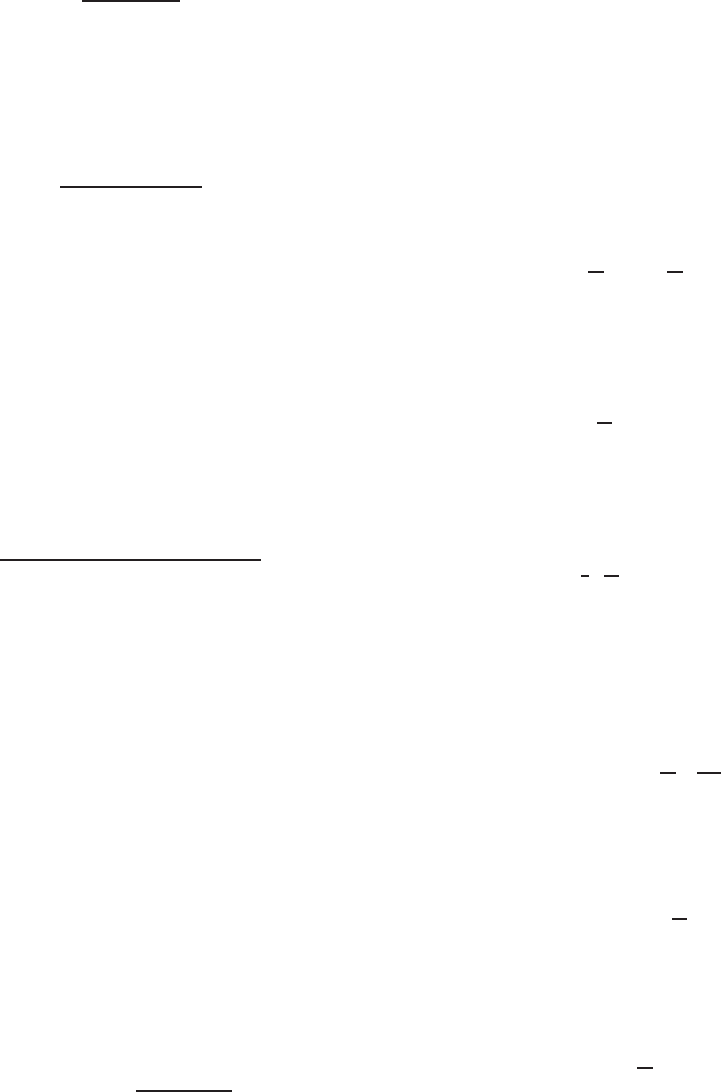
BENDING STRENGTH AND DEFLECTION 125

rigidity, which can be neglected without much loss in

economy. Therefore Eq. (4.38a) can be simpliﬁed as shown

in Eq. (4.39) by considering I

= I

+ I

and neglecting

the term of 4GJ(K

)

/π

EdI

)

(4.39)

Equation (4.39) was derived on the basis of a uniform

bending moment. It is rather conservative for the case of

unequal end moments. For this reason it may be modiﬁed

by multiplying the right-hand side by a bending coefﬁcient

1.161,3.84

as given in Eq. (4.40):

)

/dI

(4.40)

where C

is the bending coefﬁcient, which can conserva-

tively be taken as unity. During the period from 1968 to

1996, the bending coefﬁcient was calculated from C

1.75 + 1.05(M

) + 0.3(M

)

but must not exceed

2.3. Here M

is the smaller and M

the larger bending

moment at the ends of the unbraced length, taken about

the strong axis of the member. The ratio of end moments

is positive when M

and M

have the same sign

(reverse curvature bending) and negative when they are of

opposite signs (single curvature bending).

The above equation for C

was replaced by the following

equation in the 1996 edition of the AISI speciﬁcation and

is retained in the North American Speciﬁcation:

12.5M

max

2.5M

max

+ 3M

+ 4M

+ 3M

where M

max

= absolute value of maximum moment in

unbraced segment

= absolute value of moment at quarter point

of unbraced segment

= absolute value of moment at centerline of

unbraced segment

= absolute value of moment at three-quarter

point of unbraced segment

The above equation for bending coefﬁcient C

was

derived from Ref. 4.156. It can be used for various shapes

of moment diagrams within the unbraced segment and gives

more accurate results for ﬁxed-end beams and moment

diagrams which are not straight lines.

Consequently, the simpliﬁed, elastic critical moment for

lateral–torsional buckling of doubly symmetric I-beams

can be calculated from the elastic critical buckling stress

given in Eq. (4.40) and the section modulus relative to the

compression ﬁber as follows:

(

)

= σ

EdI

)

(4.41)

The above design formula was used in Section C3.1.2 (b)

of the 1996 edition of the AISI Speciﬁcation for doubly

symmetric I-sections except that K

= 1andL

= L.In

the North American Speciﬁcation, Section C3.1.2.1(b) is

based on Eq. (4.41) for the design of doubly symmetric

I-sections and singly symmetric C-sections.

It should be noted that Eq. (4.40) applies to elastic

buckling of cold-formed steel beams when the computed

theoretical buckling stress is less than or equal to the

proportional limit σ

. However, when the computed stress

exceeds the proportional limit, the beam behavior will be

governed by inelastic buckling. For extremely short beams,

the maximum moment capacity may reach the full plastic

moment M

for compact sections. A previous study

4.16

has

indicated that for wide-ﬂange beams having an average

shape factor of 10/9,

(4.42)

where M

= full plastic moment

= yield moment, = S

This means that the stress in extreme ﬁbers may reach

a hypothetical value of

when L

/dI

∼

0ifthe

elastic section modulus is used to compute the moment.

As in the previous design approach for compression

members (Ref. 1.4), the effective proportional limit (or the

upper limit of the elastic buckling) may be assumed to be

equal to one-half the maximum stress, that is,





= 0.56F

(4.43)

As shown in Fig. 4.26, assuming K

= 1andL

L, the corresponding L

/dI

ratio for σ

= σ

1.8π

When the theoretical critical stress exceeds σ

, the crit-

ical stress for inelastic buckling may be represented by the

following parabolic equation:

(σ

)

= F



A −





(4.44)

where A and B are constants that can be determined by the

following conditions:

1. When L = 0,

(σ

)

(4.45)

2. When L

/(dI

) = 1.8π

(σ

)

= 0.56F

(4.46)

By solving Eq. (4.44), A and B are found as follows:

A =

(4.47)

B = 3.24 (4.48)

126 4 FLEXURAL MEMBERS

Figure 4.26 Maximum lateral–torsional buckling stress for I-

beams (K

= 1andL

=L).

Therefore Eq. (4.44) can be rewritten as

(

)

= F



−

3.24



(

)





1 −



(

)



(4.49)

where

(

)

is the elastic buckling stress for

lateral–torsional buckling a nd

(

)

is the theoretical

equation for lateral–torsional buckling in the inelastic

range.

Even though the maximum stress computed by Eq. (4.49)

as shown in Fig. 4.26 is larger than F

, a conservative

approach has been used by AISI to limit the maximum

stress to F

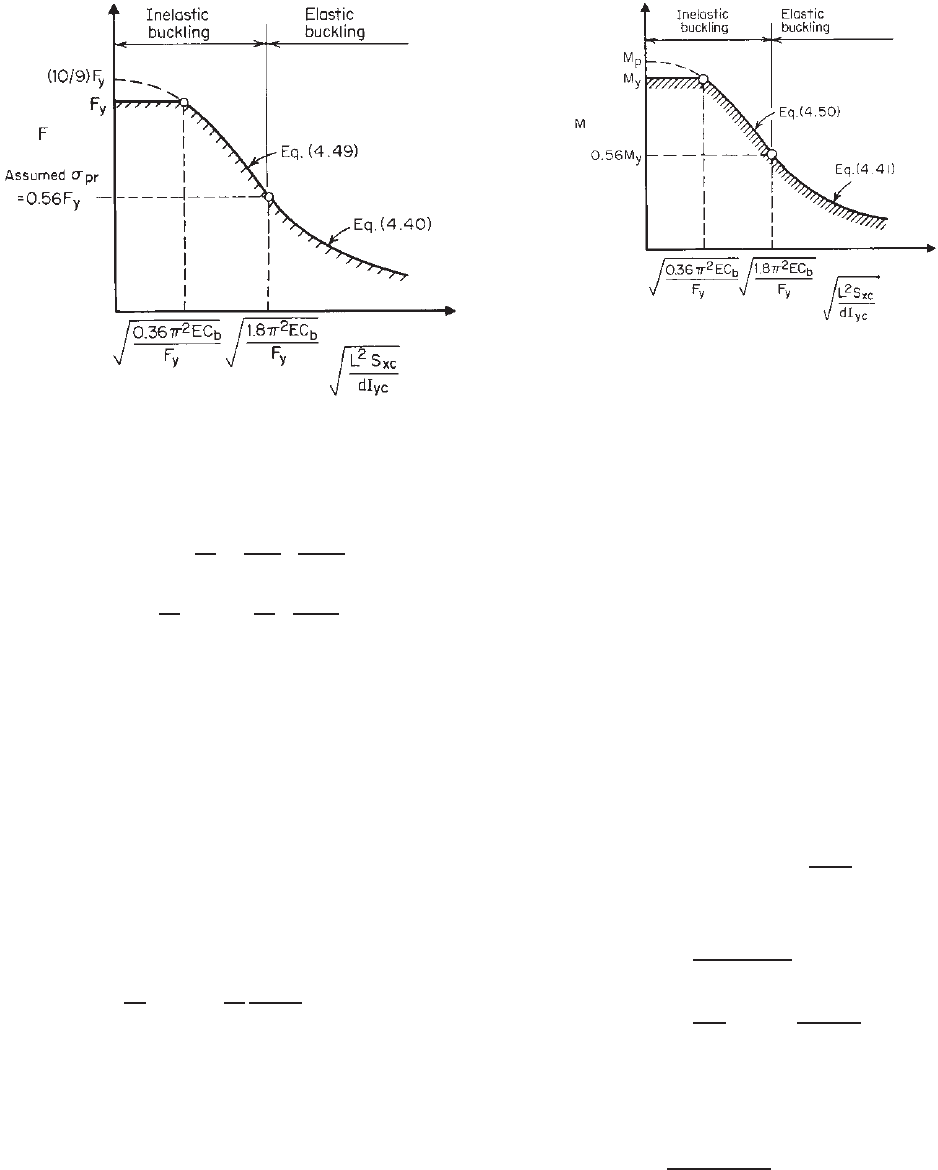
By using the inelastic critical buckling stress given in Eq.

(4.49) and the section modulus relative to the compression

ﬁber, the inelastic critical moment for lateral–torsional

buckling of I-beams can be computed as follows:

)

= (σ

)

≤ M



1 −

)



≤ M

(4.50)

where M

is the yield moment and (M

)

is the elastic

critical moment deﬁned in Eq. (4.41). Equation (4.50) was

used in Section C3.1.2 of the 1996 edition of the AISI

Speciﬁcation. It was used only for (M

)

> 0.56M

shown in Fig. 4.27. Hill has demonstrated that the equations

derived for I-sections can also be used for channels with

satisfactory accuracy.

4.17

For cold-formed steel design, Eqs. (4.40) and (4.49) were

used in the 1968 and 1980 editions of the AISI Speciﬁcation

Figure 4.27 Maximum lateral–torsional buckling moment for

I-beams (K

= 1andL

= L).

to develop the design equations for lateral–torsional buck-

ling of I-beams and channels. In the 1986 and 1996 editions

of the AISI Speciﬁcation, in addition to the use of Eqs.

(4.41) and (4.50) for determining the critical moment, new

design formulas for lateral–torsional buckling strength were

added as alternative methods. These additional equations

were developed from the previous study conducted by

Pekoz and Winter on ﬂexural–torsional buckling of thin-

walled sections under eccentric load. The AISI Speciﬁ-

cation also considers the effect of local buckling on the

lateral–torsional buckling strength of beams.

Speciﬁcally, Section C3.1.2 of the 1996 edition of the

AISI Speciﬁcation provided Eq. (4.51) for computing the

elastic critical moment on the basis of the ﬂexural–torsional

buckling theory. It is used for singly and doubly symmetric

sections bending about the symmetry axis perpendicular to

the web:

)

= C

√

(4.51)

where A is the full cross-sectional area and

)

(4.52)



GJ +

)



(4.53)

where K

= effective length factors for bending about

the y axis and for twisting

= unbraced length for bending about the y

axis and for twisting



+ r

+ x

= radii of gyration of the cross section

about the centroidal principal axes

BENDING STRENGTH AND DEFLECTION 127

= distance from the shear center to the

centroid along the principal x axis, taken

as negative

Other terms were deﬁned previously. For singly symmetric

sections, the x axis is the axis of symmetry oriented such

that the shear center has a negative x coordinate. The

basis for Eq. (4.51) is discussed by Pekoz in Ref. 3.17.

A comparison of Eqs. (4.41) and (4.51) shows that these

two equations give similar results for channels having

3.17

However, for channel sections having I

with large K

ratios, the simpliﬁed Eq. (4.41)

provides very conservative results as compared with Eq.

(4.51).

For singly symmetric sections bending about the

centroidal axis perpendicular to the symmetry axis, the

elastic critical moment based on the ﬂexural–torsional

buckling theory can be computed by using Eq. (4.54):

)

Aσ

[j + C



+ r

(σ

/σ

)]

(4.54)

where C

=+1 for moment causing compression on

shear center side of centroid

= –1 for moment causing tension on shear

center side of centroid

= π

E/(K

)

(4.55)

= 0.6 − 0.4(M

),whereM

is the smaller

and M

the larger bending moment at the

ends of the unbraced length and M

,the

ratio of end moments, is positive when M

and M

have the same sign (reverse

curvature bending) and negative when they

are of opposite sign (single curvature

bending). When the bending moment at any

point within an unbraced length is larger

than that at both ends of this length and for

members subject to combined axial load and

bending moment, C

shall be taken as

unity.

= effective length factor for bending about the

x axis

= unbraced length for bending about the x axis

and

j =





dA +





− x

(4.56)

= β

/2 (see Appendix C for computation of β

)

(4.57)

Other terms were deﬁned previously.

Figure 4.28 Elastic and inelastic critical lateral buckling

moments for members bending about centroidal axis perpendicular

to the web.

The derivation of Eq. (4.54) is presented in Chapter 6

for beam–columns. See Eqs. (6.46) and (6.50).

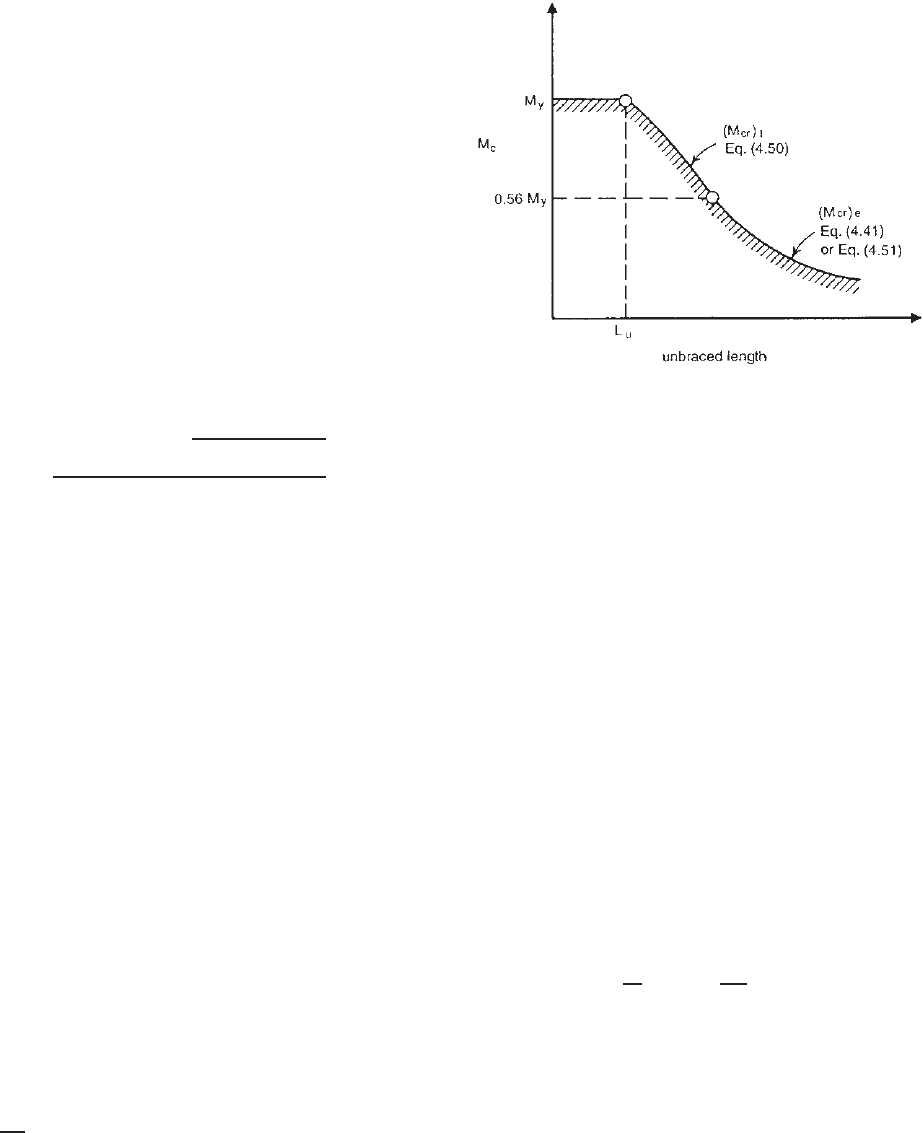
It should be noted that Eqs. (4.51) and (4.54) can be used

only when the computed value of (M

)

does not exceed

0.56M

, which is considered to be the upper limit for the

elastic buckling range. When the computed (M

)

exceeds

0.56M

, the inelastic critical moment can be computed from

Eq. (4.50). The elastic and inelastic critical moments are

shown in Fig. 4.28.

The above discussion dealt only with the lateral–torsional

buckling strength of locally stable beams. For locally

unstable beams, the interaction of the local buckling of

compression elements and the overall lateral–torsional

buckling of beams may result in a reduction of the

lateral–torsional buckling strength of the member. The

effect of local buckling on the critical moment was consid-

ered in Section C3.1.2 of the 1986 and 1996 editions of the

AISI speciﬁcation, in which the nominal lateral–torsional

buckling strength w as determined as follows:

= M





= S





= S

(4.58)

where M

= elastic or inelastic critical moment whichever

is applicable

= elastic section modulus of effective section

calculated a t stress F

(= M

) in extreme

compression ﬁber

= elastic section modulus of full unreduced

section for extreme compression ﬁber

= elastic or inelastic critical lateral–torsional

buckling stress

128 4 FLEXURAL MEMBERS

Table 4.2 Coefﬁcients K in Eq. (4.59)

3.3

Loads Act At

Centroid Top Flange Bottom Flange

0.4 86.4 51.3 145.6

4 31.9 20.2 50.0

8 25.6 17.0 38.2

16 21.8 15.4 30.4

24 20.3 15.0 27.2

32 19.6 14.8 26.3

48 19.0 14.8 23.5

64 18.3 14.9 22.4

80 18.1 14.9 21.7

96 17.9 15.1 21.1

160 17.5 15.3 20.0

240 17.4 15.6 19.3

320 17.2 15.7 18.9

400 17.2 15.8 18.7

In Eq. (4.58), the ratio of S

was used to account for the

effect of local buckling on the lateral–torsional buckling

strength of beams. The same design concept is used in the

North American Speciﬁcation.

The equations developed above for the uniform bending

moment can also be used for other loading conditions with

reasonable accuracy.

1.161,4.18

If more accurate results are

desired, the theoretical critical value for a concentrated load

at the center of a simply supported beam can be computed

3.3

= K



(4.59)

where K is a coefﬁcient to be taken from Table 4.2 based

on the parameter GJL

/EC

. For symmetrical I-sections,

 I

/4, where d is the depth of the section.

For a uniformly distributed load, the critical load is

= K



(4.60)

where K is to be taken from Table 4.3.

4.2.3.2 Point-Symmetric Sections Point-symmetric sec-

tions such as Z-sections with equal ﬂanges will buckle later-

ally at lower strengths than doubly and singly symmetric

sections. A conservative design approach has been used in

the AISI Speciﬁcation and is being used in the North Amer-

ican Speciﬁcation, in which the elastic critical moment is

taken to be one-half of those permitted for I-beams or chan-

nels. Therefore instead of using Eq. (4.51), the following

equation is used for determining the elastic critical moment

for point-symmetric Z-sections bending about the centroidal

Table 4.3 Coefﬁcients K in Eq. (4.60)

3.3

Loads Act At

Centroid Top Flange Bottom Flange

0.4 143.0 92.9 222.0

4 53.0 36.3 77.3

8 42.6 30.4 59.4

16 36.3 27.4 48.0

24 33.8 26.6 43.4

32 32.6 26.1 40.4

48 31.5 25.8 37.6

64 30.5 25.7 36.2

80 30.1 25.7 35.1

128 29.0 26.0 33.3

200 29.0 26.4 32.1

280 28.8 26.5 31.4

360 28.7 26.6 31.0

400 28.6 26.6 30.7

axis perpendicular to the web:

)

√

) (4.61)

In lieu of Eq. (4.61), the following simpliﬁed equation

can be used to calculate the elastic critical moment for Z-

sections:

(

)

EdI





(4.62)

All symbols used in Eqs. (4.61) and (4.62) are deﬁned in

Section 4.2.3.1.

4.2.3.3 North American Design Criteria for Lateral–

Torsional Buckling Strength of Singly, Doubly, and Point-

Symmetric Sections The following excerpts are adapted

from Section C3.1.2.1 of the 2007 edition of the North

American Speciﬁcation, which provides the needed design

equations for computing the critical lateral–torsional buck-

ling stress.

1.345

The application of the North American

design criteria is illustrated in Examples 4.9–4.11.

C3.1.2.1 Lateral–Torsional Buckling Strength

[Resistance] of Open Cross-Section Members

The provisions of Section C3.1.2.1 of the speciﬁcation shall

apply to I-, Z-, C-, and other singly symmetric section ﬂexural

members (not including multiple-web deck, U- and closed

box-type members, and curved or arch members) subject

to lateral–torsional buckling. The provisions of this section

shall not apply to laterally unbraced compression ﬂanges of

otherwise laterally stable sections. See Section 4.2.5 for C- and

Z-purlins in which the tension ﬂange is attached to sheathing.

BENDING STRENGTH AND DEFLECTION 129

For laterally unbraced segments of singly, doubly,and

point-symmetric sections subject to lateral–torsional buckling,

the nominal ﬂexural strength [moment resistance], M

,shall

be calculated in accordance with the equation

= S

(4.63)



= 1.67 (ASD)



0.90 (LRFD)

0.90 (LSD)

where S

is the elastic section modulus of the effective section

calculated relative to extreme compression ﬁber at F

and F

shall be determined as follows: For F

≥ 2.78F

,the member

segment is not subject to lateral-torsional buckling at bending

moments less than or equal to M

. The available ﬂexural

strength [moment resistance] shall be determined in accordance

with Section 4.2.2.1.

For 2.78F

> 0.56F



1 −

10F

36F



(4.64a)

For F

≤ 0.56F

= F

(4.64b)

where F

is the design yield stress as determined in accordance

with Section 2.2 and F

is the elastic critical lateral–torsional

buckling stress calculated in accordance with (a) or (b):

(a) For singly, doubly, and point-symmetric sections:

i. For bending about the symmetry axis:

⎧

⎪

⎨

⎪

⎩

√

for singly and doubly

symmetric sections (4.65a)

√

for point - symmetric

sections (4.65b)

12.5M

max

2.5M

max

+3M

+4M

+3M

(4.66)

where M

max

= absolute value of maximum moment in

unbraced segment

= absolute value of moment at quarter

point of unbraced segment

= absolute value of moment at centerline

of unbraced segment

= absolute value of moment at

three-quarter point of unbraced segment

and C

shall be permitted to be conservatively taken as

unity for all cases. For cantilevers or overhangs where

the free end is unbraced, C

shall be taken as unity. The

polar radius of gyration of the cross section about the

shear center is given as



+ r

+ x

where r

= radii of gyration of cross section about

centroidal principal axes

= distance from shear center to centroid

along principal x axis, taken as negative

Here A is the full unreduced cross-sectional area, S

the elastic section modulus of the full unreduced section

relative to the extreme compression ﬁber, and

)

(4.67)

where E = modulus of elasticity of steel

= effective length factors for bending about y

axis

= unbraced length of member for bending

about y axis

and



GJ +

(

)



(4.68)

where G = shear modulus

J = St. Venant torsion constant of cross section

= torsional warping constant of cross section

= effective length factors for twisting

= unbraced length of member for twisting

For singly symmetric sections, t he x axis shall be the

axis of symmetry oriented such that the shear center has

a negative x coordinate.

For point-symmetric sections, such as Z-sections, the

x axis shall be the centroidal axis perpendicular to the

web.

Alternatively, F

shall be permitted to be calcu-

lated using the equation given in (b) for doubly

symmetric I-sections, singly symmetric C-sections, or

point-symmetric Z-sections.

ii. For singly symmetric sections bending about the

centroidal axis perpendicular to the axis of symmetry,

Aσ



j + C



+ r

(

/σ

)



(4.69)

where C

equals +1 for the moment causing compres-

sion on the shear center side of the centroid and -1 for

the moment causing tension on the shear center side of

the centroid and

(

)

(4.70)

where K

= effective length f actors for bending about x

axis

= unbraced length of member for bending

about x axis

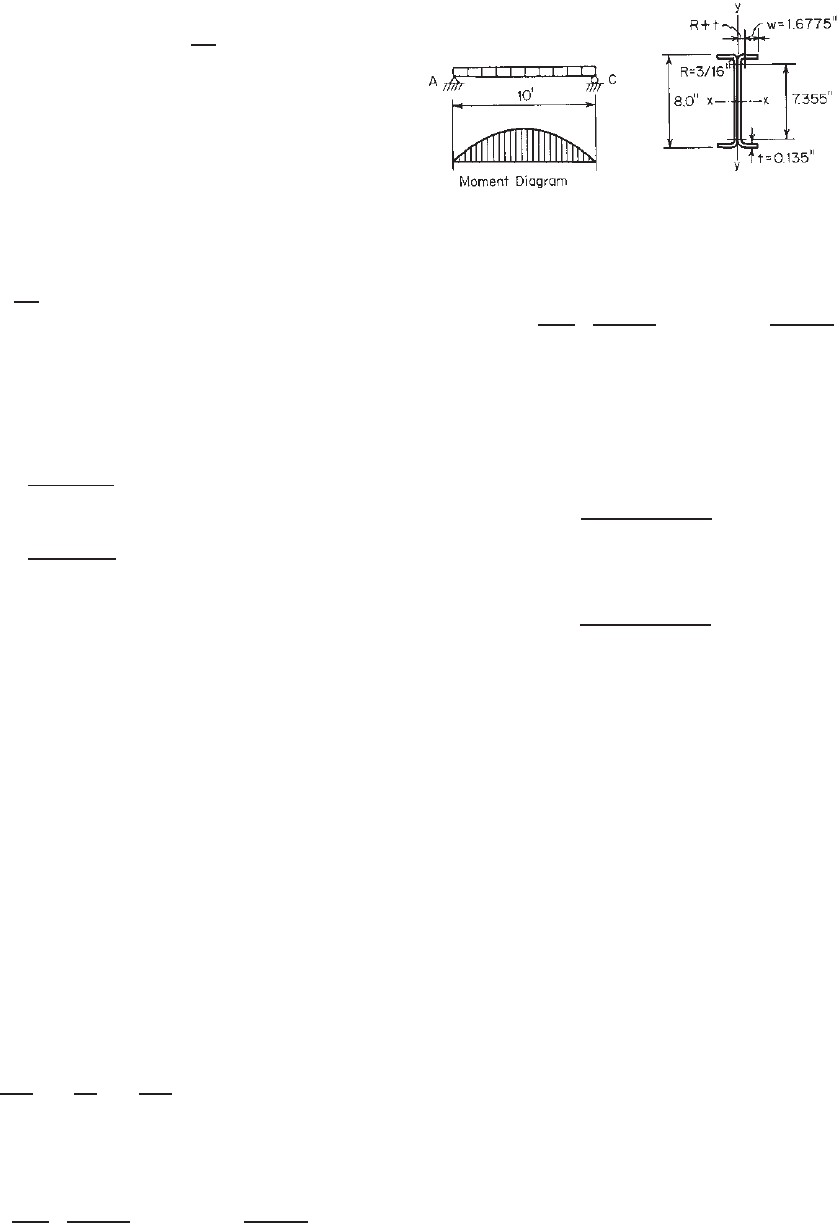
130 4 FLEXURAL MEMBERS

and

= 0.6 − 0.4





(4.71)

where M

and M

are the smaller and larger bending

moments, respectively, at the ends of the unbraced

length in the plane of bending; M

, the ratio of end

moments, is positive when M

and M

have the same

sign (reverse-curvature bending) and negative when they

are of opposite sign (single-curvature bending). When the

bending moment at any point within an unbraced length

is larger than that at both ends of this length, C

shall

be taken as unity,

j =





dA +





− x

(4.72)

(b) For I-sections, singly symmetric C-sections, or Z-sections

bent about the centroidal axis perpendicular to the web (x

axis), the following equations shall be permitted to be used

in lieu of (a) to calculate Fe:

⎧

⎪

⎨

⎪

⎩

for doubly symmetric

I - sections and

EdI

)

singly symmetric

C - sections (4.73a)

EdI

)

for point - symmetric

Z - sections (4.73b)

where d = depth of section

= moment of inertia of compression portion of

section about centroidal axis of entire section

parallel to web using full unreduced section

See (a) for deﬁnition of other variables.

According to Section C3.1.2.1 of the 2007 North Amer-

ican Speciﬁcation, it can be seen that for members bent

about the centroidal axis perpendicular to the web calcu-

lation of lateral–torsional buckling strength is unnecessary

when the unbraced length does not exceed a length, L

which is determined for M

= 2.78M

(or F

= 2.78F

)

(see Fig. 4.28). The following equations are given in

Section 1.4 of Part II of the AISI Design Manual

1..349

for

computing L

(a) For singly, doubly, and point-symmetric sections,

⎧

⎨

⎩









0.5

⎫

⎬

⎭

0.5

(4.74)

where

1. For singly and doubly symmetric sections,

7.72



πr



)

Figure 4.29 Example 4.9.

2. For point-symmetric sections,

30.9



πr



)

(b) For I-, C-, or Z-sections bent about the centroidal axis

perpendicular to the web (x axis), in lieu of (a), the

following equations may be used:

1. For doubly symmetric I-sections and singly

symmetric C-sections,



0.36C

EdI







0.5

(4.75a)

2. For point-symmetric Z-sections,



0.18C

EdI







0.5

(4.75b)

In addition, Part II of the Design Manual provides

beam design charts for determining the nominal ﬂexural

strengths of C-sections and Z-sections with lips. These

charts were prepared for F

= 33, 50 and 55 ksi (228, 345,

and 379 MPa; 2.32, 3.52, and 3.87 × 10

kg/cm

) with

= 1.0. The torsional unbraced length (K

) is assumed

to be equal to the unbraced length about the y axis (K

Example 4.9 For the I-beam used in Example 4.1, what is

the maximum spacing of lateral supports in order to use the

nominal moment of 312.35 in.-kips determined for section

strength? Assume that the I-section is to be used as a simply

supported beam with a span length of 10 ft to support a

uniform load (see Fig. 4.29).

SOLUTION. In order to use the nominal moment for

section strength, the maximum spacing of lateral s upports

can be determined from the following equation:

for section strength = M

for lateral–torsional

buckling strength

From Eqs. (4.4) and (4.63),

= S

BENDING STRENGTH AND DEFLECTION 131

As shown in Fig. 4.28, when K

≤ L

, M

= M

(or

= F

)andS

= S

. Assume that the elastic critical

lateral–torsional buckling stress of the I-section is deter-

mined according to Section C3.1.2.1(b) of the North Amer-

ican speciﬁcation. For F

= F

≥ 2.78F

Substituting Eq. (4.73a) for F

into the above expression

yields

)

≥ 2.78F

Therefore,

≤



/(2.78S

)

where E = 29.5 × 10

ksi

= 1.0 (assumed value)

d = 8.0 in.

= 50 ksi

= 1.0

= 0.724 in.

(see the following calculation)

Area A Distance from Ax

Element (in.

) y Axis, x (in.) (in.

)

Flanges 4(1.6775)(0.135) = 0.9059 1.1613 1.2217

Corners 4(0.05407) = 0.2163 0.1564 0.0053

Webs 2(7.355)(0.135) =

1.9859 0.0675 0.0090

Total 3.1081 1.2360

ﬂanges

= 4 ×

×0.135(1.6775)

=0.2124

= 1.4484 in.

= 0.724 in.

= 6.54 in.

(see the following calculation)

Area A Distance from Ay

Element (in.

) Mid depth y(in.) (in.

)

Flanges 4(1.6775)(0.135) = 0.9059 3.9325 14.0093

Corners 4(0.05407) = 0.2163 3.8436 3.1955

Webs 2(7.355)(0.135) =

1.9859 0 0

Total 3.1081 17.2048

web

= 2 ×

× (0.135)(7.355)

8.9522

= 26.1570 in.

8/2

= 6.54 in.

The maximum unbraced length between lateral

supports is



(29,500)(1)(8)(0.724)

2.78(6.54)(50)

= 43.1in.

Alternatively, the above unbraced length can be calculated

directly from Eq. (4.75a). Actually, the beam may be braced

laterally at one-third span length with an unbraced length of

Figure 4.30 Lateral supports.

Figure 4.31 Example 4 .10.

40 in., as shown in Fig. 4.30. For segment CD, C

= 1.01,

which is practically the same as the assumed value of 1.0.

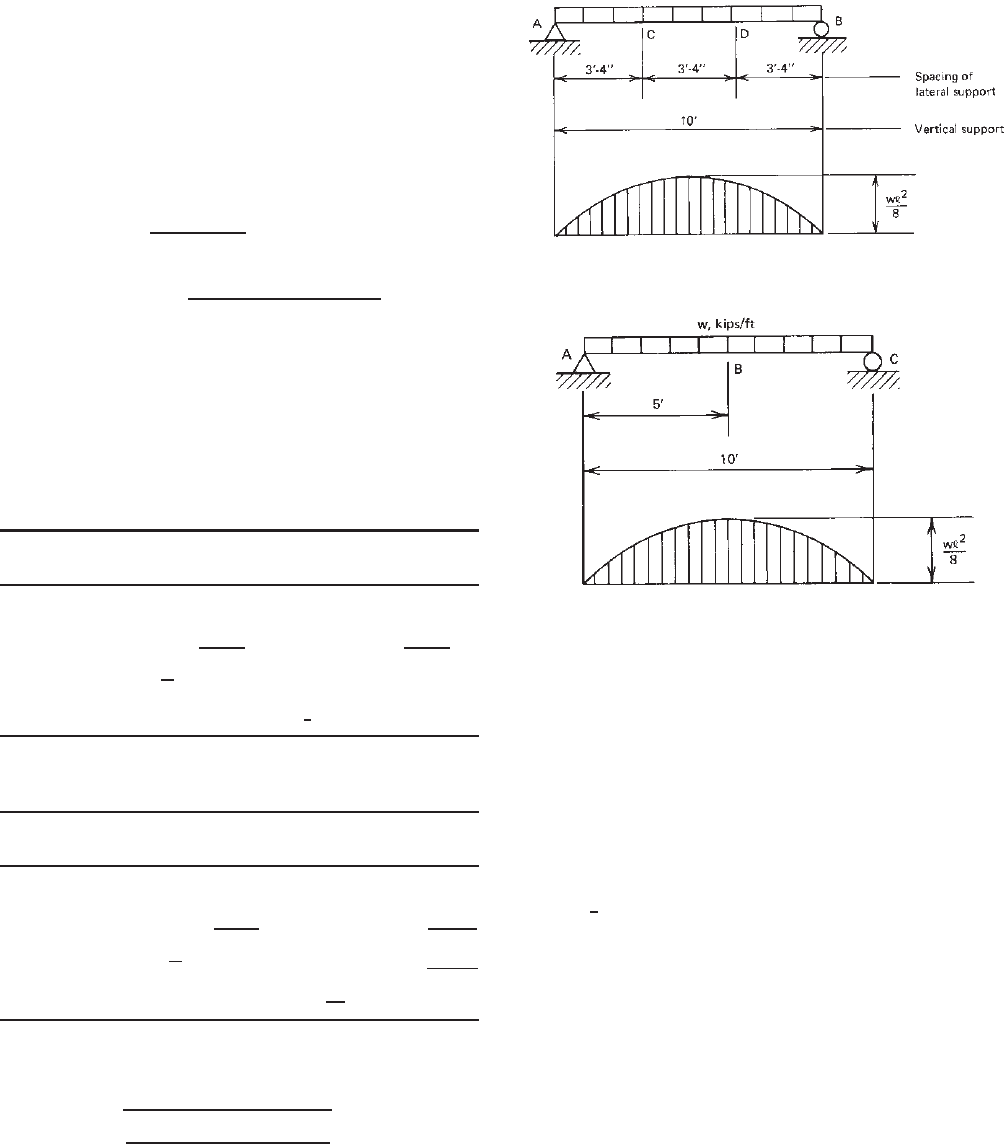
Example 4.10 Determine the allowable uniform load if

the I-beam used in Example 4.9 is braced laterally at both

ends and midspan. See Fig. 4.31. Use the value of C

determined by the formula included in the North American

Speciﬁcation and F

= 50 ksi. Use the ASD method and the

LRFD method with an assumed dead load–live load ratio

D/L =

SOLUTION

A. ASD Method

1. Nominal Moment for Section Strength. From Example

4.1, the nominal moment for section strength

according to Eq. (4.4) is

)

= S

= 312.35 in.-kips

2. Nominal Moment for Lateral–Torsional Buckling

Strength. From Example 4.9, S

= 6.54 in.

and

= 0.724 in.

Considering the lateral supports at

both ends and midspan and the moment diagram

shown in Fig 4.31, the bending coefﬁcient C

for

132 4 FLEXURAL MEMBERS

segment AB can be calculated by using Eq. (4.66) as

follows:

12.5M

max

2.5M

max

+ 3M

+ 4M

+ 3M

where M

max

= wL

/8 at midspan

= 7wL

/128 at

point of unbraced

segment

= 12wL

/128 at midpoint of unbraced

segment

= 15wL

/128 at

point of unbraced

segment

12.5(wL

/8)

2.5(wL

/8) + 3(7wL

/128)

+4(12wL

/128) + 3(15wL

/128)

= 1.30

Using Eq. (4.73a), with K

= 1.0,

)

(29,500)(1.30)(8)(0.724)

(6.54)

(

5 × 12

)

= 93.11 ksi

0.56F

= 28.00 ksi

2.78F

= 139.00 ksi

Since 2.78F

> 0.56F

, from Eq. (4.64a)



1 −

10F

36F



(

)



1 −

(

50.0

)

(

93.11

)



= 47.27 ksi

Based on Eq. (4.63), the nominal moment for lateral–

torsional buckling strength is

)

= S

in which S

is the elastic section modulus of the

effective section calculated at a compressive stress of

f = 47.27 ksi. By using the procedure illustrated in

Example 4.1, S

= 6.294 in.

Therefore, the nominal

moment for lateral–torsional buckling strength is

)

= (6.294)(47.27) = 297.5in.-kips

3. Allowable Uniform Load. Because (M

)

<(M

)

lateral–torsional buckling strength governs the design.

Use M

= 297.5 in.-kips to determine the allowable

moment as follows:



297.5

1.67

= 178.14 in.-kips

The maximum moment at midspan is wL

/8 ft-kips:

(

)

= 178.14 in.-kips

Then the allowable uniform load is

w = 1.188 kips/ft

It should be noted that the allowable load computed

above is based on the bending moment. It should also

be checked for shear, web crippling, deﬂection, and

other requirements as applicable.

B. LRFD Method.

Using the same method employed above for the ASD

method, the governing nominal moment for lateral–

torsional buckling strength is

= 297.5in.-kips

Since the I-section has an unstiffened ﬂange, the resistance

factor as listed in Table 3.1 and discussed in Section 4.2.1

is 0.90.

Therefore, the design moment is

= 0.90(297.5) = 267.75 in.-kips

Based on the load combination of Eq. (3.5a), the required

moment is

= 1.4M

where M

is the bending moment due to dead load.

Similarly, based on the load combination of Eq. (3.5b),

the required moment is

= 1.2M

+ 1.6M

= 1.2M

+ 1.6(5M

) = 9.2M

where M

is the bending moment due to live load. A

comparison of the above computations indicates that for a

given member the load combination of Eq. (3.5b) allows

a smaller moment M

than the load combination of

Eq. (3.5a). Therefore, the bending moment M

can be

computed from M

= φ

as follows:

9.2M

= 267.75 in.-kips

Therefore,

267.75

9.2

= 29.10 in.-kips

= 5M

= 145.50 in-kips

Theallowablemomentis

= M

+ M

= 29.10 + 145.50 = 174.60 in.-kips

The allowable uniform load can be calculated as follows:

(

)

= 174.60 in-kips w = 1.164 kips/ft

It can be seen that the allowable uniform load computed

on the basis of the LRFD method is similar to that computed

from the ASD method. The difference is only about 2%.

BENDING STRENGTH AND DEFLECTION 133

Figure 4.32 Example 4 .11.

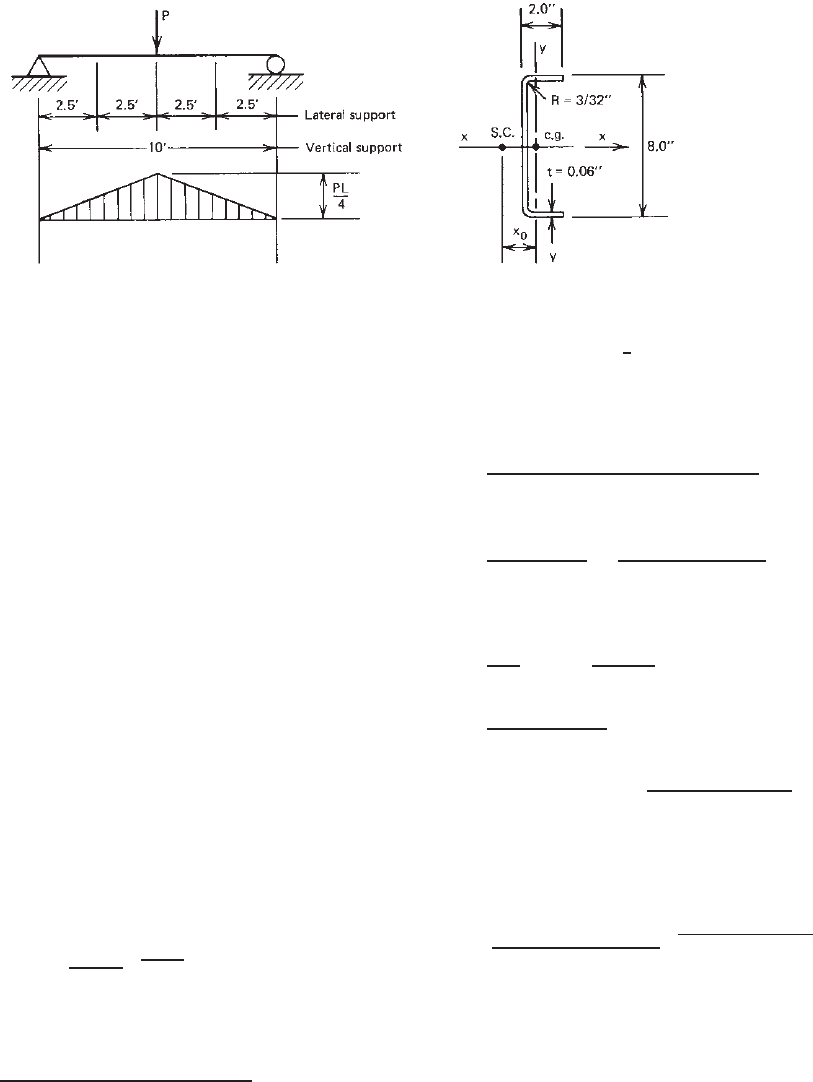
Example 4.11 For the singly symmetric channel section

(8 × 2 × 0.06 in.) shown in Fig. 4.32, determine the

nominal moment for lateral–torsional buckling strength

according to Section C 3.1.2.1 of the 2007 edition of the

North American Speciﬁcation. Assume that the channel is

used as a simply supported beam to support a concentrated

load at midspan and lateral supports are located at one-

fourth of the span length. Use F

= 33 ksi, K

= K

2.5ft.

SOLUTION

1. Sectional Properties. By using the design formulas

given in Part I of the AISI design manual, the

following full-section properties can be calculated:

A = 0.706 in.

=−0.929 in.

= 1.532 in.

= 3.14 in.

= 2.945 in. J = 0.000848 in.

= 0.569 in. C

= 2.66 in.

2. Elastic Critical Lateral–Torsional Buckling Stress, F

Because the given singly symmetric channel section is

subject to a moment bending about the symmetry axis

(x axis), the elastic critical lateral–torsional buckling

stress can be determined according to Eq. (4.65a) as

follows:

√

For two central segments, the value of C

can be

computed from Eq. (4.66) as follows:

12.5M

max

2.5M

max

+ 3M

+ 4M

+ 3M

where M

max

= PL/4 at midspan

= 5PL/32 at

point of unbraced

segment

= 6PL/32 at midpoint of unbraced

segment

= 7PL/32 at

point of unbraced

segment

Then

12.5(P L/4)

2.5(P L/4) + 3(5PL/32)

+4(6PL/32) + 3(7PL/32)

= 1.25





(

29,500

)

(

2.5 × 12/0.569

)

= 104.74 ksi



GJ +

(

)



(0.706)(3.14)



(11,300)(0.000848)

(29,500)(2.66)

(2.5 × 12)



= 125.0ksi

Therefore, the e lastic critical lateral–torsional buck-

ling stress is

(

1.25

)(

3.14

)(

0.706

)

(

1.532

)



(

104.74

)(

125.0

)

= 206.96 ksi

3. Critical Lateral–Torsional Buckling Stress, F

0.56F

= 18.48 ksi 2.78F

= 91.74 ksi

Since F

> 2.78 F

, the member segment is not

subject to lateral–torsional buckling. The nominal

moment should be determined in accordance with

Section 4.2.2.1 in this volume or C3.1.1(a) of the

Speciﬁcation:

= F

134 4 FLEXURAL MEMBERS

4. Nominal Moment M

.AccordingtoSection4.2.2.1

the nominal moment based on section strength can be

calculated a s follows:

= S

By using the same procedure illustrated in Example

4.1 w ith f = F

, the elastic section modulus of the

effective section is

= 1.211 in.

Therefore, the nominal moment is

= (1.211)(33) = 39.96 in.-kips

5. It should be noted that the above calculation is based

on Section C3.1.2.1(a) of the AISI North American

Speciﬁcation.

1.345

If Section C3.1.2.1(b) is used to

compute F

, then, according to Eq. (4.73a),

)

(

29,500

)(

1.25

)(

8.0

)(

0.1145

)

(

1.532

)(

2.5 × 12

)

= 241.78 ksi

Since F

> 2.78F

= 91.74 ksi, similar to Item 4

above, the compressive stress is

f = F

= 33 ksi

The elastic section modulus of the effective section is

= 1.211 in.

The nominal moment is

= 39.96 in.-kips

It can be seen that for the given channel section

with quarter-point lateral supports, Sections C3.1.2.1(a)

and C3.1.2.1(b) of the North American Speciﬁcation give

the same nominal moment for lateral–torsional buckling

strength.

4.2.3.4 Closed-Box Sections Closed sections such as

box shapes have relatively larger torsional stiffness as

compared with open sections such as I-beams, C-sections,

and Z-sections discussed in Sections 4.2.3.1 and 4.2.3.2. As

far as lateral–torsional buckling is concerned, these closed,

double-web sections are more stable than single-web open

sections, and therefore any use of closed-box sections will

result in an economical design if lateral–torsional stability

of the beam is essential.

In Ref. 4.18, Winter indicated that for closed-box beams

the bending strength is unaffected by lateral–torsional buck-

ling even when the length-to-width ratio is as high as 100

for a steel having a yield stress of 33 ksi (228 MPa or 2320

kg/cm

Previous editions of the AISI Speciﬁcation contained

in Section D3.3a conservative design provision for

lateral–torsional buckling of closed-box beams, in which

laterally unbraced box sections can be designed without

any strength reduction for lateral–torsional buckling

consideration if the ratio of the unsupported length to the

distance between the webs of the section does not exceed

0.086E/F

. In 1999, this design requirement was replaced

by Section C3.1.2.2 in the Supplement to the 1996 edition

of the AISI Speciﬁcation.

1.333

The same design provisions

are retained in the North American Speciﬁcation, except

that the laterally unbraced length, L, was clariﬁed to be

For a closed-box section subjected to a uniform bending

moment as shown in Fig. 4.23, the elastic critical moment

for lateral–torsional buckling is

3.84

(

)



All terms are deﬁned in Section 4.2.3.1, except that the

torsional constant J maybedeterminedbythefollowing

equation for a closed-box section having a uniform

thickness

4.157

J =

b + d

where b = midline or centerline dimension of ﬂange

d = midline or centerline dimension of web

t = wall thickness

When a closed-box section is subject to a nonuniform

bending moment, the above equation for the elastic critical

moment can be modiﬁed by a bending coefﬁcient C

follows:

(

)



GJ (4.76)

Consequently, the elastic critical lateral–torsional buck-

ling stress F

can be determined by Eq. (4.77) as given in

Section C3.1.2.2 of the 2007 edition of the North American

Speciﬁcation as follows

1.345



GJ (4.77)

in which S

is the elastic section modulus of the full unre-

duced section relative to the extreme compression ﬂange,

is the effective length factor, and L

is the unbraced

length for bending about y axis.

Based on Eq. (4.77), the following equation for L

can

be derived from F

= 2.78F

0.36C



GJ (4.78)