Арутюнян Е., Левитас Г. Занимательная математика. 1-5 классы
Подождите немного. Документ загружается.


Глава первая.
н
а
m
урал
ыеe
u
ела
Вообще:
вычесть а из Ь - значит найти число, которое
в
сумме с а дает Ь;
разделить а на Ь значит найти число, которое
в произведении с Ь дает а.
Но это значит, что нельзя делить на нуль. И в са
мом деле, попробуем разделить на нуль число 8. Если
бы при этом получилось какое-нибудь число а, то мы
могли бы записать: 8 : О
=
а, а значит, а· 0
=
8. Но это
неверно, так как а· О равно нулю, а вовсе не восьми.
Значит, никакого результата деление числа 8 на нуль
дать не может. Если бы вместо числа 8 мы взяли лю
бое другое число (кроме нуля!), получилось бы то же
самое. Значит, никакое число, не равное нулю, разде
лить на нуль нельзя. А можно ли нуль разделить на
нуль? Если бы это было возможно, то мы могли бы
найти результат такого деления -какое-то число а.
Но в том-то и дело, что если О: О
=
а, то а· 0
=
о. А это
верно для любого числа а! Значит, результатом деле
ния нуля на нуль могло бы быть любое число. Поэто
му найти этот результат нельзя. Этим и объясняется
всем известное правило:
НИКАКОЕ ЧИСЛО НЕЛЬЗЯ ДЕЛИТЬ НА НУЛЫ
Число, которое делят, называется делимым. Чис
ло, на которое делят, называется делителем. Число,
которое получается в результате деления, называется
частным .
При делении небольших чисел можно пользовать
ся все той же таблицей умножения.
Все при меры на деление, которые можно получить
из таблицы умножения однозначных чисел, надо
знать наизусть. Получаются эти примеры так: внутри
таблицы берем какое-нибудь число - это делимое;
121
Г
лава
первая
. Натур
аль
ые числ
а
делителем может быть номер строки, в которой стоит
это число (тогда частное - номер столбца), или номер
столбца (тогда частное - номер строки).
.
1
2
3
4
1
1
2
3
4
2 2
4
6
8
3
3
6
9
12
4
4
8
12 16
5
5
10
15
20
6 6
12
18
24
7
7
14
21
28
8 8
16
24 32
9
9
18
27
36
5
6
7
5
6
7
10
12
14
15
18
21
20
24
28
25
30
35
30
36
42
35
42
49
40
48
56
45
54
63
8
8
16
24
32
40
48
56
64
72
9
9
18
27
36
45
54
63
72
81
Вот сразу два
примера:
35 : 7 = 5
35 : 5 = 7
Многозначные числа делят углом. Как это делает
ся, покажем на примере. Разделим 3638 на 34.
Запишем эти числа так:
3638 �
Деление, в отличие от сложения, вычитания и ум
ножения, начинают не справа, а слева. В числе 3638
первая цифра делимого 3 обозначает число, в котором
делитель 34 не помещается ни одного раза. Поэтому
возьмем две цифры слева: 3 и 6. Они образуют число
36. В нем делитель 34 помещается один раз. Запишем
в частном число 1:
3638 �
1
Умножим 34 на 1 и подпишем результат под чис
лом 36:
122
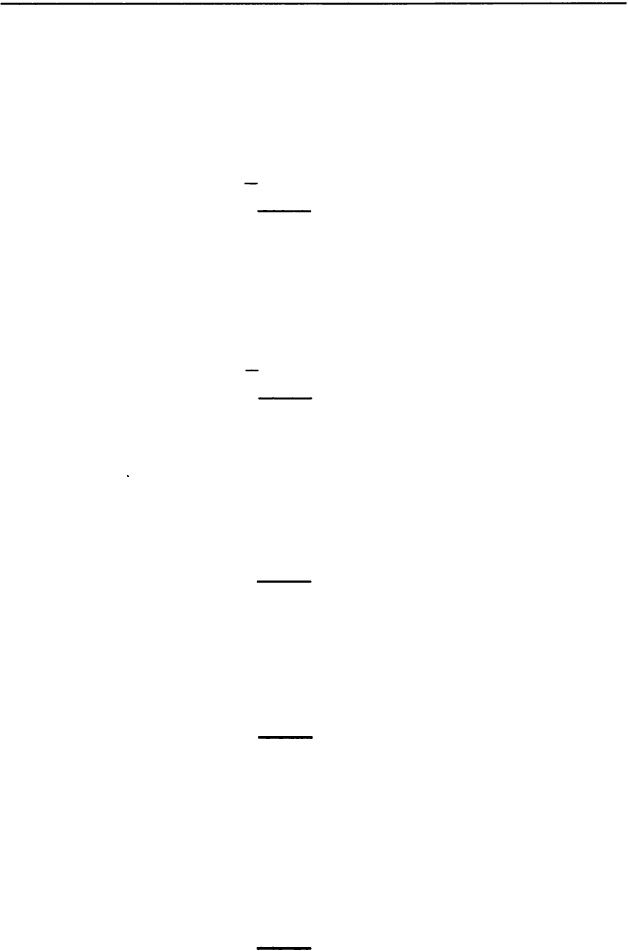
Г
лава
первая.
Натураль
кые числ
а
Вычтем 34 из 36:
3638 �
34
1
3638
�
34
1
2
Продолжаем деление. Для этого снесем следую
щую цифру 3:
3638
�
34
1
23
В числе 23 делитель 34 не помещается ни разу. Ста
вим в частном нуль:
_
3638
�
34
10
23
Сносим последнюю цифру 8
:
_
3638
�
34
10
238
в числе 238 делитель 34 помещается 7 раз, что
нетрудно установить, умножая число 34 на 1, на 2
и так далее. Записываем число 7 в частное:
_
3638
�
34
107
238
123
Глава первая. Натуральые ч
u
сла
Умножаем 34 на 7 и подписываем результат
п
од
числом 238
:
3638
34
107
238
238
Вычитаем полученное число из 238:
_
3638
34
107
238
238
О
Деление окончено. Ответ: 107. Для проверки мож
но пере множить 107 и 34. Получится 3638.
Какие бы натуральные числа мы ни взяли, всегда
можно их сложить, вычесть (из большего меньшее),
перемножить. А вот разделить одно из этих чисел
(даже большее на меньшее) удается не всегда. Возьми
14 конфет и попробуй разделить их между тремя
людьми поровну . Каждый получит по 4 конфеты,
но еще 2 конфеты останутся:
13
14
10
11
12
7
8
9
4
5
6
1
2
3
Математики говорят, что число 14 делится на чис
ло 3 с остатком. Это можно записать так:
14 : 3 = 4 (ост. 2).
124
Глава первая. На
m
уральые
u
сла
Здесь 14 по-прежнему называется делимым, 3 -
делителем, а 4 называется неполным частным. Если
в при мере 3638 : 34 увеличить делимое на единицу,
то получится пример деления с остатком:
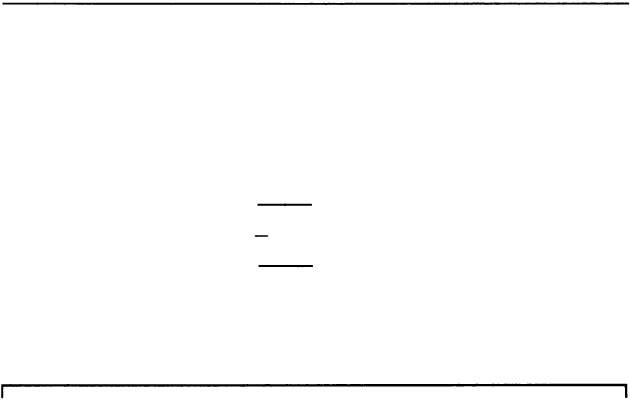
_
3639 �
34
107
239
238
1
3639 : 34 = 107 (ост. 1).
Задачи
1. Найди частное, пользуясь таблицей умножения:
36 : 9; 48 : 6;
54 : 9; 56 : 7;
360 : 9; 480 : 8; 540 : 60;
5600 : 8.
2. Два числа перемножили - получилось 25. По
том большее из этих чисел разделили на меньшее -
опять 25. Что это за числа?
3. Существует ли такое число, которое делится
на все остальные числа? Существует ли такое число,
на которое делятся все числа?
4. Расставь между числами 9 9 9 9 знаки действий
так, чтобы получилось 100.
5. То же для чисел 5 5 5 5.
6. Семь одинаковых батонов хлеба надо разделить
поровну между двенадцатью людьми. Как это сде
лать, разрезая каждый из батонов на равные части,
но не разрезая ни один на 12 частей?
7. В коробке лежат 15 шариков: черных, белых
и красных. Красных шариков в 7 раз больше, чем
белых.
Сколько в коробке черных шариков?
125
Глава первая. Натуралькые числа
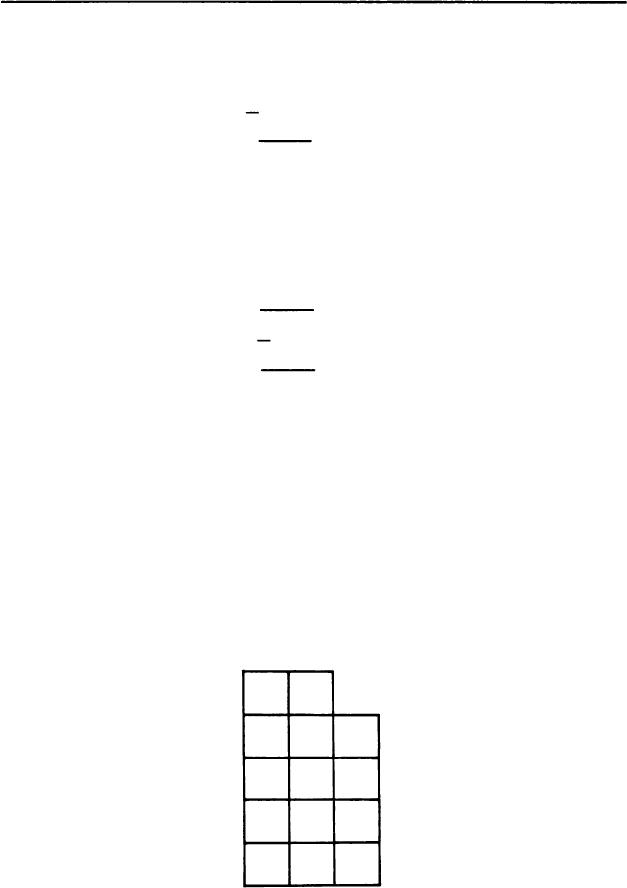
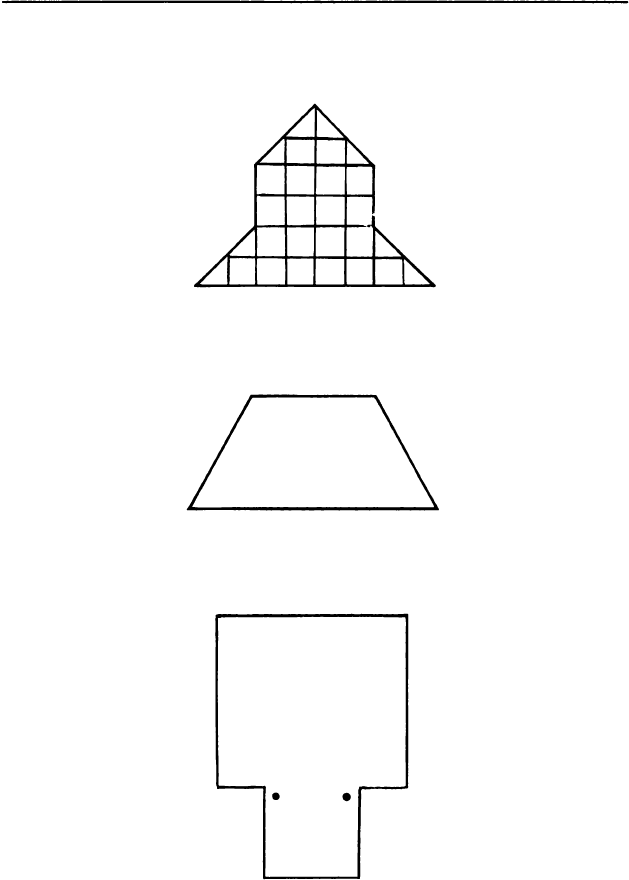
8. Как разрезать эту фигурку на четыре одинако
вых четырехугольника?
9. Как разрезать на четыре одинаковых четырех
угольника эту фигуру?
/
10. А как разрезать эту пластинку на шесть одина
ковых частей?
• • • • • • • •
• ••• ••••
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
• •
•
• •
•
•
•
•
•
•
•
•
•
•
•
•
•
•
• •
•
•
•
�.
•
•
. -
•
•
•
•
•
•
• •
•
•
••
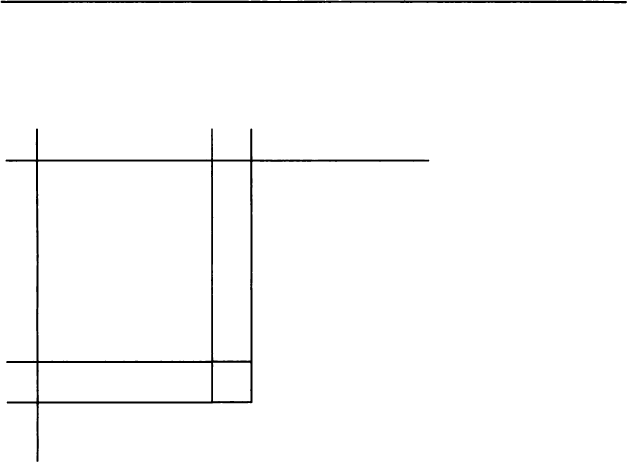
11. Как разделить этот участок земли на пять
одинаковых квадратов? А можно ли разделить его
на четыре равных участка?
126
Глава первая. Натуральные ч
u
сла
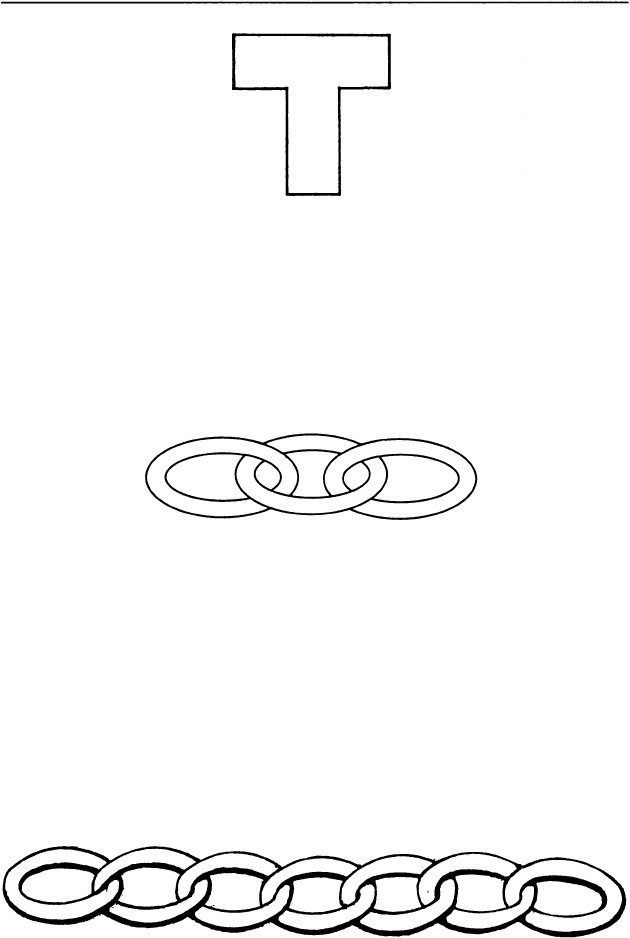
12. Здесь нарисована цепочка из трех бумажных ко
лечек. Если разрезать среднее колечко, она распадется
на три части. Как составить цепочку из трех колечек,
чтобы она распадась на три части при разрезании лю
бого колечка? А можно ли составить цепочку из пяти
колечек так, чтобы она распадалась на пять частей
при разрезании любого колечка?
13. Постоялец гостиницы, не имея денег, догово
рился с хозяином, что будет расплачиваться, отдавая
ему каждый день одно из семи звеньев своей золотой
цепи. Но портить цепь, распиливая каждое звено, было
жалко, и они, поразмыслив, сообразили, что можно
распилить всего одно звено. И правда, распилив это
звено, они смогли устроить так, что у хозяина каж
дый день прибавлялось по одному звену цепи. Как
они этого добились?
127
Глава
первая. Нат
ураль
кые числ
а
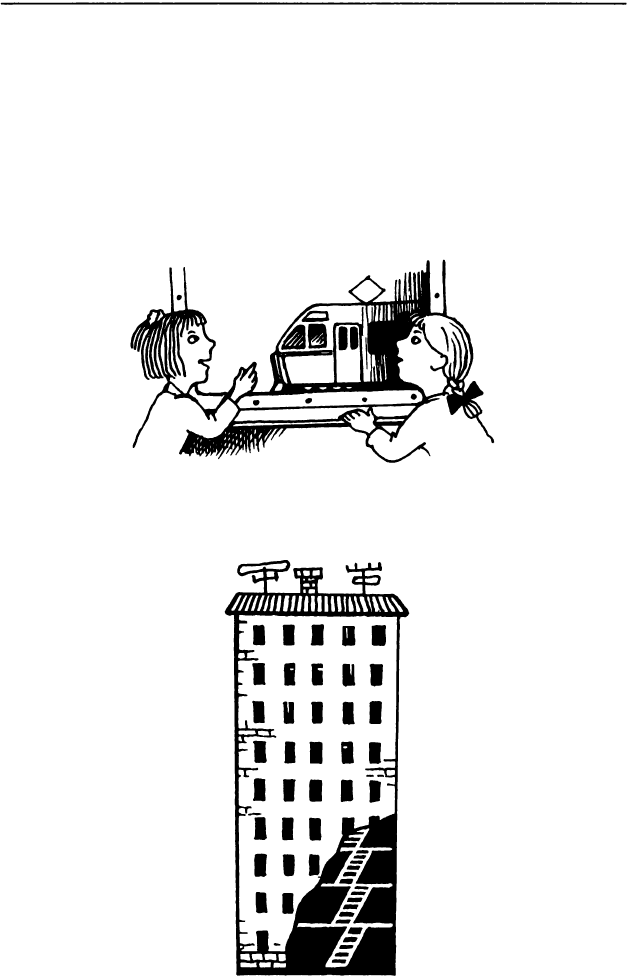
14. В вагоне электрички ехали из города на дачу
Соня и Ира.
- Посмотри, - сказала Ира, - обратные элект
рички нам встречаются через каждые 5 минут. Как
ты думаешь, сколько их прибывает в город за час?
- Конечно, 12, так как 60 : 5 = 12, - сказала
Соня.
Но Ира не согласилась с ней. Почему?
15. Во сколько раз путь на девятый этаж длиннее
пути на третий этаж того же дома?
128

Глава первая. На
m
уральые ч
u
сла
16. Петя нашел один гриб, Коля - два, а Паша
три. Мама дала им 18 орехов и попросила разделить
их по заслугам. Сколько орехов должен получить
каждый?
17. В другой раз Петя, Коля и Паша ловили рыбу.
Петя поймал трех плотвичек, Коля - пять. А Паша
не поймал ни одной рыбы. Когда стали варить уху,
Паша пообещал за это сделать вместо братьев восемь
домашних заданий по математике. Сколько домаш
них заданий он должен сделать вместо Пети и сколь
ко вместо Коли?
18. Летели галки, увидели палки. Если на каждую
палку сядет по галке, то для одной галки не хватит
палки. А если на каждую палку сядет по две галки,
то одна из палок останется без галок. Сколько было
галок? Сколько было палок?
5-22 129

Глава первая. Натуральные числа
19. А вот еще несколько числовых ребусов.
1
)
*
2
*
5
*
1
325
2)
_
***
I
*
***
1
**
*
3
***
*
0
**
*
9
**
*
5
*
*
5
*
О
3) ПИРОГ : И = гости
4
)
_
****
�
**
368
***
***
200
***
о
6) **234* : 72
= *0***.
7) ***1*
: 11 =
*9*.
8)
_
****
5
�
*
7
***
***
***
о
130
**
**
*
3
*
***
О
5)
****
**
.**
3
*
**
о
9)
*******
I
�
*
_
*
_
***
**
8
**
**
**
***
***
о
