Арутюнян Е., Левитас Г. Занимательная математика. 1-5 классы
Подождите немного. Документ загружается.


Глава
первая. Натуральые числа
17. Математиче
с
кий фокус. Дай товарищу две таб
лички и попроси написать на одной четное число, а на
другой - нечетное. Пусть он по секрету от тебя поло
жит одну табличку в левый карман, а другую - в пра
вый. Фокус состоит в том, что ты берешься угадать,
в каком кармане лежит четное, а в каком нечетное чис
ло. Для этого твой товарищ должен только умножить
на 2 содержимое левого кармана и прибавить к резуль
тату содержимое правого кармана. Если он сообщит
четный результат, значит, в левом кармане число не
четное, а если он сообщит нечетный результат, то в ле
вом кармане число четное. Объясни этот фокус.
18. Какое наименьшее число при делении на любое
число первого десятка дает остаток на 1 меньше, чем
делитель?
19. Если от задуманного трехзначного числа от
нять 7, то разность разделится на 7, если от того же
числа отнять 8, то оно разделится на 8, а если отнять
9
, оно разделится на 9. Какое число задумано?
20.
Если от трехзначного числа отнять 27,
оно раз
делится на 27, а если к нему прибавить 37, оно разде
лится на 37. Что это за число?
21. Зная, что 37· 3 = 111, найди 37· 27, не умно
жая в столбик.
22. Число 4876391520 интересно не только тем,
что в его записи использованы все 10 цифр, но и тем,
что оно делится на все числа от 1 до 18. Чтобы убе
диться в этом, достаточно проверить, что 4876391520
делится всего на семь чисел. Что это за числа?
151
Глава первая. Натуральые числа
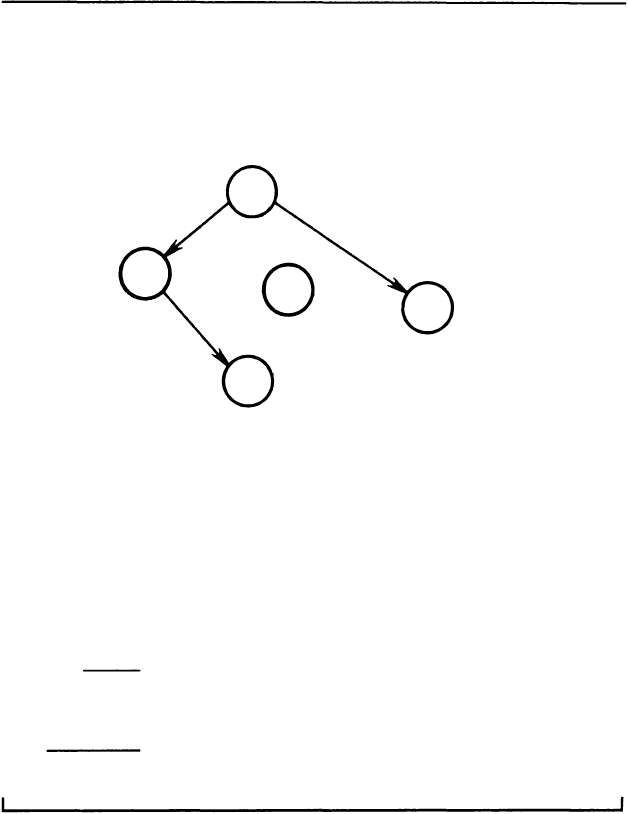
23. В кружочках написали числа 1, 2, 3, 4, 6 и 12
и от каждого числа провели стрелки ко всем его дели
телям. Но потом все числа и часть стрелок стерлись.
Как выглядела вся схема?
о
24. Проверь признак делимости трехзначного чис
ла на 8: на 8 делятся все те и только те трехзначные
числа, у которых двузначное число, образованное ци
фрами сотен и десятков, сложенное с половиной чис
л
а единиц, делится на 4.
25. Расшифруй ребус, в котором произведение
кратно 9:
4***
х ***
****
+
****
****
*****00
П
р
ос
т
ы
е
ч
исла
Можно ли записать в виде формулы, что число 350 де
лится на число 14? Чтобы это сделать, разделим 350
на 14:
152

Глава первая. На
m
уралькые
исла
350 : 14 = 25.
Это равенство можно переписать так:
350 = 14 ·25
Точно так же можно записать в виде формулы, что
число а делится на число Ь. Разделим а на Ь:
а: Ь = n, или
а
= Ьn.
у нас получилось, что если а делится на Ь, то суще
ствует такое натуральное число n, что а = Ьn. Конеч
но, можно было бы остановиться на записи а : Ь = n.
Формула а = Ьn полезна тем, что она выражает а че
р
ез
Ь - кратное через делитель.
Существует ли такое натуральное число, которое
не имеет ни одного делителя? Таких чисел нет: всякое
натуральное число делится само на себя, а значит,
имеет хотя бы один делитель - само себя: 11 имеет
делителем число 11, число 347 имеет делителем число
347.
Кроме того, каждое число имеет делителем число
1, так как на 1 делится любое число.
Из сказанного получается, что каждое натураль
ное число имеет два делителя: само себя и 1. Эти два
делителя могут совпадать - если само число равно 1.
у числа 1 только один делитель - число 1. Но любое
натуральное число, кроме 1, имеет хотя бы два дели
теля: само себя и единицу. Например, число 2 имеет
два делителя: 1 и 2, число 3 - два делителя: 1 и 3,
а вот число 4 имеет три делителя: 1, 2 и 4.
Натуральное число, которое имеет ровно два де
лителя, называется простым числом.
Натуральное число, которое имеет больше двух
делителей, называется составным числом.
153

Глава первая. Натуральые числа
Число 1 - не простое и не составное, так как у не
го всего один делитель.
Как узнать, простое или составное число 163? Для
этого надо выяснить, имеет ли 163 другие делители,
кроме чисел 1 и 163. Если такие делители имеются, то
они находятся среди чисел 2, 3, 4, 5, ... , 160, 161, 162,
так как 163 не может делиться на числа, большие,
чем оно само.
Проверять, делится ли 163 на каждое из всех этих
чисел, было бы слишком долго. Но оказывается, это
и не нужно. А достаточно сделать всего 5 проверок.
Сейчас мы убедимся в этом.
Самое маленькое число, на которое могло бы де
литься 163, - число 2. Но на 2 число 163 не делится
(его последняя цифра - нечетная).
Не может 163 делиться и ни на какое число, деляще
еся на 2, например на 42. Ведь если бы 163 делилось на
42, его можно было бы записать в виде: 163 = 42n.
Но 42 = 2·21, значит, было бы 163 = (2 · 21)n. А тогда
было бы 163 = 2(21n). Но это значило бы, что 163 рав
но произведению числа 2 на натуральное число 21n,
то есть 163 делится на 2, а это неверно.
Теперь ясно, что 163 не делится на четные числа:
на 2, 4, 6, 8, ... , 160, 162.
Вычеркнем эти числа из нашего списка.
Первое оставшееся в списке число - 3. 163 на 3
не делится (сумма его цифр равна 10). Но тогда оно
не делится ни на одно из чисел, делящихся на 3: на 3,
6, 9, ... , 156, 159, 162.
Вычеркнем эти числа из нашего списка.
Первое оставшееся в списке число - число 5. 163
не делится на 5 (его последняя цифра не делится на 5).
Значит, 163 не делится ни на одно число, делящееся
на 5. Вычеркнем из списка и эти числа.
Теперь в списке остались только такие числа:
154

Глава первая. Натуральные числа
7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53,
59, 61, 67, 71, 73, 77, 79, 83, 89, 91, 97, 101, 103, 107,
109, 113, 119, 121, 127, 131, 133, 137, 139, 143, 147,
149, 151, 157, 161.
Все остальные числа от 2 до 162 делятся либо на 2,
либо на 3, либо на 5.
Проверим делимость числа 163 на первое из остав
шихся чисел - на 7:
163 : 7 = 23 (ост. 2).
Итак, 163 на 7 не делится. Значит, не делится оно
и на любое число, делящееся на 7. Вычеркнем все эти
числа из списка.
Теперь проверим делимость 163 на первое оставше
еся число - на 11. 163 на 11 не делится (3 + 1 = 4,
6 - 4 = 2, 2 на 11 не делится). Поэтому 163 не делится
и на все числа, делящиеся на 11. И их вычеркнем.
В списке останутся: 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107,
109, 113, 127, 131, 137, 139, 147, 149, 151, 157.
Мы уже выполнили 5 про верок и установили, что
163 не делится на 2, на 3, на 5, на 7 и на 11.
Докажем, что проверять, делится ли 163 на остав
шиеся в списке числа, уже не надо. Подумаем, какое
число получилось бы в частном, если бы 163 раздели
лось на какое-нибудь из оставшихся чисел. Возьмем
самое маленькое из них - число 13. Тогда частное
должно быть меньше числа 13, потому что 13 ·13 уже
больше, чем 163. Но ни одно число, меньшее 13,
не является делителем числа 163 - мы это провери
ли. Тем более не стоит проверять числа, большие 13.
Значит, проведенные нами пять проверок доказы
вают, что число 163 не имеет никаких делителей,
кроме чисел 1 и 163. Число 163 - простое.
155

Глава первая. Натуралькые
"
исла
I
Задача.
Как с помощью двух проверок пока
з
ать,
что число 19 - простое? Как с помощью трех прове
рок показать, что число 47 - простое?
Простыми И составными числами очень интересо
вались в Древней Греции. Греческий математик Эра
тосфен, живший в Александрии (между прочим, он
заведовал там знаменитой библиотекой) в 111 веке
до нашей эры, придумал способ отыскания простых
чисел, которым пользуются до сих пор. Сейчас име
ются таблицы, содержащие многие тысячи простых
чисел. Эти таблицы составлены с помощью современ
ных компьютеров, но способ вылавливания простых
чисел остался тем же, какой был придуман Эратосфе
ном. Этот способ называется решетом Эратосфена. По
кажем его действие на при мере такой задачи: нужно
найти все простые числа в первой сотне.
Запишем все натуральные числа от 2 до 100. Чис
ло 1 не пишем, потому что оно не простое.
2 3
4 5
6
7
8
9
10
11
12
13
14
15
16
17
18 19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
П
ервый
шаг: число 2 - простое (у него ровно два
делителя: 1 и 2); все остальные числа,
кратные
двум,- составные; вычеркиваем их:
156

r
лава пе
р
вая. Натуральые числа
2 3
5
Ж
7
Z
9
11
13
М
15
17
19
�
21
Х
23
25
�
27
$
29
31
м
33
М
35
�
37
39
41
М
43
М
45
47
49
51
И
53
55
�
57
$
59
�
61
М
63
М
65
67
$
69
71
73
75
%
77
$
79
81
83
м
85
87
89
91
93
95
W
97
%
99
у нас остались следующие числа:
2
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
51
53 55
57
59
61 63
65
67
69
71
73
75
77
79
81
83 85
87
89
91
93
95
97
99
Втор
ой
ш
аг: первое из оставшихся чисел - число
3 - простое (оно не делится на меньшие числа, кроме
1, иначе мы бы его уже вычеркнули); все остальные
числа, кратные трем, - составные; вычеркиваем их:
2
3
5
7
А
11 13
%
17
19
%
23
25
Ж
29
31
35
37
41
43
47
49
Ж
53
55
М
59
61
65
67
157

Глава первая. Н
а
туралькые исла
71
73
%
77
79
М
83
85
М
89
91
95
97
У нас остались числа:
2 3
5
7
11
13
17
19
23
25
29
31
35
37
41
43
47
49
53
55
59
61
65
67
71
73
77
79
83
85
89
91 95 97
Третий
ш
аг: первое из оставшихся чисел - число
5 -простое (оно не делится на меньшие числа, кроме
1
, иначе мы бы его уже вычеркнули); все остальные
числа, кратные пяти, - составные; вычеркиваем их:
2
3
5
7
11
13
17 19
23
29
31
�
37
41
43
47
49
53
59
61
�
67
71
73
77
79
83
�
89
91
97
Остались числа:
2
3 5
7
11
13
17
19
23
29
158

Глава
первая.
Натуральые
числа
31
37
41
43
47
49
53
59
61
67
71 73
77
79
83
89
91
97
Четвертый
ш
аг: первое из оставшихся чисел -
число
7 - простое (оно не делится на меньшие
чис
ла, кроме 1, иначе мы бы его уже вычеркнули);
все
остальные числа, кратные семи, - составные; вы-
черкиваем их:
2 3 5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
r
79
83
89
М
97
Осталось:
2 3 5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
П
ятый
ш
аг: первое из оставшихся чисел -
число
11
- простое; все остальные
числа, кратные
одиннад-
159
r
лава пе
р
вая. Натуральн
ые
и
сла
цати,- составные. Посмотрим, остались ли у нас еще
невычеркнутые числа, кратные одиннадцати. В пер
вой сотне следующие числа кратны одиннадцати:
11 - простое число;
22 = 2
•
11 - вычеркнуто на первом шаге
(делится на 2);
33 = 3
•
11 - вычеркнуто на втором шаге
(делится на 3);
44 = 4
•
11 - вычеркнуто на первом шаге
(делится на 2);
55 = 5 ·11 - вычеркнуто на третьем шаге
(делится на 5);
66 = 6
•
11 - вычеркнуто на первом шаге
(делится на 2);
77 = 7
•
11 - вычеркнуто на четвертом шаге
(делится на 7);
88 = 8
•
11 - вычеркнуто на первом шаге
(делится на 2);
99 = 9 • 11 - вычеркнуто на втором шаге
(делится на 3).
Так что вычеркивать нам уже больше нечего. Пер
вое число, которое следовало бы вычеркнуть, - это
даже не 10 ·11 (все четные числа уже вычеркнуты),
а 11 ' 11, то есть 121. Но это число уже выходит из на
шего промежутка: 121 > 100.
Но у нас еще осталось очень много чисел, кроме 11.
Могут ли среди них быть составные? Предположим,
например, что число 83 - составное. Какие у него мо
гут быть делители? Если бы оно делилось на какое-ни
будь число, меньшее одиннадцати, мы бы его давно
вычеркнули. А если бы у него были только делители,
которые не меньше одиннадцати, оно само было бы не
меньше, чем 11 ' 11, то есть чем 121. Но 83 < 100 и тем
более 83 < 121. Значит, число 83 не может быть со
ставным, оно простое. И все числа, оставшиеся невы
черкнутыми, - простые.
160
