Арутюнян Е., Левитас Г. Занимательная математика. 1-5 классы
Подождите немного. Документ загружается.


Глава в
т
орая
. Д
ро
би
Дробь % равна частному а: Ь.
Недаром на любом микрокалькуляторе кнопка
«( деление»
выглядит так:
Дробная черта и двоеточие означают одно и то же
действие - деление.
Раз уж речь зашла о калькуляторе, обратим внима
ние на то, что на его дисплее мы никогда не увидим
никаких записей с дробной чертой. Калькулятор все
пишет в десятичной системе счисления: каждая циф
ра правее или левее других, но не выше и не ниже. Хо
чешь узнать, чему равна дробь l' - набираешь 3, на
жимаешь кнопку
«( деление» ,
набираешь 4, затем знак
равенства - и получаешь запись: 0.75. Так записыва
ет калькулятор десятичные дроби: он сообщает нам,
что три четверти равны нулю целых семидесяти пяти
сотым. Мы сразу получили запись дроби 1в виде деся
тичной дроби 0,75. Подробно об этом мы поговорим
позже. Точно так же можно узнать, чему равна дробь
!: набираем 4, деление, 2, знак равенства - и получа
ем 2. Естественно:
!
= 4 : 2 = 2.
Зная, что % = а : Ь, можно догадаться о некоторых
важных свойствах дробей: ведь свойства частных
нам известны! Например, от увеличения делимого в
несколько раз частное увеличивается во столько же
раз. Отсюда сразу следует, что от увеличения числи
теля в несколько раз дробь увеличивается во столько
же раз:
I
Y�%
·
k
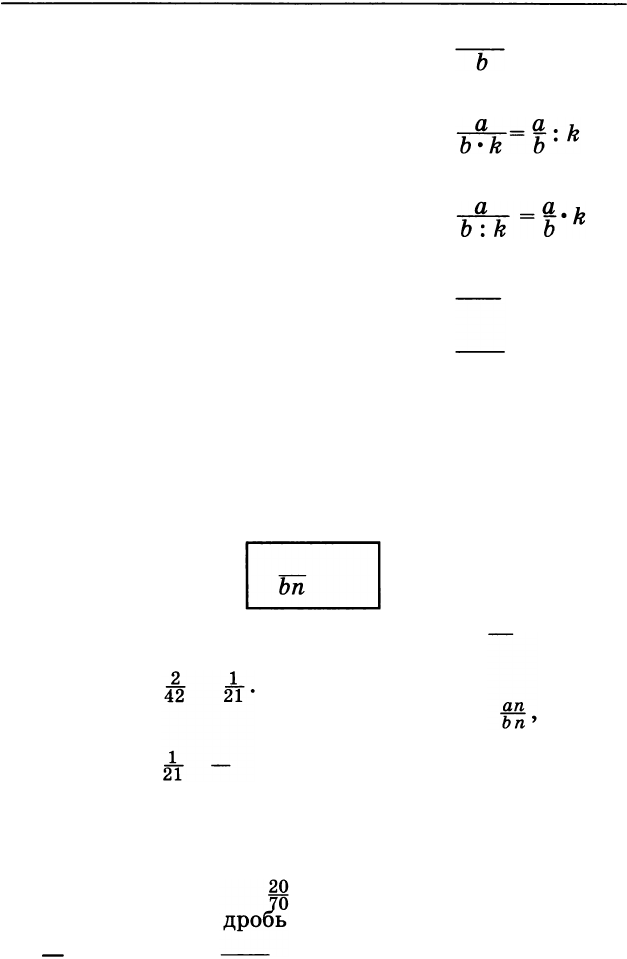
Каждому свойству частных соответствует свойство
дробей:
181
r
л
а
в
а вторая.
Д
роби
от уменьшения делимого в не
сколько раз частное уменьшается
во столько же раз;
от увеличения делителя в не
сколько раз частное уменьшается
во столько же раз;
от уменьшения делителя в не
сколько раз частное увеличивает
ся во столько же раз;
от увеличения или уменьше
ния в несколько раз и делимого, и
делителя частное не изменяется.
а
·
. k
а
=
-
ь
:
k
-
ь
-
а· k а
b·k
=
Ь
а
:
k_ а
Ь
:
k -Ь
Последнее получившееся у нас утверждение назы
вается
основным свойством дро
би
.
Повторим его еще раз:
От увеличения или уменьшения числителя и зна
MeHaTeля в одно и то же число раз значение дроби не
изменяется.
аn _а
Ьn
-о
Читая это равенство слева направо:
а
n
=
мы
Ь
n
Ь
'
делим числитель и знаменатель на одно и то же чис-
ло,
например
4
�
=
А
·
Читая это равенство справа налево: =
g�,
мы ум
ножаем числитель и знаменатель на одно и то же чис
ло, например
А
=
4
2
2
•
Основное свойство дроби позволяет иногда упро
щать дроби, деля числитель и знаменатель на одно и
то же число. Такая операция называется сокращени
ем дроби.
Например, у дроби j8
и числитель, и знаменатель
делится на 10. Эту
дробь
можно сократить на 10:
2
0
_
2
2
·
10 _
7
0
-
'
так как
7
·
10
-
7
·
182

Глава в
т
орая.
Д
роби
Д
ро
б
и
с
разн
ым
и
зна
ме
на
те
ля
м
и
Ну а как сравнивать, складывать, вычитать дроби
с разными знаменателями? Как, например, сложить
в старинной задаче «столько,
да полстолька, да чет
верть столька»
(то есть единицу, половину и чет
верть)? Или как догадаться, что две восьмых ноты и
одна четверть составляют полный такт в размере i:
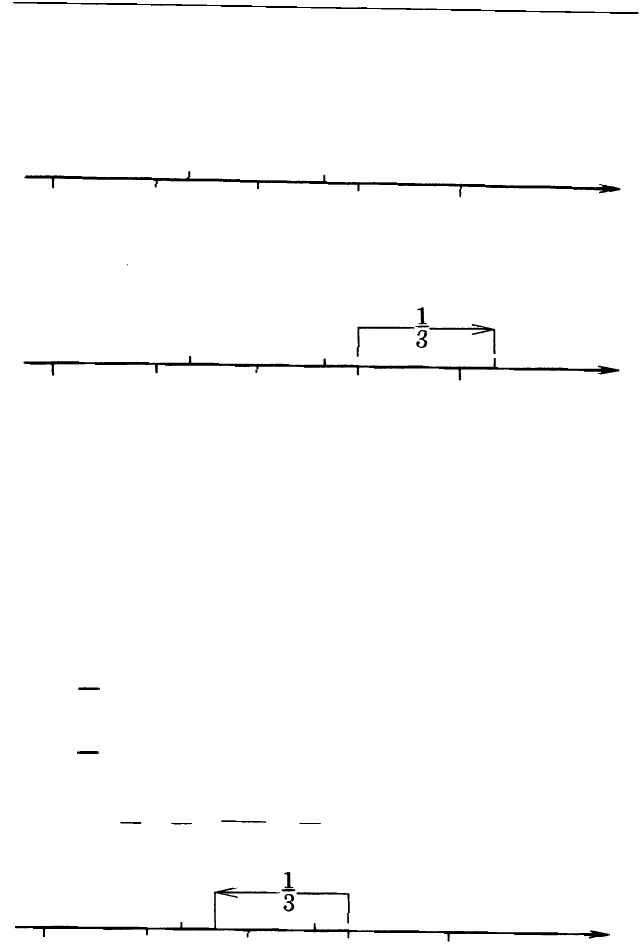
Одним способом это можно сделать наверняка -
с помощью числовой прямой. Сравним, сложим и
вычтем дроби ! и !.
I
»
4
Глава в
т
орая.
Д
ро
би
Попробуем теперь проделать то же самое с дробями
1
3
З
И
4
·
1) Сравнение.
1
3
I
о
В
1 3
И
Д
Н
О
, что
3
<
4
·
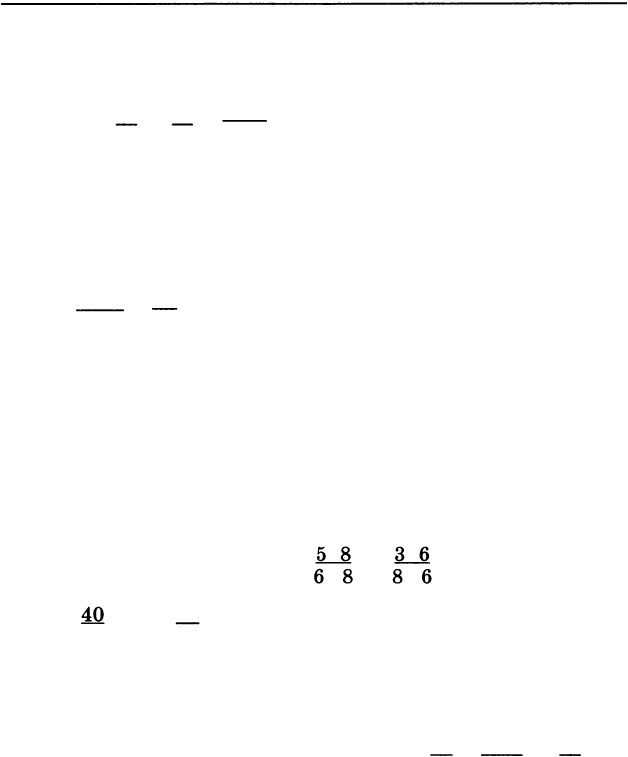
2) Сложение.
I
О
I
а
4
1
,3
i
а
4
i
1
I
1
1
I
»
И куда же мы попали? В какую-то точку, лежа
щую правее единицы. Из рисунка узнать, что это за
точка, мы не можем. Попробуем заменить данные
дроби равными им дробями, но с одинаковыми знаме
нателями. Для этого надо подобрать такую долю, ко
торая помещается целое число раз и в одной трети, и в
трех четвертях. Такой долей может быть, например,
одна двенадцатая - она помещается три раза в одной
четверти, а значит, девять раз в трех четвертях:
3 _
9
4- 12
·
Она же помещается четыре раза в одной трети:
1_
4
3
-12
·
Теперь сложить дроби можно без всякого рисунка:
3 1 _
9
4 _
9 + 4
_
13
4
+
3-12
+
12 -
12
-
12
·
3) Вычитание.
о
184
а
4
1
Глава в
т
о
р
ая.
Дроби
Мы попали в какую-то точку, лежащую между од
ной третью и двумя четвертями. Но теперь мы уже
знаем, как нам быть:
3
_ 1 - 9
_ 4
_
9
-
4
_ .
-12 12
-
1
2
-
12·
Замена дроби на равную ей дробь с другим знаме
нателем называется приведением дро
би к новому
зна
менателю. Эта замена осуществляется с помощью ос
новного свойства дроби. Например, можно привести
дробь � к знаменателю 30:
2 2
· 10 _ 20
=
3·10 -
30
·
Складывая и вычитая дроби : и � , мы приводил
и
их к о
б
щему знаменателю - к знаменателю 12.
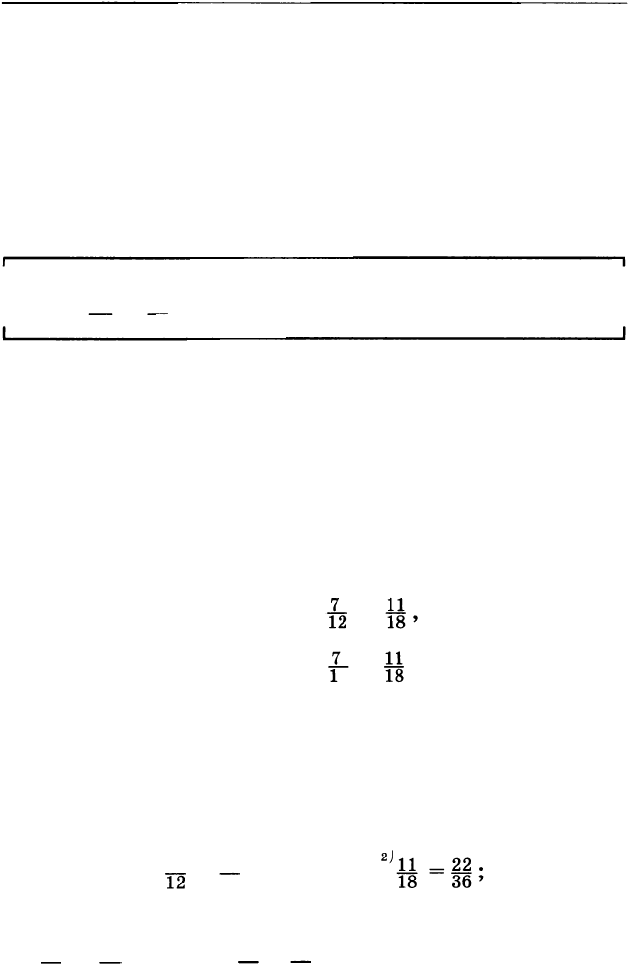
К общему знаменателю можно привести любые две
дроби. Покажем как найти общий знаменатель, на
примере дробей � и �. Воспользуемся основным свой
ством дроби и умножим числитель и знаменатель пер
вой дроби на знаменатель второй (на 8), а числитель и
знаменатель второй дроби на знаменатель первой (на
6). у нас получатся дроби
:
.
.
�
и
:
.
.
�
с равными зна
менателями 6·8 и 8·6. Итак,
Q
_
40
Q _
1
8
6 -
4
8' 8 -
4
8·
А нельзя ли привести дроби � и � к знаменателю,
меньшему, чем 48? Оказывается, можно. Если умно
жить числитель и знаменатель первой дроби на 4,
u
3
5 •
4
2
0 3 • 3 9
а второи - на ,то получим:
н
=
2
4
; 8.
3
=
2
4
·
Нельзя ли сделать общий знаменатель этих дробей
еще меньше, чем 24? Оказывается, нельзя. Ведь но
вый знаменатель получается умножением чисел 6 и 8
на какие-то другие числа, а значит, он должен делить
ся и на 6, и на 8. Но ни одно число, меньшее, чем 24,
не делится на 6 и на 8 одновременно.
Наименьший общий знаменатель данных дробей
можно найти, разложив их знаменатели на простые
185
Глава в
т
ор ая.
Д
ро
би
множители. Для дробей ! и i получится: 6 = 2·3,
8 = 2·2·2. Значит, наименьший общий знаменатель
равен 2
•
3
•
2
•
2. Почему? А потому, что он должен де
литься на 6 и на 8. Значит, он должен содержать по
крайней мере одну тройку и по крайней мере три двой
ки. А раз он наименьший, то никаких других множи
телей он содержать не должен. Значит, наименьший
общий знаменатель данных дробей равен 24.
Задача. Найди наименьший общий знаменатель
б
u 1
1
дро еи
120
и
96
.
I
Впрочем, в тех несложных примерах, с которыми
сталкиваются школьники, обычно удается находить
наименьший общий знаменатель подбором. Кстати,
если даже найти не самый маленький общий знамена
Teль для двух данных дробей, ничего страшного не
произойдет .
Умея приводить дроби к общему знаменателю, мож
но сравнивать, складывать и вычитать любые дроби.
П
ример. Сравним дроби
[
2
и
Ы,
найдем их сумму
и разность.
1) Знаменатели у дробей
l
и
разные. Приведем
их к общему знаменателю 3�. Для этого числитель и
знаменатель первой дроби умножим на дополнитель
ный множитель 3, а числитель и знаменатель второй
дроби - на дополнительный множитель 2. Чтобы не
ошибиться, дополнительные множители подписыва
ют рядом с числителями дробей:
3
) 7 _ 21
•
12
-36 '
2) Выполним действия:
7
11 21
22 .
12
<
1
8
'
так как
36
<
36 '
186
Г
лава в
т
о
р
ая.
Д
ро
би
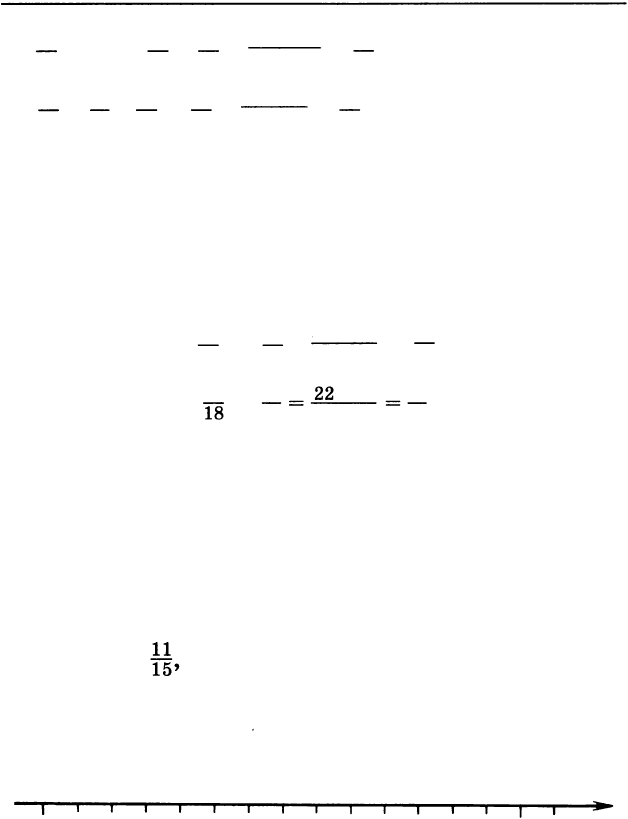
7
+ =
2
1
+
22
=
21
+
22
= 4
2
•
1
2
1
8
36 36
36
36 '
1
1 7 _
22 2
1
_
22 - 21 _
1
1
8
-
1
2
-
36
-
36
-
36
-
36
.
Итак, чтобы сравнить две дроби с разными знамена-
телями и чтобы найти их сумму или разность, нужно:
1) привести дроби к общему знаменателю,
2) выполнить требуемое действие.
В
краткой записи сложение и вычитание дробей
выглядят так:
3
)
7
+
2
)
11
_
2
1
+ 22
_ 43
.
1
2
1
8
-
36
-
36'
2
)11
3
)7
22
-
2
1 1
1
8
-
1
2
36 36·
Мы умели сравнивать, складывать и вычитать на
туральные числа. Теперь мы научились делать то же
самое с любыми дробями. Ну а если взять одно число
натуральное, а другое - дробь? Сможем ли мы их
сравнить между собой, найти их сумму и разность?
На
чнем со сравнения
. Если у дроби числитель
меньше знаменателя, то она меньше любого натураль
ного числа, даже меньше единицы. В самом деле, если
в
з
ять дробь
��,
то ее изображение на координатной
прямой окажется левее единицы, так как единицу на
до ра
з
делить на 15 одинаковых долей и отложить от
нуля вправо 11 таких долей. Но 11 < 15, и полученная
точка окажется левее единицы.
о
15
1
Дроби, у которых числитель меньше знаменателя,
называются правильными дробями. Правильная
дробь меньше единицы и меньше любого натурально
го числа.
187
Глава в
т
о
р
ая.
Д
роби
Дроби, у которых числитель не меньше знаменате
ля (либо равен знаменателю, как у дроби � , либо боль
ше него, как у дроби � ), называются неnрави
л
ьными.
Если числитель равен знаменателю, как у дроби �,
то дробь просто равна единице:
=n:n
=
1
n
Если же числитель больше знаменателя, то что
бы сравнить дробь с натуральными числами, нужно
выде
л
ить ее целую часть. Вот, например,
дробь
2; .
Разделим ее числитель на ее знаменатель. Получим:
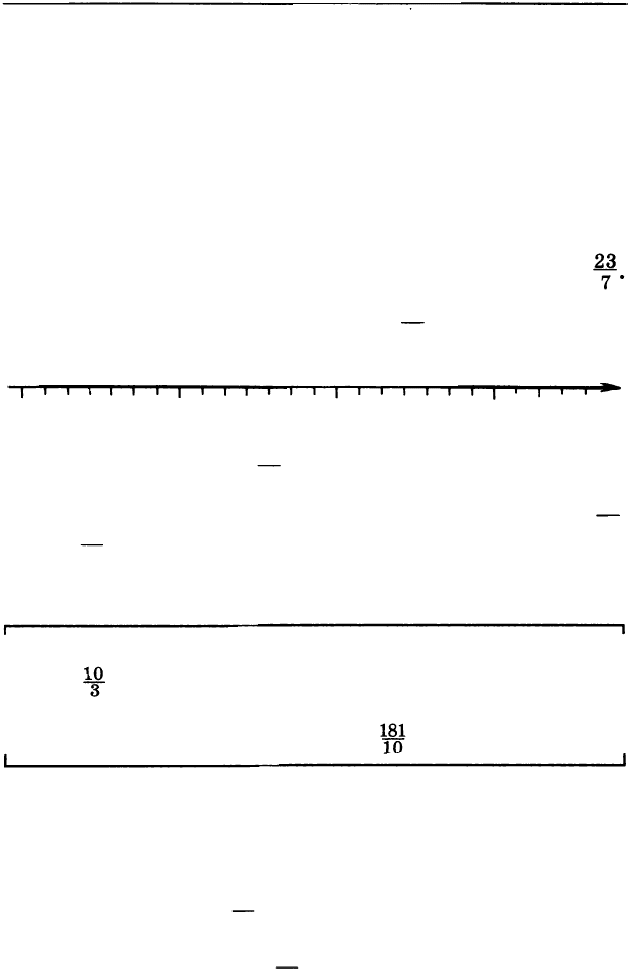
23 : 7 = 3 (ост. 2). Значит, в дроби
2
7
3
содержатся 3 це
лые единицы и еще � . Это хорошо видно на рисунке:
i I i i i I
о
1
i i f I i I
I I i i i i
I
2
2
3
=
3 +
7
7·
3
i
I
i
7
,.
Число 3 - это целая часть неправильной дроби 273.
Число
2
7
3
больше любого натурального числа от 1 до 3;
это число меньше любого натурального числа, начи
ная с 4.
Задача. Выдели целую часть у неправильной
дроби
1�
.
Еще задача. Выясни, между какими натураль
ными числами находится число
\
8
J
.
I
Сумму правильной дроби и натурального числа
обычно записывают в виде так называемого смешан
ного числа: 3 + ,
=
�. Число 3 - целая часть смешан
ного числа �, а , - его дробная часть. Выделив
целую часть дроби
2
7
3
'
мы можем обратить ее в сме-
шанное число:
23
=
з
7
7
·
188
Г
лава
вт
о
р
ая. Д
роб
и
и наоборот, смешанное число можно превратить в
неправильную дробь.
Нап
ри
мер, 1
5
�
=
15 +
�
=
7
;
+
�
=
7
:
.
Подведем итоги. Чтобы сравнить дробь с натураль
ным числом, надо сначала посмотреть, правильная
это дробь или неправильная. Если правильная - она
меньше любого натурального числа. Если неправиль
ная - она либо равна единице, либо больше единицы.
В последнем случае мы выделяем ее целую часть и на
ходим
, между какими соседними натуральными чис
лами заключена дробь.
I
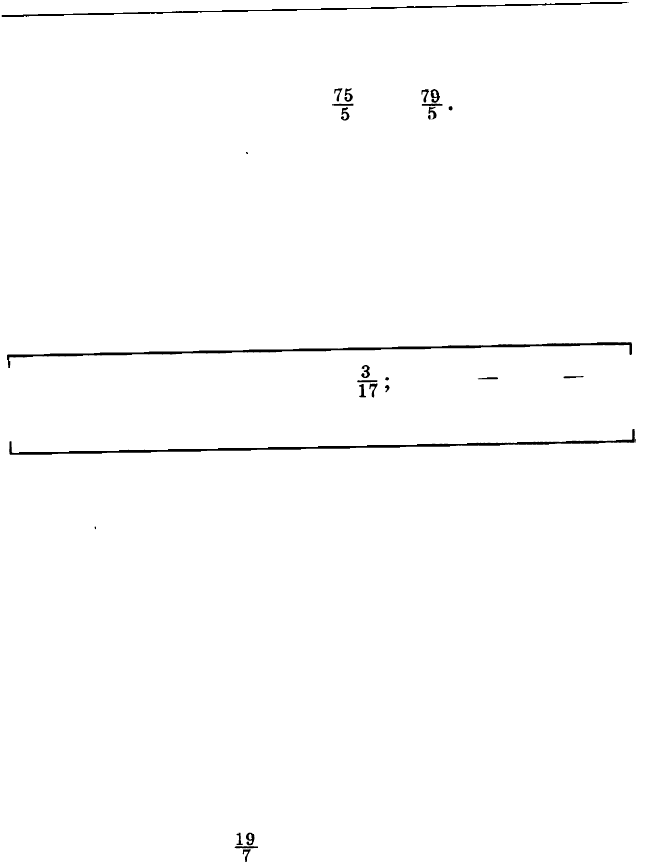
Задача. Сравни числа: 7 и
�
7
;
1
1
5
и 2.
I
и
·
13
и 2
·
,
1
7
2
и 3
·
,
4
'
13
Сложение натурального числа и дроби выполнить
нетрудно. Если дробь правильная - получается сме-
шанное число:
�
+ 5 = 5
�
.
Если дробь неправильная и числитель равен знаме
нателю, то сумма будет на единицу больше данного
натурального числа:
�+ 8 = 9.
Если же дробь неправильная и числитель больше
знаменателя - нужно превратить дробь в смешанное
число и к ее целой части прибавить данное натураль
ное число:
11
+ 6
=
2
�
+ 6 = 8
�
.
Вычитание натурального числа из дроби и вычита
ние дроби из натурального числа - самая неприятная
из всех операций с дробями. Покажем на примерах,
как это делается.
189

Глава вто
р
ая.
Д
ро
би
1. Дробь правильная .
7 -
!
= (6
+ 1) - ! = 6 + (l -
!)
= 6 +
i
= 6
i
.
Вычесть
из
правильной дроби нель
з
я никакое на
туральное число.
2. Дробь неправильная, числитель равен
знамена-
телю.
Это проще всего:
7 -
i
= 7 -1 = 6.
i
- 1 = 1 - 1 = О. Никакое другое натуральное чис
ло
вычесть из
такой дроби нель
з
я.
3. Дробь неправильная, числитель больше
знаме
нателя.
7 -
1
;
= 7 - 2 i = 5 - i - а дальше, как в первом
случае.
1
:
- 2 = 5 ! - 2
= 3 !.
У
м
н
о
ж
е
н
и
е
и деле
н
ие д
р
обе
й
Легче всего умножить дробь на натуральное число
-
для этого достаточно уметь складывать:
х·3
= х + х + х,
и вообще, умножить число на натуральное число n -
значит вз
ять его слагаемым n ра
з
.
Задача. Как узнать, чему равно 4·3, заменяя
умножение сложением?
I
Так и поступим, чтобы умножить число
;
7
на 5:
�.
5=
�
+
�
+
�
+
�
+
�
=
2+2+2+2+2 2·5 10
17 17 17 17 1
7
1
7
1
7
17 17'
190
