Арутюнян Е., Левитас Г. Занимательная математика. 1-5 классы

Подождите немного. Документ загружается.

Глава в

ая.

роби

положив гирю на правую чашку, а второй кило

грамм - положив гирю на левую чашку. Правда ли,

что всего он отвесил ровно 2 килограмма? Если нет, то

как надо было взвешивать?

39. Задача л. Н. Толстого. Косцы нанялись выко

сить 2 луга. Половину дня они косили большой луг, а

потом разделились: одна половина косцов докосила

к вечеру большой луг, а вторая половина косцов пол

дня косила второй луг, который в два раза меньше

первого. Оставшуюся работу доделал за весь следую

щий день один косец. Сколько было косцов?

40. Есть ли такая дробь, которая находится между

дробями

41. Новогодняя елка украшена лампочками. Каж

дая третья лампочка - красного цвета, каждая чет

вертая - синяя, каждая шестая - желтая, а осталь

ные - зеленые. Сколько всего лампочек на елке, если

зеленых на 5 больше, чем желтых?

42. Вода, обращаясь в лед, увеличивается на

часть своего объема. Сколько кубических дециметров

воды образуется при таянии 132 дм3 льда?

лава третья

асширекие разря

ко

сетки

Дес

ти

на

я др

ействия с натуральными числами

выполняются по разрядам. Любое

натуральное число мы можем раз

ложить по разрядам и записать

в разрядную сетку. Но в жизни

нам встречаются не только числа,

состоящие из целого числа единиц,

но и числа, состоящие из долей

единицы. Чаще всего это десятые, сотые, тысячные

доли. Это особенно заметно при всяких измерениях:

дециметр - десятая доля метра; сантиметр - сотая

доля метра; грамм - тысячная доля килограмма.

А нельзя ли такие числа тоже записывать в разряд

ную сетку? Ведь они очень похожи на натуральные

числа: так же, как три единицы в 10 раз меньше, чем

три десятка, так и три десятых в 10 раз меньше, чем

три единицы; а три сотых еще в 10 раз меньше. Похо

же, что для того, чтобы записывать десятые, сотые,

тысячные доли, нам придется продолжить разрядную

сетку вправо.

Попробуем сделать это так, чтобы сохранился ос

новной принцип десятичной системы счисления: зна

чение цифры в каждом разряде в 10 раз меньше, чем

значение той же цифры в соседнем разряде слева. Тог

да правее разряда единиц будет разряд десятых долей

единицы, или просто разряд десятых. Например, циф

ра 2 в разряде десятых обозначает число, которое

в 10 раз меньше, чем 2 единицы. В разрядной сетке

это число записывается так:

202

третья. Р

асширекие ра

ядк

се

аз

ря

тысячи

сотни

ДЕСЯТКИ ЕДИНИЦЫ

десятые

О О

2 десятых

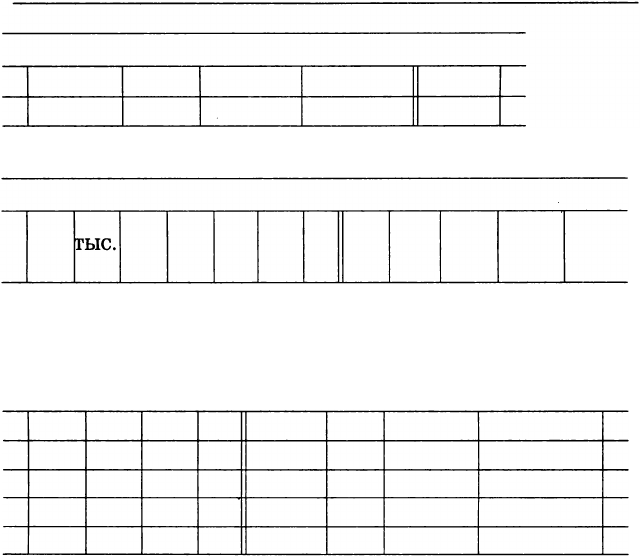
Расширенная разрядная сетка выглядит так:

аз

ря

млн

сот.

ДЕС.

ТЫС.

сот.

ДЕС.

ЕД.

деся·

сотые тысяч·

десяти·

стоты·

ыс.

ТЫС.

тые

ные

тысяч·

сячные

ные

Если число не содержит какого-либо разряда, то

в этом разряде пишут нуль. Например, число, состоя

щее из двух сотен, трех еДиниц и восьми тысячных,

можно записать в разрядной сетке по-разному:

ТЫС.

сот.

ДЕС.

ЕД.

десятые

сотые

тысячные

десятитысяч.

О О

Число, записанное в десятичной системе счисле

ния и имеющее цифры правее разряда единиц, назы

вается

десятичной

дроб

ью. В записи десятичной дро

би после разряда единиц ставится запятая. Запятая

делит

десятичную дробь на целую и дробную части.

Например, у десятичной дроби 23,01 целая часть -

число 23, а дробная часть - 1 сотая. У десятичной дро

би 8,0 дробная часть равна нулю. А у десятичной дроби

0,75 нулю равна целая часть.

ра

нение

ес

тич

др

Мы расширили наш запас чисел - добавили к нату

ральным числам десятичные дроби. Теперь надо на

учиться выполнять над ними привычные действия.

203

Глава

ре

ья

шире

ие ра

рядн

ет

ки

Самое простое - сравнение десятичных дробей.

В этом помогает числовая прямая. Вспомним, как

изображают числа на прямой.

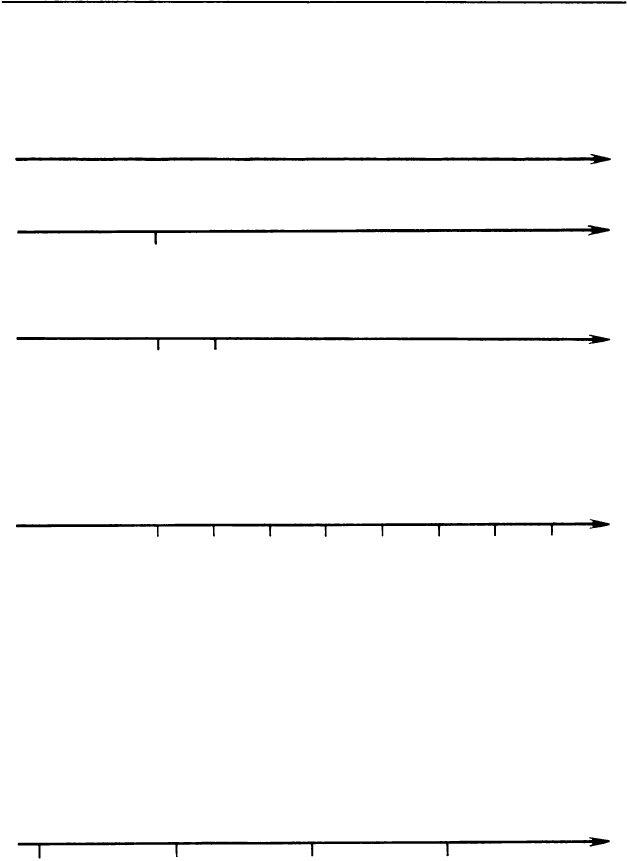
Чертят горизонтьную прямую со стрелкой справа:

Отмечают на ней точку - изображение числа О:

Правее точки О отмечают точку 1:

Отрезок от О до 1 называют единичным отрезком.

Теперь от точки 1 откладываем вправо единичный от

резок - получаем точку 2; затем от точки 2 откладыва

ем вправо еще один - получаем точку 3; и так далее:

у нас получилась числовая (или координатная)

прямая. Из двух чисел больше то, которое лежит пр а

вее на числовой прямой.

А как изобразить на координатной прямой деся-

'тичную дробь? Точно так же. Только вместо целых

единичных отрезков нам придется откладывать их де

сятые, сотые, тысячные доли. Возьмем, например,

число 3,62. Целая часть его равна 3. Изображать чис

ло 3 мы умеем:

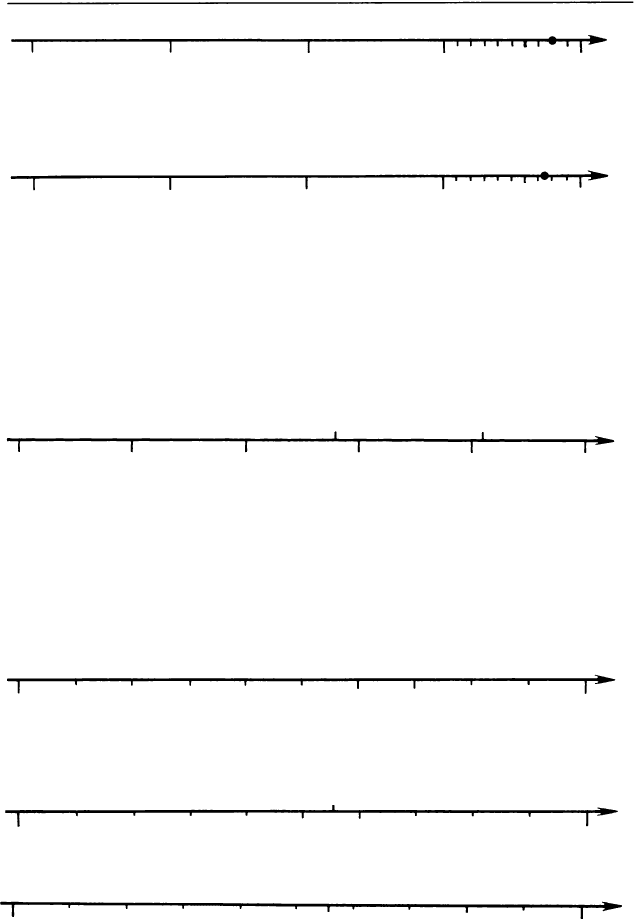
еперь разделим единичный отрезок на десять рав

ных частей и отсчитаем от числа 3 вправо 6 деся

тых - получим число 3,6:

204

Глава

ре

ья.

шире

е ра

яд

НQ

етк

3,6

Наконец, отсчитаем от числа 3,6 вправо две со

тые - получится изображение числа 3,62:

l' , , , ,

,8, ,

3,6

Умея изображать десятичные дроби на числовой

прямой, займемся теперь их сравнением.

Проще всего сравнивать такие десятичные дроби, у

которых неодинаковые целые части. Например, 4,1

лежит правее числа 4, а 2,8 - левее числа 3. Поэтому

4,1 лежит правее числа 2,8:

А значит, 4,1 > 2,8.

2,8

4,1

, -

Теперь попробуем сравнить десятичные дроби с

одинаковой целой частью: 23,8 и 23,56. Оба эти числа

лежат правее числа 23, но левее числа 24. Число 23,8

получается, если отсчитать от числа 23 вправо 8 деся

тых, поэтому оно лежит правее числа 23,7:

23,

23,8

А число 23,56 лежит левее, чем число 23,6:

23,56

23,5 23,6

1 

Значит, число 23,56 лежит левее, чем число 23,8:

23,56

Отсюда видно, что 23,56 < 23,8.

205

23,8

, -

Глава т

ет

я.

асширекие ра

ядк

сетки

Теперь можно с

ормулировать правило сравнения

десятичных дробей.

Из двух десятичных дробей больше та, у которой

больше целая часть. Десятичные дроби с одинаковы

ми целыми частями сравнивают по разрядам их дроб

ных частей: десятые с десятыми, сотые с сотыми и так

далее - до обнаружения неравных знаков в одном и

том же разряде.

Например,

3,94 < 12,05, так как 3 < 12;

16,5891 > 16,58632, так как 16 = 16, 5 = 5, 8 = 8, 9> 6;

17,23 < 17,2315, так как 17 = 17, 2 = 2, 3 = 3

О < 1.

По этому же правилу можно сравнить десятичную

дробь с натуральным числом. Ведь у натурального

числа нет разрядов правее разряда единиц, поэтому

его можно записать в виде десятичной дроби с нуле

вой дробной частью. Например,

13 < 17,11, так как 13 < 17;

13 > 7,185, так как 13 > 7;

13 = 13,00; 13,00 < 13,05, так как 13 = 13, О = О, О < 5.

ение и

вы

ит

ание

Сложение и вычитание десятичных дробей очень по

хоже на сложение и вычитание натуральных чисел.

Найти сумму двух натуральных чисел - значит, уз

нать, сколько в этой сумме единиц, десятков, сотен и

так далее. А чтобы найти сумму двух десятичных дро

бей, нужно, кроме того, узнать, сколько в этой сумме

десятых, сотых, тысячных и так далее.

Вычислим, например, сумму чисел 29,63 и 8,754.

Для этого расположим их в разрядной сетке:

206

Глава

ре

ширекие ра

ядко

тки

...

ЦЫ

десятые

сотые

тысячные

...

7 5

в разрядах, стоящих прав ее тысячных, оба слагае

мых содержат нули. Значит, и их сумма содержит ну

ли в этих разрядах. В разряде тысячных в первом сла

гаемом стоит нуль, а во втором слагаемом - ци

ра 4.

Это значит, что в первом слагаемом О тысячных, а во

втором 4 тысячные. Значит, в сумме будет О + 4 = 4

тысячных. Сотых в сумме будет 3 + 5

8. Десятых бу

дет 6 + 7 = 13. Но 13 десятых - это (3 + 10) десятых,

или 3 десятых + 1 целая. Переносим 1 целую в разряд

целых единиц. Продолжая сложение, получим в це

лой части число 38.

Итак, десятичные дроби складываются по разря

дам, так же, как и натуральные числа. Поэтому их

тоже удобно складывать столбиком. Слагаемые запи

сывают так, чтобы ци

ры одного и того же разряда

оказались друг под другом. При этом оказываются

друг под другом и запятые:

+ 29,630

8,754

38,384

По разрядам выполняется и вычитание десятич

ных дробей; при вычитании столбиком числа подпи

сывают так же, как при сложении: разряд под разря

дом, запятая под запятой:

43,687

6,945

36,742

207

Глава

тр

ья. Расш

ирение ра

ряд

но

сетки

Точно так же поступают и в том случае, когда одно

из слагаемых, вычитаемое или уменьшаемое, - на

туральное число:

+ 17,305

21,305

12,713

9,713

19,208

3,792

ие и деле

ие

10, 100, 1000

Проще всего умножать и делить десятичные дроби

на 10, 100, 1000 и вообще на любое число, которое за

писывается единицей с несколькими нулями.

Умножим, например, число 4,85 на 10. Для этого

используем распределительное свойство умножения:

4,85 ·10 = (4 единицы + 8 десятых + 5 сотых) ·10 =

= 40 единиц + 80 десятых + 50 сотых =

= 4 десятка + 8 единиц + 5 десятых = 48,5.

Получилось, что 4,85 · 10 = 48,5.

Мы видим, что при умножении числа на 1 О каждая

цифра этого числа переходит в соседний разряд влево.

Это значит, что при умножении десятичной дроби на

10 запятая перемещается на один знак вправо:

�

85 · 10

�

А может запятая при этом и совсем пропасть:

22,7· 10 = 227 .

Умножить число на 100 можно так: сначала умно

жить его на 10, а потом результат умножить еще на

10. Поэтому при умножении десятичной дроби на 100

запятая перемещается на два знака вправо:

�

14159 · 100

314

�

159;

172

�

07 · 100 = 17207 .

208

Глава

тр

ья. Расширекие ра

ядк

й сет

Точно так же умножение на 1000 можно провести

как троекратное умножение на 10. Значит, запятая

переместится на

знака вправо:

8.1305 · 1000 = 8130.5;

42.15 · 1000 = 42150 .

Ясно, что при делении на такие числа запятая пу

тешествует в обратном направлении:

4,85 · 10 = 48,5;

22,7·10 = 227;

3,14159 · 100 = 314,159;

172,07 ·100 = 17207;

8,1305 · 1000 = 8130,5;

42,15· 1000 = 42150;

Запомни такое правило:

48.5 : 10 = 4.85.

227 _ : 10 = 22.7.

314.159 : 100 = 3.14159.

17207 _ : 100 = 172.07.

8130.5 : 1000 = 8.1305.

42150

: 1000 = 42.15.

Чтобы умножить десятичную дробь на число, ко

торое записывается единицей с несколькими нуля

ми, достаточно перенести запятую вправо на столь

ко знаков, сколько нулей в этом числе.

Чтобы разделить десятичную дробь на такое чис

ло, достаточно перенести запятую влево на столько

же знаков.

мн

ие л

бы

исел

ти

чно

�

теме

исле

Предположим, надо умножить 13,1 на 3,17. Первый

множитель в 10 раз меньше числа 131. Второй множи

тель в 100 раз меньше числа 31 7. Поэтому произведе

ние 13,1 · 3,17 можно найти так: умножить 131 на 317,

результат разделить на 10, а потом еще на 100. Или ко-

8-22

209

Глава

ре

ья. Р

асшире



ие ра

яд



сетки

роче: умножить 131 на 317 и разделить результат на

1000. А разделить на 1000 - значит, сдвинуть запятую

влево

на 3 знака. Запомни еще одно правило:

Чтобы умножить числа, записанные в десятич

ной системе счисления, нужно найти их произведе

ние, не обращая внимания на запятые, и отделить в

нем запятой справа столько знаков, сколько их сто

ит после запятых во всех множителях вместе.

Например, в произведении 45,6 ·7· 0,0002

= 0,06384 отделено запятой 5 знаков, так как в пер

вом множителе 45,6 имеется один знак после запятой,

во втором множителе 7 таких знаков нет, в третьем

множителе 0,0002 их 4, а значит, всего в этих множи

телях 1 + О + 4 = 5 знаков после запятых.

Разберемся в этом правиле на примере умножения

чисел 1,28 и 0,064.

1) Не обращаем внимания на запятые - заменяем

десятичные дроби натуральными числами:

1,28 � 128;

0,064 � 64.

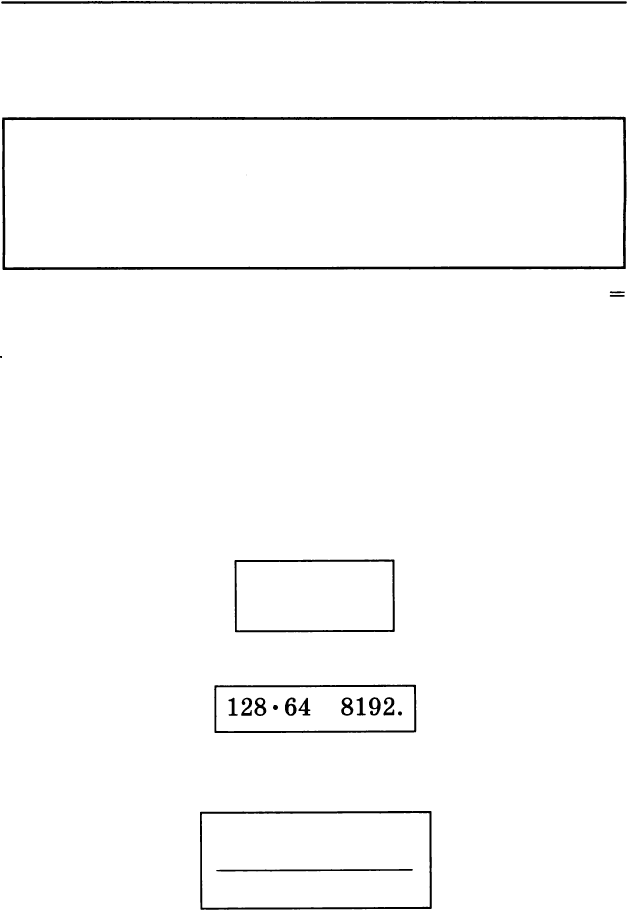
2) Находим произведение полученных чисел:

1128 .64

8192· 1

3) Подсчитываем число знаков после запятых во

всех данных множителях:

1,28

2 знака

0,064 - 3 знака

всего

5 знаков

4) В произведении 8192 отделяем запятой 5 знаков

справа:

210