Арутюнян Е., Левитас Г. Занимательная математика. 1-5 классы
Подождите немного. Документ загружается.


r
ла
в
а третья. Расшире
ие ра
з
р
яд
о
й
сетки
1
8
1
92
�
0,08
1
92· 1
5) и вот (ура!) мы получили ответ:
1
1
,28.0,0
6
4
=
0,08
1
92· 1
Пока человек только учится применять это прави
ло, приходится записывать решение подробно, как
это сделано в рамочках.
А когда правило умножения хорошо запомнится,
полезно еще некоторое время выполнять все пять ша
гoB (заменять десятичные дроби натурьными чис
лами; перемножать эти числа; подсчитывать число
знаков после запятых; отделять запятой знаки в про
изведении; выписывать ответ), но делать при этом
краткие записи. Они могут выглядеть так:
х
1
,2
8
+ 2 знака
0,0
6
4
3
знака
+ 5
1
2
76
8
О, О
8
1
9 2
5 знаков
Ответ: 0,08
1
92.
Из правила умножения, между прочим, следует,
что умножить десятичную дробь на 0,
1
- значит
сдвинуть запятую на
1
знак влево. А это означает про
сто деление на
1
0. Это же'относится и к умножению на
0,0
1
, 0,00
1
и так далее.
Умножение на 0,
1
, на 0,0
1
, на 0,00
1
и так далее
можно заменить делением на
1
0,
1
00,
1
000 и так далее.
Умножение на
0,1
0,01
0,001
. . . .....
0,0000000000001
211
Деление на
10
100
1000
.
. ..... .
10000000000000
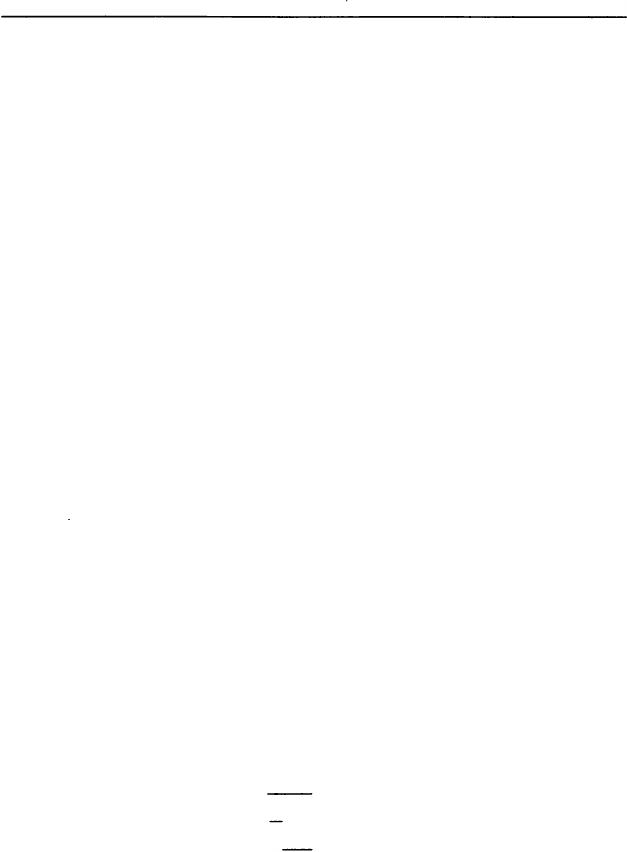
Глава
тр
е
т
ья.
Р
асшире
ие ра
з
р
яд
Q
Й
сетки
Де
л
ение
Самое трудное действие, как известно, деление. Деле
ние десятичных дробей, так же как и деление на
туральных чисел, можно выполнить не всегда. Но все
же с появлением десятичных дробей количество
примеров на деление, которые можно решить, увели
чивается. Например, разделить 70 на 8 в натураль
ных числах нельзя, а с десятичными дробями можно:
70 : 8 = 8,75 - это легко проверить умножением.
Как мы видели, умножение десятичных дробей сво
дится к умножению натуральных чисел и постановке
запятой. Естественно, что и деление десятичных
дробей оказывается связано с делением натуральных
чисел. Если, например, надо разделить какое-нибудь
число на десятичную дробь 28,17, которая в 100 раз
меньше числа 2817, это значит, что достаточно разде
лить его на 2817, а потом частное увеличить в 100 раз.
Поэтому деление любого числа, записанного в десятич
ной системе счисления, на натуральное число заслужи
вает отдельного разговора.
Разделим 376,96 на 31. Чтобы найти частное от деле
ния двух чисел, достаточно найти его целую часть и най
ти, сколько в нем десятых, сотых, тысячных и так далее.
1) Найдем целую часть частного. Она получится, ес
ли
разделить на 31 целую часть делимого
- число 376:
_
376
31
12
66
62
4
Получилось, что в частном 12 целых.
2) Чтобы найти дробную часть частного, превратим
остаток от деления целой части - 4 единицы - в со
тые и найдем, сколько сотых надо делить на 31:
212
Глава т
р
етья. Расширек
и
е ра
з
рядко
й
сетки
4 единицы + 96 сотых = 400 сотых + 96 сотых
= 496 сотых.
Разделив 496 сотых на 31, найдем дробную часть
частного:
_
496
31
16
186
-186
О
3начит, 496 сотых : 31 = 16 сотых.
Итак, в частном 376,96 : 31 содержится 12 целых и
16 сотых:
376,96 : 31 = 12,16.
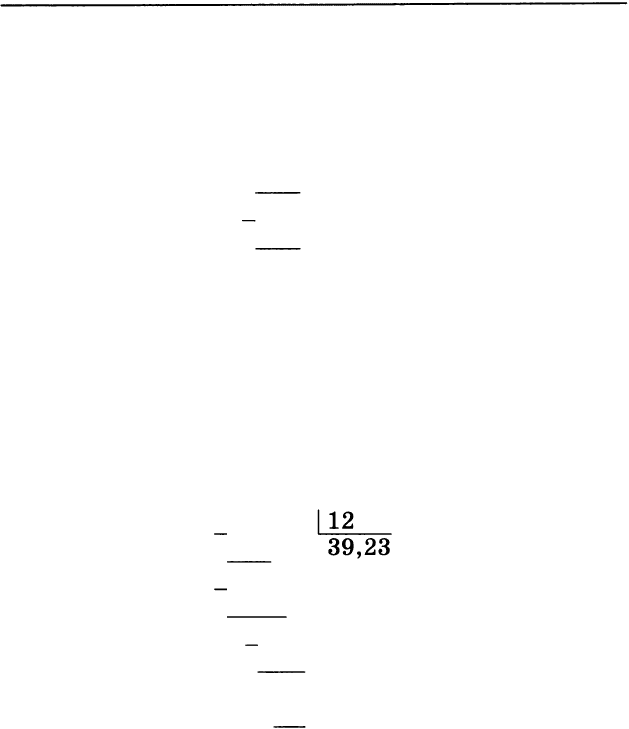
Д
еление на целое число можно провести и сразу,
с начала до конца. Нужно делить, как делят нату
ральные числа, и только вовремя поставить запятую:
470, 76
1
1
2
36
39,23
110
108
27
24
36
-
36
О
Момент, когда нужно ставить в частном запятую,
совпадает с моментом снесения первого знака из
дробной части делимого.
Итак, выполняя деление на натуральное число, мы
сначала делим целую часть делимого; когда заканчи
вается деление целой части (сносится ци
ф
ра, стоящая
в разряде десятых), в частном ставится запятая и де
ление продолжается.
213
Глава третья.
Ра
сш
u
ре
u
е ра
з
рядк
ой с
е
m
"
и
На первых порах рекомендуется записывать деле
ние двумя ручками разного цвета, например черной
и зеленой. Черным цветом записывают делимое и де
литель, зеленым обводят ци
ф
ру десятых в делимом:
376,9
6 �
Затем выполняют деление черной ручкой, пока не
закончится целая часть делимого, то есть пока не
придется сносить обведенную ци
ф
ру десятых:
_
376,96 �
31
12
66
62
4
Обведенную ци
ф
ру десятых сносят зеленым цве
том и тем же цветом ставят запятую в частном:
_
376,96
�
12,
66
62
49
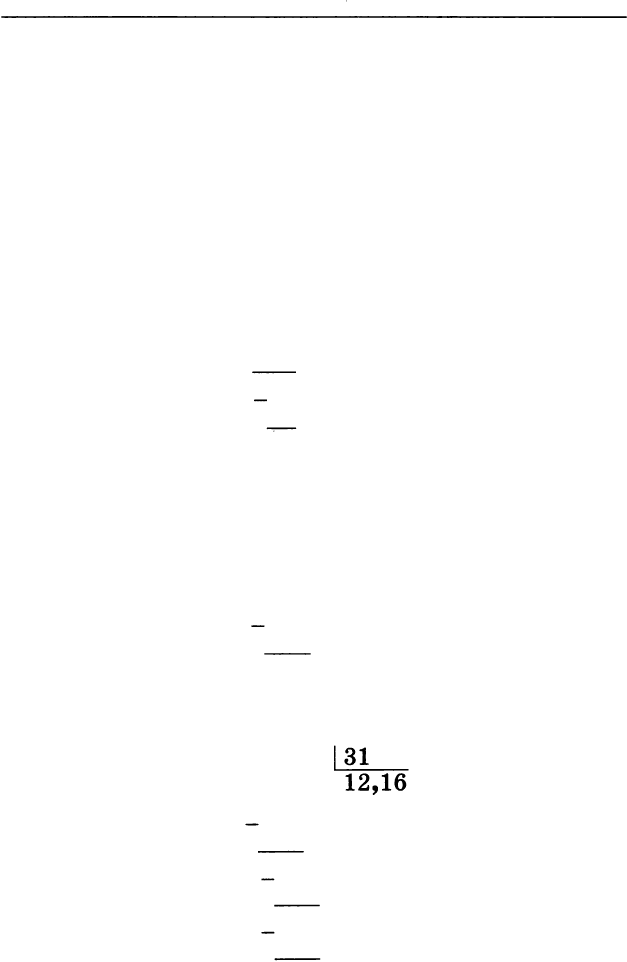
Деление продолжают до конца черной ручкой:
_
376,96
1
3
1
�
12,16
66
62
49
31
186
186
О
214

Глава
тр
е
т
ья. Р
асширекие ра
з
р
ядк
о
й
сет"
и
Наконец мы подошли к вопросу: как же найти ча
стное, если делитель - десятичная дробь? Для этого
воспользуемся важным свойством частного: оно не
меняется, если и делимое, и делитель умножить на
одно и то же число, не равное нулю.
Разделим, например, 1,04 на 1,3. Это действие лег
ко заменить делением на натуральное число 13 -ведь
частное не изменится, если и делимое 1,04, и дели
тель 1,3 умножить на 10:
1,04 : 1,3 =
( 1,04 ·10) : (1,3 · 10) = 10,4 : 13.
Осталось разделить 10,4 на натуральное число 13,
а это мы умеем:
10,4 �
о
0,8
104
104
О
Итак, 1,04 : 1,3 = 0,8.
Так деление на десятичную дробь заменяют деле
нием на натуральное число: делимое и делитель
увеличивают в одно и то же число раз
(
10, 100, 1000 и
так далее) таким образом, чтобы превратит
ь
делитель
в натуральное число.
Итак, чтобы выполни�ь деление на десятичную
дробь, нужно:
1) заменить делитель натуральным числом и уста-
новить, во сколько раз он от этого увеличился;
2) увеличить во столько же раз делимое;
3
) выполнить деление полученных чисел.
Вот подробная запись деления числа 31,26 на деся
тичную дробь О, 015:
1) 0,015 15;
15 = 0,015· 1000.
2) 31,26 · 1000 = 31260.
215
Глава третья
. Р
асш
u
рек
u
е ра
з
рядк
о
й
сет
х
и
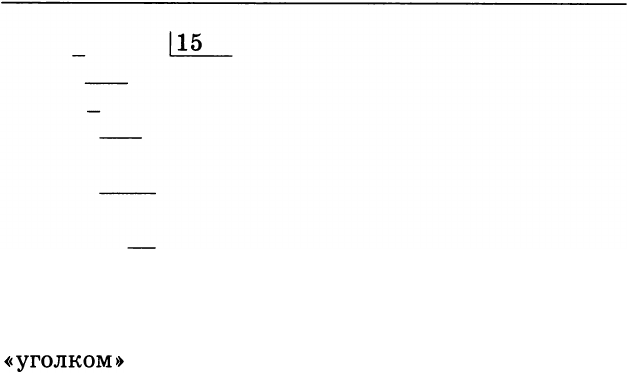
3
)
31260
115
30
2
084
12
О
126
-
120
60
-
60
О
Этот же пример кратко записывается так:
31,26 : 0,015 = 31260 : 15, и дальше - деление
« уголком»
.
Разделим по этому правилу 3,14 на 0,1:
3,14 : 0,1 = 31,4 : 1 = 31,4.
Как видно, деление на 0,1 - это то же самое, что
умножение на 1 о.
Точно так же 27,5 : 0,001 = 27500 : 1 = 27500; деле
ние на 0,001 -то же самое, что умножение на 1000.
Итак, чтобы разделить число на 0,1, на 0,01, на
0,001 и так далее, надо его умножить на 10, на 100, на
1000 и так далее.
П
роц
ен
т
Процентом от какого-нибудь числа называется одна
сотая часть этого числа. Процент обозначается специ
альным значком % .
Нужно уметь решать три главные задачи на про
центы.
Задача п
е
р
вая. Найти несколько процентов от дан
ного числа (например, найти 17% от числа 25
)
.
216

r
лава
третья
. Р
асширекие ра
з
рядк
о
й
с
е
т
ки
Подробное решение.
1) Находим 1 % от данного числа, разделив это
число на 100 (в нашем примере пишем: 1% - это
25 : 100 = 0,25)
.
2) Находим нужное число процентов, умножив ре
зультат первого действия на нужное число (в нашем
примере пишем: 17% - это 0,25
•
17 = 4,25
)
.
Краткое решение:
2
���
7
= 4,25.
Можно решать и по-другому, пользуясь тем, что
разделить на 100 - все равно что умножить на 0,0 1.
Поэтому, чтобы найти 1 % от данного числа, можно
это число умножить на 0,01. Тогда краткое решение
нашей задачи запишется в строчку:
25· 0,01
•
17 = 4,25.
Задача
втор
а
я
.
Найти число, зная, чему равен ка
кой-либо процент от него (например, найти число,
13% которого равны 65
)
.
Подробное решение.
1
) Находим 1 % от искомого числа, разделив дан
ное нам число на число содержащихся в нем процен
тов (в нашем примере пишем: 1 % - это 65 : 13 = 5).
2) Находим все число, умножив результат первого
действия на 100 (в нашем случае пишем: 100% - это
5· 100 = 500).
Краткое решение: 65
i�OO
= 500.
За
д
ача
третья
.
Найти процентное отношение двух
чисел, то есть найти, сколько процентов составляет
одно число от другого (например, найти процентное
отношение 36 и 120, то есть найти, сколько процентов
составляет число 36 от числа 120).
217
Гл
ав
а трет
ья. Расшир
еки
е ра
з
р
ядко
й
сет
"
и
Подробное решение.
1) Находим 1 % от второго числа, разделив его на 1 00
(в
нашем примере пишем: 1 % -это 120 : 100 = 1,2).
2) Находим, сколько процентов от второго числа
содержится в первом числе, разделив первое число на
результат первого действия (в нашем примере пишем:
36 : 1,2 = 30).
Краткое решение:
3
6
;o
= 30.
Все три задачи можно решить, пользуясь одной и
той же таблицей:
100%
1%
%
Вот как заполняется эта таблица при решении
каждой из наших задач.
Задача п
е
р
ва
я. Найти
2,8% от
50 кг.
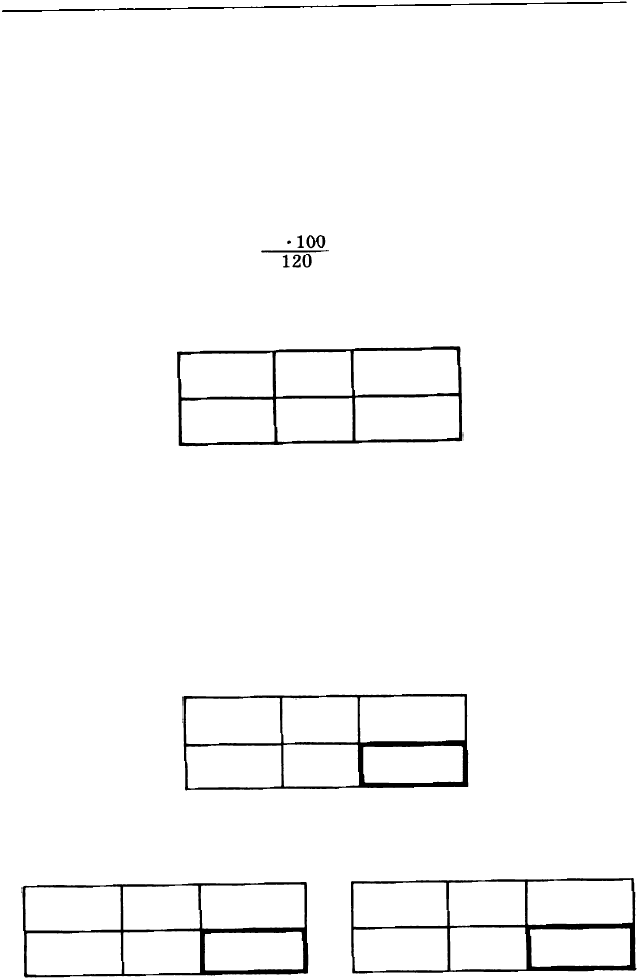
Вначале заполняем по условию третью клетку
верхней строки и первую клетку нижней строки и об
водим ту клетку, в которой должно появиться число,
о котором спрашивается в задаче:
100%
1%
2,8%
50 кг
Затем, после необходимых вычислений, заполня
ем пустые клетки нижней строки:
100%
1%
2,8%
100%
1 %
2,8%
50 кг
0,5 кг
I
50 кг
0,5 кг
1,4 кг
218
r
л
а
в
а третья. Р
асширекие ра
з
рядк
о
й
сетки
Задача
втор
а
я
.
Найти длину пути, 40% которого
равны 16 км.
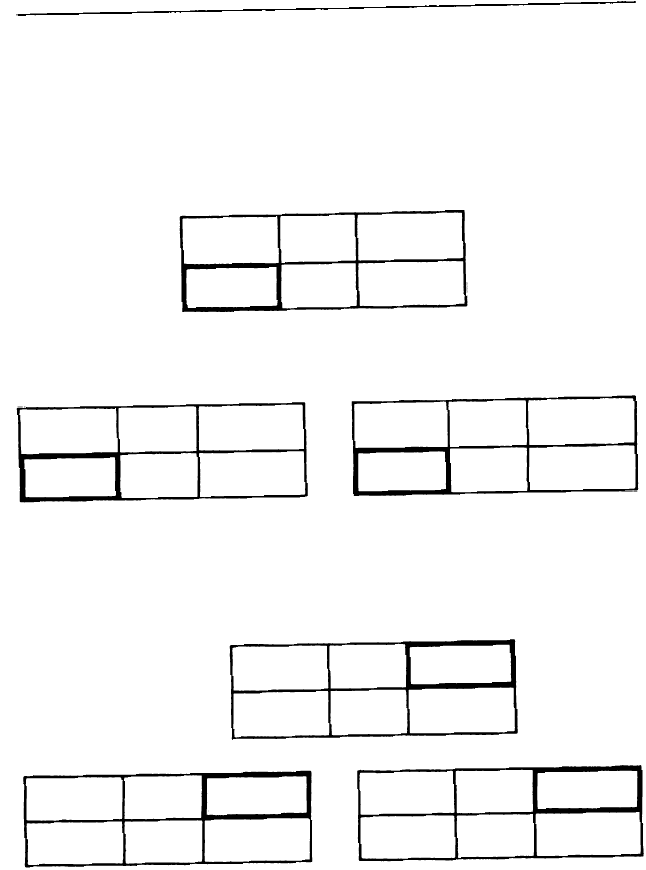
Вначале заполняем по условию третью клетку
верхней строки и третью клетку нижней строки и об
водим ту клетку, в которой должно появиться число,
о котором спрашивается в задаче:
100%
1%
40%
16 км
После вычислений заполняем вторую, а затем пер
вую клетки нижней строки:
100%
1 %
40%
100%
1
%
40%
0,4км
16
к
м
40 км
0,4км
16 км
Задача
третья
.
Найти процентное отношение 48 к 25.
Таблицу заполняем в следующем порядке:
100%
1%
%
25
48
100%
1
%
%
100%
1%
192%
25
0,25
48
25
0,25
48
Но самое интересное в процентах - это то, что они,
собственно говоря, не числа. Вот, например, если ка
кое-то число увеличить на 10, а потом уменьшить на
10, что получится? Конечно, то же самое число. А что
219

Глава третья
. Р
асш
ир
ек
ие ра
з
р
ядк
о
й
сетки
будет, если число увеличить на 10% , а потом умень
шить на 10%?
Вот какая история приключилась однажды с изве
стными всем персонажами Григория Остера: Мар
тышкой, Попугаем, Слоненком и Удавом.
Однажды Удав сказал: «Надоело
мне ползать по
земле. И не видно ничего, и медленно. Давайте купим
заводной вертолет и посадим в него меня ».
-
« И ме
ня, - закричала Мартышка. - Мы полетим быстрее
Попугая!»
- «Это
мы еще
посмотрим»,
- возразил
Попугай. А Слоненок очень огорчился:
«Меня в завод
ной вертолет не посадишь - авария будет! И крыльев
у меня
нет» .
Удав утешил его:
«Ты
будешь судьей на
шего соревнования. Вот только где взять вертолет?
»
-
«Я
придумала! - завопила Мартышка. - Пусть По
пугай слетает в игрушечный магазин. Вертолет стоит
сто бананов, и я их сейчас
соберу» .
Собрала Мартышка сто бананов, положила их
в большой рюкзак, и Попугай полетел в город. Вернул
ся он очень быстро, с пустым рюкзаком. «Где
мой вер
толет?»
- спросил Удав.
«Где
мои
бананы?» ·-
закри
чала Мартышка. «Вертолеты подорожали, - объявил
Попугай, - на 10% . Так что бананов не хватило, и я
раздал их детям. Они сказали мне, что завтра вертоле
ты снова подешевеют. И опять на 10%
».
Наутро Попугай, захватив новые сто бананов, по
летел в магазин. Скоро он вернулся с прекрасным
заводным вертолетом. «Получай!»
- сказал Попу
гай Удаву и облизнулся. «А
почему это ты облизы
ваешься? » - подозрительно спросила Мартышка.
«А
потому, что я съел оставшийся
банан» .
-
«Ничего
не понимаю! - сказал Удав, заползая в вертолет. -
Вертолет сначала стоил сто бананов. Потом он подо
рожал на 10% , а потом подешевел тоже на 10%
».
-
«А
я тебе дала ровно сто
бананов»,
- вмешалась
220
