Арутюнян Е., Левитас Г. Занимательная математика. 1-5 классы

Подождите немного. Документ загружается.

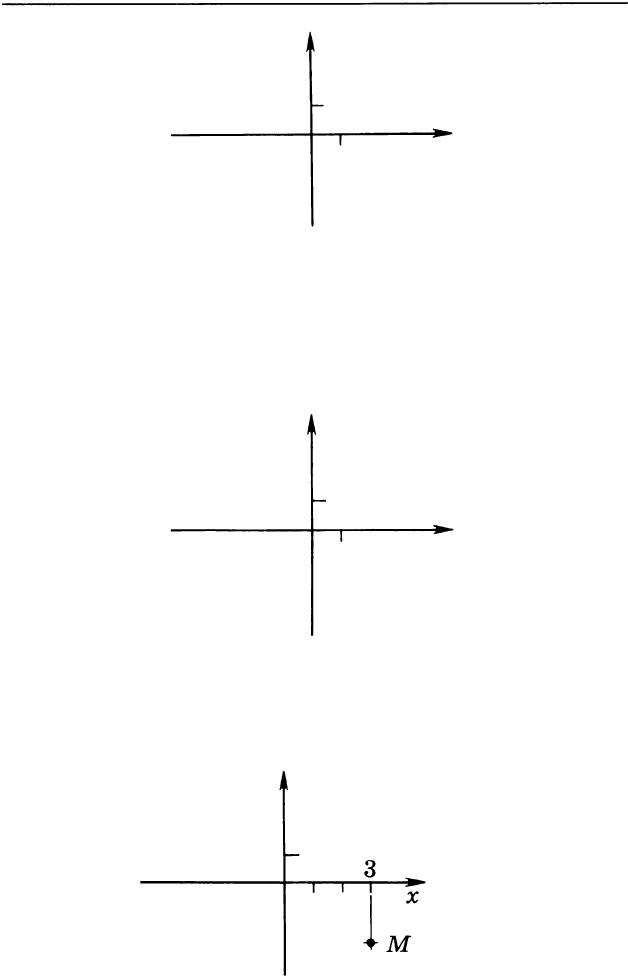
Глава четве

тая.

ациоальые числа

То, что у нас получилось, называется пр

ямоуголь

сис

тем

оо

рд

инат. Прямая

х назыв

ается

ью

бс

исс

, прямая О

ью

орд

нат. Прямоугольная

система координат позволяет любую точку плоскости

обозначить двумя числами - координатами. Возьмем

на плоскости точку

·м

Проведем через точку

вертикальную прямую.

Она

пересечется с осью абсцисс в точке, изображаю

щей

на этой оси какое-нибудь число (у нас получилось

число

3).

Это число называется

бсциссой

точки

М.

абс

исса

точки М

231

ва че

вер

ая.

u



ые ч

Значит, чтобы найти абсциссу точки М, нужно:

1) провести через точку М вертикальную прямую,

2) найти точку пересечения прямой с осью абсцисс,

3) найти координату точки пересечения - это абс

цисса точки М.

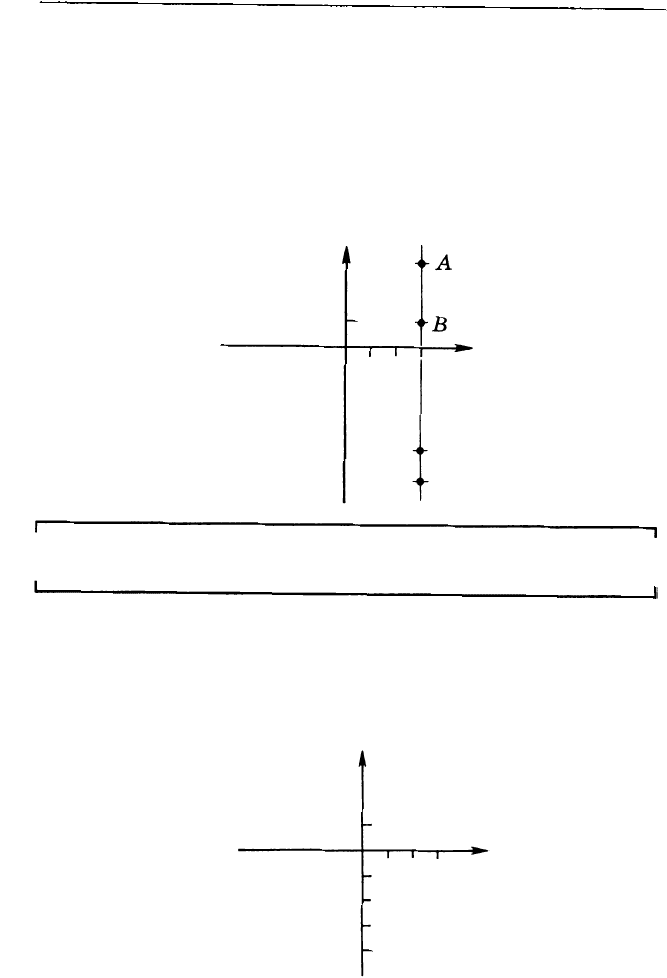
Чтобы найти точку на плоскости, одной абсциссы

мало. Например, точки А,

и С имеют такую же абс

циссу, как и точка М:

3 х

Задача. Изобрази как можно больше точек, имею-

щих абсциссу 3.

Теперь про ведем через точку М еще одну пря

мую - горизонтальную - до пересечения в некото

рой точке с осью ординат. Эта точка обозначает на оси

ординат какое-то число (в нашем случае - число

4).

Это число называется ор динатой точки М.

-4 - ордината

точки М

232

Глава четве

тая.

ациоальые числа

Значит, чтобы найти ординату точки М, нужно:

1) провести через точку М горизонтальную пря

мую,

2) найти точку пересечения этой прямой с осью ор

динат,

найти координату точки пересечения - это ор

дината точки М.

Задача. Изобрази как можно больше точек, имею

щих ординату -4.

Абсцисса и ордината точки называются ее коорди

натами: абсцисса - первая координата, ордината -

вторая координата. Точка А с абсциссой х и ординатой

записывается так: А (х;

). На первом месте всегда

пишут абсциссу, а на втором - ординату.

Например, точка М на нашем рисунке имеет коор

динаты 3 и -4 и записывается так: М (3; -4).

Зная абсциссу и ординату точки, можно построить

эту точку в прямоугольной системе координат. Постро

им, например, точку А (5; -1). Сделаем это в два этапа:

1) найдем на оси абсцисс точку 5 и проведем через

нее вертикальную прямую;

2) найдем на оси ординат точку -1 и проведем через

нее горизонтальную прямую.

1

-1



Проведенные прямые пересекаются в точке А (5; -1).

233

Глава четвертая.

ациоальые чис

иво

жн

ые ч

а.

оду

а.

ые

иона

ые ч

ис

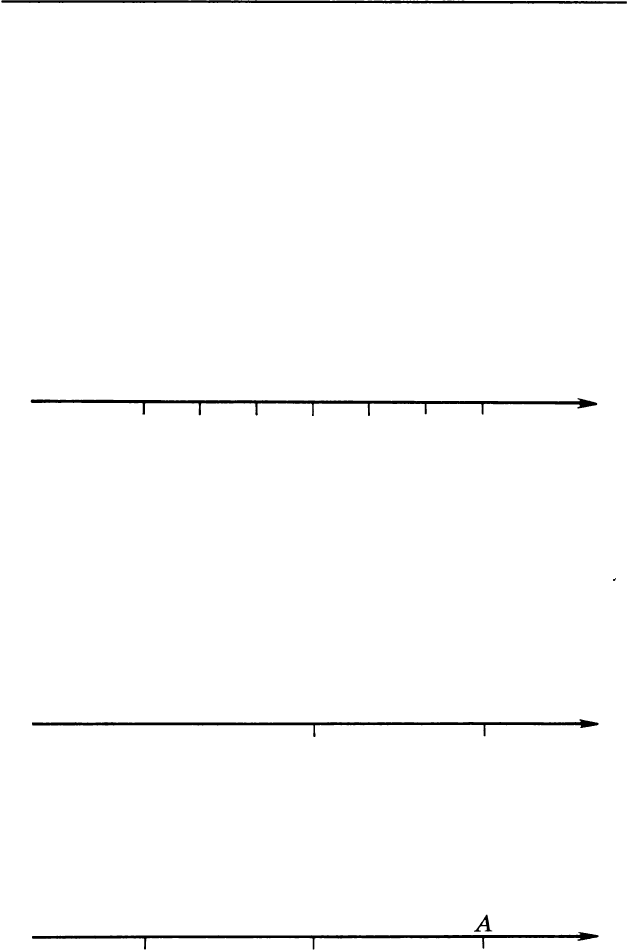
На расстоянии трех единичных отрезков от нуля на

координатной прямой находятся два числа: 3 и

Два числа, расположенные на числовой прямой по

разные стороны от нуля и одинаково удаленные от не

го, называются противоположными числами. Число

О считается противоположным самому себе. Напри

мер, числа 3 и -3 противоположные, так как каждое

из них удено от нуля на 3 единицы и они располо

жены по разные стороны от нуля:

-3

Число, противоположное числу а, обозначается

-а. Например,

3 - это число, противоположное чис

лу 3. А

-(-

3) - это число, противоположное числу -3,

то есть число 3. Так что число -а не обязательно отри

цательное. Если а - положительное, то -а - отрица

тельное; если а - отрицательное, то -а - положи

тельное; если а

о, то -а

о.

Пусть число х изображено точкой А на числовой

прямой:



Тогда противоположное ему число -х можно найти

так: отложить от точки

отрезок, равный отрезку

А, в другую сторону от точки А. Получится точка В,

удаленная от нуля на то же расстояние, что А, но ле

жащая с другой стороны:

234

лава че

вер

ая.

ац

ио

ль

чи

Значит, точка В изображает число -х, противопо

ложное числу х.

-х

Такую точку В можно найти только одну. Так что

у всякого числа есть ровно одно противоположное ему

число. Отсюда вытекает очень интересное правило:

- (-а)

Ведь число - (-а) противоположно числу -а. И чис

ло а тоже противоположно числу -а. А так как у чис

ла -а всего одно противоположное число, то - (-а)

а.

Расстояние от числа на числовой прямой до нуля

имеет специальное название: оно называется модулем

числа. Модуль числа х обозначается двумя верти

кальными черточками: Ixl.

Например, число - 8 находится на расстоянии 8 еди

ниц от нуля, и поэтому его модуль равен 8. Пишем:

= 8. Число О удалено от нуля на О единиц, поэтому

модуль нуля равен нулю:

1 =

о. А число 3,8 удалено

от нуля на

3,8 единицы:

3,8

1 =

3,8.

Определение модуля числа а можно записать в ви

де

ормулы:

{а, если а > О,

О, если а

О,

-а, если а < о.

Например.

= 5, так как 5 > О (первая строка

ормулы),

1 =

о (вторая строка

ормулы),

- (

7 (третья строка

ормулы).

Теперь есть числа и в левой части числовой пря

мой. Натуральным числам 1, 2,

3, 4, ... , лежащим

прав ее нуля, соответствуют противоположные им

235

Глава четвертая.

Ра



иокалькые числа

числа -1, -2, -3, -4, ... , лежащие левее нуля. Их раз

деляет число нуль. Все они: натуральные числа, чис

ло нуль и числа, противоположные натуральным, -

называ

ются целыми числами. Кроме натуральных

чисел, справа от нуля располагаются дроби, а слева от

нуля находятся числа, противоположные дробям.

Целые числа, дроби и числа, противоположные дробям,

называются рациональным

и числами.

Задача. Какие из следующих утверждений верны:

)

всякое натуральное число - целое;

всякое целое число - натуральное;

3) всякое рациональное число - целое;

4) всякое рациональное число - положительное;

)

всякое натуральное число - положительное;

6) нуль - рациональное число;

,7 - целое число;

) 0,7 - рациональное

число;

) -2

9 - целое число?

Определить рациональные числа можно и по-дру

гому: это числа, которые можно записать в виде �, где

т - число целое, а n - число натуральное. Вот при

еры

17 - целое, 1

натуральное;

= �, о - целое, 1

натуральное;

-12

;8,

128 - целое,

1 - натуральное;

2,36

��,

236 - целое, 100 - натуральное;

;

-�3

13 - целое, 7 - натуральное.

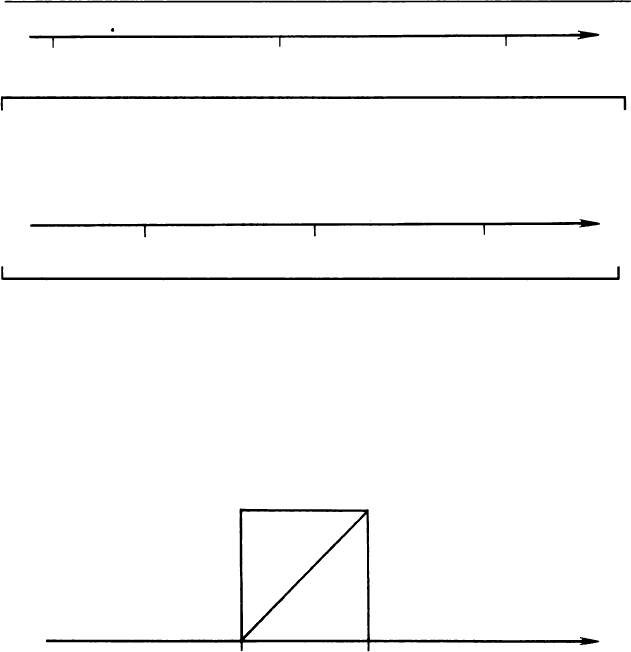
Числовая прямая плотно покрыта рациональными

числами. Между любыми двумя числами, как бы

близко друг к другу они ни стояли, обязательно

найдется еще одно рациональное число. Например,

между числами 2 и 2,

000001 находится число

2,0000005.

236

Глава че

вер

ая.

Ра



иокалькые чи

ла

2,0000005

,000001

Задача. а и Ь - рациональные числа. Какое"из сле

дующих чисел обязательно находится между ними:

а + Ь, а - Ь, аЬ, аЬ : 2, (а + Ь) : 2?

•

Но самое интересное - то, что рациональные чис

ла вовсе не заполняют всю числовую прямую. На пря

мой бесконечно много чисел, не являющихся рацио

нальными (их называют иррациональными). Оказы

вается, если взять квадрат со стороной в 1 см, то

длина его диагонали выражается иррациональным

числом сантиметров. Но это уже относится к высшей

математике.

ло

ие

иональ

ны

исел

ислово

й п

рямо

Наш запас чисел опять увеличился. Значит, опять

надо учиться сравнивать, складывать, вычитать, ум

ножать и делить.

Сравнивать рациональные числа очень легко, изо

бражая их на числовой прямой: чем прав ее число, тем

оно больше, а чем левее, тем меньше.

237

а че

вер

я. Ра

цио

калькые числа

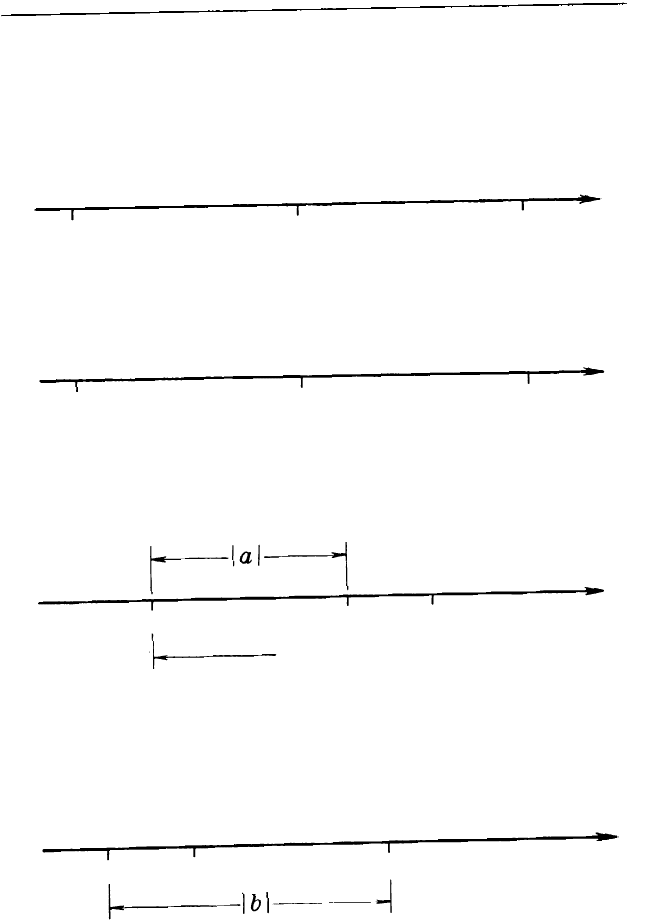
Можно

сравнивать числа и без числовой прямой по

следующим правилам:

- нуль больше любого

отрицательного числа и

меньше

любого положительного числа;

отрица

ельные числа

положительны

е числа



- любое положительное число больше любого от

ри

цательного числа;

отрицател

ьные числа

поло

жите

льные числа



- из двух

положительных чисел

больше то, у кото

рог

о бол

ьше м

оду

ль;

пол

ожител

ьные числа

1

l 

- из двух отрицательных чисел

больше то, у кото

ого м

еньше м

одуль.

ри

ельные

исла

-

�



Займемся

ением рациональных чисел. И здесь

начнем

с использования числовой прямой. Но

сначала

238

Глава четве

тая.

ациональные числа

договоримся, что все известные нам законы сложения

выполняются для любых рациональных чисел:

а +

+ а - переместительный закон сложения;

а +

(Ь

+ с)

(а

Ь) + с - сочетательный закон сло

жения;

а + О = а - свойство нуля при сложении.

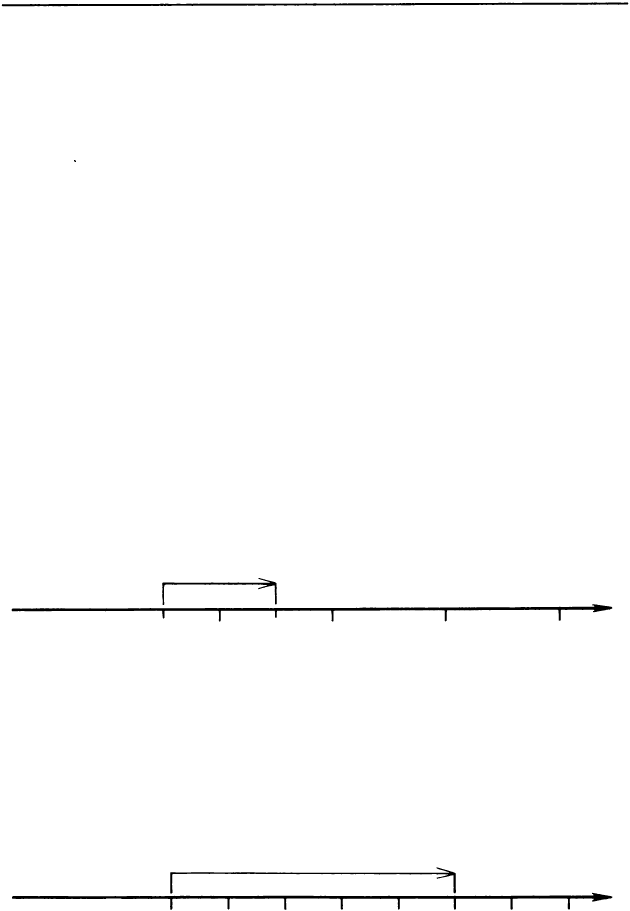
Научимся складывать рациональные числа с по

мощью числовой прямой, как уже делали это с числа

ми положительными. Тогда мы действовали так:

) отмечали на числовой прямой первое слагаемое;

2) от отмеченной точки перемещались вправо

на столько единиц, сколько их во втором слагае

мом;

3) отмечали на прямой полученную точку - это и

была сумма.

Так же можно прибавить положительное число Ь

к любому числу а (положительному, отрицательному

или нулю). Например, вот как можно найти сумму

а + Ь, если а = -2,5, Ь

\

-1,5

•

Итак, мы умеем прибавить положительное число

к любому числу. Отсюда нетрудно перейти к прибав

лению отрицательного числа к числу положительно

му: ведь слагаемые можно менять местами. Чтобы

найти, например, сумму 5 +

(

-2), достаточно найти с

помощью числовой прямой сумму -2 + 5:

-2 -1

-2 + 5

3, значит, и 5 + (-2)

239

I •

Глава четве

тая

Ра

циокалькые числа

Но можно выполнить действие 5 + (-2), и не пере

ставляя слагаемых. Чтобы понять, как это делается,

отметим на числовой прямой первое слагаемое 5 и

сумму 3:



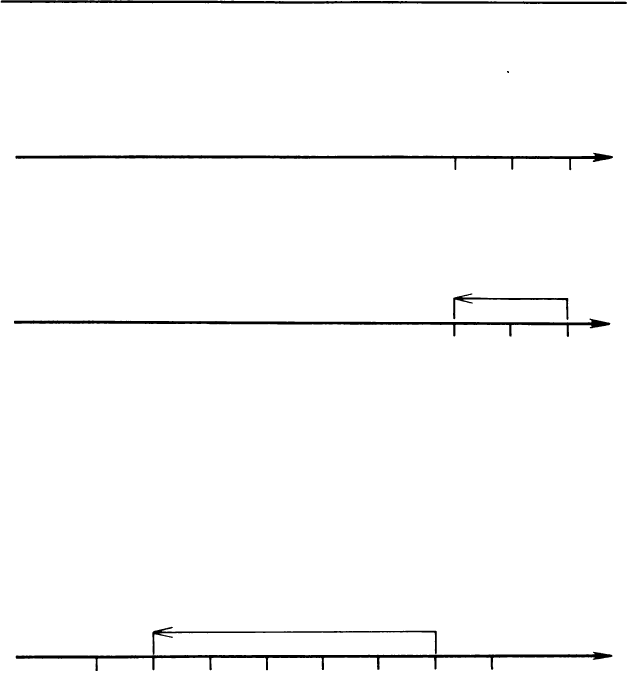
Из рисунка видно, что сумма 3 получается, если из

точки 5 переместиться влево на 2 единицы:



Значит, для того чтобы к числу 5 прибавить чис

ло -2, надо от точки 5 переместиться влево на 2 еди

ницы, то есть на столько единиц, сколько их в чис-

ле

Так же можно прибавить отрицательное число Ь

к любому рациональному числу а (положительному,

отрицательному или нулю). Вот, например, как мож

но найти сумму а + Ь, если а = -3, Ь =

-5

•

I I

- 8

-7

-6

-5

-2

Сформулируем общее правило.

Для того чтобы найти с помощью числовой прямой

сумму а + Ь, надо:

1) отметить на числовой прямой точку а;

2) указать стрелкой направление перемещения от а:

если Ь положительно - вправо,

если Ь отрицательно - влево;

3) переместиться в выбранном направлении на

столько единиц, сколько их в числе Ibl, - получим

точку, соответствующую сумме а + Ь:

240