Арутюнян Е., Левитас Г. Занимательная математика. 1-5 классы

Подождите немного. Документ загружается.

Глава четве

тая.

ацио

калькые чи

сла

Ь>О

< О

Iы1

1

1 Ь I



,Е



+ Ь

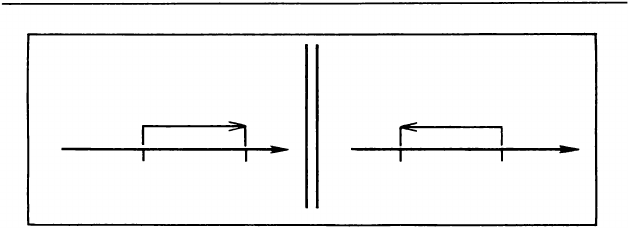
Числовая прямая позволяет понять, каким образом

надо выполнять сложение, и в тех случаях, когда изо

бразить числа трудно. Например, если надо найти сум

му чисел -3,794 и 1,6, то можно рассуждать так. Чис

ло 1,6 положительное. Поэтому от точки -3, 794 надо

передвинуться вправо на 1,6 единицы. Перейдя впра

во от -3,794 на 1 единицу, мы попадем в точку -2,794.

Перейдя вправо еще на 0,6 единиц, мы попадем в точ

ку -2,194. Следовательно,

3,794 + 1,6 = -2,194.

Еще пример: 59 +

83). Представим себе на число�

вой прямой первое слагаемое 59. Так как второе сла

гаемое

83 - число отрицательное, то направление

движения от числа 59 выбираем влево. От числа 59

нужно продвинуться влево на

-8з1, то есть на 83 еди

ницы. Так как 83 > 59, то мы перейдем через нуль, и

нам после этого останется пройти влево еще 83 - 59 еди

ниц. Итак, 59 +

83) =

24.

ло

ие

ио

аль

ны

исел

ез

омо

щи

ислово

пр

Использовать числовую прямую для сложения рацио

нальных чисел не всегда удобно. В этом легко убедиться

на примерах вроде -3,145 + 2,78 или -96 + (

)

. Поэто

му будет совсем неплохо научиться складывать рацио

ньные числа без помощи числовой прямой.

9-22

241

Глава четверт

ая

ациональные числа

Когда одно из слагаемых - нуль, то' все очень

просто:

+ О = а и О + а

а при любом значении а.

Еще один легкий случай - когда оба слагаемых

положительные числа.

Остаются только два случая:

1) оба слагаемых отрицательны;

2) слагаемые имеют разные знаки: одно положи

тельно, а другое отрицательно.

Начнем с первого случая: сложим числа -3 и -5, не

изображая их на числовой прямой, но представляя се

бе эту прямую.

Чтобы найти сумму -3 + (-5), надо от числа -3 (от

рицательного, то есть лежащего левее нуля) перемес

титься влево еще на 5 единиц. Ясно, что сумма ока

жется числом отрицательным, удаленным от нуля на

+ 5 = 8 единиц.

Значит, сумма - отрицательное чис

ло с модулем 8

-3 +

(-5) =

Вот что у нас получилось: 3 + 5 = 8 и -3 + (-5) =

Значит, е

ли

лагаемые имеют одинаковые знаки

то

их

умма имеет тот же знак

, а м

одуль

уммы

авен

умме м

одулей

лагаемых.

Осталось разобраться в случае, когда слагаемые

имеют разные знаки. Найдем, например, чему равны

следующие суммы: 1) -3 + 1;

-3 + 3

;

3) -3 + 5.

Если бы мы находили эти суммы с помощью число

вой прямой, то во всех этих случаях продвигались бы

вправо от числа -3.

В первом случае, продвигаясь от -3 на 1 единицу

вправо, мы бы не достигли нуля, а остались в левой

части числовой прямой. До нуля оставалось бы еще

3 - 1 =

2 единицы. Значит, сумма -3 + 1 - число от

рицательное с модулем, равным числу 2: -3 + 1 =

Во втором случае, складывая -3 и 3, мы продви

немся от -3 на 3 единицы вправо и окажемся в точке

О; значит, -3 + 3 = о.

242

лава че

вер

я.

ац

окалькые 

сла

в третьем случае, складывая -3 и 5, мы перейдем

через точку О и пройдем от нее вправо еще на 5 - 3 = 2

единицы. Получится положительное число с модулем

два: -3 + 5 = 2.

Сказанное можно повторить для любых чисел: е



ли

лагаемые имеют разные знаки,

но не являют

ти

вополо

жными чи

лам

и, т

о зна

к их

уммы

ов

падает

о зна

ом т

ого

лагаемого

, к

ольше по

модулю

а модуль

уммы р

авен

раз

ос

ти м

дуле

лагаемых;

умма двух п

ти

воположных

чи

ел р

ав

на нулю.

Например, 14 + (-2) - число положительное, так

как положительное слагаемое 14 имеет больший мо

дуль, чем отрицательное слагаемое -2; модуль суммы

14 + (-2) равен разности модулей слагаемых, то есть

равен 14 - 2 = 12; итак, 14 +

(

-2) = 12.

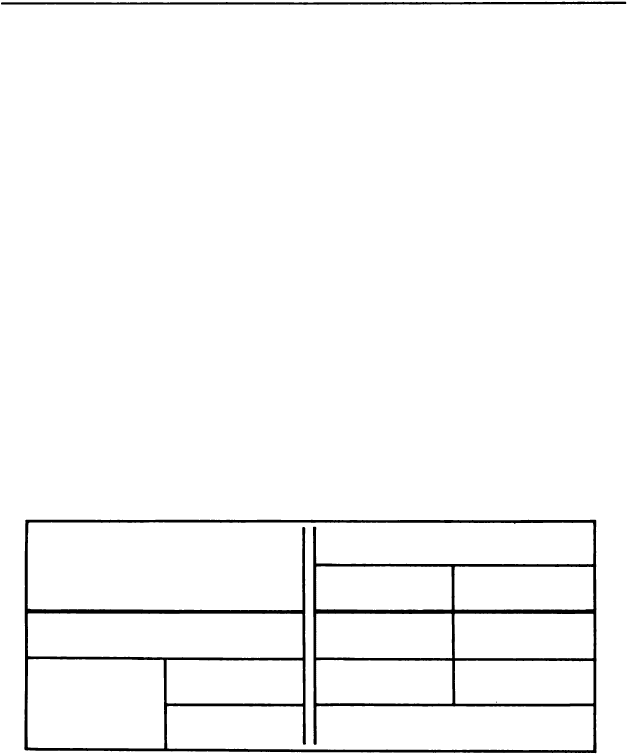
Правила сложения рациональных чисел собраны в

таблице:

Знаки

Одиновые

1> I

Разные

I а I  I Ь I

Сумма

+Ь

Знак

нак

Знак

Моду

l-lbl

+ЬО

Что нужно сделать, чтобы найти сумму с помощью

этой таблицы? Прежде всего смотрим, одинаковы или

различны знаки слагаемых. Если одинаковы - ви

дим из первой строки таблицы, что сумма имеет тот

же знак, а ее модуль равен сумме модулей слагаемых.

Если различны - сравниваем модули слагаемых. Ес

ли одно из них больше по модулю - из второй строки

таблицы находим, что сумма имеет знак того слагае-

243

Глава че

вер

ая. Р



иокалькые числа

мого, которое больше по модулю. Если модули слагае

мых одинаковы - из третьей строки таблицы нахо

дим, что их сумма равна нулю.

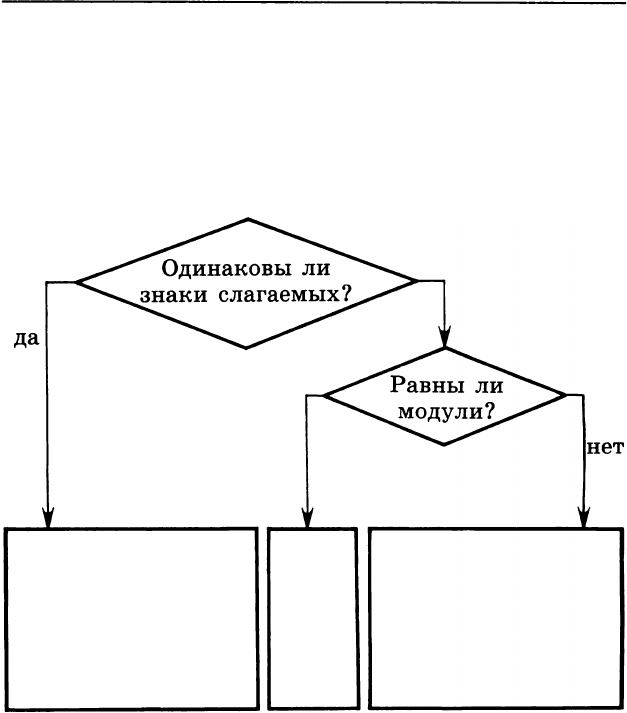
Конечно, точно так же мы действуем, если нахо

дим сумму и без всякой таблицы. Последовательность

наших действий можно представить в виде схемы:

да

3на

к суммы тот же;

Сумма

модуль равен сумме равна

модулей слагаемых нулю

нет

3нак суммы тот же,

что у слагаемого с

большим модулем;

модуль равен раз-

ности модулей сла

гаемых

ыч

ит

ан

ра

она

ьны

Чтобы научиться вычитать рациональные числа, ис

пользуем определение вычитания:

вычесть число Ь из числа а - значит найти такое

число, которое в сумме с числом Ь дает число а.

244

Глава четвертая

Рациональные чи

ла

Например, когда мы вычитаем число 2 из числа 6,

мы находим число, которое в сумме с числом 2 дает

число 6:

6 - 2 = 4, так как 2 + 4 = 6.

Пока наш запас чисел был ограничен натураль

ными числами, нулем и положительными дробями,

вычитание было возможно не всегда: нельзя было

вычесть из меньшего числа большее. Можно было от

нять пять от восьми и даже пять от пяти, но нельзя

было отнять восемь от пяти. Появление рациональ

ных чисел - великое событие: теперь вычитание воз

можно всегда.

Ведь что значит вычесть восемь из пяти? По опре

делению, это значит найти такое число, которое в сум

ме с числом 8 дает число 5:

5 - 8 = х, если х + 8 = 5.

Пока нам были известны только положительные

числа, мы не могли найти такого х. Но теперь мы зна

ем, что

-3 + 8 = 5.

Поэтому 5 - 8 = -3.

Заметим, что тот же результат мы получили бы,

прибавляя к числу 5 число -8, противоположное чис

лу 8: .

5+(-8) =-3.

Значит, 5 - 8 = 5 + (-8). Отнять от числа 5 чис

ло 8 - все равно что прибавить к числу 5 число -8.

А может быть, это всегда так? Может быть, вообще

отнять от числа а число Ь - все равно что прибавить

к числу а число -Ь?

Да, это именно так. В самом деле, равенство

а - Ь = а

+ (-Ь)

легко проверить. Для этого достаточно убедиться, что

число а + (- Ь) в сумме с числом Ь дает число а:

245

Глава четве

тая.

Ра

ЦU

Qкалькые ч

сла

(а + (-Ь» + Ь = а + « -Ь) + Ь) = а + О = а.

Мы получили правило вычитания:

Чтобы вычесть из числа а число Ь, достаточно

к числу а прибавить число, противоположное числ

а -

Ь = а + (-Ь).

Теперь мы можем любую разность записать в виде

суммы:

разность 6 -

15 - это сумма 6 + (-15),

разность 3 -х - это сумма 3 + (-х),

разность -

9 - это сумма -Ь + (

)

и так далее.

мн

ие и де

ие

ио

ны

исе

При умножении и делении рациональных чисел счи



таются справедливыми все те законы, которые изве



стны для чисел положительных:

аЬ = Ьа - переместительный закон умножения;

а(Ьс) = (аЬ)с - сочетательный закон умножения;

а(Ь + с) = аЬ + ас - распределительный закон;

•

1 = а - свойство единицы при умножении;

a·t = 1, если а � о, - свойство взаимно обратных

чисел.

На основании этих законов и законов сложения

можно доказать еще одно свойство умножения: а

•

О = о.

Вот это доказательство.

Возьмем любое число а. По свойству единицы при

умножении а = а ·1. По свойству нуля при сложении

1 = 1 + о, а значит, а = а (1 + о). По распределительно

му закону а (1 + о) = а· 1 + а· о, значит, а = а· 1 + а· о.

По свойству единицы при умножении а

•

1 = а, поэто



му а = а + а· о. Прибавим к обеим частям этого равен-

246

Глава

четвертая. Р

ациокалькые числа

ства

одно и то же число

а; получится новое

равенство

(

)

+ а = (

)

+ а + а· о.

обеих его частях содержит

ся сумма (

) + а, равная нулю по известному закону

сложения - свойству противоположных чисел. Зна

чит, это равенство можно переписать так: О = О + а· о,

то есть а· О = о, что и требовалось доказать.

Это длинное рассуждение можно переписать в виде

цепочки равенств:

= а·1 = а (1 + о) = а·1 + а· О = а + а· о, откуда

( -а

)

+ а = (

)

+ а + а

•

О, О = О + а

•

О, О = а

•

о.

Итак

, для всех рациональных чисел справедли

вы

следующие десять свойств сложения и умноже-

нмя:

1) а + Ь = Ь + а

)

а + О = а

аЬ = Ьа

а· 1 = а

а + (Ь + с) = (а + Ь) + с

а + (-

) = О

4) а (Ьс) = (аЬ) с

5) а (Ь + с) = аЬ + ас

)

а·

= 1 при а  О

)

а· 0= о.

Эти свойства применяются для упрощения вычис

лен

ий. Но еще важнее то, что с их помощью можно на

учиться

умножать и делить рациональные числа.

Дока

жем, во-первых, что числа аЬ и а (

) - про



тивоположные, то есть что их сумма равна нулю:

аЬ

+ а (-

)

= а (Ь + (-Ь» = а· 0= о.

Итак, а (

Ь) =

(аЬ).

Например, число 2· (

-3

) противоположно числу

2·

3, а значит,

2·

(

-3)

-2 ·3 =

Понятно, что и (-а)Ь = -(аЬ):

(

а)Ь = Ь (

а) =

(Ьа) =

(аЬ).

у нас

получ

илос

ь, что

произ

ведение

чисел с

разны



ми

знак

ами

это

отри

цате

льное

число,

противо

по

ложное произведению модулей множителей.

247

Глава четве

тая.

ациока



ькые

ис



Например, произведение чисел

7 и 8 - отрица

тельное число, модуль которого равен 7·8, то есть

-7 ·8 = -56.

Теперь мы умеем перемножать 1) положитель

ные числа; 2) числа с разными знаками. Осталось по

нять, как найти произведение двух отрицательных

чисел.

Для этого возьмем числа -а и -Ь. Из формул

а(-Ь) = -(аЬ) и (-а )Ь ='-(аЬ) получаем:

(-а) (-Ь) = - ((-а)Ь) = - (-(аЬ)).

Значит, произведение (-а) (-Ь) противоположно

числу -( аЬ). Например, произведение (-2) · (-3) про

тивоположно числу -(2 ·3). Отсюда получается, что

(-2) · (-3) противоположно числу -6. Но число, проти

воположное числу -6, - это число 6. Так что

(-2)

· (-3) = 6. Точно так же и вообще

(-а) (-Ь) = аЬ.

Значит, про изведение двух отрицательных чисел

положительно: оно равно произведению модулей дан

ных чисел.

Итак, чтобы найти произведение двух рациональ

ных чисел, надо:

1) найти модуль произведения: он равен произве

дению модулей данных чисел;

2) определить знак произведения: если множители

имеют одинаковые знаки, то произведение положи

тельно; если знаки разные - произведение отрица

тельно.

Так же обстоит дело и с делением:

частное двух чисел с разными знаками противопо

ложно частному модулей данных чисел; частное двух

чисел с одинаковыми знаками равно частному моду

лей этих чисел.

Например, (-14) : 7 = -2; (-15) : (-2) = 7,5 - это

легко проверяется умножением.

248

лава четве

тая.

Ра



ио

калькые чи

сла

Из правил умножения и деления полается важ

ный вывод - правило знаков:

про изведение и частное двух чисел с одинаковыми

знаками имеют знак плюс;

произведение и частное двух чисел с разными зна-

ками имеют знак минус.

Иногда, чтобы запомнить эти правила, говорят так:

Друг моего друга - мой друг; плюс · плюс = плюс.

Враг моего друга - мой враг; минус · плюс = минус.

Друг моего врага - мой враг; плюс · минус = мин

с.

Враг моего врага - мой друг; минус · мин

с = плюс.

Задач

1. а + Ь = аЬ = а Ь. Найди числа а и Ь.

2. а + Ь + с = аЬс. Найди числа а, Ь и с.

3. а + Ь + с + d + е = abcde. Найди эти числа.

4. Можно ли расставить в клетках квадрата 3х3 де

вять чисел так, чтобы сумма всех этих чисел была по

ложительна, а сумма чисел в любых дв

х соседних

клетках - отрицательна?

5. Построй как можно больше точек,

которых

1) ордината равна 3;

2) абсцисса равна -2;

3) ордината равна абсциссе;

4) ордината противоположна абсциссе;

5) ордината равна модулю абсциссы;

6) ордината противоположна модулю абсциссы;

7) абсцисса больше 2;

8) ордината меньше нуля;

) абсцисса меньше 2;

10) абсцисса больше 2, а ордината меньше 3;

11) ордината на 2 больше абсциссы;

12) абсцисса на 5 больше ординаты.

6. Будем, как обычно, обозначать абсциссу точки

буквой х, а ее ординату буквой

. Тогда условия пре-

249

лава че

вер

ая.

ациональные ис

дыдущей задачи можно переписать так: 1

)

= 3;

2) х = -2; 3)

= х и так далее. Перепиши таким обра

зом остальные задания из номера 5.

7. Вместо длинного задания «( построить как можно

болыпе точек� будем говорить кратко: �построить

графики» . Построй графики: 13

)

= х + 2, 14)

= х +

3, 15

)

У = х +

(-2), 16)

= х +

3), 17)

= 2

+ х,

)

= 3 + х, 19

)

+ 2, 20)

+ 2

, 21)

х + 2,

22)

= -

х + 3, 2

)

, 24)

= -

+ 2, 2

)

= х

- 2,

26)

= х

1, 27)

- 4, 2

)

= -

- 1, 2

)

= 2х,

)

= -

3х, 31)

�

, 32)

�

, 33)

= х2, 34) У =

= -

х2,

35)

У = х2 + 1, 36)

= х2 -

1, 3

•

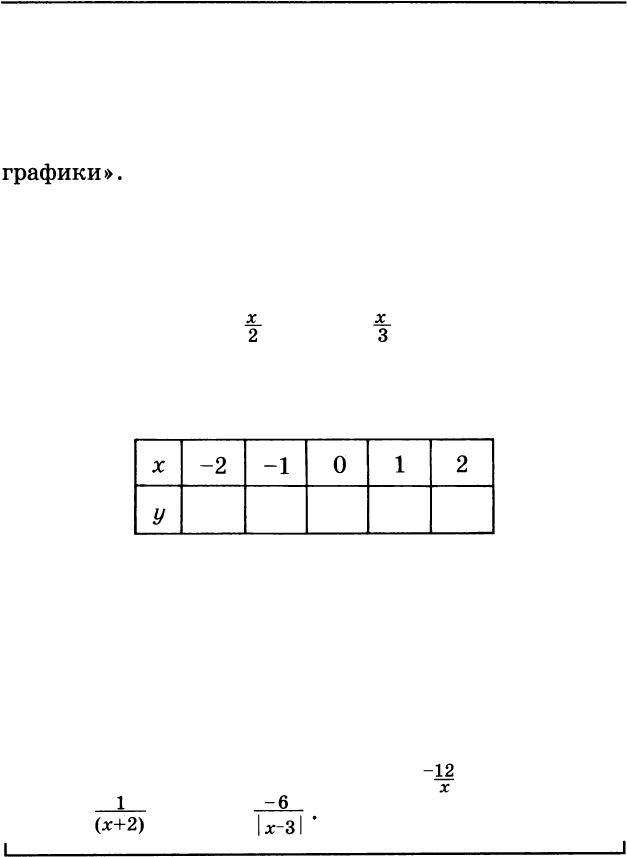
8. Следующие графики удобно строить по точкам,

заполняя такую таблицу:

I : 1-

1 О 1

1 2

)

= 2х + 1, 39

)

= 2х - 2, 40

)

= 2(х + 1), 41)

= 2(х - 1), 42)

= -2 (х

), 43)

= 2 (х + 1) - 2, 44

)

= х(х + 1) - х, 45

)

= (х + 1)(х - 1)

+ 1, 46

)

= (х +

l)х

х(х + 1) - 2(х - 1), 47)

= (х + 1)(х + 1

) -

(х

- l)

(х

1),

)

= (х + 1

)

- (х

)

х, 49

)

= 3х + 2, 50

)

= х2 + х.

9. В предыдущих задачах значение

можно было

найти для любого значения х. Следующие примеры

потр

днее:

)

�

, 5

�

, 53)

;

, 54

)

У =

)

(х1

)

, 56

)

1:�31'

'