Арутюнян Е., Левитас Г. Занимательная математика. 1-5 классы

Подождите немного. Документ загружается.

лава ше

ая. Введе



е в геометр

uю

Пирамиды известны людям давно. Несколько ты

сячелетий стоят в северо-восточной Африке пирами

ды, построенные древними египтянами. Самая боль

шая из них - пирамида Хеопса - имеет высоту око

ло 150 м. В ее основании лежит квадрат со стороной

около 230 м.

У призмы два основания, а у пирамиды одно. Вы

сотой пирамиды называется расстояние от ее основа

ния до вершины. Высоту пирамиды, как и призмы,

тоже можно измерить ростомером. Все грани пирами

ды, кроме основания, называются боковыми граня

ми - как у призмы.

Задача. На сколько удалена вершина пирамиды

Хеопса от основания - от поверхности земли?

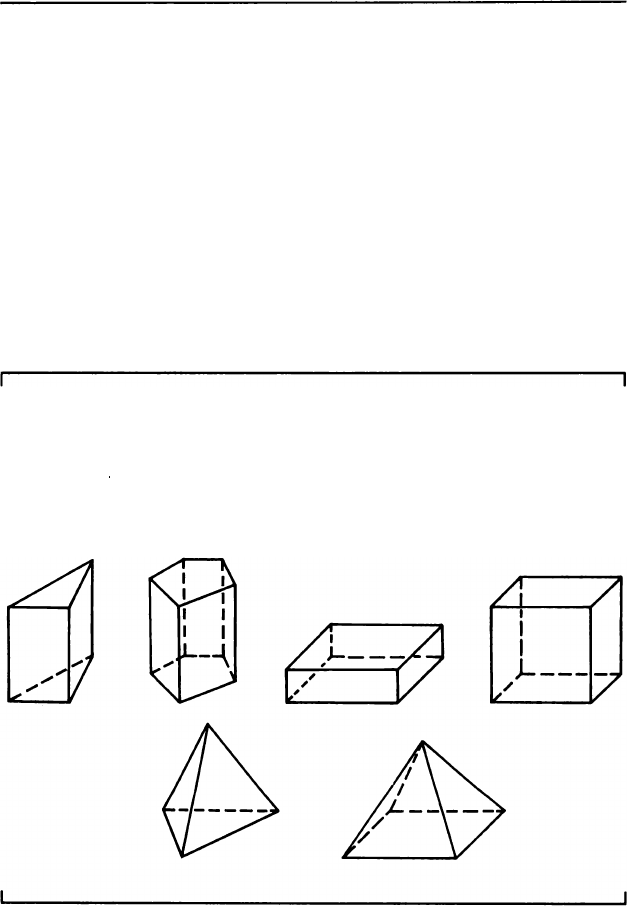
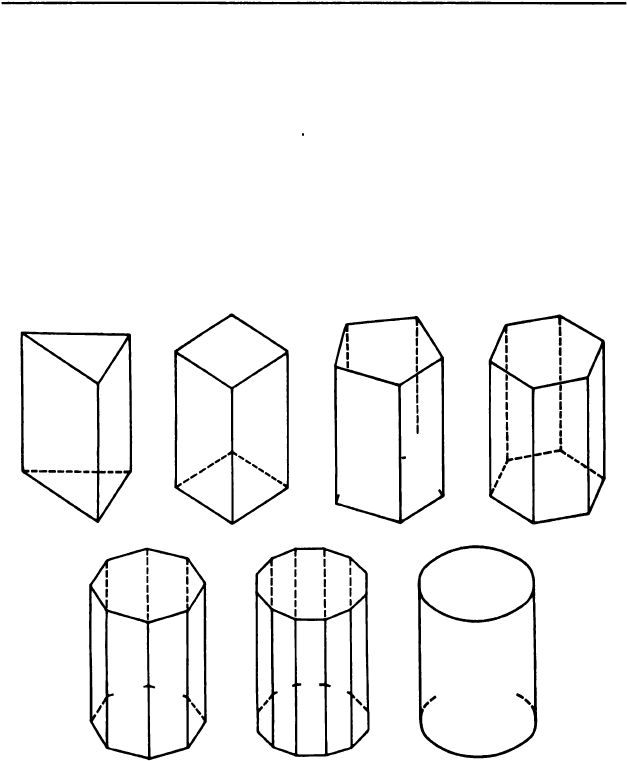
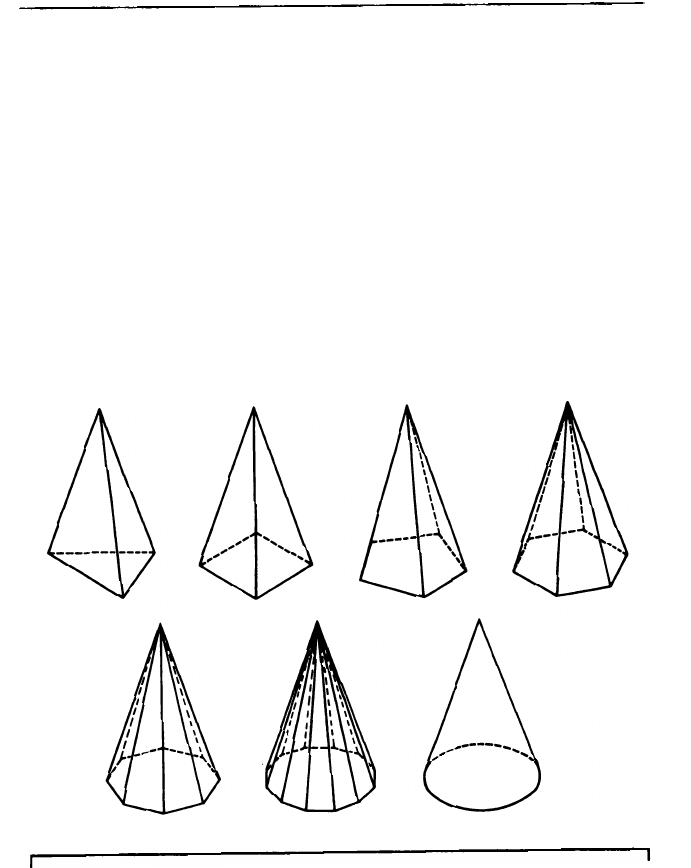
Еще задача. Среди тел, изображенных на рисунке,

найди пирамиды. Какую форму имеют их основания

и какую - боковые грани?

Но вернемся к тому, с чего мы начали наш разго

вор о пирамиде, - к вопросу о ее объеме.

271

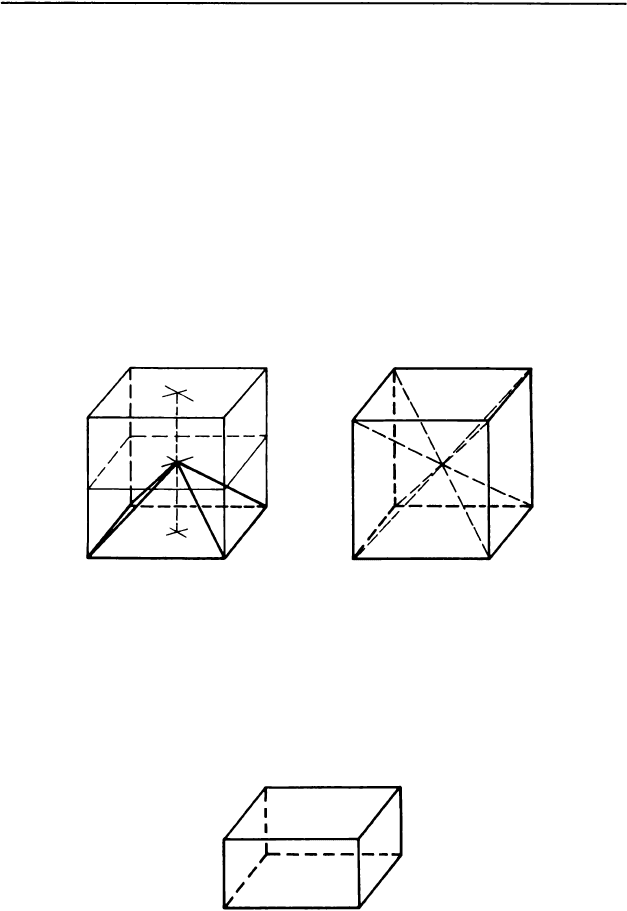
Глава ше

ая. Введекие в геометрию

Возьмем пирамиду и призму, У которых равны и

основания, и высоты. онечно, объем такой пирами

ды меньше объема такой призмы. Но оказывается -

не просто меньше, а меньше ровно в три раза.

Доказательство этого очень сложно, и о нем гово

рить мы не будем. Но есть один пример, который

прост и понятен.

Возьмем куб. Соединим его центр со всеми точками

нижнего основания куба. Получится пирамида. Та

Kиx пирамид в кубе шесть. Все эти пирамиды равны

друг другу, а значит, имеют равные объемы. Объем

каждой из них равен i части объема куба.

Теперь рассмотрим прямую призму с таким же ос

нованием и с такой же высотой, как у построенной на

ми пирамиды. Эта прямая призма - половина куба.

Ее объем равен половине объема куба. Итак, объем

пирамиды в нашем случае действительно равен t объ

ема призмы с таким же основанием и с такой же вы

сотой.

Поэтому коробку в t литра можно сделать в виде

пирамиды, у которой основание и высота такие же,

272

Глава ше

стая. Введекие в геометрию

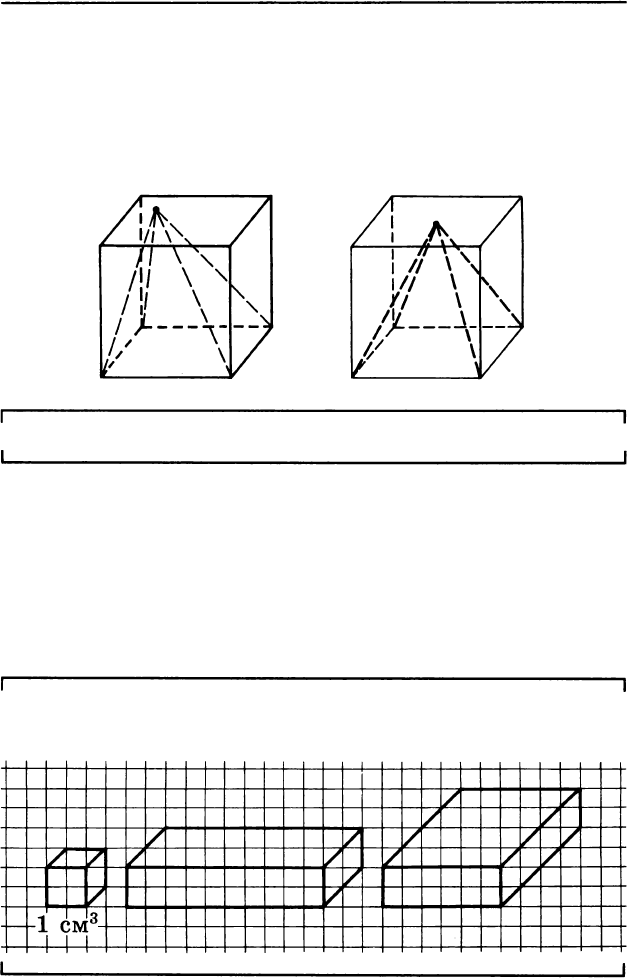
как у литрового куба. В качестве основания берется

нижнее основание такого куба, а в качестве верши

ны - любая точка на верхнем основании куба. У доб

нее всего взять в качестве вершины центр верхнего

основания. Объем этой пирамиды втрое меньше объе

ма этого куба, то есть равен

литра.

Задача

Склей пирамиду объемом в

литра.

улы об

ъема

при

змы

и пи

миды

До сих пор речь шла о том, как склеить призму или

пирамиду известного объема. А если нам дали гото

вую призму или пирамиду - как измерить их объем?

Начнем с призмы. Как узнать, сколько в ней поме

щается единиц объема - единичных кубиков?

Задача. Найди площадь основания и объем каждо

фигуры на рисунке.

 



 

 7



 /



� ��3

10-22

273

Глава

ая. Введеки

е в геометрию

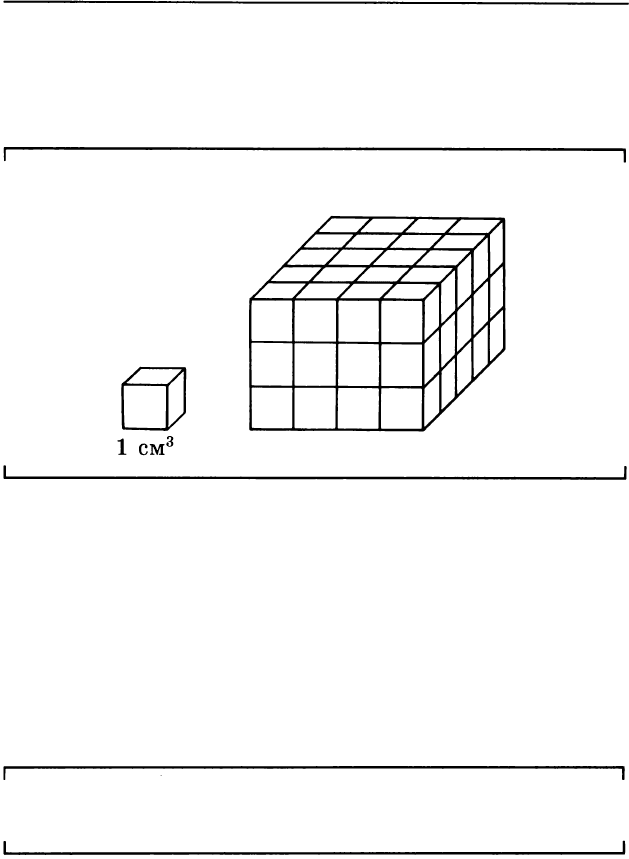
Как видно, в одном слое помещается столько куби

ков, сколько квадратных единиц помещается в осно

вании. Это означает, что если высота призмы равна 1,

то ее объем численно равен площади основания.

Задача. Найди площадь основания и объем фигуры

на рисунке.

 / /

/ /



/ /

/ / / /

;



Получается, что объем равен произведению числа

единичных кубов в одном слое на число слоев. Объем

обычно обозначают буквой V, а площадь основания -

буквой S

А так как число кубиков в одном слое равно

площади основания, а число слоев равно высоте пря

мой призмы, получаем такую формулу:

V= Sh,

где V - объем призмы, S - площадь ее основания,

h - ее высота.

Задача. Сколько слоев единичных кубов содержит

ся в прямой призме с высотой 3 единицы?

Формулой объема можно пользоваться лишь тог

да, когда площадь основания и высота измерены в со

ответствующих единицах, например в квадратных

сантиметрах и сантиметрах. Тогда и объем получает-

274

ла

а ше

я. Введек

е в геометрию

ся в соответствующих им единицах, например в куби

ческих сантиметрах.

Задача. Вычисли объем прямой призмы с площа

дью основания S и высотой h, если 1) S = 5 см

, h =

4 см; 2) S

7 м

, h

8 м; 3) S

6 дм

, h = 4 м.

Теперь возьмем пирамиду с основанием, площадь

которого равна S, и высотой h. Ее объем V в три раза

меньше, чем объем призмы с такими же основанием и

высотой.

Задача. Объем пирамиды равен 660 см3• Определи

объем призмы с таким же основанием и такой же вы

сотой, как у этой пирамиды.

Формула объема V пирамиды с площадью основа

ния S и высотой h получается такая:

зSh.

Задача

Вычисли объем прямой пирамиды с пло

щадью основания S и высотой h, если 1) S = 5 см

4 см; 2) S = 7 м

, h

8 м; 3) S

6 дм

, h

4 м.

Еще задача

Из склеенных раньше фигур возьми

одну призму И одну пирамиду и вычисли их объем.

Выполняй работу в таком порядке:

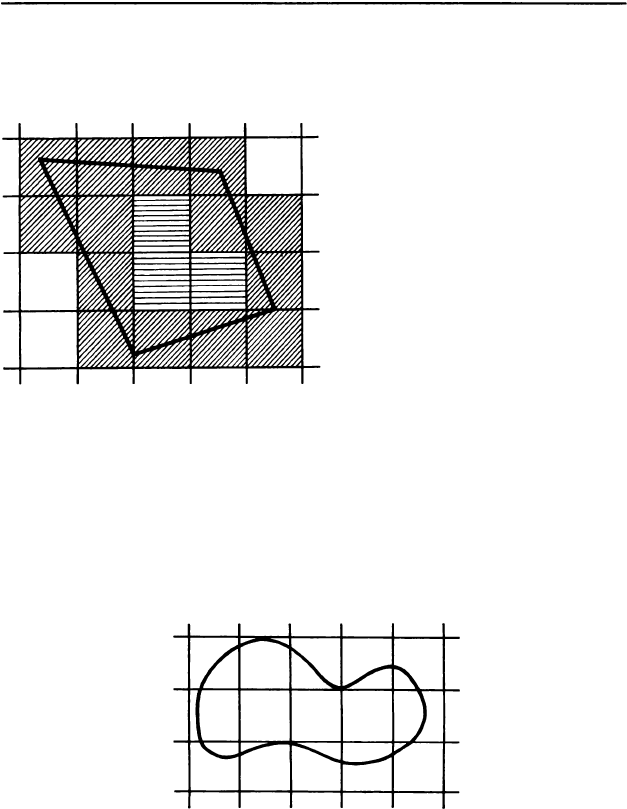
1) Начерти сетку с квадратами в 1 см, поставь на

нее основание призмы или пирамиды и обведи его ка

paHдaшoM. Квадраты, целиком содержащиеся внут

ри нарисованной фигуры, заштрихуй горизонтально

(на рисунке имеется 3 таких квадрата). Квадраты, за

нятые этой фигурой частично, заштрихуй косо (

на

рисунке имеется 14 таких квадратов). Подсчитай

приблизительно площадь фигуры, считая площадь

275

Глава ше

ая

Введение в геометрию

каждого квадрата, заштрихованного горизонтально

за 1 см2, а площадь каждого квадрата, заштрихован

ного косо, за

см2•

222

2 2 2 2 2 2

2 2 2 2 2

2) Измерь высоту призмы или пирамиды.

3) Вычисли объем, подставив в нужную формулу

найденные значения площади основания и высоты

призмы или пирамиды.

Еще задачи

1. Вычисли по клеткам приблизительную площадь

фигуры на рисунке.

2. Вычисли объем пирамиды Хеопса (см. с. 271).

3. Объем пирамиды равен 150 дм3• Чему равен объ

ем прямой призмы с таким же основанием и такой же

высотой, как у этой пирамиды?

4. Объем прямой призмы 72 см3, а площадь ее осно

вания равна 18 см2• Чему равна ее высота?

276

Глава шес

ая. Введени

е в геометрию

5. Объем пирамиды равен 48 см3, а ее высота 30 мм.

Чему равна площадь ее основания?

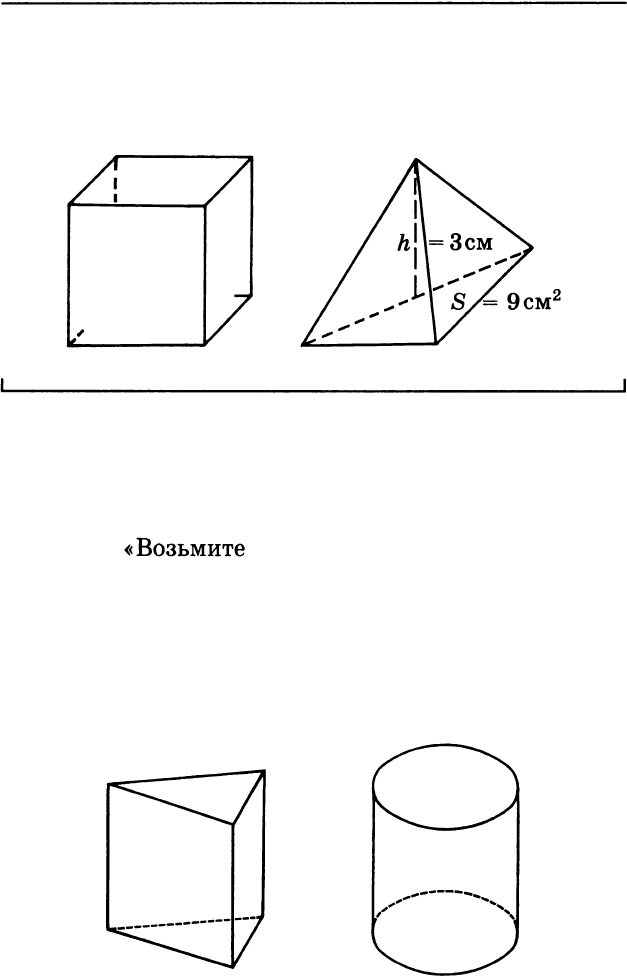
6. На рисунке изображены сосуды. Сколько жид

кости вместится в этих сосудах?

/h=3cM

-- ----

= 9

см

Ци

ир

Объем часто измеряют стаканами. Так и пишут в

рецептах: «Возьмите

два стакана муки».

Обычный круглый тонкостенный стакан. имеет

объем i литра. Форма такого стакана - цилиндр.

Из всех фигур, о которых мы говорили, больше

всего похожа на цилиндр прямая призма. Только осно

вания у призмы - многоугольники, а у цилиндра -

круги.

277

лава ше

ая. Введе



ие в геометр

Формула объема прямой призмы V = Sh верна и

для цилиндра. И ничего удивительного в этом нет.

Представим себе, что мы стали увеличивать число

сторон многоугольника, лежащего в основании п

я

мой призмы: взяли треугольную призму, от нее пере

шли к четырехугольной, потом к пятиугольной и так

далее. В конце концов мы не сможем отличить м

о

угольник от круга и призму от цилиндра. А формула

V = Sh, верная для всех этих призм, в конце концов

перейдет в формулу объема цилиндра.

 --.

�----_. -�,

' -- 

V= Sh

; . -----,

Найдем по этой формуле вместимость стакана,

внутренние размеры которого такие: площадь основа

ния равна 28,8 см

, а высота 8,7 см. По формуле объ

ема получаем:

V = Sh = 28,8 ·8,7 = 250,56 (см3).

278

Глава шестая. Введек

е в геометрию

Задача. Найди объем цилиндра, высота которого

равна 3 м, а площадь основания 36 дм2•

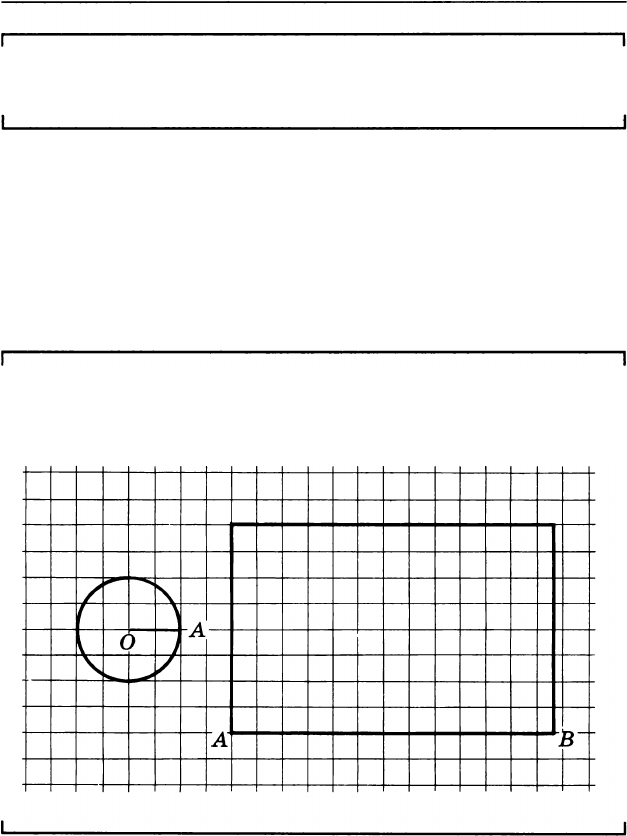
Чтобы склеить цилиндр, вырезают два равных

круга и прямоугольник, который можно свернуть

так, что получится стенка цилиндра. Правда, пра

вильно подобрать длину этого прямоугольника непро

сто. О том, как это делается, мы будем специально го

ворить. А пока что склей цилиндр, точно копируя ри

сунок.

Задача. Склей цилиндр по рисунку и вычисли его

объем, измеряя площадь круга по клеткам, как в за

даче на с. 275.

/ 







п-

ну

Как изготовить сосуд, объем которого в 3 раза меньше

объема стакана? Конечно, можно склеить цилиндр

279

Гла

а шестая

. Введеки

е в гео

ме

рию

с таким же основанием и с высотой, в 3

аза меньше

Но можно поступить и так, как мы однажды поступи·

ли с п

измой, - пе

ейти к фигу

е д

угой фо

мы:

от п

измы - К пи

амиде,

от цилинд

а - к конусу.

авним фо

мулы:

V п

измы

V цилинд

V пи

амиды

!Sh,

V конуса

Sh.

Нет ничего удивительного в том, что фо

мулы объе

ма пи

амиды и конуса одинаковы. Ведь конус можно

едставить себе как пи

амиду , в основании кото

ежит многоугольник с бесконечно большим числом

сто

он.

Задача. В цилинд

вставили конус с таким же ос·

нованием и такой же высотой, как у цилиндра. Какая

часть объема цилинд

а занята конусом? Какая часть

свободна от конуса?

280