Аскирка В.Ф. Электричество и магнетизм. Волновая оптика

Подождите немного. Документ загружается.

231

(

)

BlEnnlL

=-=D . (22.25)

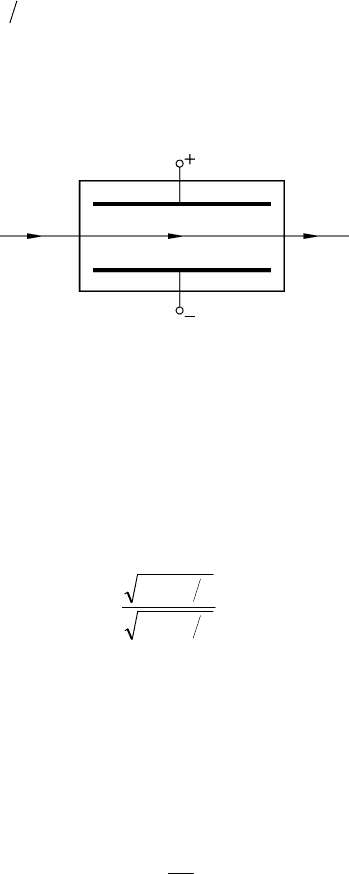
Величина l= kB называется постоянной Керра. Для наблюде-

ния эффекта Керра используется ячейка Керра, которая представ-

ляет собой сосуд с жидкостью с прозрачными плоскими стенками.

В жидкость помещаются пластины плоского конденсатора, к ко-

торым подается высокое напряжение (рис. 2.41).

Оптический эффект Доплера – изменение частоты колеба-

ний или длины волны, воспринимаемой наблюдателем, при дви-

жении источника (излучающего атома) и наблюдателя друг отно-

сительно друга. Выделяют поперечный и продольный эффекты

Доплера.

Продольный эффект Доплера наблюдается при относитель-

ном сближении или удалении источника или приемника. В этом

случае частота волны, регистрируемая наблюдателем, будет равна:

u±

n=n

, (22.26)

где

n – частота излучения неподвижного источника,

– ско-

рость света в вакууме, где

u – проекция скорости движения ис-

точника или наблюдателя на направление, соединяющее источник

и наблюдателя (рис. 2.42).

Если скорость движения источника (приемника) значительно

меньше скорости света в вакууме (

), то выражение (22.26)

будет иметь вид:

n»n

. (22.27)

Рис. 2.41

232

Знак «+» соответствует движению частицы к наблюдателю, а «-» –

от наблюдателя.

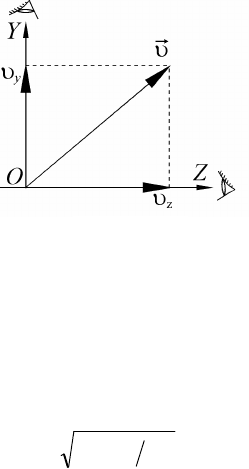
Поперечный эффект Доплера наблюдается при движении

источника света в направлении, перпендикулярном линии, соеди-

няющей источник с наблюдателем. Частота

, регистрируемая

наблюдателем, будет определяться выражением:

(

)

1 c

u-n=n , (22.28)

где

u – проекция скорости движения источника или наблюдателя

на направление, перпендикулярное линии, соединяющей источник

и наблюдателя (рис. 2.42).

Необходимо отметить, что поперечный эффект Доплера зна-

чительно менее выражен, чем продольный.

Рис. 2.42

233

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. В упругой среде распространяется плоская попе-

речная волна, имеющая частоту

102,1 × Гц и амплитуду колебаний

1,2 мм. Определить длину волны, фазу колебаний, смещение, ско-

рость и ускорение точки, расположенной на расстоянии 30 см от

источника в момент времени 0,15 мс, считая начальную фазу рав-

ной нулю. Определить разность фаз колебаний двух точек, распо-

ложенных на расстоянии 40 см и 42 см от источника. Плотность

среды принять равной 2700 кг/м

, модуль поперечной упругости

(модуль сдвига)

105,2 × Н/м

Дано:

102,1 ×=n Гц,

2,1

=y мм

102,1

×= м,

x см 30,0

м,

15,0

t мс

1051

×= , с,

=x см 40,0

м,

=x см 42,0

м,

2700

кг/м

105,2 ×=G Н/м

Найти:

Решение. В соответствии с [14.5] длина волны равна расстоя-

нию, которое проходит волна за время, равное периоду:

. (1)

Скорость распространения волн, являющихся по условию задачи

поперечными, определим из условия [14.17]:

. (2)

Поскольку период и частота связаны между собой соотношением

[14.3]

/1T , то на основании выражений (1) и (2) имеем:

. (3)

234

Подставляя числовые значения, получим:

250

2700

1052

1021

=l м.

Для определения других характеристик волны запишем ее

уравнение [14.4]:

(

)

kxtyy -w= cos

, (4)

где

y – амплитуда,

– циклическая частота, k – волновое чис-

ло,

– расстояние от источника до данной точки.

Как известно, в уравнении волны выражение, стоящее под

знаком косинуса, является фазой волны

[14.2] и определяя-

ется как

kxt

. (5)

С учетом выражений, связывающих циклическую и линейную час-

тоты [14.3], а также, используя определение волнового числа

[14.4], перепишем (5) в виде:

(

)

l-np=F xt2 .

Поставив числовые значения, получим:

(

)

p=-×××p=F

2,125,030,0105,1102,12

Величину смещения определим, подставив в уравнение (4)

значения фазы и амплитуды:

(

)

107,92,1cos102,1

×-=p×=y м 97,0

мм.

Скорость движения частиц среды равна первой производной

смещения по времени:

=u .

Дифференцируя (4), имеем:

(

)

(

)

[

]

l-nppn-=-ww-=u xtykxty 2sin2sin

. (6)

Выполняя вычисления, получим:

-×××p×××××-=u

25,0

30,0

105,1102,12sin102,1102,114,32

4434

253,

м/с.

Ускорение является первой производной по времени от ско-

рости, поэтому, дифференцируя (6), получим:

235

(

)

(

)

(

)

l-npn-=-ww-= xtykxtya cos2cos

После подстановки числовых данных получим:

()

-×××p××××-=

25,0

30,0

105,1102,12cos102,114,32102,1

1026 ×= , м/с

Для определения разности фаз колебаний для точек с коорди-

натами

x и

x воспользуемся соотношением (5):

()()

1212

xxxxk -

=-=DF .

Подставив заданные в условии задачи значения, получим:

()

p=-

=DF 16,040,042,0

25,0

Ответ: 25

см,

2,1 , 970,y

мм, 253,

м/с,

160, ,

1026 ×= ,a м/с

Пример 2. Определить время, через которое повысится тем-

пература стакана воды массой 0,50 кг на 1,0 °С при условии по-

глощения всей энергии падающей звуковой волны, имеющей уро-

вень громкости 70 дБ. Поглощающая площадь стакана 50 см

. Те-

плоемкостью стакана, а также теплообменом стакана с окружаю-

щей средой пренебречь. Минимальная интенсивность звука, вос-

принимаемая органом слуха человека,

100,1

×=I Вт/м

Дано:

L дБ,

S см

2 3

1005

×= , м

0,1

T °С,

50,0

m кг.

Найти:

Решение. Уровень громкости, выраженный в децибелах (дБ),

определяется выражением [15.1]:

236

lg10

L =

, (1)

где

– интенсивность данного звука,

I – минимальная интен-

сивность звука, воспринимаемая органом слуха человека.

Из соотношения (1) получим:

или

(

)

1,0

10= . (2)

Подставляя числовые значения в (2), имеем:

5701,012

100,110100,1

-×-

×=××=I Вт/м

Определим энергию, поглощенную стаканом воды площадью

S за время

IStW

. (3)

Энергия, необходимая для того, чтобы температура заданного

количества воды увеличилась на

=1,0 °С, будет определяться

выражением:

TcmQ

, (4)

где

– удельная теплоемкость воды,

– ее масса.

Поскольку вся энергия звуковой волны идет на нагревание

воды ( QW

), то из соотношений (3) и (4) легко определить вре-

мя, необходимое для нагревания воды:

Tcm

== .

Подставив числовые значения, получим:

102,4

1050100,1

0,150,04200

×=

×××

××

с.

Ответ:

102,4 ×=t с.

Пример 3. Резонатор, настроенный на частоту 15 кГц, при-

ближается к источнику звука, излучающему акустическую волну

длиной 2,5 см. С какой скоростью должен двигаться резонатор,

чтобы в нем возникли колебания? Температура воздуха 27 °С.

237

Дано:

15=n

рез

кГц

1051 ×= , Гц,

5,2

=l см

1052

×= , м,

t °С, 300

T К.

Найти:

u .

Решение. Как известно, вследствие эффекта Доплера, при от-

носительном движении источника и приемника звука частота n

регистрируемая приемником, будет отличаться от частоты источ-

ника

n . Количественно эта зависимость выражается соотношени-

ем [15.6]:

u-u

n=n

, (1)

где

– скорость звука в среде,

u и

u – скорости источника и

приемника соответственно. В условиях задачи источник неподви-

жен ( 0=u

), поэтому выражение (1) запишется в виде:

+n=

u+u

n=n

пп

. (2)

Скорость звука в газе зависит от температуры и молярной

массы газа [15.5]:

g=u , (3)

где

– универсальная газовая постоянная,

– абсолютная тем-

пература,

– молярная масса,

– показатель адиабаты, равный

отношению молярной теплоемкости при постоянном давлении к

молярной теплоемкости при постоянном объеме:

. (4)

Учитывая, что

lu=n , а также соотношение (3), запишем (2) в

виде:

u+g

. (5)

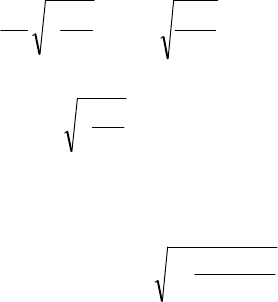
238

Условием возникновения колебаний в резонаторе является равен-

ство частоты излучения источника, приходящего к резонатору, и

его собственной частоты:

рез

n=n

. (6)

На основании равенств (5) и (6) получим:

u+g

през

Откуда искомая скорость резонатора выразится так:

резn

g-nl=u

. (7)

Принимая для воздуха 4,1

(считаем его двухатомным газом),

молярную массу 029,0

M кг/моль и подставляя числовые значе-

ния других величин, получим:

1092

300318

4110511052

-×××=u

,,,

м/с.

Ответ: 28=u

м/с.

Пример 4. Определить частоту колебаний столба воздуха в

трубе длиной 1,12 м при температуре воздуха 27 °С. Рассмотреть

случаи, когда труба открыта с обоих концов; труба закрыта с обо-

их концов; один конец трубы закрыт, а второй – открыт.

Дано:

12,1

l м,

t °С; 300

T К.

Найти:

Решение. В трубе (или стержне) происходит отражение коле-

баний на концах. При этом значительную амплитуду будут иметь

только те колебания, для которых в трубе образуются стоячие

волны.

Если труба с обоих концов будет закрыта, то на концах будут

образовываться узлы; если же труба открыта с обоих концов, то на

239

концах будут образовываться пучности. В обоих случаях условие

образования стоячих волн будет иметь вид:

l , (1)

откуда

=l , (2)

где

– натуральное число.

Для определения частоты колебаний воспользуемся соотно-

шением между частотой, скоростью распространения и длиной

волны [14.3], [14.5]:

=n . (3)

Будем считать воздух в трубе идеальным газом. Тогда, под-

ставляя в соотношение (3) выражение для скорости звука в иде-

альном газе [15.5], получим:

g=n

. (4)

Максимальную амплитуду будут иметь колебания так называемой

собственной частоты (основной тон), получающиеся при 1

т . С

учетом этого, соотношение (4) примет вид:

g=n

. (5)

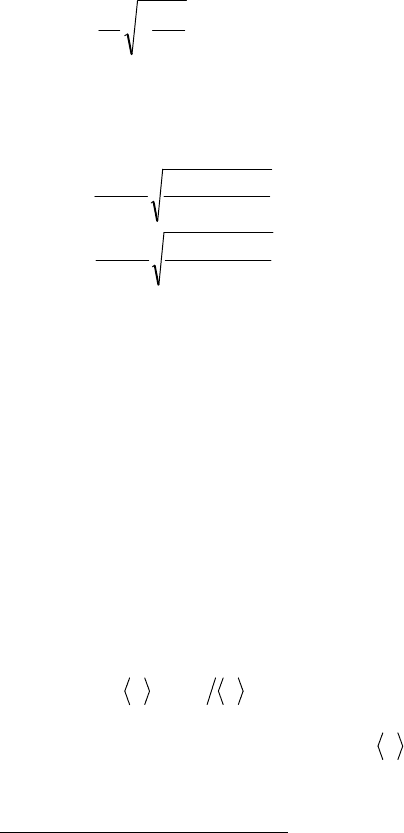
Если один конец трубы закрыт, а второй – открыт, то со сто-

роны закрытого конца будет образовываться узел, а со второго

конца, открытого, будет образовываться пучность. Условие обра-

зования стоячих волн будет иметь вид [14.14]:

()

-= тl . (6)

Проделав аналогичные предыдущему случаю выкладки, получим

выражение для частоты:

. (7)

Положив 1

т , определим основную частоту колебаний:

240

g=n

. (8)

Принимая для воздуха показатель адиабаты равным 1,4 (считаем

его двухатомным газом), а молярную массу воздуха 0,029 кг/моль,

подставляя числовые значения других величин в (5) и (8),

получим:

155

0290

30031841

1212

××

Гц,

477

0290

30031841

1214

××

=n Гц.

Ответ: 155

=n Гц, 4,77

=n Гц.

Пример 5. Точечный изотропный источник, имеющий силу

света

J , расположен на высоте

над серединой круглого стола

радиуса

. Определить: а) среднюю освещенность стола; б) во

сколько раз средняя освещенность стола меньше максимальной;

в) высоту, на которой следует расположить источник, чтобы ос-

вещенность на краю стола была максимальной; г) кривую свето-

распределения

, которую должен иметь источник, чтобы освещен-

ность стола была равномерной.

Дано:

J ,

Найти: E , EE

max

, h ,

(

)

J .

Решение. Средняя освещенность E равна отношению све-

тового потока, падающего на некоторую площадку, к величине

площади этой площадки [17.2]:

Кривая светораспределения – это построенная в полярных координатах

зависимость силы света источника от угла

(

)

jJ , образуемого направле-

нием, соответствующим максимальной силе света

J , и данным направ-

лением.