Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

290 Гпава 7

Дифференцируем еще раз по у

х"

—

(-((x'sin

(^>^)+

Jccos {y^y^ip^'y + л:))(2х+

>^sin

(-^З^))

—

-x'^m{xy^{lx л-%т{ху^^ |.

д) Дифференцируем обе части по х

3x^+3//

О,

откуда / = -

Дифференцируем еще раз по х

ху

х — ^

^ У у' / ;^^

Для нахождения j;'"дифференцируем еще один раз по х

,„_

, (/ +хуУ+4х^)У -5(У

+^'^)//

/ /

е) Дифференцируем обе части по у

jc4l

^ = J7 ^' откуда

cos (x-fj;)

1 cos^(x +

3;)

_ 1

cos^

С^ +

З^)

cos^ (x +

j;)-!

sin^

(•^

>^)

Дифференцируем еще раз по у

.^^cos(x

>^)(x4l)__ ^cos'(x +

j;)

sin {хл-у) sin^(x +

>^)'

Дифференцируя еще раз

по>^,

окончательно получим

x"' = -2(-3cos'(x

j;)sin^(x

+ >;)(x4l)-cos'(x +

j;)-

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ

291

•5sin^(x4-j;)cos(jc + ;;)(x4l))/(sin'^(jc

;;)) =

(Зsin^ [хЛ-у)

5cos^

(jc

j^))cos"^

{^^У)

= -2((3 + 2cos^(jc +

>^))cos'^(x

>^))/sin^(x

>^).

3.3.

Найти производные указанных порядков:

а)

в)

x=cos

>'=sin

2<Р

^•7

(fx.

б)

rx = 2cos/-cos2/,

Д),._

dy'' г)

f-i

.з?е)

[x = arcsin/,

Решение, а) Найдем первую производную

dx х\

/ +1

Вторую производную находим по формуле

21п^

dx^ х\

1п/

б) Первая производная равна

dy _у\ _

2 cos

(ln/ + l)

cos 2/

dx x\ -2sinr + 2sin2/ sin

2/-sin

Вторую производную находим по формуле

dx"-

d/-

292 Гпава 7

d^y _ ух-'ху _

-4 sin It (-2 sin / +

sin It)- (-2

cos

+ 4

cos

2/)

2 cos

It _

(-2sin/

+ 2sin2/)^

_ 2sin/sin2/ + cos^cos2/-2

(sin

2^-sin/)

в) Находим первую производную

Ф • Ф 1

, ' -2cos—sm-^^—

d^ ^\ ^ 2 22^^

dy у о • Ф Ф 1

-^ ^^ 2sin

—cos—

2 2 2

Вторая производная равна

Л_(^^)^

_ О

= 0.

dy^ у о • Ф Ф i

^ ^^ 2sin—cos— -

2 2 2

г) Первая производная

d:x^2^-^ln2^2^in2

Ф^~

1.2/ "" ^

Вторая производная будет

, 2Чп^г-2Чп2

d'yJy'X

^ t' ^

2-1п2(/1п2-1)

dx'

У: t_ е

д) Находим первую производную

dy yl acoscp

dx X -a sm

ПИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

293

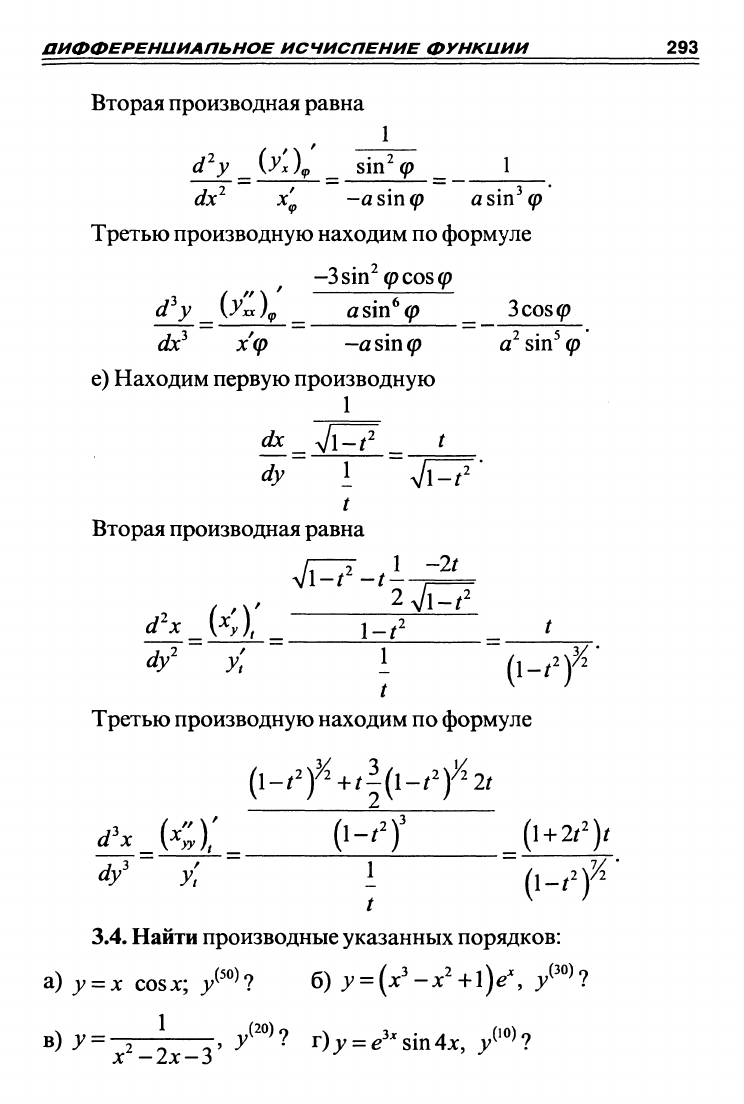
Вторая производная равна

d^y

^{УхХ ^

sin>

^ 1

Третью производную находим по формуле

-3sin^^cos^

asin^q) 3cos^

dx^

x(p

-asin^

^хих"

e) Находим первую производную

y/l^t^

^ t_

1 VlT

Вторая производная равна

4^-

' -2'

•t

d'xiK)!

24)^

\-e

y. 1

{x.t'f

Третью производную находим по формуле

d/ У. 1

(1_,ПК

3.4.

Найти производные указанных порядков:

а)

cosx;

/-)? б) у

{х'-х'+\)е\

/"^

в) У=^2_\^_^^ /"^? r);; = e^^sin4x, /"^ ?

294 Гпава 7

2х+3

д)>;

1п(2х

1),

у-)? €)У=^^^, ГЩ^.

Решение, а) Положим и-х^,

£;

= cosx. Тогда

= 2x,

л:.

По формуле Лейбница

все

слагаемые,

кроме трех последних,

равны нулю, поэтому получаем

.л:

х+49^

l+x^cos jc+50~ 1=

/«) =i50-49cos( jc+48-|+50'2хсо8

= (l 225 - jc^) cos jc -1

OOJC

sin X.

6) Положим

= e'', t; = x^~x^+l. Тогда i;' = 3x^-2x5

t;" = 6x-2,

u*"

= 6, t;^'^=u(^>=... = 0, w^''^ =e". По формуле Лей-

бница все слагаемые, кроме четырех первых, равны нулю. Та-

ким образом,

/^)=^-(х^-хЧ1)

30е^(Зх^-2х) + ^^^е^(6х-2) +

^30-29-28^,^^^,^^3^gg^2^2550x + 2348l).

в) Преобразуем выражение к виду

1 \( 1

у-

(х-3)(х+1) 4

Так как

Чп)

уХ-Ъ)

(-!)"«!

(х-3)

п+1 и

х-3 x+l

( 1 Г _

(-!)"«!

U + lJ

^х-МГ'

ТО

(20) 1

// .ч20

20 ^л,

(-If

20!

(-1^20!

[ (x-3f " (x+lf J

20!

\{х-ЪТ (x+lf

ДИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКиИИ

295

г) Полагая в формуле (8) а-Ъ,

Ь =

4, будем иметь

^(lu; =

(3^

+ 4^

^зд^

sin(4x

+10(р),

где sin

ср

/^>=5^V^^sin

4jc

+ 10arcsin

. 4^

л/зЧ4^'

или

д) Находим первую производную у'

. Рассматривая

х +

первую производную как функцию от х, находим {п~1) произ-

водную по формуле (2,а; пункт 5°)

( 2

f-'^_{-iy~\n-l)\r

+ 2х

2хУ

Таким образом,

\39^^,^39

+ 2х)

\39

+ 2х

е) Запишем выражение в виде у{х){х^-х

+ 6) =

2х

+ 3

и,

применяя формулу Лейбница, продифференцируем п раз. При

п>2 будем иметь

/"\х'--х +

+ п/"-'\2х-1) +

^^^^^^

откуда при х

0 получим

6/"^

(0)

п/''-'^

(0)

+ «(« -

\)/"-^^

(0) =

i")rn\ ^ («-О/ЛЧ '^(^"•^) (n-2)/^4

о 6

Полученная рекурентная формула, позволяет определить

П'Ю

производную в точке х

0 (п>2). Значения у (0) и ;;' (0)

находятся непосредственно

296

Гпава

Я0)=|

/(0) =

~2X^-6JC

+ 15

(jc^-x + б)

36*

ijc=0

Полагая последовательно п - 2,3,4,...,

помощью рекурен-

тной формулы находим значения искомых производных. Так

/'(0)

±/(0)-i-i>;(0)

-''''

/"(о)=|/'(о)-^У(о)=^''

_1_

36'

215

.11

ТА.

Дифференциал функции

^у

1°.

Из определения производной

птд^_^о

—

y\i предела

Дх

Ау , ,

переменной следует, что —-у л-а или

Д>;

= >;Дх

аДх, где

Ах

а ->

при Ах ->

О,

т. е. приращение функции можно разбить на

две части.

Произведение j;'Ax есть бесконечно малая первого поряд-

ка относительно

Ах.

Произведение

же

оАх есть величина беско-

нечно малая высшего порядка относительно Ах, т.к.

Первое слагаемое приращения функции называется глав-

ной частью

приращения.

Произведение j;'Ax называется диф-

ференциалом функции и обозначается dy. Дифференциал

независимой переменной х равен

ее

приращению, т.е. dx^tSx,

Итак, если функция у

f(x) имеет производную / \х) в

точке

то дифференциал функции равен произведению произ-

водной fXx) на дифференциал независимой переменной, т. е.

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

297

f\x)dx.

2°.

Правила дифференцирования:

d{Cu)

Cdu\ 2, d{u±v)

du±dv;

(1)

d(uv)

udv

vdu; 4. d

(и \_ vdu-udv

3°.

Геометрический смысл

оифференциала.

Дифференциал

функции геометрически определяется разностью ординат каса-

тельной к кривой при переходе от точки

абсциссой х^ к точке с

абсциссой

Ах

(рис. 1.1).

XQ Л^О+АС X

Рис. 7.7

4°.

Инвариантность формы дифференциала. Форма диф-

ференциала не зависит от того, является аргумент функции не-

зависимой переменной или функцией другого аргумента. Если

= /(л:),где x

(p{t),TO

dy=f:dx=f:(p:dt. (2)

5°.

Дифференциалом второго порядка функции у

f{x) в

некоторой точке называется дифференциал в этой точке от ее

первого дифференциала и обозначается

d^y

d(dy)

y''dx\

(3)

Аналогично определяются дифференциалы высших по-

рядков

298 Гпава 7

d'y

d(d'y)

/V;

d{d'-'y)

/''^dx\ (4)

6°.

Если функция сложная ;; = f(x), гдех = ф(0 , то диф-

ференциал второго порядка d^y

d(f^dx) находится по фор-

муле

d'y

f:dx'+f:dx,

(5)

где dx

x'dt.

Дифференциал третьего порядка будет

d'y

r\dx)\3fUxd'x

fci'x, (6)

т.

д. Здесь штрихами обозначено дифференцирование по х.

Для дифференцируемой функции

j;=:/(x)

из приближен-

ного равенства Ду - dy следует

f{x

Ax)=^f{x)+f{x)Ax. (7)

Эту формулу используют при приближенных вычислениях.

8°.

Абсолютная величина разности между истинным значе-

нием какой-либо величины а^ и ее приближенным значением а

называется абсолютной погрешностью и обозначается

\а^-а\.

Абсолютная величина отношения абсолютной погрешнос-

ти к истинному значению называется относительной погреш-

ностью и обозначается д

-.—г.

Относительная погрешность

обычно выражается в процентах 5

-.—г

100%.

К|

Если приращение функции заменить ее дифференциалом, то

получим приближенное значение прирапхения Ay-dy .В этом

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

299

случае абсолютная погрешность равна

= |Ay-t/v|, а относи-

тельная погрешность будет 5 =

4.1.

Найти дифференциалы функций: а) у

х^-х-\-у[х,

х^-\

Решение, а) Находим производную данной функции

у'

Ъх^-\

2\}х

(

Отсюда дифференциал равен dy = y'dx = Ъх -1 +

б) Находим производную

tgx

COS

X sin2x

Отсюда дифференциал

dy ах,

sin2jc

в) Находим производную

2л/х

шс

у =•

(.41)'

Отсюда дифференциал будет dy

•

(.41)

6х'

(.41)'

(ir.

г) Производная по t равна х' =

За

sin^

/ cos

t. Отсюда диффе-

ренциал dx

= За

sin^

^ cos

tdt.

4.2.

Найти дифференциалы указанных порядков от фун-

кции:

а) >; =

3^"^^^

dy?; б) р =

в)

д;

= (х^~х + 1)\ rfV? г) ^сУ^^уУ^=а'^\ d'yl

sin2^

, ^V?