Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.

300
гпава 7
Решение, а) Находим дифференциал 1-го порядка
1
dy^T'^'\^Z-
1
'ibtgj:
-т—<ir = 21n3 dx.
tgjc cos X
Дифференцируя еще
раз,
получим
rfV
= 21n3
sin2x
21n3-
72,._oi^'i sin2jc
-2-3^"^"COS2JC
-t&'
=
sin 2JC
^4j^3 3,„.,,ln3-cos2x^,
sin 2x
б)
Дифференцируя последовательно дважды, имеем
cos 2(р
(l -
<рМ+ф
sin 2^
dp^l ^7 b ^^•
J V = 2((-sin 2^
• 2 (l
-<p-)-cos 2^
• 2(p
+ sin 2^
+
2(j9cos2^ Vl -<p^) +
+2(cos
2^(1
- ^^) + ^ sin 2(jf))(l -
<p^)"
=
= 2(sin
2^(5^^
-\-2(p*) + 2(p cos
2^(1
- q)^))d(p^.
в)
Дифференцируя последовательно три раза, имеем
ф; = 3(л;^-x+l)^ (2x-l)d!x:,
rfV = з(2(х' -x
+
\){2x-lf+{x^ -x
+
lf 2]dx^ =
= 6(jc' -x+l)(5x^ -5x + 2)dx\
d'y = 6[{2x-l)(5x^ -5x+2)+(x^ -x+\){lOx-5))dx^ =
= 6{2x-l)(lQx^ -\Ox + l)dx\
r) Функция задана неявно. Находим первую производную
У =-
/д;УЗ
V'
, тогда dy = -
V^y
(ic.

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ ЗО^
Вычисляем вторую производную
у
ъ{х] х" ЪЧх''
отсюда а
y-—\\—jax
4.3.
Выразить дифференциал сложной функции через неза-
висимую переменную и ее дифференциал: а) y
=
yjx^
-Зх,
x
=
t^+l;6)
z
=
\ny, y
=
tgx, x
=
2t^+t;B) у
=
е\ x = tg^ пред-
ставить d^y через: l)xudx,2)tH dt.
Решение, a) Дифференциал сложной функции равен
, _ 2х-3 ,_
dy
=
y[x[dt.
Находим производные
Ух
- / ^ ? ^t -
^^-
Под-
lyjx -Ъх
ставляя значением в у[, окончательно получим
(2,'-1)«А
б)
Дифференциал сложной функции в этом случае имеет вид
dz
=
z\y\x\dt.
Находя производные Zy =—, у^— —,
jc'
= 4r +
l
ипод-
У COS X
ставляя их значения в выражение дифференциала, окончатель-
но получим
dz
=
г—(4/ + 1)Л =
)—^—^——.
j;cos'x'
sin (2(2/4/))
в) Находим дифференциал первого порядка
dy - y\dx = e^dx. Дифференциал второго порядка через xndx
равен d^y - y^dx^
=
e'^dx^.
Выразим теперь дифференциал через t и dt. Дифференциал
первого порядка будет dy =
y'^x'^dt
=
е""
— dt
=
е^^^
—.
cos / cos /

302 Гпава 7
Дифференцируя по
Г,
получим
е^^^
г—cos^^
+ e*^'2sin/cosr i . • о^
d'y^—^^ll dt'=e^^-^-^^dt\
COS t COS t
Если воспользоваться формулой (5), где // =
е"",
/^' =
е"",
(ix ^, то придем к такому же результату
cos t
cos t
2 r M \
dt
уCOS^
t J
cos t
4.4.
Вычислить приближенно: a) arctg
1,05;
6) lg9; в) 5^0,98.
Решение, a) Полагаем /(x) = arctgx, тогда /'(x) = ^.
Отсюда no формуле (7) имеем arctg (x -f Дх) = arctg x + ^ Ax.
Пусть
X
=
1,
тогда Дх = 0,05. Таким образом
arctg(l + 0,05) = arctgl + —^-0,05 = -
+
0,025.
б) Положим /(x) = lgx, тогда /'(х) = . Отсюда по
Ах
формуле (7) имеем Ig (х+Ах) = Ig х+ .
xlnlO
Пусть
X
=10, тогда
Ах
= -1 и Ig(l0~l) = lgl0+ "" .
^^ ^ ^ lOlnlO
Отсюда Ig9 =
1
- -^ = 0,956.
InlO
1 -— 1 1
в) Полагаем /(х) = л/х, тогда f'(x)
= —x
^
=—р=^.
^ ^ ^ ^ 5 5^7
Отсюда
л/х
+
Ах
=л/х+-

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ 303
Пусть
л:
=
1,
тогда Ах = 0,02 и ^1-0,02 =Vl+--;- или
5
Vi^
VW =1-0,004 = 0,996.
4.5.
Для функции
j;
=
х^
+ Зх
+1
найти приращение ордина-
ты касательной и приращение функции при переходе аргумента
X
от значения х-2 к
х-2,\.
Решение. Согласно геометрическому смыслу дифференци-
ала, приращению ординаты касательной соответствует диффе-
ренциал функции dy =
(2JC
+ Ъ)(Ь.
Прих = 2и tu:=Ax:=2,l-2=0,l получим ^=(2-2+3)0,1 = 0,7.
Приращение функции находим по формуле
АУ = /(Х +
АГ)~/(Х)
=
= (2,1'+3-2,1 + 1)-(2'+3-2 +
1)
= 11,71-11=0,71.
Следавательно, приращение ординаты касательной равно
0,7, а приращение функции 0,71. Так как Ау = ф'
+
аЛх, то
аАх =
0,71-0,7
= 0,01.
4.6.
Найти дифференциал
и
приращение функции у
=
х^
-Ix
при х
=
2 и
Ах
=
0,1.
Найти абсолютную и относительную по-
грешности при замене приращения функции её дифференциалом.
Решение. Имеем: dy =
{Ъх^
-2^dx,
Aj;=((x+A^f -2(x+At))-(jc^ ~2х)
=(3JC^
+3xAr+At' -2) Ar.
При x
=
2 и
Ax
= 0,l получим: ф = (3-2^-2)0,1 = 1;
Aj;
= (3-243'20,1 +
0,1'-2)0,1
= 1,061.
Абсолютная погрешность
А
= |Ау-ф'| =
0,061,
а относи-
тельная погрешность 5 = -,—г
100%
=
—
100% = 6% .
Н 1,061
4.7.
При измерении сторона куба х оказалась равной 4см,
причём максимально возможная при этом погрешность измере-

304 Г пава 7
ния Ах находится в пределах ±
0,01см.
Определить абсолют-
ную и
относительную погрешности при вычислении объёма куба.
Решение. Объём куба равен К =
х^
= 64 ст^. Возможная не-
точность измерения
|
Ах |=
0,01.
Отсюда абсолютная погрешность
IА FI«IJF1=
Ъугдх
=
3 •
4^
•
0,01
= 0,48. Относительная погреш-
ность
dV
V
^^100%
= 0,75%.
64
7.5. Приложения производной к задачам
геометрии и физики
1°.
Уравнение касательной и нормали к кривой. Значение
производной f\x)
в
некоторой точке х =
х^
геометрически пред-
ставляет угловой коэффииент касательной к графику функции
у
=
/(х) в точке
X
=
XQ
.
Из геометрического смысла производной следует, что уг-
ловой коэффициент касательной к кривой у = /(х) (рис. 7.8 ) в
точке M(Xo,jVo) М е у равен значению производной в этой точ-
ке,
т. е.
А:
= tga = /XXQ)
.
Поэтому, если в уравнение пучка пря-
мых, проходящих через точку М, подставить угловой
коэффициент касательной, то уравнение касательной к кривой в
данной точке примет вид
Нормалью к кривой в точке MixQ.y^) называется прямая,
проходящая через точку М перпендикулярно касательной к кри-
вой в этой
точке.
В
силу условия перпендикулярности двух пря-
мых
'~ к
, уравнение нормали имеет вид

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ
305
У-Уо'^'-
Пч)
(X-XQ),
если
Г{ХО)ФО,
Отрезки АМ
=
у^оХ^а,
BN^y^iga называются, соответ-
ственно, подкасательной и
поднормалью,
а длины отрезков AM
и ВМ—длинами касательной и нормали.
Рис. 7.8
2^.
Углом между кривыми y
=
f^{x) и
y-fii^)
^ точке их
пересечения М^{х^,Уо) называется угол между касательными к
этим кривым
в
точке М^. Этот угол находится по известной фор-
муле аналитической геометрии
tg9 =
/2Ч^о)^Д^о)
3°.
Отрезки, связанные
с
касательной и нормалью, в поляр-
ной системе координат. Пусть кривая задана в полярных коор-
динатах уравнением р
=
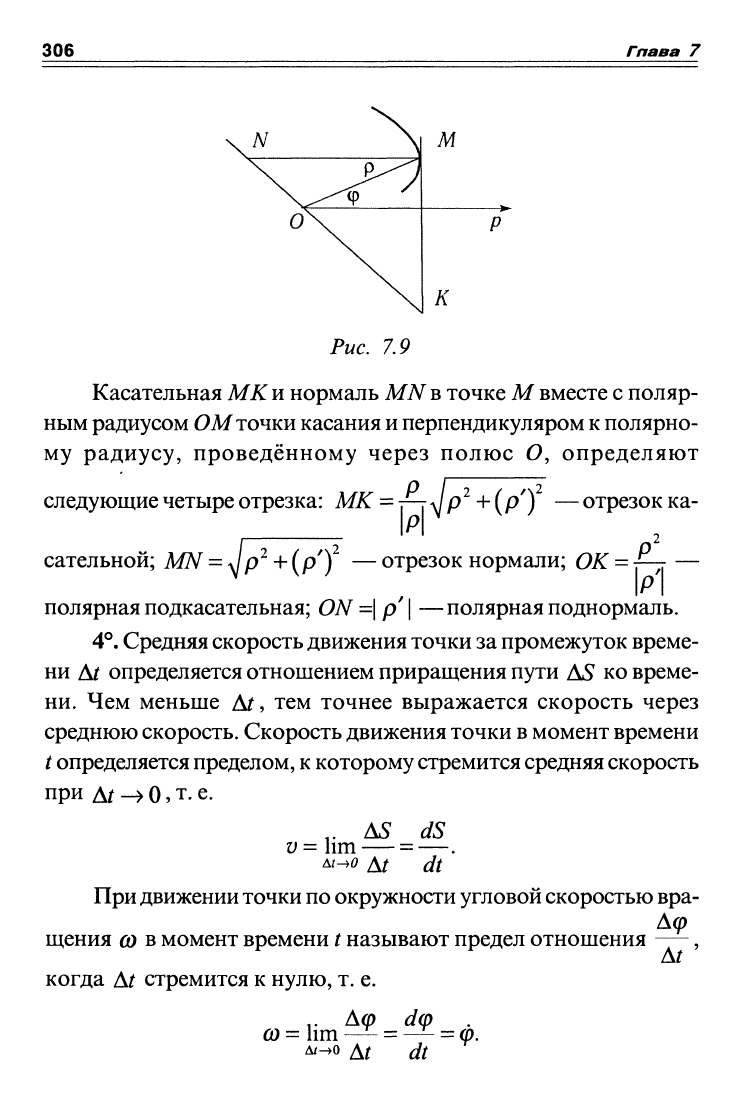
р{(р) (рис. 7.9), тогда угол,
образованный касательной МКи полярным радиусом р = ОМ,
определяется по формуле
tga = -^.
306
Гпава 7
Рис. 7,9
Касательная МК и нормаль MN
в
точке М вместе с поляр-
ным радиусом ОМ точки касания и перпендикуляром к полярно-
му радиусу, проведённому через полюс О, определяют
следующие четыре отрезка: МК = TIVP^+(P) — отрезок ка-
W
I
' ' 2
сательной; MN
=
Jp^+ {p'f — отрезок нормали; ОК
=
~-г —
\Р\
полярная подкасательная; ON
=\
р'\ —полярная поднормаль.
4°.
Средняя скорость движения точки за промежуток време-
ни At определяется отношением приращения пути AS ко време-
ни.
Чем меньше At, тем точнее выражается скорость через
среднюю скорость. Скорость движения точки в момент времени
t определяется пределом, к которому стремится средняя скорость
при Аг -> О, т. е.
,. AS dS
v= lim — = —.
^^^0
Д/ dt
При движении точки по окружности угловой скоростью вра-
А(р
щения
со
в момент времени t называют предел отношения —,
At
когда А^ стремится к нулю, т. е.
со
,. АФ dcp
lim -—^ = —^
Д^-^о At dt
•
ср.

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ 307
Таким образом, угловая скорость в данный момент равна
производной от угла поворота
(р
по времени.
Ускорение точки
w,
движущейся по прямой, есть первая про-
dv
изводная от скорости по времени
w
= — или вторая производ-
d'S *
пая от пути S по времени w = —^.
at
Угловое ускорение точки есть первая производная от утло-
го)
вой скорости
£ =
или вторая производная от угла поворота
,dt
d^cp
по времени
£
=—j-.
dt
Aq
5°.
Сила тока определяется как предел отношения — при
А/
—>
О, где Ад — положительный электрический заряд, пере-
носимый через сечение цепи за время At, т. е.
Д^^о д^ cit
Таким образом, сила тока
в
данный момент времени равна
производной от количества протёкшего электричества по вре-
мени.
6°.
Химическое истолкование производной. Пусть Q(t) -
концентрация вещества, получаемого в ходе химической реак-
ции в момент времени /. Тогда
C'[tQ)=
lim— — скорость
реакции в момент t^.
5.1.
Написать уравнение касательной и нормали к кривой
1 1
У-~—г вточке М(1,—).
ж^ XX , 2х
Решение. Находим производную у = ^ j и вычисля-
ем частное значение производной при х =
1:
уХ\) = —.

308
Гпава 7
Таким образом, уравнение касательной будет
Уравнение нормали к кривой в точке М(1,—) имеет вид
у--
=
1{х-\) или 4л:-2д;-3 = 0.
5.2.
Написать уравнение касательной и нормали к эллипсу
2 2 О
—+^^
=
1
вточке М(-,4).
9 25 5
Решение. Находим производную
2х 2уу' л / 25х
9 25 9у -
Вычисляем частное значение производной в точке М
/9Л 2591 5 ^
у — = = —
•
Отсюда уравнение касательной
1^5
j 9 54 4 ^^
у-4
=
--(х--) или
5jc +
4y-25 = 0.
4 5
Л
л 4Г 9^
'-4 = — X —
Н 5j
или
Уравнение нормали имеет вид у-
20JC-25>;
+ 64 = 0.
5.3.
На кривой у =
Зх^
- 4х
+1 найти
точку, в которой каса-
тельная параллельна прямой у
=
1х.
Решение. Пусть искомая точка касания есть
M(JCO,
j^^).
На-
ходим угловой коэффициент касательной в точке касания
к
=
у\х^)
=
6х^-4.
Поскольку касательная и прямая параллельны, то их угло-
вые коэффициенты равны
6JCQ
-4 = 2, откуда
Jc^
= 1.
Подставляя найденное значение абсциссы искомой точки в
уравнение кривой, находим её ординату
>^Q=31^-414-1
= 0.
Итак, точка М имеет координаты (1,0).

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ
309
5.4. Найти точку линии у
=
х^ -2х-^5,в которой касатель-
ная перпендикулярна прямой Зх +
6j^
-1 =
О,
составить уравне-
ние этой касательной. Сделать чертёж.
Решение. Пусть искомая точка есть М{х^,у^). Находим
угловой коэффициент касательной уХх^) =
2х^
-2. Угловой ко-
эффициент прямой
А:^
= —.
Из условия перпендикулярности прямых
/г^
=
,
где к^ —
угловой коэффициент касательной, находим абсциссу искомой
1 1
точки — =
—
2jCn~2
,
JCQ
= 2. Ординату точки М находим из
уравнения линии
у^=х1-
2х^
+
5
= 5. Уравнение касательной
будет j;~5 = 2(jc--2) или 2х-у
+ 1 =
0.
Чтобы построить график параболы, преобразуем её урав-
нение
j;
=
jc^
- 2х +
5
= (х
-1)^
+ 4, т. е. вершина параболы сдви-
нута на единицу вправо и на четыре единицы поднята вверх (рис.
7.10). Уравнения касательной и прямой, перпендикулярной ка-
сательной, показаны на рисунке.
1
\ ^
/
/
1 /2х-у=0
Зх+6у-1=д
X
Рис. 7.10
