Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

330

Гпава

Максимум и минимум функции называется экстремумом

функции. Значения аргумента, при которых функция имеет эк-

стремум, называются критическими значениями или критичес-

кими точками.

Чтобы найти экстремальные значения функции, надо найти

ее производную f\x) и, приравняв ее к нулю, решить уравне-

ние f\x)

О.

Корни этого уравнения, а также точки, производ-

ная в которых не существует, являются критическими точками,

т. е. значениями аргумента, при которых может быть экстремум.

Если знак производной при переходе через точку х^ меняет-

ся с плюса на

минус,

то

есть точка максимума; если знак про-

изводной меняется

минуса на

плюс,

то х^

есть

точка минимума;

если знак не меняется, то в точке

экстремума нет.

Иногда проще исследовать критическую точку по знаку

второй производной.

Если в критической точке, где первая производная равна

нулю,

/'XXQ)

ТО XQ есть точка минимума; если /'\х^)

О,

то

есть точка максимума; если

f'XxQ)

0, то такую точку

исследуют по первой производной.

2°.

Если функция задана неявно F(x,y)

0, то для того что-

, F^x.y) ^

бы у^= = 0, должно выполняться равенство

Fyi^.y)

F/(x,

>^)

О.

Здесь F^ и

F^,

производные от функции Fnoxuy,

найденные в предположении, чтоуихясзависят отхиу, соот-

ветственно. Решая совместно F{x,y)

0 я F^{x,у) =

О,

находим

критические точки. Экстремум функции в критических точках

находят по знаку второй производной у^ = у-. Если в кри-

тической точке J^!^ <

О,

то это точка максимума; если у^^>0 ,то

это точка минимума.

аИфФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

331

X X

9.1.

Исследовать на экстремум функции: а)

—

---2х\

6)у

х{х-2)\

Решение: а) Находим производную у -х^ -x-l- Прирав-

ниваем ее к нулю

jc^

- х -

О.

Корни этого уравнения

-1;

JC2

= 2 являются критическими точками.

Представим производную в следующем виде

У = (х +

1)(х

и рассмотрим методом интервалов, как меня-

ется знак при переходе через критические точки (рис. 7.22 ).

Рис. 7,22

При переходе через точку х, =-1 производная меняет знак

с плюса на минус, а при переходе через Хз = 2

минуса на плюс.

Значит, при Xj = -1 функция имеет максимум, а при

Х2

= 2 фун-

кция имеет минимум.

Находим экстремальные знчения функции: /(-1) =

максимум функции; /(2) = минимум функции. График

функции показан на

рис.

7.23.

Рис. 7.23

332 Гпава 7

б) Находим производную у

2(х -

2)^

(2х -1) и приравни-

ваем

ее

к нулю

(jc

2)^

(2х -1) = О. Корни этого уравнения

= 2,

JC2

—

являются критическими точками.

При переходе через точку

=2 производная знака не меня-

ет, поскольку данный множитель в квадрате, а при переходе че-

рез точку ^2 =

—

меняет знак с минуса на плюс. Значит, при

^2 =

—

функция имеет минимум.

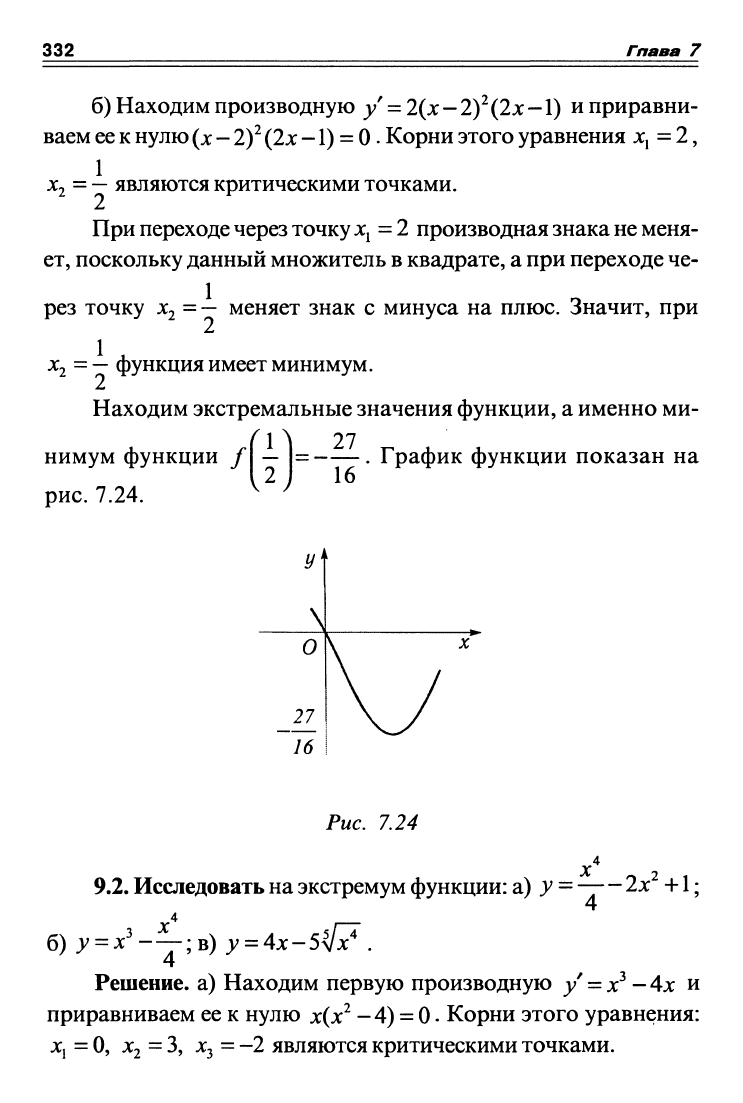
Находим экстремальные значения функции, а именно ми-

нимум функции /

рис.

7.24.

^1^

v2y

= . График функции показан на

Рис, 7,24

9.2.

Исследовать на экстремум функции: а) у

--— 2х +1;

6) у

х''

— ;в) у

4х-5^х' .

Решение, а) Находим первую производную

у^

х^

-4х и

приравниваем ее к нулю х(х^ -4) =

О.

Корни этого уравнения:

Xj =0,

Х2

Х3

= -2 являются критическими точками.

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ

333

Находим вторую производную у' =

Ъх^

-4 и выясним знак

второй производной в критических точках: ^^''(О) <

— функ-

ция имеет максимум; У\2) >

— функция имеет минимум;

у\-2)

> О

—функция имеет минимум. Определяем экстремаль-

ные значения функции: /(0) =

— максимум функции;

/(2) = -3 — минимум функции; /(-2) = -3 — минимум функ-

ции. График функции показан на рис. 7.25.

Рис. 7,25

б) Находим первую производную у

Зх^

jc^

и приравни-

ваем ее к нулю jc^(3-x) = 0. Корни этого уравнения:

Xj =

О,

^2 =

являются критическими точками.

Находим вторую производную У = 3х(2-х) и выясним

знак в критических точках.

При ^2 =

вторая производная у'ХЗ)

< О

—функция имеет

максимум. При Xj =0 вторая производная У(0) = 0, следова-

тельно, судить об экстремуме

нельзя.

Проверим наличие экстре-

мума по первой производной. Поскольку при переходе через

точку Ху=0 первая производная знака

не

меняет,

то

точке

экстремума нет.

Определяем в точке ^2 =

максимальное значение функ-

ции f(^) =

334

Гпава 7

График функции показан на

рис.

7.26.

Рис. 7.26

в) Функция определена на всей числовой

оси.

Находим про-

изводную у'

4-4 -j= = -j=rlyjx -1

Приравниваем производ-

л!

X yj X

ную

нулю (^/х -1) = о

находим критическую точку х^ =

При

переходе через точку jc, =

производная у' меняет знак с мину-

са на плюс, следовательно, в точке

функция имеет мини-

мум j;(l) = ~l.

Приравнивая к нулю знаменатель производной, получаем

\1х =0. Отсюда находим критическую точку функции

Х2

= О,

в которой производная не существует. Очевидно, что в точке

х-0

производная

j;'

О,

а в точке х +

производная

j;'

< 0. Сле-

довательно,

Х2

есть точка максимума функции у{0) =

(рис.

7.27).

9.3.

Найти экстремальные значения функций:

а) ху^-х^у

2а';б) хЧ/-4ху

/ 2

Решение, а) Функция задана

неявно.

Находим F^ =у —Ixy

и F/=2X>'-X^

ПИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ

335

Рис. 7.27

Производная j; =

тогда, когда F^ =

О,

т. е.

- 2ху = О.

Решая совместно систему

{

ху^ -х^у

2а^,

/-2ху

находим критическую точку х = а, у=^2а.

1у

Вычисляем вторую производную

у]^

2ху-х^

. В

критичес-

кой точке

У^ос^~

у'^>0,

если а >

О,

у'^<0,

если а<0.

За

Таким образом, функция

при а>

имеет минимум, а при а <0

имеет максимум.

б) Находим F^ =4х —4у, Fy =4у -4х и приравниваем к

нулю

F/=0,

х^-у

Из решения системы

[х'^+У-4ху = 0,

[х'-у

= 0

находим критические точки х

0, у

^1з,

л/Т1

336 Гпава 7

Вычисляем вторую производную у^ = —— и определяем

"^ у 'X

ее знак в критических точках. Поскольку при

= 0,j = 0 и

Fy =

О,

то в окрестности этой точки уравнение может опреде-

лять у как неоднозначную функцию от х, поэтому точку (0,0)

оставляем в стороне.

При

л/3

вторая производная у^ = ^=—j=

= <

О,

т. е. при

= л/З функция имеет максимум, равный

Утях

= ^^7 .

8/^ - 3^9 3^3^^

При

= -

л/3

вторая производная у^ = т=—^ = > О,

т. е. функция имеет минимум, равный у^^

=z-^jTJ.

7.10« Наибольшее и наименьшее

значение функции

Наибольшим значением функции у = /(х) на некотором

отрезке

[а,Ь]

называется самое большое, а наименьшим значе-

нием — самое меньшее из всех ее значений.

Если функция непрерывна в некотором интервале и имеет

только один экстремум и если это максимум (минимум), то он

будет наибольшим (наименьшим) значением функции в этом ин-

тервале (конечном или бесконечном).

При определении наибольшего и наименьшего значения

функции на отрезке

[а,Ь]

приравнивают первую производную к

нулю

j^'

и находят критические точки, лежащие внутри от-

резка

[а,Ь].

Далее вычисляют значения функции в этих точках и

на концах отрезка

[а,Ь],

т. е. находят f(a) и f{b). Из сравнения

значений функции в этих точках определяют наибольшее и наи-

меньшее значение функции.

аиффЕРШнииАпьноЕ

исчиспЕНИЕ функиии

337

10.1.

Найти наибольшее и наименьшее значение функции

7Г

на отрезке: а) У = -

j-,

[-2;2];б)

= x + cos2x,

[0;--];

в)

= хЧЗх'-9х +

20,

[-6,2].

Решение, а) Находим производную функции

У =•

+ х -2JC'

1-JC^

и приравниваем ее к нулю х -1 = 0.

хУ

Отсюда критические точки будут

х =

-1.

Поскольку кри-

тические точки лежат внутри интервала, то находим значения

функции в этих точках: у(1) =

—,

у{-1)

—

Вычисляем значе-

2 2

ния функции на концах отрезка [-2;

2]:

у(-2) = —, у(2) = —.

Теперь сравниваем значения функции в критических точках и в

точках на концах отрезка. Из сравнения видно, что наибльшее

значение функции будет у{^) ~ Т, а наименьшее yi^^) = ~"г. Гра-

фик функции на отрезке

[-2;2]

показан на рис. 7.28.

Рис. 7.28

б) Вычислим производную у'

\-2sm2x, приравняем ее к

нулю

2 sin

2JC

и находим критические точки, принадлежа-

ть

щие отрезку

[ 0; —

В данном случае имеем только одну критическую точку х =

12'

338

Гпава 7

Вычисляем значение функции в критической точке

на кон-

цах отрезка

71 л/з 6л/з +

тс

12 2

. Я0)

У\^

2я-3

Сравнение найденных значений функции показывает, что

наибольшее значение в точке экстремума у

тс+бл/з

, а

наименьшее на конце отрезка у

v3y

27С-3

График функции

7С

на отрезке [0;—] показан на

рис.

7.29.

01 iL

Pwc.

7.29

в) Вычисляем производную у

Зх^

6х

-9 и, приравнивая

ее к нулю, находим критические точки

jc^

+2х-3 =

0, jCj

=1,

Х2

=~3. Поскольку критические точки ле-

жат внутри отрезка [- 6,2], вычисляем значения функции в кри-

тических точках

у{1) =

\5, у(-3)

41. Находим значение

функции на концах отрезка ^^(-б) = -34, у(2)

22.

Сравнивая вычисленные значения функции

критическрос

точ-

ках и на границе отрезка, заключаем, что наибольшее значение

находится в критической точке

= -З и равно

>^(-3)

47,

а наи-

меньшее

фаничной точке

= -б

равно у{-6)

-34 (рис. 7.30).

аИФФЕРЕНиИАПЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

339

Рис. 7.30

10.2.

Найти наибольшее и наименьшее значения функций:

а) f(x)

e 2 ;б) (pix)

sm^x

cos^x;B) f(x)

^x^-l.

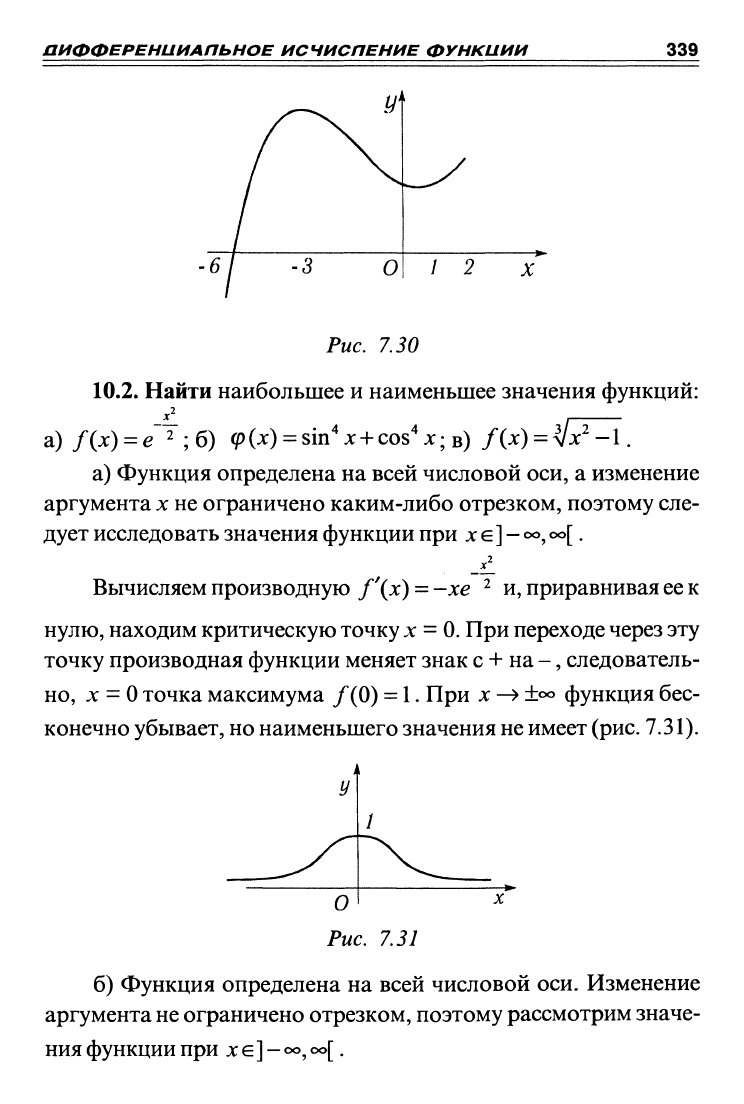
а) Функция определена на всей числовой оси, а изменение

аргумента х не ограничено каким-либо отрезком, поэтому сле-

дует исследовать значения функции при х е

]

©о,

оо[.

Вычисляем производную f\x) = -хе ^ и, приравнивая

ее

нулю,

находим критическую точку х

0. При переходе через эту

точку производная функции меняет знак с + на -, следователь-

но,

точка максимума /(0) =

При х^±^ функция бес-

конечно убывает, но наименьшего значения не имеет

(рис.

7.31).

б) Функция определена на всей числовой оси. Изменение

аргумента не ограничено отрезком, поэтому рассмотрим значе-

ния функции при

]

оо^

оо[