Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

360

Гпава 7

в) Функция определена на всей числовой оси х, бесконеч-

ных разрывов не имеет, поэтому не имеет и вертикальных асим-

птот.

Определяем наклонные асимптоты:

следовательно,

будет

ее

горизонтальной асимптотой.

Данная кривая бесчисленное множество раз пересекает свою

асимптоту J =

О,

переходя с одной ее стороны на другую в точ-

ках х

кп

(А:

= ±1,±2,...) и неограниченно приближаясь к ней

(рис.

7.49).

-2ж

Рис, 7.49

13.2.

Найти асимптоты кривых: а)/(д:) = в'';

Решение, а) Найдем горизонтальную асимптоту

lim/(jc) =

lime''

lim /(jc) = lim

e'^

JC-*oo JC->oo

следовательно, горизонтальная асимптота имеет вид у

Найдем теперь вертикальную асимптоту:

lim f{x) = lim

e""

oo,

lim /(JC) = lim

e""

=0,

jc->+0 x->+0 x-»-0 jr-»-0

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

361

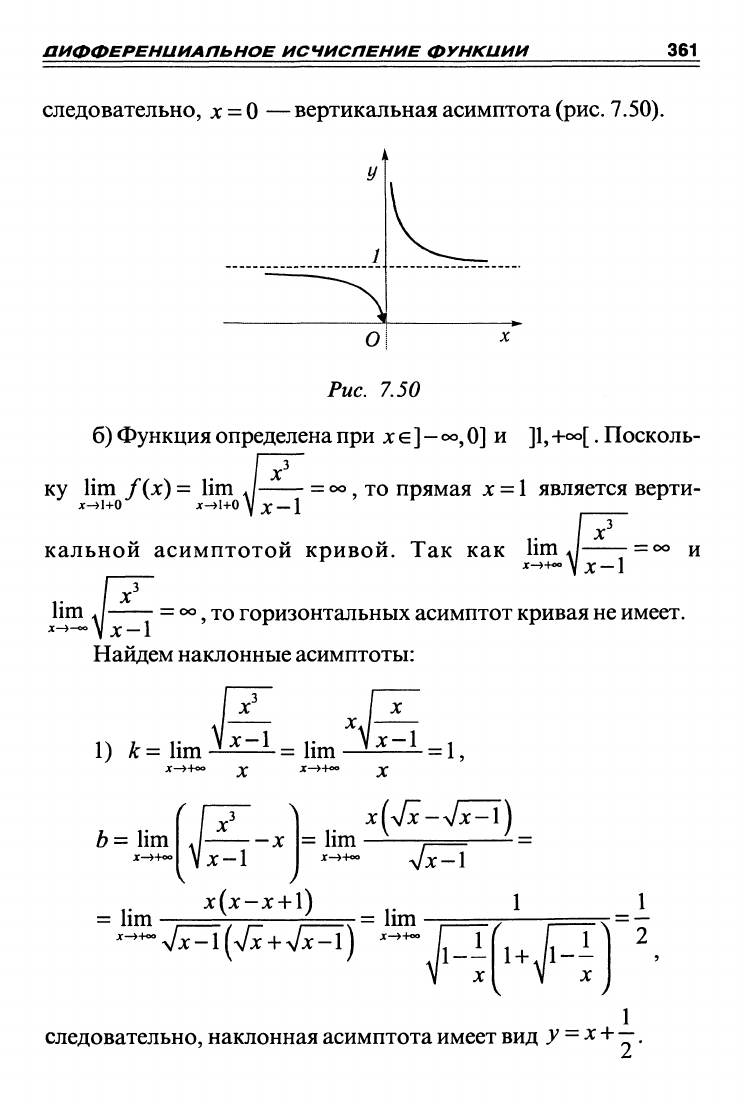
следовательно,

— вертикальная асимптота

(рис.

7.50).

0\ ^

Рис. 7,50

б) Функция определена при

]

оо^

]1,

+оо[.

Посколь-

ку lim f{x)

lim J =

©о ^

то прямая х =

является верти-

кальной асимптотой кривой. Так как lim

lim

^-^^

Jc-1

, то горизонтальных асимптот кривая не имеет.

х-1

Найдем наклонные асимптоты:

А:

= lim-^^^^= lim ^^ ^ =.1,

Ь= lim

П7~ Л x(yfx-yjx-l)

— X \=Ит ^ , ^:

jc(x-jc + l)

= lim / = Imi

ч/;с^(л/х

>/;Г^)

""'4

i+ji

__j_

"^"2

следовательно, наклонная асимптота имеет вид

У —

+ —

362

Гпава 7

2) к= lim

^х-1

b = lim

x-l

•

+ х

Сделаем замену: x

-t,

-> -оо, t -^оо, тогда:

= lim^^^^

-limj—=-lim 1-1-=

~1,

= lim

ч+\

= lim

—^ 7=^ ^

lini

—

^ ^ :

= -lim-

Г7

1+J1+

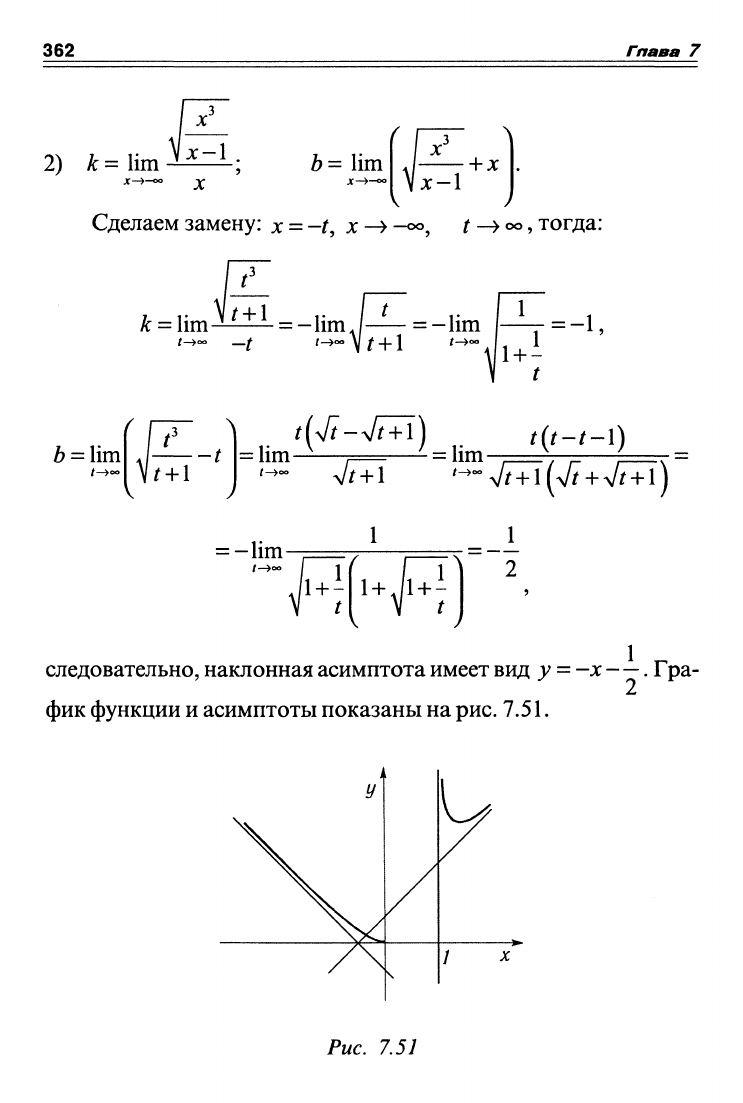
следовательно, наклонная асимптота имеет вид

у--х—.

Гра-

фик функции и асимптоты показаны на

рис.

7.51.

Рис. 7.51

аИФФЕРЕНиИАПЬНОВ ИСЧИСЛЕНИЕ ФУНКЦИИ

363

1 t

13.3.

Найти асимптоты кривых: а) х--^ у

—

—-;

б)-=ТГ7' ^=717' '^ ^

Решение, а) При /_^0л:—>оо; yz=. =

О,

следователь-

но,

кривая имеет горизонтальную асимптоту y

При t -^

-> 1;

-~>

«^,

следовательно, кривая имеет вертикальную асим-

птоту

б) При /

—> ±1

функция обращается

бесконечность. Ищем

уравнения наклонных асимптот:

h = lim

te'

J \

v'-'' '-'%

= lim

e4t-\)

= -lim-

'-^1 (l-/)(l + r) ^^4 + / 2'

Z?^

= lim

^ fe'

/^-1

v'-''

'-'%

= lim

.4^-fi)

e-' 1

^^-i(l-/)(l + r) 2 2^'

следовательно, наклонные асимптоты имеют вид 7-^^:7,

у^-хЛ-

2е

в) Приведем уравнение заданное в полярных координатах

к параметрическому виду: х =

asmcp

-, где (р —

(р

(Р

параметр. При ^-^0

х—>оо,у

= а,т. к. lim ^ = а . Сле-

довательно, кривая имеет горизонтальную асимптоту у

(рис.

7.52).

364

Гпава 7

Рис. 7.52

13.4.

Найти асимптоты кривых: а) у^=6х^+х'',

x'-i

Решение, а) Поскольку коэфициент при старшей степени у

(т. е. при у^) равен 1, то вертикальных асимптот нет. Для на-

хождения наклонных асимптот подставим в данное уравнение

Ах +

6, тогда получим

к'х^

-^Зк^Ь+ЗкхЬ^

+Ь'

-6х' -х'

О.

Приравнивая к нулю коэффициенты при старших степенях

X (т. е. при х^ и х^), получим систему

к'-1

\зк^Ь-6

Из

решения системы имеем /: =

Ь = 2 .

Таким

образом,

кри-

вая имеет одну наклонную асимптоту у

х-\-2.

б) Так как функция непрерывна на всей числовой оси, кро-

ме

точки

О,

то прямая х =

является вертикальной асимпто-

той

кривой.

Найдем наклонные асимптоты:

к = lim

Х->±оо

х^-1

= 0,

6= lim

b= lim

x'-l

-Ox

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ

365

Сделаем замену: х = -^, х -^ -оо, / -^

оо,

тогда

Umi^

-l.

t^oo _^

Если найти вторую производную Г\х) =

•

3JC'~2

(.^-1)

,к

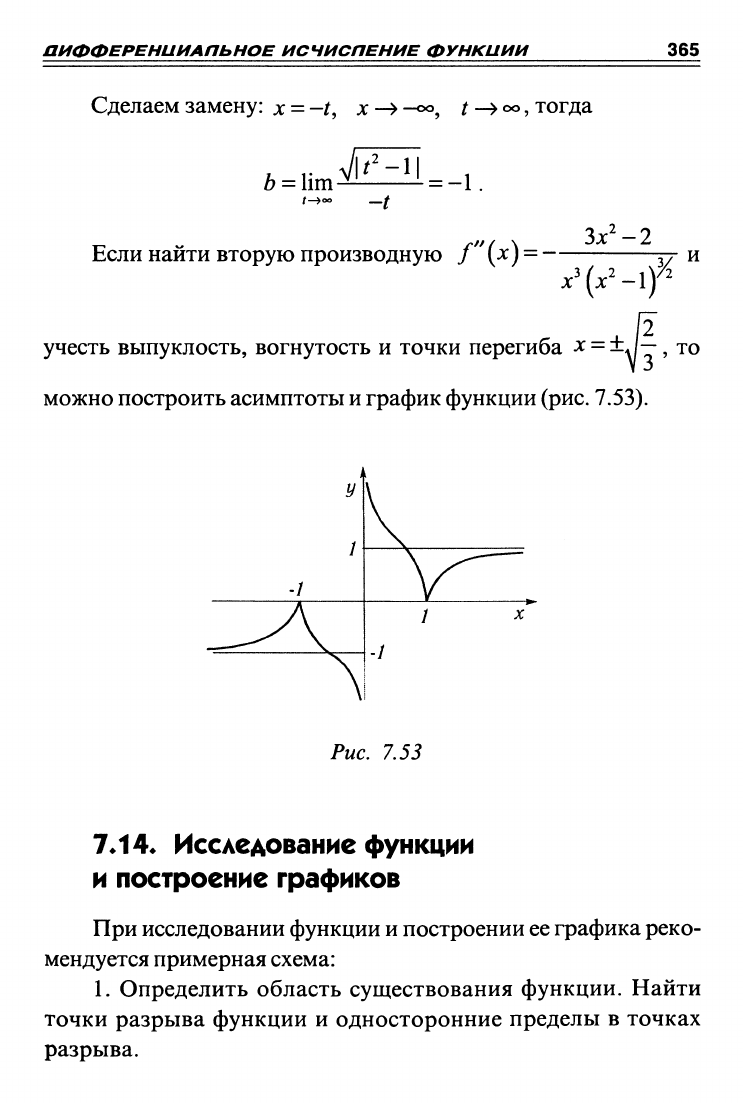
учесть выпуклость, вогнутость и точки перегиба ^ - -\/Т

'^^

можно построить асимптоты и график функции

(рис.

7.53).

Рис, 7.53

7.14. Исследование функции

и построение графиков

При исследовании функции и построении ее графика реко-

мендуется примерная схема:

Определить область существования функции. Найти

точки разрыва функции и односторонние пределы в точках

разрыва.

366 Гпава

Выяснить,

не

является ли функция периодической, четной

или нечетной, т. е. не симметричен ли график относительно оси

ординат или начала координат.

Найти точки пересечения графика функции

осями коор-

динат и интервалы знакопостоянства функции.

Найти точки экстремума

интервалы возрастания

убы-

вания функции. Определить значения функции в точках экстре-

мума, если такие существуют.

Найти точки перегиба и интервалы выпуклости и вогну-

тости графика

функции.

Определить значения функции

точках

перегиба.

6. Определить асимптоты функции.

Построить график функции, используя все полученные

данные.

По мере построения графика бывает очевидным, какие воп-

росы исследования целесообразно опустить, а какие добавить.

Если данных для построения недостаточно, то следует найти еще

несколько точек графика функции, исходя из ее уравнения. Ре-

зультаты исследования функции целесообразно заносить сразу

же на рисунок, тогда к концу проведения исследования график

будет практически построен.

14.1.

Исследовать функции и построить их графики:

х^

— 2

а) J^ =

JC'-8JC'"9;

б) у = - ^; в) у = \п -; г)

= jcV^

Д) у = г.

Решение, а) Областью существования функции является вся

числовая

ось.

Функция четная, следовательно, график функции

симметричен относительно оси ординат.

Полагая

л:

О,

находим точку пресечения графика с осью

ординат у

-9.

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКиИИ

367

Приведем функцию к виду у

{х^

1)(х^

-9), тогда, решая

уравнение

{х^

l)(jc^

-9) =

О,

точки пересечения

осью абсцисс

будут

db3.

Находим производную у -

Ах^

-16х и приравниваем ее к

нулю

4JC^

-1

6JC

ИЗ

решения уравнения х{х^ - 4) =

находим

критические

точки Xj

О,

^2 =

Хз=-

Находим вторую про-

изводную /' =

12х^

-16. Так как у\±2) > О, то точки Xj =

Хз

= -2 есть точки минимума функции, а так как у\0) <

О,

то

точка

есть точка максимума. Значения функции в экстре-

мальных точках равны:

j;(0)

-9;

j^(±2)

= -25.

Чтобы отыскать возможные точки перегиба, решаем урав-

нение: у'

= 0;

12х^ -16 = 0, откуда х =

±-7=-.

Так как /' ме-

л/З

няет свой знак при переходе через эти точки, то при этих

значениях х график функции имеет

перегиб.

Находим ординаты

точек перегиба: у

161

При неограниченном возрастании х

по

абсолютной величи-

не функция стремится к бесконечности lim

(х*

-Sx^ — 9) =

£»

График функции показан на

рис.

7.54.

Рис. 7.54

368 г пава 7

б) Функция существует всюду, кроме точек х = ±v3 . Пря-

мые

= V 3 и

= -л/3 являются вертикальными асимптотами

функции. Найдем односторонние пределы в точках разрыва

lim -^ =

оо;

lim

;с-^ч/з-оЗ-л:^ ' х^>/з+оЗ-х^

Х' v3

lim

г-

оо;

lim

^->-N/3-0

3-X^ '

;,_,_7з+0

3-Х^

функция нечетна, следовательно, ее график симметричен

относительно начала координат. При х =

имеем ;; =

О,

следо-

вательно, график функции проходит через начало координат.

^ , х^(3~х)(3 + х)

Находим производную ;; =

—^^

-^^—- и приравнива-

\р

—

Х)

ем ее к нулю х (3-х)(3 + х) = 0 . Корни этого уравнения

Рассмотрим методом интервалов изменение знака

j^'при

пе-

реходе через эти точки

(рис.

7.55 ). Следовательно,

точке х = -3

функция имеет минимум у(-3)=4,5, а в точке х =

имеет макси-

мум

j^(3)

= - 4,5. При переходе через х =

производная знака

не меняет, следовательно, в точке х =

экстремума нет.

-3 0 3

Рис. 7,55

Находим вторую производную у = —~——^. Вторая про-

6х(9 + х')

(3-х^)^

изводная у' -

при х =

и меняет знак с минуса на плюс при

переходе

через

эту

точку,

следовательно, и точка х =

О есть

точка

перегиба.

аИффЕРЕНиИАПЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

369

Находим асимптоты кривой:

= lim— ^ =

-1;

fe = lim

f x'

3-х'

•+x

lim-

•3-х'

= 0,

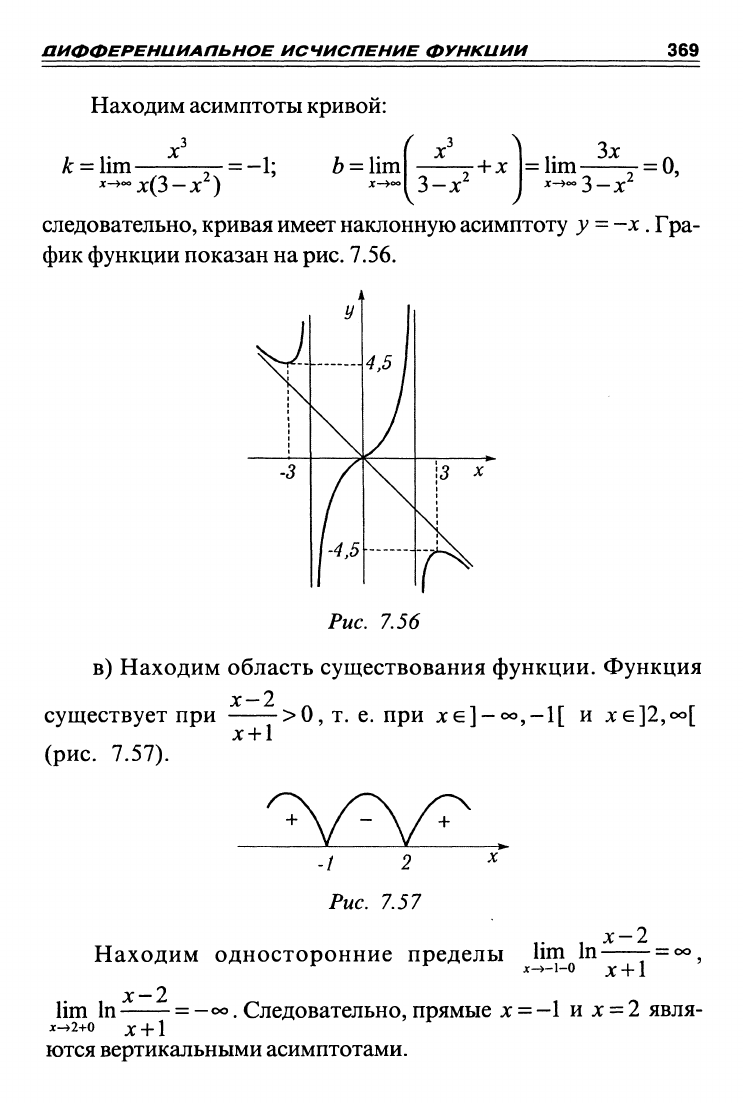
следовательно, кривая имеет наклонную асимптоту у

-х. Гра-

фик функции показан на

рис.

7.56.

Рис. 7.56

в) Находим область существования функции. Функция

существует при >0, т. е. при

JCG]--OO,-1[

XE]2,OO[

(рис.

7.57).

х +

-/ 2 ^

Рис. 7.57

Находим односторонние пределы пт ш

lim In

jc-2

= -с». Следовательно, прямые х = -1 и х = 2 явля-

х-42+0

+ 1

ются вертикальными асимптотами.