Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.

370
Гпава 7
Находим производную У = Производная не
(х + 1)(х~2)
обращается в нуль ни при каком значении х, значит экстрему-
мов нет.
и . „ 3(1-2х)
Найдем вторую производную у = ^^-2 —Т ^ прирав-
(х + 1)
(х~2)
няем
ее к
нулю
1 - 2х
=
О,
х
=
—, но точка х
= —
не входит в
об-
2 2
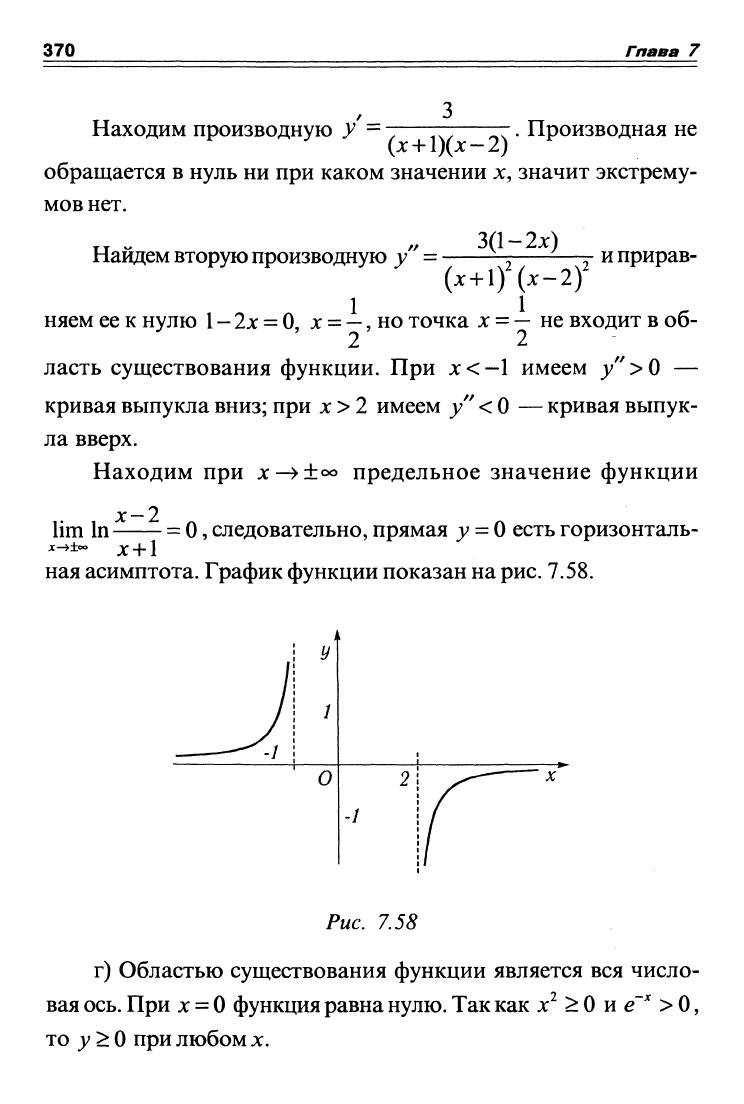
ласть существования функции. При х < -1 имеем /' >0 —
кривая выпукла вниз; при х > 2 имеем у" <0 — кривая выпук-
ла вверх.
Находим при X—>±оо предельное значение функции
х~2
lim In =
О,
следовательно, прямая
j;
=
О
есть горизонталь-
пая асимптота. График функции показан на
рис.
7.58.
О
'1
Рис. 7.58
г) Областью существования функции является вся число-
вая
ось.
При
X
=
О
функция равна
нулю.
Так как х^ >
О
и e""" > О,
то
3^
>
О
при любом
X.

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ 371
Находим производную у'
=
хе'""
(2
-
jc)
и приравниваем
ее
к
нулю
хе'""
(2 -
х)
= О.
Решая это уравнение, находим критические точки х^=0
и ^2 = 2. Поскольку производная меняет знак согласно схеме
(рис.
7.59), то в точке
jc
= 0 функция имеет максимум, рав-
4
ный нулю, а в точке х
=
2 минимум, равный у(2) - —,
0 2^
Рис. 7.59
Находим вторую производную у" = e'"" (2 - 4х
+ jc^)
и при-
равниваем ее к нулю в'"''(2-4х + х^) = 0, откуда jCj2 =2±v2 .
Поскольку вторая производная меняет знак согласно схеме
(рис.
7.60), то в точках jc,2 =2±v2 функция имеет перегиб и
при
X
<
2
-
л/2
кривая выпукла
вниз,
при х е
]2
- л/2,2 + л/2 [ кри-
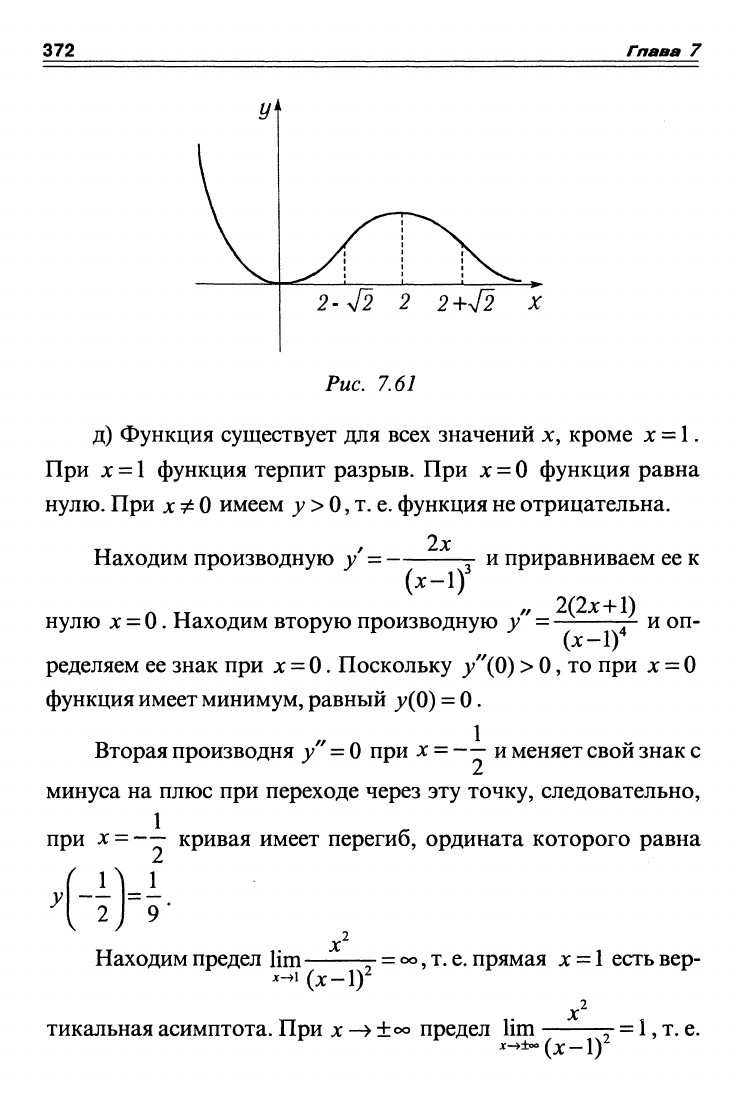
вая выпукла вверх, при хе]2 + л/2,оо[ кривая выпукла вниз.
2-42 2+42 ^
Рис. 7.60
Находим пределы:
х^
2х 2
lim х^е ""=«>, Итх^е
""
=lim — = lim — = lim—= 0,
Т.
е. прямая у
=
0 есть горизонтальная асимптота. График функ-
ции показан на
рис.
7.61.
372 Гпава 7
У\
2-42 2 2+42 X
Рис. 7.61
д) Функция существует для всех значений х, кроме х = 1.
При
X
=
1
функция терпит разрыв. При х =
О
функция равна
нулю.
При х^О имеем
j;
>
О,
т. е. функция не отрицательна.
Находим производную У = -
2х
(^-1)
и приравниваем ее к
л тт // 2(2х+1)
нулю
X
= о. Находим вторую производную у =
-т-
и оп-
(х-1)
ределяем ее знак при х =
О.
Поскольку у\0) > О, то при х =
О
функция имеет минимум, равный ;;(0) = О.
Вторая производня у"
= О
при х = — и меняет свой знак с
минуса на плюс при переходе через эту точку, следовательно,
при х = — кривая имеет перегиб, ордината которого равна
Находим предел lim
X
--1 (х-1)'
=
с»,
т. е. прямая х =
1
есть вер-
тикальная асимптота. При х
—>
±оо предел lim
X
^"^±-*(х-1)^
= 1, т. е.
аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ
373
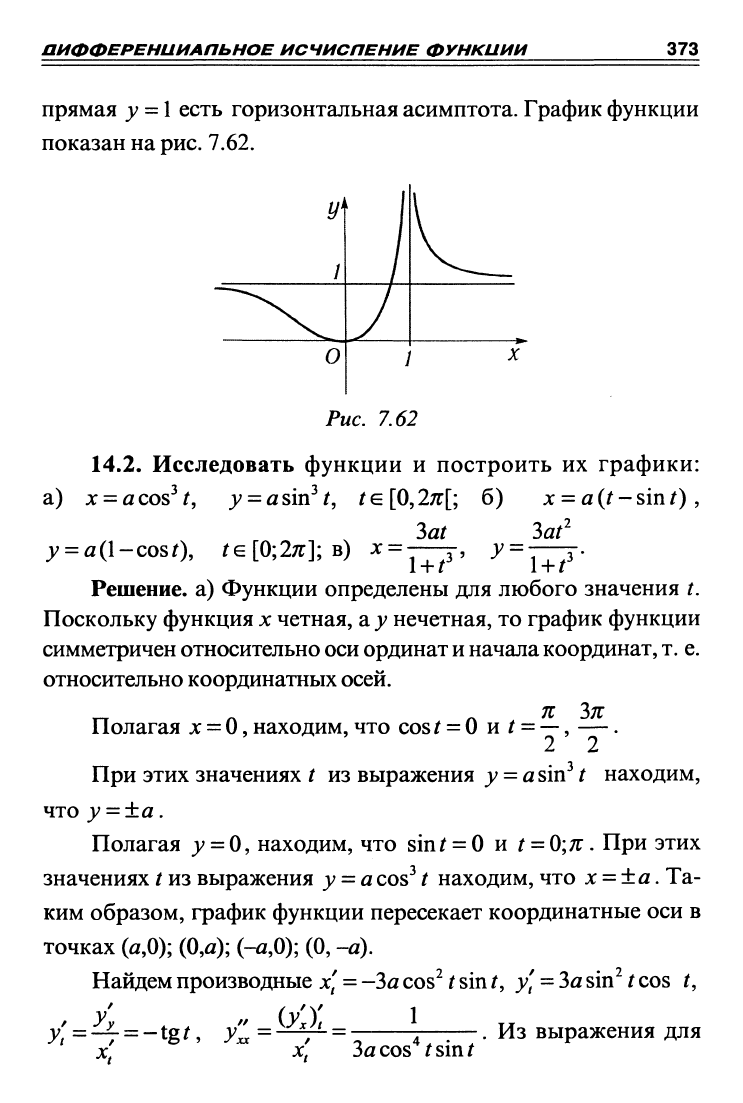
прямая у =
1
есть горизонтальная асимптота. График функции
показан на
рис.
7.62.
Рис. 7.62
14.2.
Исследовать функции и построить их графики:
а) x = acos^^ y
=
a^w^t,
ге[0,2л:[; б) x = a{t-smt) ,
Ъаг
ЗаГ
y
=
ail-costl te[0;2K];B) x
=
j—^,
^^l
+
t''
Решение, a) Функции определены для любого значения t.
Поскольку функция
X
четная, а у нечетная, то график функции
симметричен относительно оси ординат
и
начала координат,
т.
е.
относительно координатных осей.
Полагая
jc
=
О,
находим, что
cos ^
=
О
и t
= — ,
—.
При этих значениях / из выражения у = ^fsin^ t находим,
что у
=
±а.
Полагая у
=
0, находим, что sin/ =
О
и / = 0;л:. При этих
значениях / из выражения у
=
а
cos^
t находим, что х
=
±а. Та-
ким образом, график функции пересекает координатные оси в
точках ((2,0);
{0,а);
(-а,0);
(О,
-а).
Найдем производные
х'^
= -За
cos^
t sin
Г,
у' =
За
sin^
t cos /,
1
r X 3a
COS
tsmt
Из выражения для

374
Гпава 7
производной ;;' определяем критические
точки.
При
^
=
О,
Г=
л:
п Ъп
производная равна нулю, а при
^
= —,
^
= — не существует.
Таким образом, область изменения параметра / разбивается на
четыре интервала
п
2
к
7'"
И
,2л:
При ^6 0,-
производная
j;^
< О, а >^^ > О, т. е. функция
/
убывает и график функции направлен выпуклостью вниз. При
^Е
к
\п\
j^^
> о и
j;
аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ
375
Рис. 7.63
б) Функция определена при любом значении параметра t из
интервала
^
G
[0,2;г].
Найдем точки пересечения графика
с
осями
координат. При
jc
=
О,
sin
^
=/, / =
О.При;;
= 0, cos/ = l,/ = 0,
t
=
27t' Отсюда следует, что кривая при
^
=
О
проходит через на-
чало координат, а при t-ln пересекает ось Ох
в
точке х
=
2ка
•
Найдем производные х' = л(1-со8/), y[
=
as\nt,
sin
Г
„ cos/(l--cosO-sin^^ 1
л=-
Л
1-cos^'
"^
^
a(\-cost)^
a(l-cosO^
Приравнивая у[ к нулю,
из
уравнения sin
^
=
О
находим зна-
чения параметра
в
критических точках / =
{0;;г;
2;г}.
Первая про-
изводная не существует при l-cos^ = 0, т. е. при значениях
параметра
^
=
{0;
27г}.
При переходе параметра через критичес-
кие значения
Г
=
{0;2я},
т.е. в окрестности
(О
-е,
О
+ е),
(27Г
~е,
2л:
+ г), где |^| >
О,
производная у[ меняет
знак
с
минуса на
плюс.
Отсюда следует, что касательная к графи-
ку функции
в
точках х
=
{О;
2па\ параллельна оси Оу, При t
=
n
вторая производная у'^<0,т,с. точка x
= 7ia
точка максимума
функции у
=
2а. Более того, поскольку у'^ <0
нз,
всем интерва-
ле
^ G
[О;
2;г],
то кривая на этом интервале выпукла вверх.

376 Гпава 7
При изменении г от
О
до ;г производная у^ >
О,
следова-
тельно, кривая возрастает. При изменении t
от ж
ц,о2п произ-
водная у'^ <
О,
следовательно, кривая убывает. Все сказанное
позволяет представить график в виде (рис. 7.64). Полученная
кривая представляет траекторию точки круга радиуса а катя-
щегося без скольжения по прямой Ох за время одного оборота
круга
и
называется циклоидой.
Рис. 7.64
в) Функция определена при всех значениях г, кроме
Г
=
-1.
При / =
О
координаты х =
О,
j =
О
и при t ->±<^ координаты
X,
J -> О, т. е. начало координат служит особой точкой и в нем
кривая сама себя пересекает.
Найдем наклонную асимптоту. Угловой коэффициент равен
A:
= lim^=lim
^^-» x{t) ^-^-1
^3at'l + t'^
1
+ r 3at
Параметр
b = lim {y{t) - kx{t)) = lim
3at
'3at'
JC->-l
x-^-l
=-1.
3at
\+r \+r
= lim
= -a
^-'-n-t + r
Отсюда уравнение асимптоты x
+
y
+
a
=
0.
При изменении t от -сю до
-1,
точка {х,у) из начала ко-
ординат удаляется в бесконечность, причем значения х — по-
ложительны, з, у — отрицательны, т. е. ограничены

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ
377
асимптотой, расположенной в четвертом квадранте.
При изменении / от
-1
до
О
точка
{х,у)
из бесконечности воз-
вращается к началу координат, причем значения jc — отрица-
тельны,
г.
у — положительны, т. е. ограничены асимптотой,
расположенной во втором квадранте. При изменении / от
О
до
-оо точка описывает против часовой стрелки петлю, располо-
женную, судя по значениям х,у, в первом квадранте.
у
Обозначая
^
=
—,
нетрудно перейти к уравнению функции в
X
неявном виде F(jc, у)
=
х^
+у^
-- Заху = О .
Находим производные
/:
=
3{х'-ау),Г:
=
3(/-ах),
л=—
F:
X —ay
Прирав-
Fy у -ах
нивая у^=0 и решая это уравнение совместно с уравнением
F(x,y)
=
0, находим критические точки х
=
0, у
=
0 и
х = ал/2, у = ау/4- Вычислим у'^ при х = ау/2 по формуле
F'' 6х
У1Х
- —т = 2
•
Т^^ ^^^ ^ исследуемой точке >^^ < О,
Fy ХУ -ОХ)
то это точка максимума у^^
=
ал/4; х = ay/l.
В точке (0,0) F/ =
О
и F'
=
0, поэтому можно утверждать,
что касательными в этой точке служат оси координат. Учиты-
вая все
это,
представим график функции
(рис.
7.65). Полученная
кривая называется декартовым листом.
Рис. 7.65

378 Г пава 7
1Л
5.
Формула Тейлора
и
Маклорена
1°.
Если функция f{x) определена
и
дифференцируема п+1
раз в некоторой окрестности точки х^ = а , то она может быть
представлена в виде суммы многочлена
w-ой
степени и остаточ-
ного члена R^ (формула Тейлора)
/(х)=/(а)+^(х-й)+^(х-«)Ч ...
^i-^ix-aJ^K,
(1)
1!
2! п\
где R^^- ^-^ —; с = л
+
0(х~а); О<0<1 — оста-
(w
+
1)!
точный член в форме Лагранжа.
Формула Тейлора (п-го порядка) позволяет представить
функцию /(х) в виде многочлена «-ой степени и оценить с по-
мощью остаточного члена 7?„ возникающую при этом погреш-
ность, которая может быть сделана сколь угодно малой.
2°.
При а =
О
формула (1) принимает вид
/м=/(о)./М../^.ч
...
.!^.:к,
(2,
1!
2! п\
где
,
и называется формулой Макло-
рена. К этому частному случаю формулу Тейлора можно свести
с помощью перехода
к
новой независимой переменной ^ = х - л.
Остаточный член в формуле Тейлора иногда записывают в
форме Пеано R^ = (9((х - а)"), которая в ряде случаев бывает
более удобна (вычисление пределов). Остаточный член в форме
Пеано для формулы Маклорена имеет вид R^ = 0(х'').
15.1.
Для функций а)
е"
\
б) sinx; в) cosx; г)
(1
+ х)'";
д)
1п(1
+ х), написать формулу Маклорена л-го порядка и оце-
нить погрешность.

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ 379
Решение, а) Если /(jc) = e'', то и /^"^(jc) = e'' при любом
w=
1,2,3,
...
Так как /(0) = 1, и /^"^(0) = 1, то по формуле (2)
^-=1 + ^+^1+ ... + —+ Л„.
1!
2! п\ "
Точность разложения определяется остаточным членом
/^
^«"7
ТГч-^"
• Оценим погрешность. Так как
(« +
1)!
е"" 3
I
^«
1"^
/ . 14, ^"^^' 'г^' например, при х = 1,
|
/?„(1) |< —; при
(w
+
1)!
(/1
+
1)!
10
•2"'^*
X
= 2,
I i?„ (2)
|< и т. д. При любом значении х при «
—> ©о
(« +
1)!
остаточный член стремится к нулю и чем больше «, тем точнее
разложение. При
л:
=
1
можно получить формулу для приближен-
ного вычисления числа е
,111 1
е-1 +
—+
—+ —+ ... +
—
1!
2! 3! пУ
б) Пусть f{x) = sin
X,
тогда /(0) = О;
^-ь|\
Л0) = 1;
^ к
f\x)
= cosx = sin
f'\x)
= - sin
X
=
sin I
rV) = COSX = sinfx + 3|\ /'» = -l;
Х +
2^|,Г(0) = 0;
/''^=sin
Разложение примет вид
x-\-n—
,
/<">(0)
= sin«|.
