Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

390 Гпава 8

1.3. Найти область определения функций:

а) z = ln(x4/-l);6) ^== / =г\'&) z = arcsin-;

X у X

г) 1=^^х-\-у

,]х-у;д) 2

\пху;ё) /(р,(р)

рфт(р.

Решение, а) Функция определена, если х^ +у^ -1>0 или

х^

+у^ >l,T.Q, областью существования данной функции явля-

ется часть плоскости вне единичного круга с центром в начале

координат.

б) Функция

принимает вещественные значения при усло-

2 2 2 2

ВИИ 1 >0 ИЛИ —

—

<1,

Т. е. областью существова-

4 3 4 3

ния функции является открытый эллипс. Граница эллипса не

входит в область существования функции.

в) Функция определена, если х^О и -1< —<1 или

-JC< у<х. Областью существования функции является часть

плоскости, заключенная между двумя биссектрисами y

—

x^^

у = -X

содержащая ось Ох, за исключением начала координат

0(0,0).

г) Функция определена, если

x-fj;>0

и х-^-О^^. г. об-

ластью существования функции является внутренняя час ь пра-

вого вертикального

угла,

образованного биссектрисами, включая

сами биссектрисы.

д) Функция определена, если

х>^

> О, т. е. областью суще-

ствования функции является часть плоскости, лежащая внутри

первого и третьего координатных углов, исключая границы.

е) Функция принимает вещественные значения при условии

sin

(р

> О, т. е.

л:,

р — любое. Областью определения

будет верхняя полуплоскость.

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИЙ 391^

1.4. Найти область определения функций:

в) и = arcsin

—

Решение, а) Функция зависит от трех переменных и прини-

мает вещественные значения при z

—

-у^ > О, или 2>х^ л-у^,

т. е. областью существования функции

является часть простран-

ства, заключенная внутри параболоида, исключая сам парабо-

лоид.

б) Функция зависит от трех переменных и принимает

2 2 2

вещественные значения при 1 т~

7-О? или

а Ъ с

-у+-^+ -:;-< 1, Т. е. областью существования функции и

а b с^

является часть пространства, заключенная внутри трехосно-

го эллипсоида, включая границу.

в) Функция зависит от трех переменных и определена, если

л/л:"

+ у"

с' + у'

z^O и -1<-^^^

=—<1,или

0<jc^+/<z^

1.5. Найти линии и поверхности уровня функций:

а) 2 =

д:^-У;б)

w=x^+/+z^

Решение, а) Уравнение линий уровня имеет вид

х^ -

j;^

= С, т. е. линии уровня равносторонние гиперболы. При

С >

вершины гиперболы расположены на оси Ох, при С <

—

на оси Оу,

б) Уравнение поверхностей уровня имеет вид

х^ +

j;^

= С, т. е. поверхности уровня — это семейство сфе-

рических поверхностей

центром в начале координат.

392 Гпава

8.2. Предел функции нескольких

переменных. Непрерывность

1°.

Число

называется пределом функции

/(М) при

^MQ,

если

для

любого числа

г >

всегда найдется такое

число

5 >

О,

что для

любых точек

М,

отличных

от М^ и

удов-

летворяющих условию

IММ^

, будет иметь место неравен-

ство \f{M)-A\<e.

Предел обозначают

Цщ f{M) =

У4

. В

случае функции двух

переменных Ит/(jc,у)^А^

X-^XQ

2°.

Теоремы

о пределах. Если функции

f^{M) и /зСМ) при

стремятся каждая

конечному пределу,

то

а)

Jim

(у;(М) + /з(М))

= Jim

У;(М) +

Jim

/,(М);

б)

Jim

(у;(М)/,(М))

Jim y;(M)Jim /,(М);

в)

lim

^^-^^^—- =

^ ; lim

fJM)^0.

M-.M,

f (M) lim

/2 (M)

м-^л/о

-^ 2 ^

3°.

функция

/(М)

называется непрерывной

точке

М^,

если она удовлетворяет следующим трем условиям:

а) функция

f{M)

определена

точке

М^;

б) существует предел

lim f(M);

в) lim/(M)

/(Mo).

Если

точке

М^

нарушено хотя

бы

одно

из

этих условий,

то функция

этой точке терпит разрыв. Точки разрыва могут

образовывать линии разрыва, поверхности разрыва и

т.

д. Фун-

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИЙ 393

КЦИЯ f{M) называется непрерывной в области G, если она не-

прерывна в каждой точке этой области.

Из определения непрерывности функции в точке следует,

что бесконечно малым приращениям аргументов соответствует

бесконечно малое приращение функции.

^. Jjcy + l-l

2.1.

Найти пределы функций: а) lim-

^-^0 х + у

б) lim^HW; в) limV^; г) lim(l + ;c4;;^)"^^V .

Решение, а) Преобразуем предел следующим образом

кх'

Пусть у

кх, тогда lim . = О.

"-^4(l + A:)(Vfcc'+l+l)

б) Воспользуемся первым замечательным пределом

sina sin

,. sinxv ^ , ^

lim =

Тогда hm ^ = limx :i-=:21 = 2.

Пусть

fcc,

т. e. рассмотрим изменение

л:

и j вдоль пря-

мой. Тогда

',::;^'+/

;^^4i+t^) i+*'

Таким образом, предел имеет различные значения

зависи-

мости от выбранного к, т. е. функция не имеет предела.

г) Воспользуемся вторым замечательным пределом

lim(l+B)P =в. Тогда

394 Гпава 8

lim(l +

jc^

+ yM ^'V =lim

(H-x4/)^'-^x = e-'=i

2.2.

Найти точки разрыва функций: а) 2 =

1п(л:^

Ч-^'^);

б)"

= -т—^—Г-

Решение, а) Функция z = 1п(х^ + }^^) терпит разрыв в точке

О,

= О.

Следовательно, точка 0(0,0) является точкой разрыва.

б) Функция не определена

точках, в которых знаменатель

обращается в нуль, т. е. х^ +

j;^

О.

Следовательно, поверх-

ность конуса у^ л-у^ - z^ является поверхностью разрыва.

8.3. Частные производные первого порядка

1°.

Пусть

(XQ,

j^Q)

— некоторая произвольная фиксирован-

ная точка из области определения функции z =

z(x,

у). Прида-

вая переменной х приращение Ах, находим приращение функции

z-z{x^y) в точке

(^o^J^o)

^^ переменной jc:

Az =

z(Xo

Ax,

>^o)

Z(XQ

J/Q

Предел отношения lim — называ-

ется частной

производной

1-го порядка от функции z по пере-

менной X в точке (Хо,>^о) и обозначается ~- или

zj^x^y).

ох

Аналогично определяется и обозначается частная производная

от

Z по

>^:

— =

(х,

у^. Производная от функции z =

z(x,

у) по х

находится,

предположении, что j остается постоянной, по обьи-

ным правилам и формулам дифференцирования. Если функция

зависит от нескольких переменных z = z(x,,X2,...,х^) , то част-

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИЙ

395

пая производная

—

находится в предположении, что все пере-

Ъх.

менные (кроме

jc^)

постоянные величины.

2°.

Функция

(Xj,

^2,...,

jc^)

называется однородной фун-

кцией степени

т,

если

для

некоторого действительного числа

справедливо выражение

z(Ax,,Ax2,

... ,AxJ =

A'"z(xj,X2,

... ,xj.

Теорема Эйлера. Если однородная степени

функция

Z (jCp

JC2,...,

JC^)

имеет частные производные по каждой из пе-

ременных X.,

то

справедливо равенство

mz{x,,x^,

... ,xJ =

XiZ;(Xj,jC2.-.-^J +

' -^2^X2

V"^l 9 "^2 ' • • • 9 -^И

/'"•••"'

-^n

^JC„

V-^1 ? -^2 9 • • • 9 -^/1 / •

3.1.

Найти частные производные:

a) z= ^ .;

-^y

z =

xysin(2x +

3>^);

в) z =

^cos(2x-j;)

; r) z = 2

д)

z =

;е)2

^^'-^ж)

z =

arctg

—

Решение, a) Полагая

постоянной величиной, находим про-

изводную по х:

у(х^+у^)-ху2х

_ у(у^ -х^)

Эх~ (Х^+УУ ""(ХЧ/)'-

Полагая

постоянной

величиной,

находим производную

по>^:

_ х(х^

+у^)-ху2у

_ х(х^ -у^)

д^~ {x'+/f "(хЧ/)^-

б) Полагая

постоянной величиной, находим

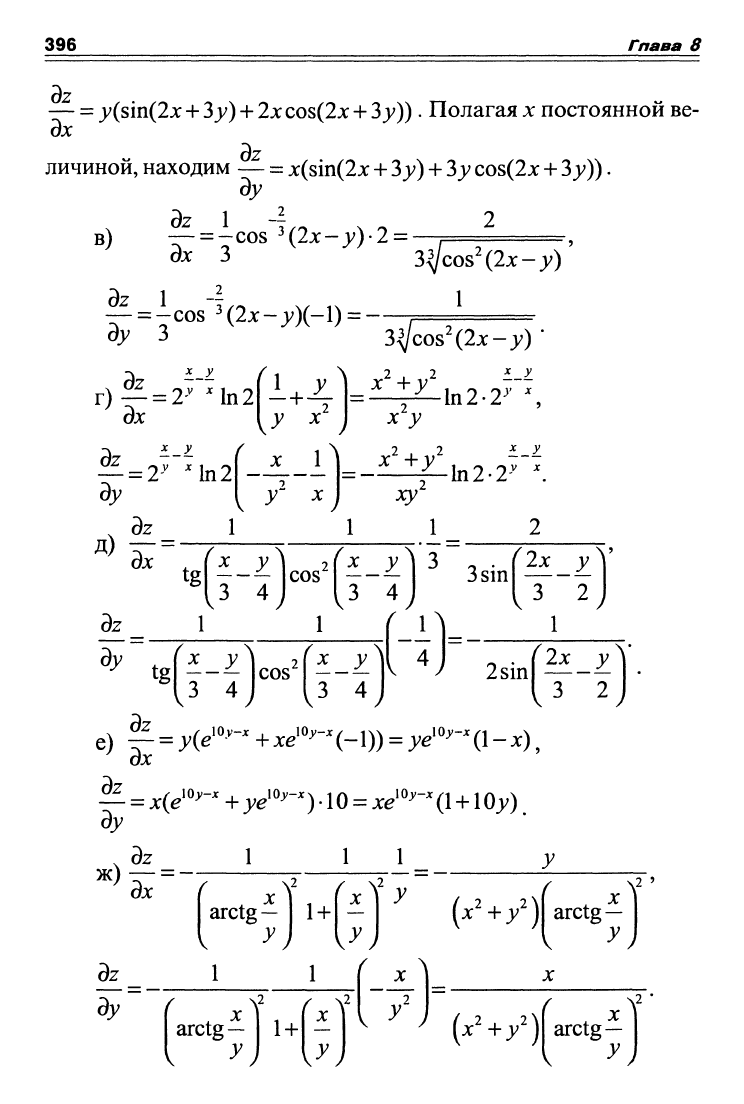
396 Гпава 8

Ъх

>'(sin(2j£:

3;;) + 2xcos(2x

Зу)). Полагая х постоянной ве-

личиной, находим — = x(sin(2x +

3;^)

3;^

cos(2x + Зу)).

ду

dz 1 -f 2

в) — = -cos ^(2x-j;)-2 =

^х 3 3^cos'(2x->;)

^ = -cos'^(2x-;;)(-l) = , ^

Эу 3 3^cos'(2x-j) •

г)—=

Мп2

Эх

dz ---

— =

"Ы!

ду

^41

[у X )

у-

х)

х'у

хЧ/

X у

\n2-V

X у

1П2-2-''

ху

Д)

1 1

Кг")

3z_

1 1

X у\3 ~ .

cos —— 3sin

3 4

3 2

Г n

£_Z

3 4

cos

^-Ziv V

3 4

2 sin

2x у

e) ^ =

;^(e'"^-^

xe'"^-^

(-1)) = У^-^

- X),

— =

xie""'-"

ye'''-")

10 =

xe'"'-"

+1 Oy)

ду

ж)

Эг

Эх

1 1 1

arctg-

Эг

Э;;

/ V

v^y

(хЧ/)

arctg-

/'„Л'

\yj

arctg-

V У)

(хЧ/)

arctg—

2 •

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИЙ 397

2 У

3.2.

Найти частные производные: а) и=хЗу +—;

б) I/ =

yJt-X^'-y^-Z^

Решение, а) Полагая у, z постоянными величинами, нахо-

ДИМ

производную по

х:

—•

3х у ,

ох

Полагая х, z постоянными величинами, находим

Эу

Z *

ди _ у

dz Z

Полагая

J постоянными, имеем ^ ^

^tl

1 , ^ ч

б) -г =12 2

2^"^^)

= -

OJC 2^Jt-x^-y^-z^

:(-2>') = -

ди 1

(-2z) =

^/^

л/^

•х^-/-

:?'

Г7'

Эг 2ф-х'-у'-2'

ф-x'-y^-z''

ди _ 1

3.3.

Найти: а) //(1;2),/,'(1;2), если /(х,у)

х^у-ху^ +\;

б)«:(1;0;2), ы;(1;0;2), м:(1;0;2),если

= ln(x'+/+z').

Решение, а) Находим частные производные

вычисляем их

значения в точке

(1 ;2)

3х'у-у\ /;

х'-3ху\ /;(1;2) = -2, /'(1;2) =

-11.

б) Находим частные производные и вычисляем их значения

вточке(1;0;2)

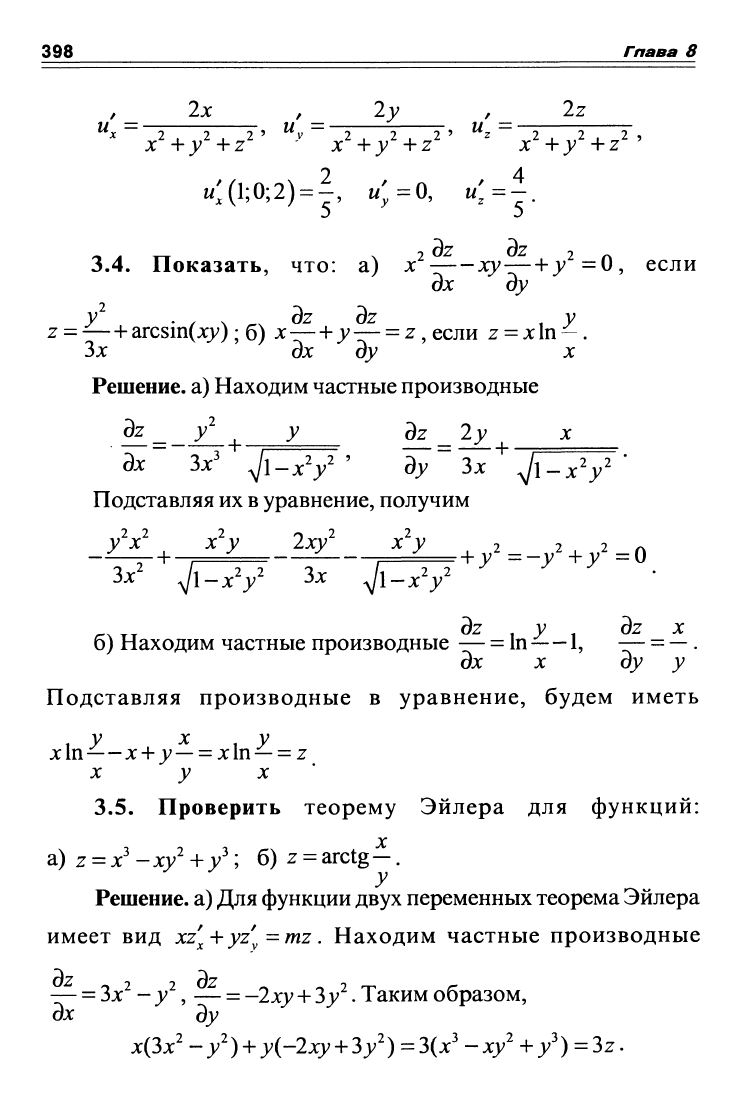
398 Гпава 8

, _ 2х , _ 2у , _ 2z

"^-777^'

"^"x4/+z^' ""^"ТТТ^'

3.4.

Показать, что: а) х -—ху—--^у =0, если

Эх оу

у , . . ^^ dz dz , V

— + arcsin(xy); б) X-—+

>^т—-

= ^,если z = jcln —.

Зх дх ду X

Решение, а) Находим частные производные

У , у dz __ 2£

Подставляя их в уравнение, получим

ух X у 2ху X у 2 2 2л

о) Находим частные производные — =

1п

-—

= —.

Эх X оу у

Подставляя производные в уравнение, будем иметь

У ^ л У

хт-—x +

j^—=

х1п —=

X ух'

3.5.

Проверить теорему Эйлера для функций:

а)

х^

-xv' + у^; б)

= arctg-.

Решение, а) Для функции двух переменных теорема Эйлера

имеет вид xz[^-yz'^=mz. Находим частные производные

— = Зх' -у^, — = -2ху +

Ъу^.

Таким образом,

Эх ду

х(3х' -/) + Я-2ху + 3/) =3(х' -х/ +/) =3z.

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИЙ 399

б) Находим частные производные —= ,

дх

X Л-у

X ^ ^У r^

тг =

—J 7

•

Таким образом,

—;

—; -

о, поскольку

ду

X Л-у JC +/ X +/

заданная функция однородная степени

= 0.

8.4. Дифференциал

функции и

его

применение к приближенным вычислениям

1^.

Пусть изменение функции z = /(х, у^ вызвано измене-

нием только одной переменной, например, х. Тогда приращение

A^z = /(jc

Ax,j^)-/(jc,j^) называется частным приращением

функции по

Частным диференциалом

функции z по х называ-

ется главная часть частного приращения, линейная относитель-

но приращения Ах

Частный дифференциал от функции z по х

равен произведению частной производной по х на дифференци-

ал независимой переменной, т. е.

dz ,

d.z = -dx. (1)

Аналогично,

d.^

Yy^y-

(2)

Если функция многих переменных

= /(хрХ^, ... ,х„), то

частные дифференциалы будут

d,u = ~^ dx,, d u =

^-dx^,

..., d u = ^-dx^ (3)

dXj 0X2 ox^

2°.

Если независимые переменные получают приращения

Ах,

Ау, то полное приращение функции z = /(х, у) определяет-

ся выражением