Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 111

measuring variability and spread

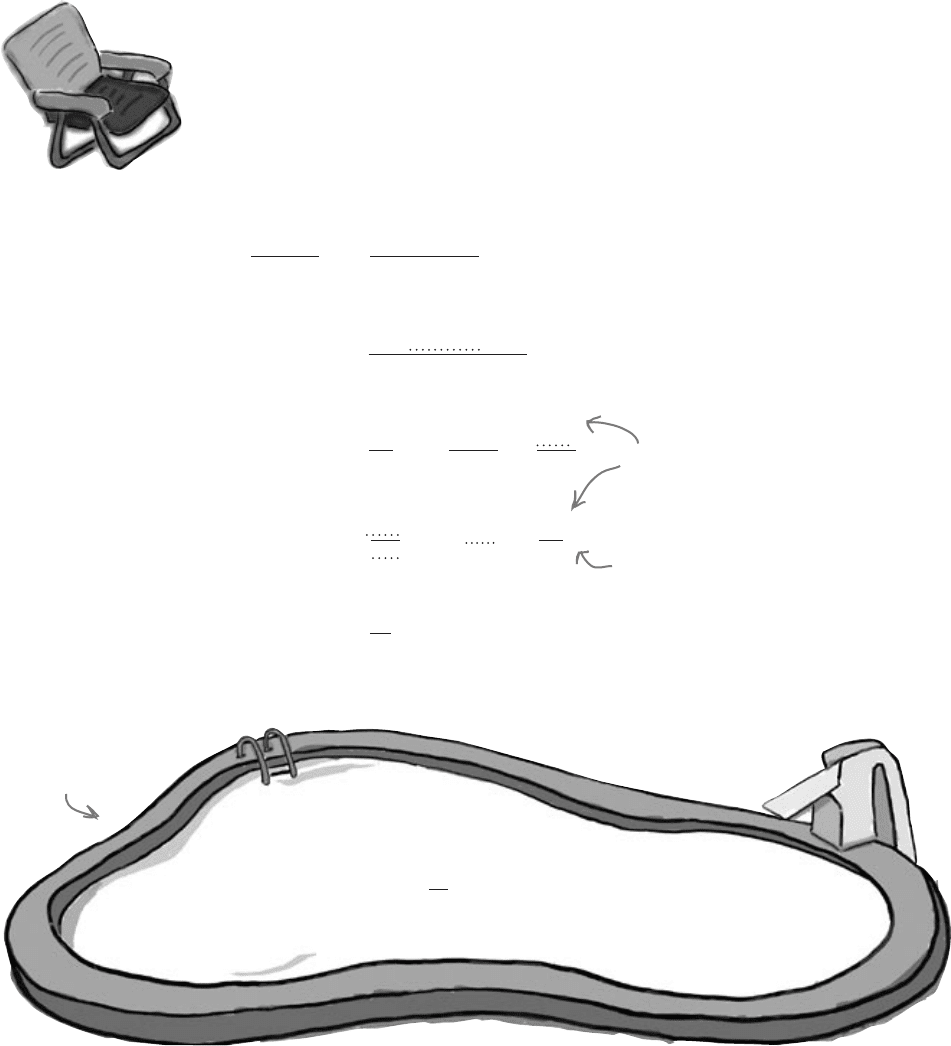
Pool Puzzle

There’s an easier calculation for calculating the

variance, but what is it? Your job is to take

equation snippets from the pool, and

place them into the blank lines in the

derivation. Each snippet will be used

only once, but you won’t need to use

every one. Your goal is to get to the

equation at the end.

Note: each snippet

from the pool can only

be used once!

- 2μx

+ 2μx

Σμ

See if you can

get from here...

to here.

Σμ

Psst - here’s a hint.

Remember that

Σx

μ.

Σ(x - μ)

Σ(x - μ) (x - μ)

Σ(x

+ μ

)

Σx

- μ

2μ Σx

Σx

nμ

- 2μ

Σx

112 Chapter 3

You didn’t need

these snippets.

+ 2μx

μΣμ

Σ(x - μ)

Σ(x - μ) (x - μ)

Σ(x

+ μ

)

Σx

- μ

2μ Σx

Σx

Σμ

nμ

- 2μ

There are n

of these.

The n’s here cancel

each other out.

Pool Puzzle Solution

There’s an easier calculation for calculating the

variance, but what is it? Your job is to take

equation snippets from the pool, and

place them into the blank lines in the

derivation. Each snippet will be used

only once, but you won’t need to use

every one. Your goal is to get to the

equation at the end.

pool puzzle solution

Σx

- 2μx

you are here 4 113

measuring variability and spread

A quicker calculation for variance

As you’ve seen, the standard deviation is a good way of measuring

spread, but the necessary variance calculation quickly becomes

complicated. The difficulty lies in having to calculate (x - μ)

for

every value of x. The more values you’re dealing with, the easier it

is to make a mistake—particularly if μ is a long decimal number.

Here’s a quicker way to calculate the variance:

The advantage of this method is that you don’t have to calculate

(x - μ)

. Which means that, in practice, it’s less tricky to deal with,

and there’s less of a chance you’ll make mistake.

So which form of the variance

equation should I use?

A: If you’re performing calculations, it’s

generally easier to use the second form,

which is:

This is particularly important if you have a

mean with lots of decimals.

How do I work out the standard

deviation with this form of the variance

equation?

A: Exactly the same way as before. Taking

the square root of the variance gives you the

standard deviation.

What if I’m told what the standard

deviation is, can I find the variance?

A: Yes, you can. The standard deviation

is the square root of the variance, which

means that the variance is the square of the

standard deviation. To find the variance from

the standard deviation, square the value of

the standard deviation.

I find the standard deviation really

confusing. What is it again?

A: The standard deviation is a way of

measuring spread. It describes how far typical

values are from the mean.

If the standard deviation is high, this means

that values are typically a long way from the

mean. If the standard deviation is low, values

tend to be close to the mean.

Can the standard deviation ever be 0?

A: Yes, it can. The standard deviation is

0 if all of the values are the same. In other

words, if each value is a distance of 0 away

from the mean, the standard deviation will

be 0.

What units is standard deviation

measured in?

A: It’s measured in the same units as

your data. If your measurements are in

centimeters, and the standard deviation

is 1, this means that values are typically 1

centimeter away from the mean.

I’m sure I’ve seen formulas for

variance where you divide by (n - 1)

instead of n. Is that wrong?

A: It’s not wrong, but that form of the

variance is really used when you’re dealing

with samples. We’ll show you more about this

when we talk about sampling later in the book.

Variance =

Variance

Here’s the quicker way of

calculating the variance

Vital StatisticsVital Statistics

114 Chapter 3

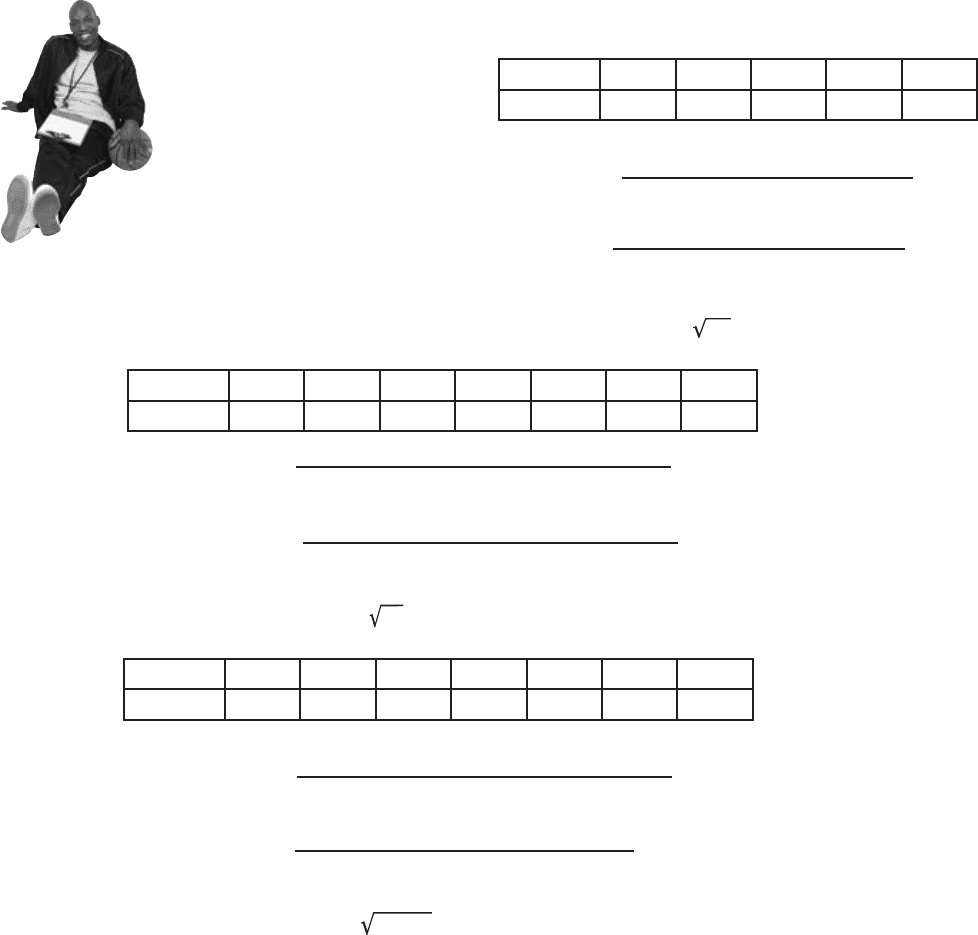
Score 7 9 10 11 13

Frequency 1 2 4 2 1

Player 1

BE the coach

Here are the scores for the

three players. The mean for

each of them is 10. Your job

is to play like you’re the

coach, and work out the

standard deviation for each

player. Which player is the

most reliable one for your team?

Score 7 8 9 10 11 12 13

Frequency 1 1 2 2 2 1 1

Player 3

Player 2

Score 3 6 7 10 11 13 30

Frequency 2 1 2 3 1 1 1

be the coach

you are here 4 115

measuring variability and spread

The generous CEO of Starbuzz Coffee wants to give all his employees a pay raise. He’s not sure

whether to give everyone a straight $2,000 raise or increase salaries by 10%.

a) What happens to the standard deviation if everyone at Starbuzz is given a $2,000 pay raise?

b) What happens to the standard deviation if everyone at Starbuzz is given a 10% pay raise instead?

116 Chapter 3

Score 7 8 9 10 11 12 13

Frequency 1 1 2 2 2 1 1

Player 3

Player 2

Variance = 7

+ 2(9

) + 4(10

) + 2(11

) + 13

= 49 + 162 + 400 + 242 + 169

= 2.2

Standard Deviation = 2.2 = 1.48

Player 1 and Player 2 both have small standard deviations, so the values are

clustered around the mean. But Player 3 has a standard deviation of 7.02,

meaning scores are typically 7.02 points away from the mean. So Player 1 is the

most reliable, and Player 3 is the least.

BE the coach Solution

Here are the scores for the

three players. The mean for

each of them is 10. Your job

is to play like you’re the

coach, and work out the

standard deviation for each

player. Which player is the

most reliable one for your team?

Score 3 6 7 10 11 13 30

Frequency 2 1 2 3 1 1 1

Score 7 9 10 11 13

Frequency 1 2 4 2 1

Player 1

be the coach solution

-100

Variance = 7

+ 8

+ 2(9

) + 2(10

) + 2(11

)

+ 12

+ 13

= 49 + 64 + 162 + 200 + 242 + 144 + 169

= 3

Standard Deviation = 3 = 1.73

-100

Variance = 2(3

) + 6

+ 2(7

) + 3(10

) + 11

+ 13

+ 30

= 18 + 36 + 98 + 300 + 121 + 169 + 900

= 49.27

Standard Deviation = 49.27 = 7.02

-100

you are here 4 117

measuring variability and spread

The generous CEO of Starbuzz Coffee wants to give all his employees a pay raise. He’s not sure

whether to give everyone a straight $2,000 raise or increase salaries by 10%.

a) What happens to the standard deviation if everyone at Starbuzz is given a $2,000 pay raise?

b) What happens to the standard deviation if everyone at Starbuzz is given a 10% pay raise instead?

The standard deviation is multiplied by 110%, or 1.1. The figures are stretched,

so the standard deviation increases.

standard deviation = ((1.1x) - (1.1μ))

= 1.1

(x - μ)

= 1.1 (x - μ)

= 1.1 times original standard deviation

The standard deviation stays exactly the same. The figures are, in effect, picked up

and moved sideways, so the standard deviation doesn’t change.

standard deviation = ((x + 2000) - (μ + 2000))

= (x + 2000 - μ -2000)

= (x - μ)

= original standard deviation

118 Chapter 3

That’s easy—Player 1

does best. Player 1 scores 75%

of the time, and Player 2 only

scores 55% of the time.

What if we need a baseline for comparison?

We’ve seen how the standard deviation can be used to measure how variable a

set of values are, and we’ve used it to pick out the most reliable player for the

Statsville All Stars. The standard deviation has other uses, too.

Imagine a situation in which you have two basketball players of different ability.

The first player gets the ball into the net an average of 70% of the time, and he

has a standard deviation of 20%. The second player has a mean of 40% and a

standard deviation of 10%.

In a particular practice session, Player 1 gets the ball into the net 75% of the

time, and Player 2 makes a basket 55% of the time. Which player does best

against their personal track record?

Just looking at the percentages doesn’t give

the full picture.

75% sounds like a high percentage, but we’re not taking into account the

mean and standard deviation of each player. Each player has scored more

than their personal mean, but which has fared better against their personal

track record? How can we compare the two players?

The two players have different

means and standard deviations,

so how can we compare their

personal performance?

Does this sort of situation sound impossible? Don’t worry, we can achieve

this with the standard score, or z-score.

Player 1

Player 2

μ = 70

μ = 40

σ = 20 σ = 10

Percentage Percentage

standard scores

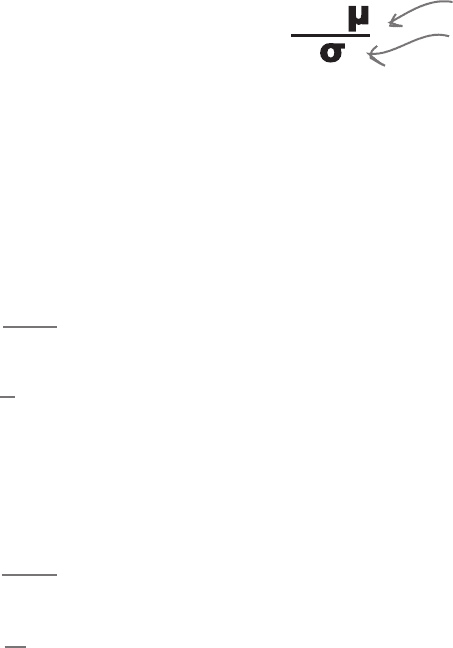
you are here 4 119

measuring variability and spread

Standard scores give you a way of comparing values across different sets of data

where the mean and standard deviation differ. They’re a way of comparing

related data values in different circumstances. As an example, you can use

standard scores to compare each player’s performance relative to his personal

track record—a bit like a personal trainer would.

You find the standard score of a particular value using the mean and standard

deviation of the entire data set. The standard score is normally denoted by the

letter z, and to find the standard score of a particular value x, you use the formula:

Calculating standard scores

Let’s start by calculating z

, the standard score of Player 1.

= 75 - 70

= 5

= 0.25

So using the mean and standard deviation to standardize the score,

Player 1 gets 0.25. What about the score for Player 2?

= 55 - 40

= 15

= 1.5

This gives us a standard score of 1.5 for Player 2, compared with a

standard score of 0.25 for Player 1. But what does this actually mean?

These are the mean and

standard deviation of the

set of data containing the

value x.

Let’s calculate the standard scores for each player, and see what those

scores tell us.

Use standard scores to compare values across data sets

x -

120 Chapter 3

Interpreting standard scores

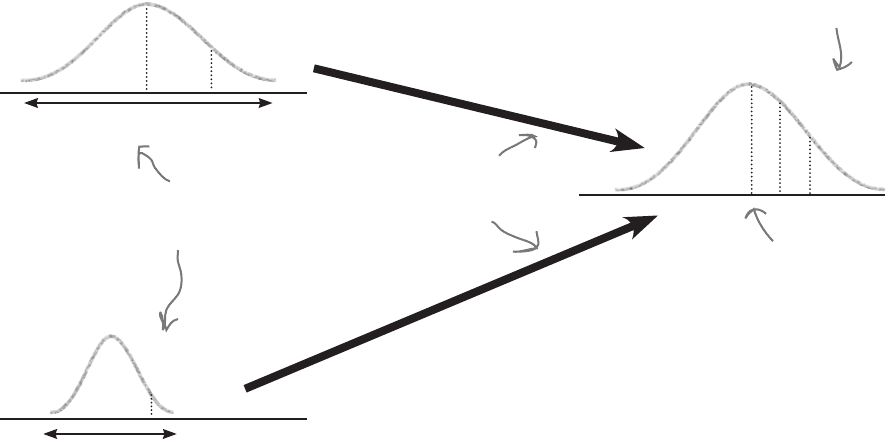
Standard scores give us a way of comparing values across different data sets even when the

sets of data have different means and standard deviations. They’re a way of comparing

values as if they came from the same set of data or distribution.

So what does this mean for our basketball players?

Each player’s shooting success rate has a different mean and standard deviation, which

makes it difficult to compare how the players are performing relative to their own track

record. We can see that in a particular practice, one player got the ball in the net more

times than the other. We also notice that both players are scoring at a higher rate than their

average. The difficulty lies in comparing performances relative to the personal track record

of each player.

The standard score makes such comparisons possible by transforming each set of data into

a more generic distribution. We can find the standard score of each player at the practice

session, and then transform and compare them.

So what does this tell us about the players?

The standard score for Player 1 is 0.25, while the standard

score for Player 2 is 1.5. In other words, when we

standardize the scores, the score for Player 2 is higher.

This means that even though Player 1 is generally a better

shooter and put balls into the net at a higher rate than

Player 2, Player 2 performed better relative to his own track

record. Player 2 performed better…for him.

interpreting standard scores

Player 1

Player 2

μ = 70

μ = 40

σ = 20

σ = 10

It’s difficult to

compare these two

data sets directly.

But we can

compare them with

z-scores.

= 0.25

= 1.5

Super-generic data

distribution Z

These are the

standard scores

for the two

players.