Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 321

geometric, binomial, and poisson distributions

2. On average, 1 bus stops at a certain point every 15 minutes. What’s the probability that no buses will turn up in

a single 15 minute interval?

3. 20% of cereal packets contain a free toy. What’s the probability you’ll need to open fewer than 4 cereal packets

before finding your first toy?

322 Chapter 7

Here are some scenarios. Your job is to say which distribution each of them follows, say what

the expectation and variance are, and find any required probabilities.

1. A man is bowling. The probability of him knocking all the pins over is 0.3. If he has 10 shots, what’s the probability he’ll

knock all the pins down less than three times?

If X is the number of times the man knocks all the pins over, then X ~ B(10, 0.3)

E(X) = np

= 10 x 0.3

= 3

For a general probability, P(X = r) =

x p

x q

n-r

P(X = 0) =

x 0.3

x 0.7

= 1 x 1 x 0.028

= 0.028

P(X = 1) =

x 0.3

x 0.7

= 10 x 0.3 x 0.04035

= 0.121

P(X = 2) =

x 0.3

x 0.7

= 45 x 0.09 x 0.0576

= 0.233

P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)

= 0.028 + 0.121 + 0.233

= 0.382

Var(X) = npq

= 10 x 0.3 x 0.7

= 2.1

long exercise solution

you are here 4 323

geometric, binomial, and poisson distributions

2. On average, 1 bus stops at a certain point every 15 minutes. What’s the probability that no buses will turn up in

a single 15 minute interval?

3. 20% of cereal packets contain a free toy. What’s the probability you’ll need to open fewer than 4 cereal packets

before finding your first toy?

If X is the number of buses that stop in a 15 minute interval, then X ~ Po(1)

E(X) =

= 1

For a general probability, P(X = r) = e

P(X = 0) = e

-1

x 1

= e

-1

x 1

= 0.368

If X is the number of cereal packets that need to be opened in order to find your first toy, then X ~ Geo(0.2)

E(X) = 1/p

= 1/0.2

= 5

For a general probability, P(X ≤ r) = 1 - q

P(X ≤ 3) = 1 - q

= 1 - 0.8

= 1 - 0.512

= 0.488

Var(X) =

= 1

Var(X) = q/p

= 0.8/0.2

= 0.8/0.04

= 20

324 Chapter 7

The geometric distribution

applies when you run a series of

independent trials, there can be

either a success or failure for each

trial, the probability of success is

the same for each trial, and the

main thing you’re interested in

is how many trials are needed in

order to get your first success.

If the conditions are met for the

geometric distribution, X is the

number of trials needed to get the

first successful outcome, and p is

the probability of success in a trial,

then

X ~ Geo(p)

The following probabilities apply if

X ~ Geo(p):

P(X = r) = pq

r - 1

P(X > r) = q

P(X ≤ r) = 1 - q

If X ~ Geo(p) then

E(X) = 1/p

Var(X) = q/p



The binomial distribution applies

when you run a series of finite

independent trials, there can be

either a success or failure for each

trial, the probability of success is

the same for each trial, and the

main thing you’re interested in is

the number of successes in the n

independent trials.

If the conditions are met for the

binomial distribution, X is the

number of successful outcomes

out of n trials, and p is the

probability of success in a trial,

then

X ~ B(n, p)

If X ~ B(n, p), you can calculate

probabilities using

P(X = r) =

n - r

where

= n!

r! (n - r)!

If X ~ B(n, p), then

E(X) = np

Var(X) = npq



The Poisson distribution applies

when individual events occur at

random and independently in a

given interval, you know the mean

number of occurrences in the

interval or the rate of occurrences

and this is finite, and you want to

know the number of occurrences in

a given interval.

If the conditions are met for

the Poisson distribution, X is

the number of occurrences in a

particular interval, and λ is the rate

of occurrences, then

X ~ Po(λ)

If X ~ Po(λ) then

P(X = r) = e

-λ

E(X) = λ

Var(X) = λ

If X ~ Po(λ

), Y ~ Po(λ

) and X and

Y are independent,

X + Y ~ Po(λ

+ λ

)

If X ~ B(n, p) where n is large and

p is small, you can approximate it

with X ~ Po(np).



bullet points

this is a new chapter 325

using the normal distribution

Being Normal

Discrete probability distributions can’t handle every situation.

So far we’ve looked at probability distributions where we’ve been able to specify exact

values, but this isn’t the case for every set of data. Some types of data just don’t fit the

probability distributions we’ve encountered so far. In this chapter, we’ll take a look at

how continuous probability distributions work, and introduce you to one of the most

important probability distributions in town—the normal distribution.

Discrete probability distributions can’t handle every situation.

So far we’ve looked at probability distributions where we’ve been able to specify exact

values, but this isn’t the case for every set of data. Some types of data just don’t fit the

probability distributions we’ve encountered so far. In this chapter, we’ll take a look at

how continuous probability distributions work, and introduce you to one of the most

important probability distributions in town—the normal distribution.

Whoever told you that’s

normal was kidding.

326 Chapter 8

Discrete data takes exact values…

So far we’ve looked at probability distributions where the data is

discrete. By this we mean the data is composed of distinct numeric

values, and we’re been able to calculate the probability of each of

these values. As an example, when we looked at the probability

distribution for the winnings on a slot machine, the possible amounts

we could win on each game were very precise. We knew exactly what

amounts of money we could win, and we knew we’d win one of them.

Discrete data

can only take

exact values

If data is discrete, it’s numeric and can take only exact values. It’s

often data that can be counted in some way, such as the number of

gumballs in a gumball machine, the number of questions answered

correctly in a game show, or the number of breakdowns in a particular

period.

You can think of discrete data

as being like a series of stepping

stones. You can step from value

to value, and there are definite

breaks between each value.

1 2 3 4 5

discrete data vs. continuous data

you are here 4 327

using the normal distribution

But why should I care

about continuous data?

…but not all numeric data is discrete

It’s not always possible to say what all the values should be in a set of

data. Sometimes data covers a range, where any value within that range

is possible. As an example, suppose you were asked to accurately measure

pieces of string that are between 10 inches and 11 inches long. You could

have measurements of 10 inches, 10.1 inches, 10.01 inches, and so on, as the

length could be anything within that range.

Numeric data like this is called continuous. It’s frequently data that is

measured in some way rather than counted, and a lot depends on the degree

of precision you need to measure to.

The type of data you have affects how you find probabilities.

So far we’ve only looked at probability distributions that deal with discrete data.

Using these probability distributions, we’ve been able to find the probabilities of

exact discrete values.

The problem is that a lot of real-world problems involve continuous data, and

discrete probability distributions just don’t work with this sort of data. To find

probabilities for continuous data, you need to know about continuous data and

continuous probability distributions.

Meanwhile, someone has a problem...

Continuous data is like a

smooth, continuous path

you can cycle along.

Continuous data can

take countless values.

1 2 3 4 5

328 Chapter 8

What’s the delay?

Julie is a student, and her best friend keeps trying to get her fixed up on

blind dates in the hope that she’ll find that special someone. The only

trouble is that not many of her dates are punctual—or indeed turn up.

Julie hates waiting alone for her date to arrive, so she’s made herself a rule:

if her date hasn’t turned up after 20 minutes, then she leaves.

I have another date tonight.

I definitely won’t wait for more than 20

minutes, but I hate standing around, What’s

the probability I’ll be left waiting for more

than 5 minutes? Can you help?

Minutes

Frequency

This is when

Julie arrives.

This is when Julie leaves.

Here’s a sketch of the frequency showing the amount of time Julie

spends waiting for her date to arrive:

We need to find probabilities for the amount of time Julie spends waiting for

her date. Is the amount of time discrete or continuous? Why? How do you

think we can go about finding probabilities?

Statsville men on blind dates aren’t

punctual; they could arrive at any time.

frequency and continuous data

Meet Julie, a girl on a mission

to find the perfect partner

for herself.

you are here 4 329

using the normal distribution

We need to find the probability that Julie will have to wait for more than 5

minutes for her date to turn up. The trouble is, the amount of time Julie has to

wait is continuous data, which means the probability distributions we’ve learned

thus far don’t apply.

When we were dealing with discrete data, we were able to produce a specific

probability distribution. We could do this by either showing the probability of

each value in a table, or by specifying whether it followed a defined probability

distribution, such as the binomial or Poisson distribution. By doing this, we

were able to specify the probability of each possible value. As an example, when

we found the probability distribution for the winnings per game for one of Fat

Dan’s slot machines, we knew all of the possible values for the winnings and

could calculate the probability of each one..

With discrete data, we could give

the probability of each value.

For continuous data, it’s a different matter. We can no longer give the probability

of each value because it’s impossible to say what each of these precise values is.

As an example, Julie’s date might turn up after 4 minutes, 4 minutes 10 seconds,

or 4 minutes 10.5 seconds. Counting the number of possible options would be

impossible. Instead, we need to focus on a particular level of accuracy and the

probability of getting a range of values.

I get it. For discrete probability

distributions, we look at the probability of

getting a particular value; for continuous

probability distributions, we look at the

probability of getting a particular range.

x -1 4 9 14 19

P(X = x)

0.977 0.008 0.008 0.006 0.001

We need a probability distribution for continuous data

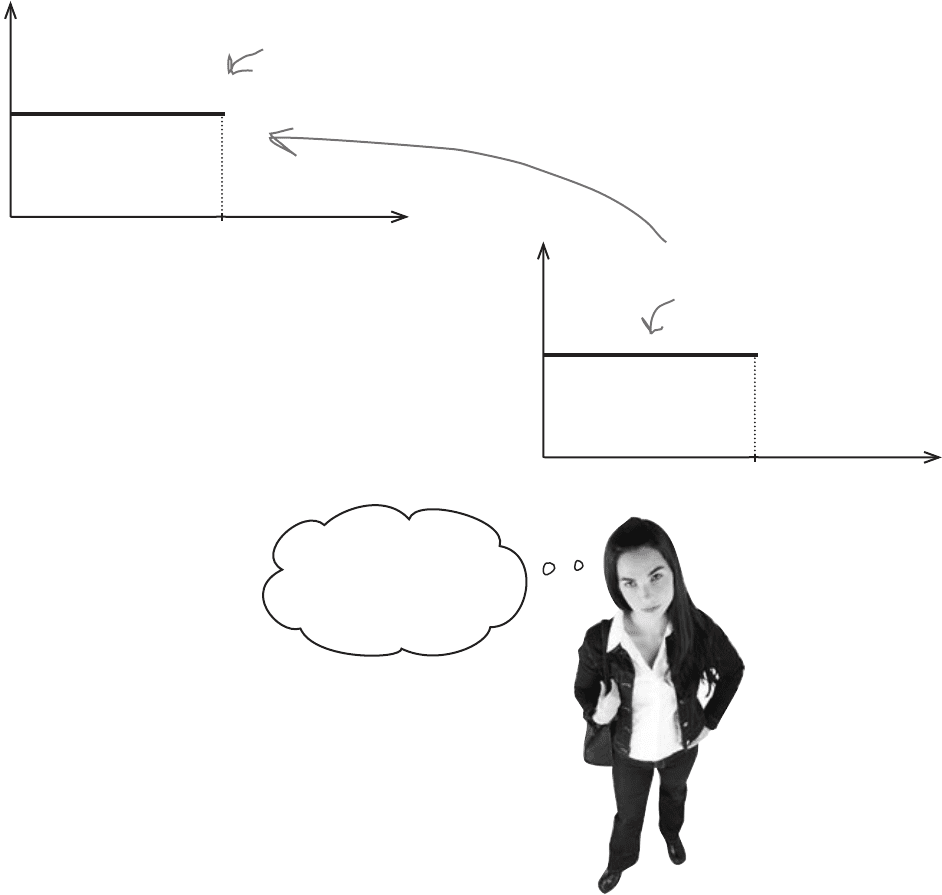
330 Chapter 8

We can describe the probability distribution of a continuous random

variable using a probability density function.

A probability density function f(x) is a function that you can use to find the

probabilities of a continuous variable across a range of values. It tells us

what the shape of the probability distribution is.

Here’s a sketch of the probability density function for the amount of time

Julie spends waiting for her date to turn up:

This line is the probability density function for

the amount of time Julie waits for her dates.

The probability is constant for the first 20

minutes, and then it drops to 0 because she leaves.

Hello? I thought we

were going to find

some probabilities.

How does this help?

Can you see how it matches the shape of the frequency? This isn’t

just a coincidence.

Probability is all about how likely things are to happen, and the

frequency tells you how often values occur. The higher the relative

frequency, the higher the probability of that value occurring. As

the frequency for the amount of time Julie has to wait is constant

across the 20 minute period, this means that the probability density

function is constant too.

These are the

same basic shape.

Minutes

Frequency

f(x)

probability density functions

Probability density functions can be used for continuous data