Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 391

Now let’s try using the normal approximation to the binomial and check that we get the same

result. First of all, if X ~ B(12, 0.5), what normal distribution can we use to approximate this?

Once you’ve found that, what’s P(X < 6)?

392 WHO WANTS TO WIN A SWIVEL CHAIR

To find individual probabilities, we use the formula

P(X = r) =

n-r

where

We need to find P(X < 6) where X ~ B(12, 0.5). To do this, we need to find

P(X = 0) through P(X = 5), and then add all the probabilities together.

The individual probabilities are

= n!

r!(n - r)!

P(X = 0) =

x 0.5

= 0.5

P(X = 1) =

x 0.5 x 0.5

= 12 x 0.5

P(X = 2) =

x 0.5

= 66 x 0.5

P(X = 3) =

x 0.5

= 220 x 0.5

P(X = 4) =

x 0.5

= 495 x 0.5

P(X = 5) =

x 0.5

= 792 x 0.5

Adding these together gives us an overall probability of

P(X < 6) = (1 + 12 + 66 + 220 + 495 + 792) x 0.5

= 1586 x 0.5

= 0.387 (to 3 decimal places)

Before we use the normal distribution for the full 40 questions for Who Wants To Win A Swivel

Chair, let’s tackle a simpler problem to make sure it works. Let’s try finding the probability that

we get 5 or fewer questions correct out of 12, where there are only two possible choices for

each question.

Let’s start off by working this out using the binomial distribution. Use the binomial distribution

to find P(X < 6) where X ~ B(12, 0.5).

you are here 4 393

What do you think could have gone wrong? How

do you think we could fix it?

Did I miss something?

In what way was that a

good approximation?

The two methods of calculating the probability have given

quite different results.

Using the binomial distribution, P(X < 6) comes to 0.387, but using the normal

distribution it comes to 0.5. We should have been able to use the normal

distribution in place of the binomial, but the results aren’t close enough.

Now let’s try using the normal approximation to the binomial and check we get the same result.

First of all, if X ~ B(12, 0.5), what normal distribution can we use to approximate this? Once

you’ve found that, what’s P(X < 6)?

X ~ B(12, 0.5), which means that n = 12, p = 0.5 and q = 0.5. A good approximation to this is

X ~ N(np, npq), or X ~ N(6, 3).

We want to find P(X < 6), so we start by calculating the standard score.

z = x - μ

= 6 - 6

= 0

Looking this up in probability tables gives us

P(X < 6) = 0.5

394 WHO WANTS TO WIN A SWIVEL CHAIR

Revisiting the normal approximation

So what went wrong? Let’s take a closer look at the problem and see if we can

figure out what happened and also what we can do about it.

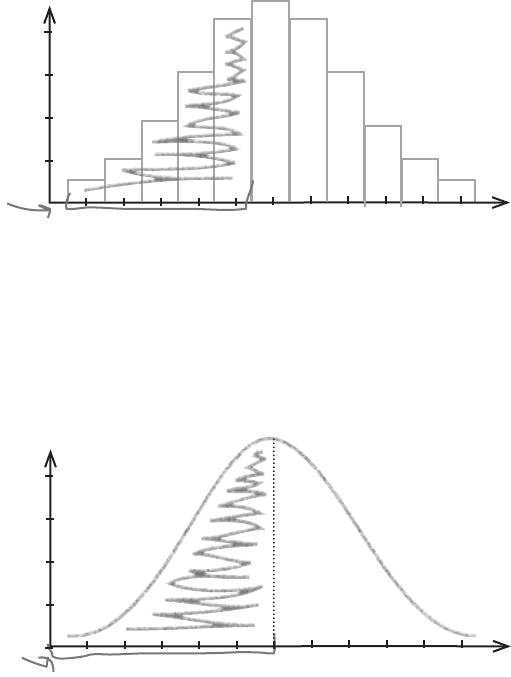
First off, here’s the probability distribution for X ~ B(12, 0.5). We wanted to find

the probability of getting fewer than 6 questions correct, and we achieved this by

calculating P(X < 6).

We then approximated the distribution by using X ~ N(6, 3), and as needed to find

P(X < 6) for the binomial distribution, we calculated P(X < 6) using the normal

distribution:

Take a really close look at the two probability distributions. It’s tricky to spot, but

there’s a crucial difference between the two—the ranges we used to calculate the

two probabilities are slightly different. We actually used a slightly larger range when

we used the normal distribution, and this accounts for the larger probability.

We’ll look at this in more detail on the next page.

P(X < 6) is this area here.

0.1

0.5

0.15

1 2 3 4 5

0.20

7 8 9 10 11

0.1

0.5

0.15

1 2 3 4 5

0.20

7 8 9 10

We found P(X < 6)

by adding all these

together.

you are here 4 395

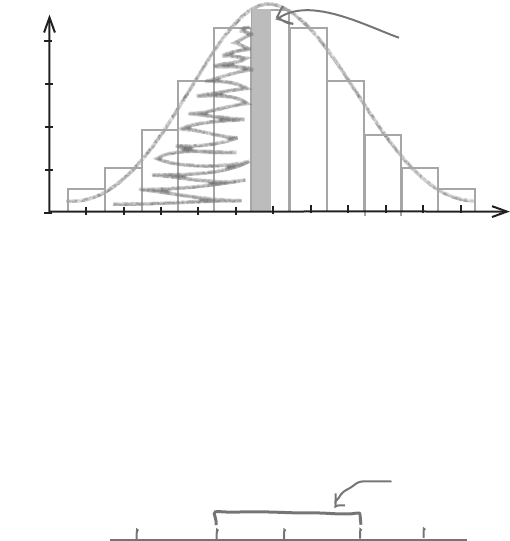
5 5.5 6 6.5 7

Can you see where the problem lies?

When we take integers from a discrete probability distribution and translate them onto a

continuous scale, we don’t just look at those precise values in isolation. Instead, we look

at the range of numbers that round to each of the values.

Let’s take the discrete value 6 as an example. When we translate the number 6 to a

continuous scale, we need to consider all of the numbers that round to it—in other

words, the entire range of numbers from 5.5 to 6.5.

There’s one thing we overlooked when we calculated the two probabilities—we didn’t

make allowances for one distribution being discrete (the binomial), and the other being

continuous (the normal). This is important, as the probability range we use can make a

big difference to the resulting probabilities.

Here are the probability distributions for X ~ B(12, 0.5) and N(6, 3), both shown on the

same chart. We’ve highlighted where the probability range we used with the normal

distribution extends beyond the range we used for the binomial distribution.

All of these

values round to 6.

So how does this apply to our probability problem?

When we tried using the normal distribution to approximate the probability of getting

fewer than 6 questions correct, we didn’t look at how the discrete value 6 translates onto a

continuous scale. The discrete value 6 actually covers a range from 5.5 to 6.5, so instead of

using the normal distribution to find P(X < 6), we should have tried calculating

P(X < 5.5) instead.

This adjustment is called a continuity correction. A continuity correction is the small

adjustment that needs to be made when you translate discrete values onto a continuous scale.

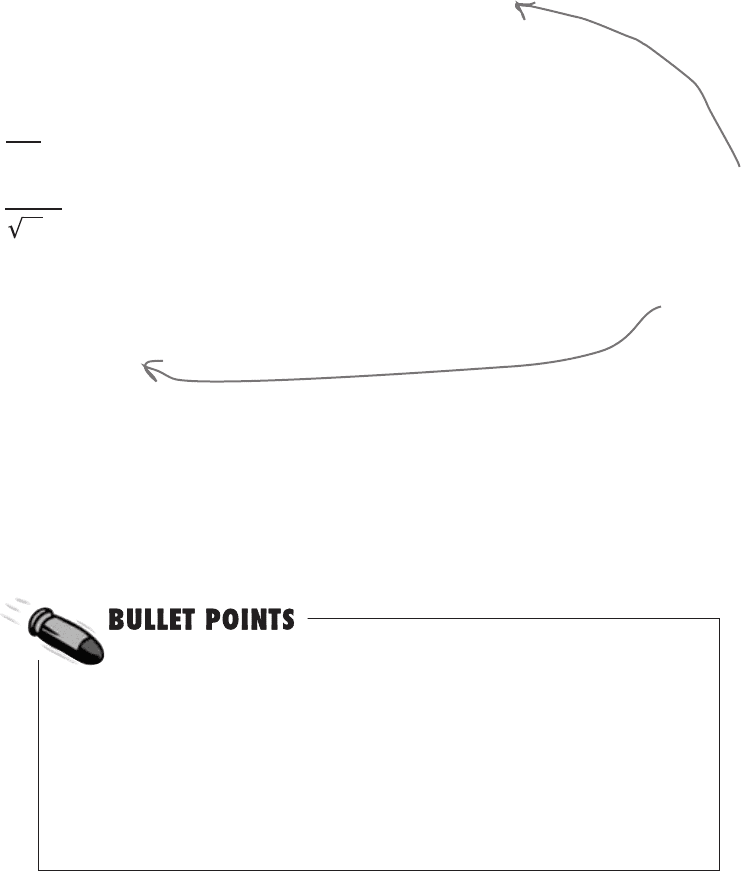
The binomial is discrete, but the normal is continuous

We didn’t include this area when we calculated

P(X < 6) using the binomial distribution, but we

did when we calculated P(X < 6) using the normal

distribution.

0.1

0.5

0.15

1 2 3 4 5

0.20

7 8 9 10 11

396 WHO WANTS TO WIN A SWIVEL CHAIR

Let’s try finding P(X < 5.5) where X ~ N(6, 3), and see how good an approximation

this is for the probability of getting five or fewer questions correct. Using the binomial

distribution we found that the probability we’re aiming for is around 0.387.

Let’s see how close an approximation the normal distribution gives us.

We want to find P(X < 5.5) where X ~ (6, 3), so let’s start by calculating the standard score.

z = x - μ

= 5.5 - 6

= -0.29 (to 2 decimal places)

We want to find the probability given by the area Z < -0.29, and looking this up in

standard normal probability tables gives us a probability of 0.3859. In other words,

P(X < 5.5) = 0.3859

This is really close to the probability we came up with using the binomial distribution. The

binomial distribution gave us a probability of 0.387, so the normal distribution gives us a

pretty close approximation.

In particular circumstances you can

use the normal distribution to

approximate the binomial. If

X ~ B(n, p) and np > 5 and nq > 5

then you can approximate X using

X ~ N(np, npq)

 If you’re approximating the binomial

distribution with the normal

distribution, then you need to apply a

continuity correction to make sure

your results are accurate.



Look at these two

probabilities. They’re

really close, so it looks

like the continuity

correction did the trick.

Apply a continuity correction before calculating the approximation

you are here 4 397

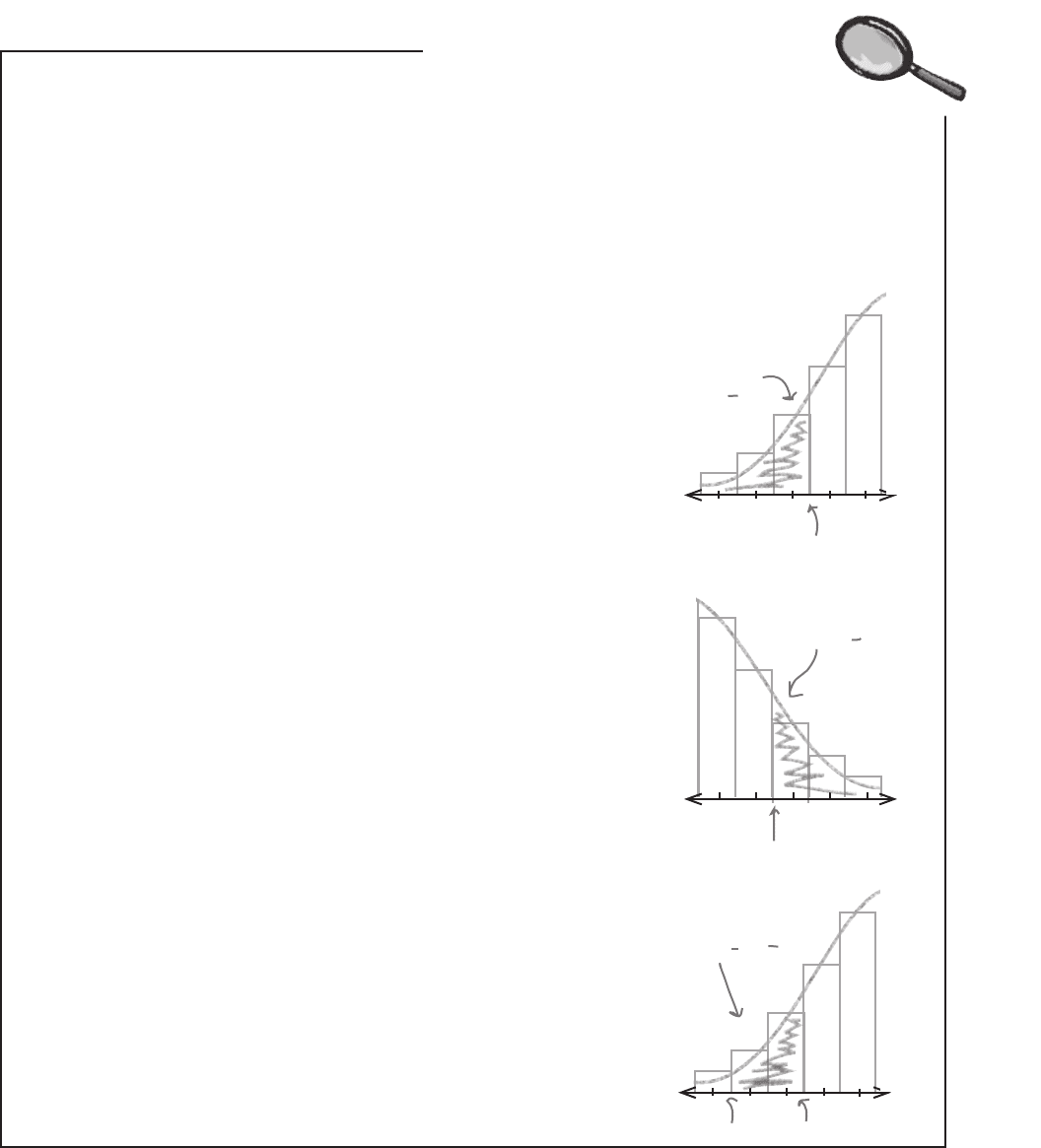
You need to use

P(X < 3.5) to

approximate

P(X < 3).

1 2 3 4

1.5

3.5

The big trick with using the normal distribution to approximate binomial probabilities

is to make sure you apply the right continuity correction. As you’ve seen, small

changes in the probability range you choose can lead to significant errors in the actual

probabilities. This might not sound like too big a deal, but using the wrong probability

could lead to you making the wrong decisions.

Let’s take a look at the kinds of continuity corrections you need to make for different

types of probability problems.

Finding ≤ probabilities

When you work with probabilities of the form P(X ≤ a), the key thing you

need to make sure of is that you choose your range so that it includes the

discrete value a. On a continuous scale, the discrete value a goes up to

(a + 0.5). This means that if you’re using the normal distribution to find

P(X ≤ a), you actually need to calculate P(X < a + 0.5) to come up with a

good approximation. In other words, you add an extra 0.5.

Finding “between” probabilities

Probabilities of the form P(a ≤ X ≤ b) need continuity corrections to make

sure that both a and b are included. To do this, we need to extend the range

out by 0.5 either side. To approximate this probability using the normal

distribution, we need to find P(a - 0.5 < X < b + 0.5). This is really just a

combination of the two types above.

3.5

7 8 9 10 11

8.5

Finding ≥ probabilities

If you need to find probabilities of the form P(X ≥ b), you need to make

absolutely sure that your range includes the discrete value b. The value b

extends down to (b - 0.5) on a continuous scale so you need to use a range of

P(X > b - 0.5) to make sure that you include it. In other words, you need to

subtract an extra 0.5.

This time, we subtract

0.5 and use P(X > 8.5)

to find P(X > 9).

We use P(1.5 < X < 3.5)

to find P(2 < X < 3).

Continuity Corrections Up Close

398 WHO WANTS TO WIN A SWIVEL CHAIR

Does it really save time to

approximate the binomial distribution

with the normal?

A: It can save a lot of time. Calculating

binomial probabilities can be time-consuming

because you generally have to work out the

probability of lots of different values. You

have no way of simply calculating binomial

probabilities over a range of values.

If you approximate the binomial distribution

with the normal distribution, then it’s a lot

quicker. You can look probabilities up in

standard tables and also deal with whole

ranges at once.

So is it really accurate?

A:Yes, It’s accurate enough for most

purposes. The key thing to remember is that

you need to apply a continuity correction.

If you don’t then your results will be less

accurate.

What about continuity corrections

for < and >? Do I treat those the same

way as the ones for ≤ and ≥?

A: There’s a difference, and it all comes

down to which values you want to include

and exclude.

When you’re working out probabilities using

≤ and ≥, you need to make sure that you

include the value in the inequality in your

probability range. So if, say, you need to

work out P(X ≤ 10), you need to make sure

your probability includes the value 10. This

means you need to consider P(X < 10.5).

When you’re working out probabilities using

< or >, you need to make sure that you

exclude the value in the inequality from your

probability range. This means that if you

need to work out P(X < 10), you need to

make sure that your probability excludes 10.

You need to consider P(X < 9.5).

You can approximate the binomial

distribution with both the normal and

Poisson distributions. Which should I

use?

A: It all depends on your circumstances.

If X ~ B(n, p), then you can use the normal

distribution to approximate the binomial

distribution if np > 5 and nq > 5.

You can use the Poisson distribution to

approximate the binomial distribution if

n > 50 and p < 0.1

Remember, you need to apply a continuity correction when you

approximate the binomial distribution with the normal distribution.

you are here 4 399

Pool Puzzle

Your job is to take snippets from the

pool and place them into the blank

lines so that you get the right

continuity correction for each

dscrete probability range. You

may use the same snippet more

than once, and you won’t need to

use all the snippets.

Note: each thing from

the pool can be used

more than once!

X < 3

X > 3

X ≥ 3

X ≤ 3

X > 0

X = 0

3 ≤ X ≤ 10

3 < X ≤ 10

3 ≤ X < 10

3 < X < 10

2.5

10.5

9.5

0.5

3.5

10.5

0.5

2.5

9.5

400 WHO WANTS TO WIN A SWIVEL CHAIR

Pool Puzzle

Your job is to take snippets from the

pool and place them into the blank

lines so that you get the right

continuity correction for each

dscrete probability range. You

may use the same snippet more

than once, and you won’t need to

use all the snippets.

Note: each thing from

the pool can be used

more than once!

X < 3

X > 3

X ≥ 3

X ≤ 3

X > 0

X = 0

3 ≤ X ≤ 10

3 < X ≤ 10

3 ≤ X < 10

3 < X < 10

< <

2.5

3.5

2.5

3.5

9.5

0.5-

0.5

3.5

2.5

10.5

0.5

3.5

9.5

All the numbers from -0.5

to 0.5 round to 0, so they

must be included in the

range.

Here, we’re looking

for values less than

3. 2.5 rounds to 3,

so we only want to

include values less

than 2.5 in

our range.

Here, we’re looking

for values less

than or equal to

3. All the numbers

between 2.5 and

3.5 round to 3, so

we need to include

values less than

3.5 in our range.

< 10.5X