Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 411

using the normal distribution ii

It’s time to test your statistical knowledge. Complete the table below, saying what normal

distribution suits each situation, and what conditions there are.

Situation Distribution Condition

X + Y

X ~ N(μ

, σ

), Y ~ (μ

, σ

)

X + Y ~ N(μ

+ μ

, σ

+ σ

)

X, Y are independent

X - Y

X ~ N(μ

, σ

), Y ~ (μ

, σ

)

X - Y ~ N(μ

- μ

, σ

+ σ

)

X, Y are independent

aX + b

X ~ N(μ, σ

)

aX + b ~ N(aμ + b, a

)

a, b are constant values

+ X

+ ... + X

X ~ N(μ, σ

)

+ X

+ ... + X

~ N(nμ, nσ

)

, X

, ..., X

are independent

observations of X

Normal approximation of X

X ~ B(n, p)

X ~ N(np, npq)

np > 5, npq > 5

Continuity correction required

Normal approximation of X

X ~ Po(λ)

X ~ N(λ, λ)

λ > 15

Continuity correction required

412 Chapter 9

You can approximate the binomial

and Poisson distributions with the

normal, but what about the geometric

disribution? Can the normal distribution

ever approximate that?

A: We were able to use the normal

distribution in place of the binomial and

Poisson distributions because under

particular circumstances, these distributions

adopt the same shape as the normal.

The geometric distribution, on the other hand,

never looks like the normal, so the normal

can never effectively approximate it.

Do I have to use a continuity

correction if I approximate the Poisson

distribution with the normal distribution?

A: Yes. This is because you’re

approximating a discrete probability

distribution with a continuous one. This

means that you need to apply a continuity

correction, just as you would for the binomial

distribution.

What’s the advantage of

approximating the binomial or poisson

distribution with the normal? Won’t my

results be more accurate if I just use the

original distribution?

A: Your results will be more accurate if

you use the original distribution, but using

them can be time consuming. If you wanted

to find the probability of a range of values

using the binomial or poisson distribution,

you’d need to find the probability of every

single value within that range. Using the

normal distribution, on the other hand, you

can look up probabilities for whole ranges,

and so they’re a lot easier to find.

In particular circumstances you

can use the normal distribution to

approximate the Poisson.

If X ~ Po(λ) and λ > 15 then you can

approximate X using X ~ N(λ, λ)



If you’re approximating the Poisson

distribution with the normal

distribution, then you need to apply

a continuity correction to make sure

your results are accurate.



Use a continuity correction if you approximate the Poisson distribution

with the normal distribution.

bullet points and no dumb questions

you are here 4 413

using the normal distribution ii

A runaway success!

Thanks to your savvy statistical analysis,the Love Train is open for business, and

demand has outstripped Dexter’s highest expectations. Here are some of Dexter’s

happy customers:

this is a new chapter 415

using statistical sampling

Taking Samples

Statistics deal with data, but where does it come from?

Some of the time, data’s easy to collect, such as the ages of people attending a health

club or the sales figures for a games company. But what about the times when data isn’t

so easy to collect? Sometimes the number of things we want to collect data about are so

huge that it’s difficult to know where to start. In this chapter, we’ll take a look at how you

can effectively gather data in the real world, in a way that’s efficient, accurate, and can

also save you time and money to boot. Welcome to the world of sampling.

Statistics deal with data, but where does it come from?

Some of the time, data’s easy to collect, such as the ages of people attending a health

club or the sales figures for a games company. But what about the times when data isn’t

so easy to collect? Sometimes the number of things we want to collect data about are so

huge that it’s difficult to know where to start. In this chapter, we’ll take a look at how you

can effectively gather data in the real world, in a way that’s efficient, accurate, and can

also save you time and money to boot. Welcome to the world of sampling.

Stay nice and relaxed,

and this won’t hurt a bit.

416 Chapter 10

Please, no more gumballs!

I’m running out of teeth

Well, gumball #1,466 ran

out of flavor after 55 minutes,

but gumball #1,467 is still going

strong after an hour...

The Mighty Gumball taste test

Mighty Gumball is the leading vendor of a wide variety of candies and chocolates. Their

signature product is their super-long-lasting gumball. It comes in all sorts of colors to suit

all tastes.

Mighty Gumball plans to run a series of television commercials to attract even more

customers, and as part of this, they want to advertise just how long the flavor of their

gumballs lasts for. The problem is, how do they get the data?

They’ve decided to implement a taste test, and they’ve hired a bunch of tasters to help

with the tests. There are just two problems: the tasters are using up all of the gumballs,

and their dental plans are costing the company a fortune.

mighty gumball’s flavor dilemma

you are here 4 417

using statistical sampling

They’re running out of gumballs

The fatal flaw with the Mighty Gumball taste test is that the tasters are trying out

all of the gumballs. Not only is this having a bad effect on the tasters’ teeth, it

also means that there are no gumballs left to sell. After all, they can hardly reuse

their gumballs once the tasters have finished with them.

The whole point of the taste test is for Mighty Gumball to figure out how long

the flavor lasts for. But does this really mean that the tasters have to try out every

single gumball?

What would you do to establish how long the gumball

flavor lasts for? What do you need to consider? Write

your answer below in as much detail as possible.

Mighty Gumball, Inc.

418 Chapter 10

Mighty Gumball is running into problems because they’re tasting every single gumball

as part of their taste test. It’s costing them time, money, and teeth, and they have no

gumballs left to actually sell to their customers.

So what should Mighty Gumball do differently? Let’s start by looking at the difference

between populations and samples.

Gumball samples

You don’t have to taste every gumball to get an idea of how long the

flavor lasts for. Instead of testing the entire population, you can test a

sample instead.

A statistical sample is a selection of items taken from a population. You

choose your sample so that it’s fairly representative of the population as a

whole; it’s a representative subset of the population. For Mighty Gumball,

a sample of gumballs means just a small selection of gumballs rather

than every single one of them.

A study or survey involving just a sample of the population is called a

sample survey. A lot of the time, conducting a survey is more practical

than a census. It’s usually less time-consuming and expensive, as you don’t

have to deal with the entire population. And because you don’t use the

whole population, taking a sample survey of the gumballs means that

there’ll be plenty left over when you’re done.

Gumball populations

At the moment, Mighty Gumball is carrying out their taste test using every single

gumball that they have available. In statistical terms, they are conducting their test

using an entire population.

A statistical population refers to the entire group of things that you’re trying to

measure, study, or analyze. It can refer to anything from humans to scores to gumballs.

The key thing is that a population refers to all of them.

A census is a study or survey involving the entire population, so in the case of Mighty

Gumball, they’re conducting a census of their gumball population by tasting every

single one of them. A census can provide you with accurate information about your

population, but it’s not always practical. When populations are large or infinite, it’s

just not possible to include every member.

So how can you use samples to find out about a population? Let’s see.

A population of gumballs

refers to all of them.

A sample is a

subset of the

population, so

just some of

the gumballs.

populations vs. samples

Test a gumball sample, not the whole gumball population

you are here 4 419

using statistical sampling

How sampling works

The key to creating a good sample is to choose one that is as close a match to your

population as possible. If your sample is representative, this means it has similar

characteristics to the population. And this, in turn, means that you can use your

sample to predict what characteristics the population will have.

Suppose you use a representative sample of gumballs to test how long the flavor of

each gumball lasts for. The distribution of the results might look something like this:

Population Chart

duration

frequency

Sampling Chart

duration

frequency

Here’s the chart for the population. Can you

see how closely the sample and population

distributions agree?

If you compare the two charts, the overall shape

is very similar, even though one is for all of the

gumballs and the other is for just some of them.

They share key characteristics such as where the

center of the data is, and this means you can use

the sample data to make predictions about the

population.

Most of the gumballs

last for this long

Although it’s not

exactly the same, the

results of the gumball

population are a

similar shape to that

of the sample.

Even though you’ve only tried a small sample of

gumballs, you still have an impression of the shape

of the distribution, and the more gumballs you try,

the clearer the shape is. As an example, you can

get a rough impression of where the center of the

population distribution is by looking at the shape of

the sample distribution.

Let’s compare this with the actual population:

So are you saying that

all samples resemble

their parent populations?

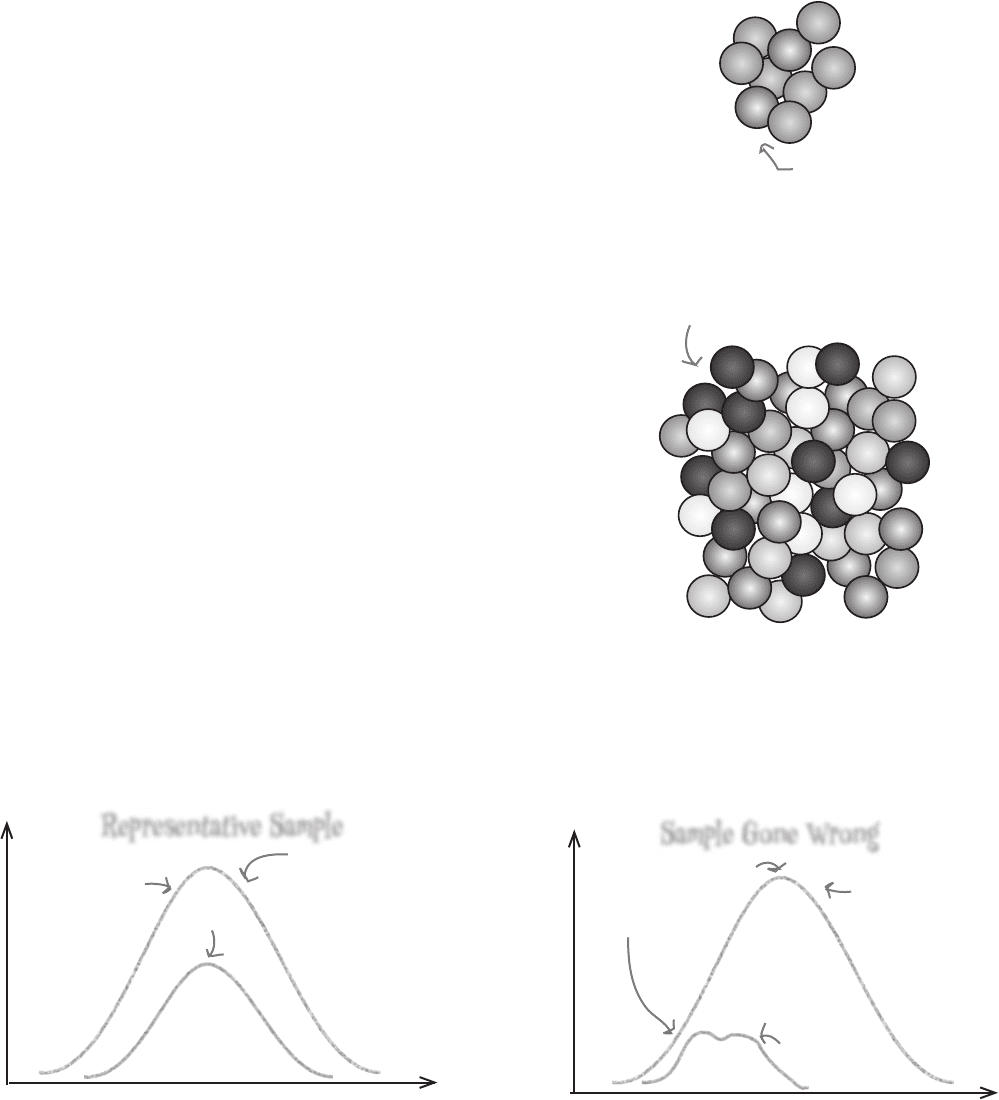
420 Chapter 10

When sampling goes wrong

If only we could guarantee that every sample was a close match to the

population it comes from. Unfortunately, not every sample closely resembles its

population. This may not sound like a big deal, but using a misleading sample

can actually lead you to draw the wrong conclusions about your population.

As an example, imagine if you took a sample of gumballs to find out how long

flavor typically lasts for, but your sample only contained red gumballs. Your

sample might be representative of red gumballs, but not so representative of

all gumballs in the population. If you used the results of this sample to gather

information about the general gumball population, you could end up with a

misleading impression about what gumballs are generally like.

Sample Gone Wrong

duration

frequency

Representative Sample

duration

frequency

Sample and population

are distributed

differently.

Sample and

population have a

similar shape.

Using the wrong sample could lead you to draw wrong conclusions about

population parameters, such as the mean or standard deviation. You might be left

with a completely different view of your data, and this could lead you to make

the wrong decisions.

The trouble is, you might not know this at the time. You might think your

population is one thing when in fact it’s not. We need to make sure we have some

mechanism for making sure our samples are a reliable representation of the

population.

We want this:

Instead of this:

This sample…

…might not be the most

accurate representation of this

population.

not all samples are reliable

Sample

Population

Sample

Population