Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

this is a new chapter 441

estimating populations and samples

Making Predictions

...I mean, men! They’re all

the same. Once you’ve met

one, you’ve met them all!

Wouldn’t it be great if you could tell what a population was

like, just by taking one sample?

Before you can claim full sample mastery, you need to know how to use your samples

to best effect once you’ve collected them. This means using them to accurately predict

what the population will be like and coming up with a way of saying how reliable your

predictions are. In this chapter, we’ll show you how knowing your sample helps you get to

know your population, and vice versa.

442 Chapter 11

So how long does flavor really last for?

With your help, Mighty Gumball has pulled together an unbiased

sample of super-long-lasting gumballs. They’ve tested each of the

gumballs in the sample and collected lots of data about how long

gumball flavor within the sample lasts.

There’s just one problem...

I don’t care how long flavor lasts in the sample.

What I do care about is flavor duration in the

population. That way, I can say how much longer our

gumballs last than the competing brand.

To satisfy the CEO, we’re going to need to find both the mean

and the variance of flavor duration in the whole Mighty Gumball

population.

Here’s the data we gathered from the sample. How do you think

we can use it to tell us what the mean of the population is?

Take a look at the data. How would you use this data to estimate the mean

and variance of the population? How reliable do you think your estimate will

be? Why?

61.9 62.6 63.3 64.8 65.1

66.4 67.1 67.2 68.7 69.9

Here’s how long

flavor lasts for

in minutes

making estimates using a sample

Mighty Gumball’s pugilistic CEO

you are here 4 443

estimating populations and samples

So how can we use the results of the sample taste test to tell us the mean

amount of time gumball flavor lasts for in the general gumball population?

The answer is actually pretty intuitive. We assume that the mean flavor

duration of the gumballs in the sample matches that of the population. In

other words, we find the mean of the sample and use it as the mean for the

population too.

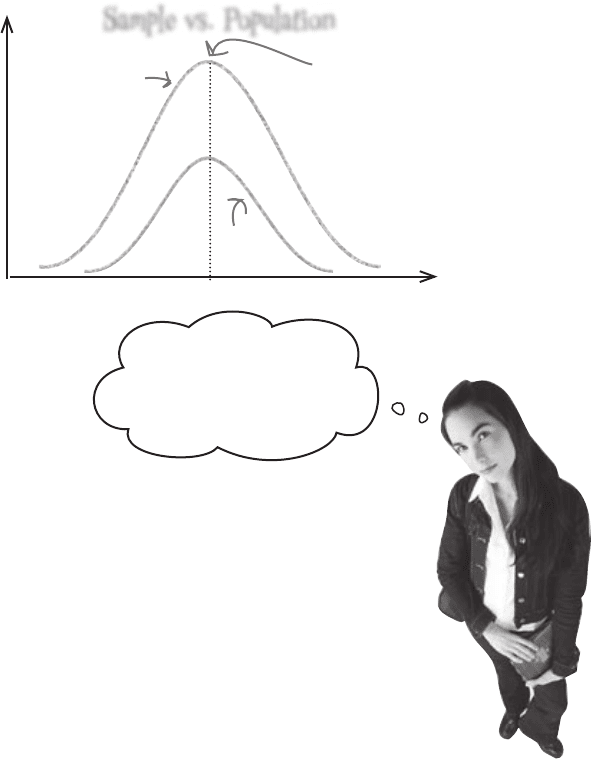
Here’s a sketch showing the distribution of the sample, and what you’d

expect the distribution of the population to look like based on the sample.

You’d expect the distribution of the population to be a similar shape to

that of the sample, so you can assume that the mean of the sample and

population have about the same value.

So are you saying that

the mean of the sample

exactly matches the mean

of the population?

We can’t say that they exactly match, but

it’s the best estimate we can make.

Based on what we know, the mean of the sample is the best

estimate we can make for the mean of the population. It’s

the most likely value for the population mean that we can

come up with based on the information that we have.

The mean of the sample is called a point estimator for

the population mean. In other words, it’s a calculation

based on the sample data that provides a good estimate for

the mean of the population.

You’d expect the

population and sample mean

to be about the same

Sample vs. Population

flavor duration

frequency

Sample

Population

Let’s start by estimating the population mean

444 Chapter 11

Up until now, we’ve been dealing with actual values of population parameters

such as the mean, μ, or the variance, σ

. We’ve either been able to calculate

these for ourselves, or we’ve been told what they are.

This time around we don’t know the exact value of the population parameters.

Instead of calculating them using the population, we estimate them using

the sample data instead. To do this, we use point estimators to come up with a

best guess of the population parameters.

A point estimator of a population parameter is some function or calculation

that can be used to estimate the value of the population parameter. As an

example, the point estimator of the population mean is the mean of the sample,

as we can use the sample mean to estimate the population mean.

Point estimators use

sample data...

...to estimate the

population parameters.

We differentiate between an actual population parameter and its point

estimator using the ^ symbol. As an example, we use the symbol μ to represent

the population mean, and to represent its estimator. So to show that you’re

dealing with the point estimator of a particular population parameter, take the

symbol of the population parameter, and top it with a ^.

I’m the population

mean, the real thing.

See this hat I’m wearing?

It means I’m a point estimator.

If you don’t have the exact

value of the mean, then I’m the

next best thing.

The point estimator for the

population mean looks like the mean

itself, except it’s topped with a ^.

Point estimators can approximate population parameters

all about point estimators

you are here 4 445

estimating populations and samples

x = Σx

x is the mean of

the sample.

Add together the numbers

in the sample, and divide by

how many there are.

It occurs to me that we have a

symbol for the population mean and

one for its point estimator. Is there

a symbol for the sample mean too?

There’s a shorthand way of writing the sample mean.

The symbol μ has a very precise meaning. It’s the mean of the population.

We have a different way to represent the mean of the sample so that we

don’t get confused about which mean we’re talking about. To represent the

sample mean, we use the symbol x (pronounced “x bar”). That way, we

know that if someone refers to μ, they’re referring to the population mean,

and if they refer to x, they’re referring to the sample mean.

x is the sample equivalent of μ, and you calculate it in the same way you

would the population mean. You add together all the data in your sample,

and then divide by however many items there are. In other words, if your

sample size is n,

We can use this to write a shorthand expression for the point estimator for

the population. Since we can estimate the population mean using the mean

of the sample, this means that

= x

Use the sample data to estimate the value of the population

mean. Here’s a reminder of the data:

61.9 62.6 63.3 64.8 65.1 66.4 67.1 67.2 68.7 69.9

We estimate the mean

of the population...

...using the mean of the sample.

446 Chapter 11

Use the sample data to estimate the value of the population

mean. Here’s a reminder of the data:

Surely the mean is just the mean.

Why are there so many different symbols

for it?

A: There are three different concepts at

work. There’s the mean of the population,

the mean of the sample, and the point

estimator for the population mean.

The population mean is represented

by μ. This is the sort of mean that we’ve

encountered throughout the book so far, and

you find it by adding together all the data in

the population and dividing by the size of the

population.

The sample mean is represented by x.

You find it in the same way that you find μ,

except that this time your data comes from

a sample. To calculate x, you add together

the data in your sample, and divide by the

size of it.

The point estimator for μ is represented by

μ. It’s effectively a best guess for what you

think the population mean is, based on the

sample data.

So does that mean that we can find

μ by just taking the mean of a sample?

A: We can’t find the exact value of

μ using a sample, but if the sample is

unbiased, it gives us a very good estimate.

In other words, we can use the sample data

to find μ, not the true value of μ itself.

But what about if the sample is

biased? How do we come up with an

estimate for μ then?

A: This is where it’s important to make

your sample as unbiased as possible. If all

the data you have comes from your sample,

then that’s what you need to use as the

basis for your estimate. If your sample is

biased, then this means that your estimate

for μ is likely to be inaccurate, and it may

lead you into making wrong decisions.

Does the size of the sample matter?

A: In general, the larger the size of

your sample, the more accurate your point

estimator is likely to be.

61.9 62.6 63.3 64.8 65.1 66.4 67.1 67.2 68.7 69.9

We can estimate the population mean by calculating the mean of the sample.

μ = x = 61.9 + 62.6 + 63.3 + 64.8 + 65.1 + 66.4 + 67.1 + 67.2 + 68.7 + 69.9

= 657/10

= 65.7

solutions and questions

μ is the mean of the

population, x is the

mean of the sample,

and μ is the point

estimator for μ.

you are here 4 447

estimating populations and samples

A point estimator is an estimate for the value of a

population parameter, derived from sample data.

The ^ symbol is added to the population parameter

when you’re talking about its point estimator. As an

example, the point estimator for μ is μ.

The mean of a sample is represented as x. To find the

mean of the sample, use the formula

x = Σx

where x represents the values in the sample, and n is

the sample size.



The point estimator for the population mean is found by

calculating x. In other words,

μ = x

This means that if you want a good estimate for the true

value of the population mean, you can use the mean of

the sample.



This looks great! We can use your

work in our television commercials to say

how long gumball flavor lasts for, and it

beats our main rival, hands down. Just one

question: how much variation do you expect

there to be?

You’ve come up with a good estimate

for the population mean, but what

about the variance?

If we can come up with a good estimate for the

population variance, then the CEO will be able to

tell how much variation in flavor duration there’s

likely to be in the gumball population, based on

the results of the sample data.

448 Chapter 11

The variance of the data in the sample may not be

the best way of estimating the population variance.

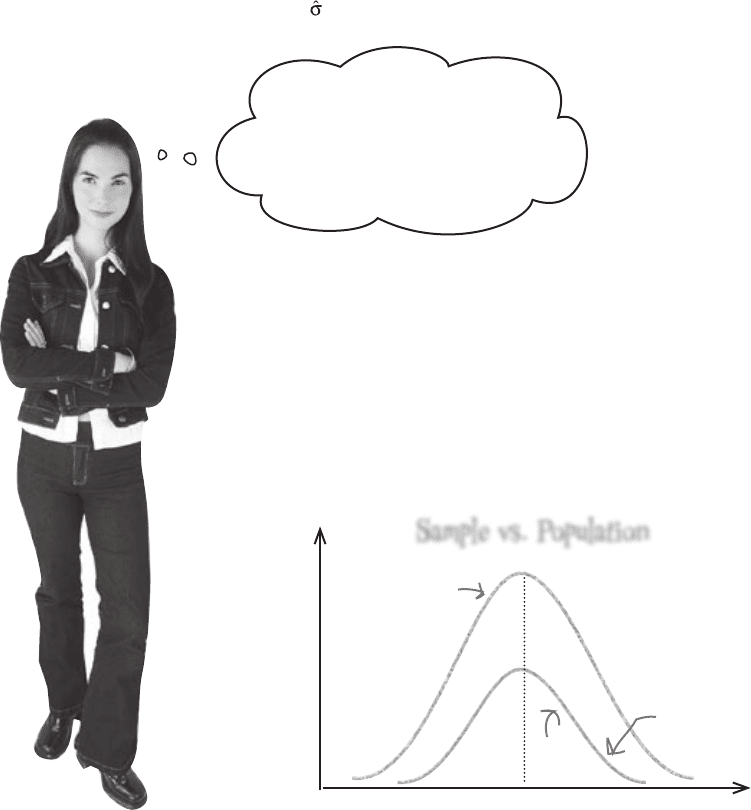
You already know that the variance of a set of data measures the way in

which values are dispersed from the mean. When you choose a sample,

you have a smaller number of values than with the population, and since

you have fewer values, there’s a good chance they’re more clustered

around the mean than they would be in the population. More extreme

values are less likely to be in your sample, as there are generally fewer of

them.

That’s easy. The variance of the

sample is bound to be the same

as that of the population. We can

use the sample variance to estimate

the population variance.

Let’s estimate the population variance

So far we’ve seen how we can use the sample mean to estimate the mean

of the population. This means that we have a way of estimating what the

mean flavor duration is for the super-long-lasting gumball population.

To satisfy the Mighty Gumball CEO, we also need to come up with a good

estimate for the population variance.

So what can we use as a point estimator for the population variance? In

other words, how can we use the sample data to find

So what would be a better estimate of the population variance?

Sample vs. Population

flavor duration

frequency

Sample

Population

There are fewer values

in the sample, so there’s

a good chance that

more extreme values will

be excluded.

point estimator for population variance

you are here 4 449

estimating populations and samples

The problem with using the sample variance to estimate that of the population

is that it tends to be slightly too low. The sample variance tends to be slightly

less than the variance of the population, and the degree to which this holds

depends on the number of values in the sample. If the number in the sample

is small, there’s likely to be a bigger difference between the sample and

population variances than if the size of the sample is large.

What we need is a better way of estimating the variance of the population,

some function of the sample data that gives a slightly higher result than the

variance of all the values in the sample.

In other words, we take each item in the sample, subtract the sample mean, and

then square the result. We then add all of the results together, and divide by the

number of items in the sample minus 1. This is just like finding the variance of

the values in the sample, but dividing by n – 1 instead of n.

So what is the estimator?

Rather than take the variance of all the data in the sample to estimate the

population variance, there’s something else we can use instead. If the size of

the sample is n, we can estimate the population variance using

= Σ(x - x)

n - 1

So how is that a

better estimate?

This formula is a closer match to the value of the

population variance.

Dividing a set of numbers by n – 1 gives a higher result than

dividing by n, and this difference is most noticeable when n is fairly

small. This means that the formula is similar to the variance of the

sample data, but gives a slightly higher result.

The population variance tends to be higher than the variance of

the data in the sample. This means that this formula is a slightly

better point estimator for the population variance.

Take each item in the sample, subtract the sample mean,

square the result, then add the lot together.

Divide by the number in the sample minus 1.

Estimator for the

population variance

We need a different point estimator than sample variance

450 Chapter 11

Variance Up Close

Estimating the population variance

If you need to estimate the variance of a population using sample data, use

= Σ(x - x)

n - 1

n - 1, not n, where n is the size of the

sample. This time it’s an estimate..

Instead of calculating the variance of an actual population of n values, you

have to estimate the variance of the population, based on the sample of data

you have. To make you estimate a bit more accurate, you divide by n - 1

instead of n, as this gives a slightly higher result.

The formula for the population variance point estimator is usually written

, so

Sample mean

Point estimator for

the population variance,

based on your sample.

Knowing what formula you should use to find the variance can be confusing.

There’s one formula for population variance σ

, and a slightly different one

for its point estimator σ

. So which formula should you use when?

Population variance

If you want to find the exact variance of a population and you have data for

the whole population, use

= Σ(x - μ)

Population mean

Size of the population

In this situation, you have all the data for your population. You know what

the mean is for your population, and you want to find the variance of all of

these values. This is the calculation that you’ve seen throughout this book

so far.

Population variance

= Σ(x - x)

n - 1

where

= s

This is similar to using x to represent the sample mean.

Point estimator

for the

population

variance

gives the

formula based on

the sample data

variance in depth