Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 461

estimating populations and samples

There are many possible samples we could have taken of size n. Each

possible sample would comprise n gumballs, and the number of red

gumballs in each would follow the same distribution. For each sample, the

number of red gumballs is distributed as B(n, p), and the proportion of

successes is given by X/n.

Each sample contains

n elements, just like

the previous one.

Different samples

X ~ B(n, p)

= X/n

We can form a distribution out of all the sample proportions using all of the

possible samples. This is called the sampling distribution of proportions,

or the distribution of P

X ~ B(n, p)

= X/n

X ~ B(n, p)

= X/n

I get it. The sampling distribution of proportions

is really a probability distribution made up of

the proportions of all possible samples of size

If we know how the proportions are distributed,

we’ll be able to use it to find probabilities for the

proportion of one particular sample.

Using the sampling distribution of proportions,

you can find probabilities for the proportion

of successes in a sample of size n, chosen at

random.

This means that we can use it to find the probability that the

proportion of red gumballs in one particular jumbo box of gumballs

will be at least 40%.

But before we can do that, we need to know what the expectation

and variance is for the distribution.

462 Chapter 11

So what’s the expectation of P

So far we’ve seen how we can form a distribution from the proportions of all

possible samples of size n. Before we can use it to calculate probabilities, we need

to know more about it. In particular, we need to know what the expectation and

variance is of the distribution.

Let’s start with the expectation. Intuitively, we’d expect the proportion of red

gumballs in the sample to match the proportion of red gumballs in the population.

If 25% of the gumball population is red, then you’d expect 25% of the gumballs in

the sample to be red also.

E(P

) = E(X)

= np

= p

Now X is the number of red gumballs in the sample. If we count the number of

red gumballs as the number of successes, then X ~ B(n, p).

You’ve already seen that for a binomial distribution, E(X) = np. This means that

E(P

) = E

(

)

= E(X)

E(X) = np

Intuitively, you’d expect

the proportion of red

gumballs to be the same

both in the sample and the

population.

So what’s the expectation of P

We want to find E(P

), where P

= X/n. In other words, we want to find the expected

value of the sample proportion, where the sample proportion is equal to the number

of red gumballs divided by the total number of gumballs in the sample. This gives us

This result ties in with what we intuitively expect. We can expect the proportion of

successes in the sample to match the proportion of successes in the population.

expectation and variance of P

you are here 4 463

estimating populations and samples

And what’s the variance of P

Before we can find out any probabilities for the sample proportion, we also

need to know what the variance is for P

. We can find the variance in a similar

way to how we find the expectation.

So what’s Var(P

)? Let’s start as we did before by using P

= X/n.

Var(P

) = Var

(

)

= Var(X)

As we’ve said before, X is the number of number of red gumballs in

the sample. If we count the number of red gumballs as the number of

successes, then X ~ B(n, p). This means that Var(X) = npq, as this is the

variance for the binomial distribution. This gives us

Taking the square root of the variance gives us the standard deviation of P

and this tells us how far away from p the sample proportion is likely to be. It’s

sometimes called the standard error of proportion, as it tells you what the

error for the proportion is likely to be in the sample.

Standard error of proportion =

√

The standard error of proportion gets smaller as n gets larger. This means

that the more items there are in your sample, the more reliable your sample

proportion becomes as an estimator for p.

So how can we use the expectation and variance values we found to calculate

probabilities for the proportion? Let’s take a look.

This comes from Var(aX) = a

Var(X).

In this case, a = 1/n.

Var(P

) = Var(X)

= npq

= pq

Var(X) = npq

464 Chapter 11

Find the distribution of P

So far we’ve found the expectation and variance for P

, the sampling

distribution of proportions. We’ve found that if we form a distribution from

all the sample proportions, then

E(P

) = p Var(P

) = pq

We can use this to help us find the probability that the proportion of red

gumballs in a sample of 100 is at least 40%.

But how? Don’t we need to

know what the distribution

of P

is first?

Right, the distribution of P

actually depends on

the size of the samples.

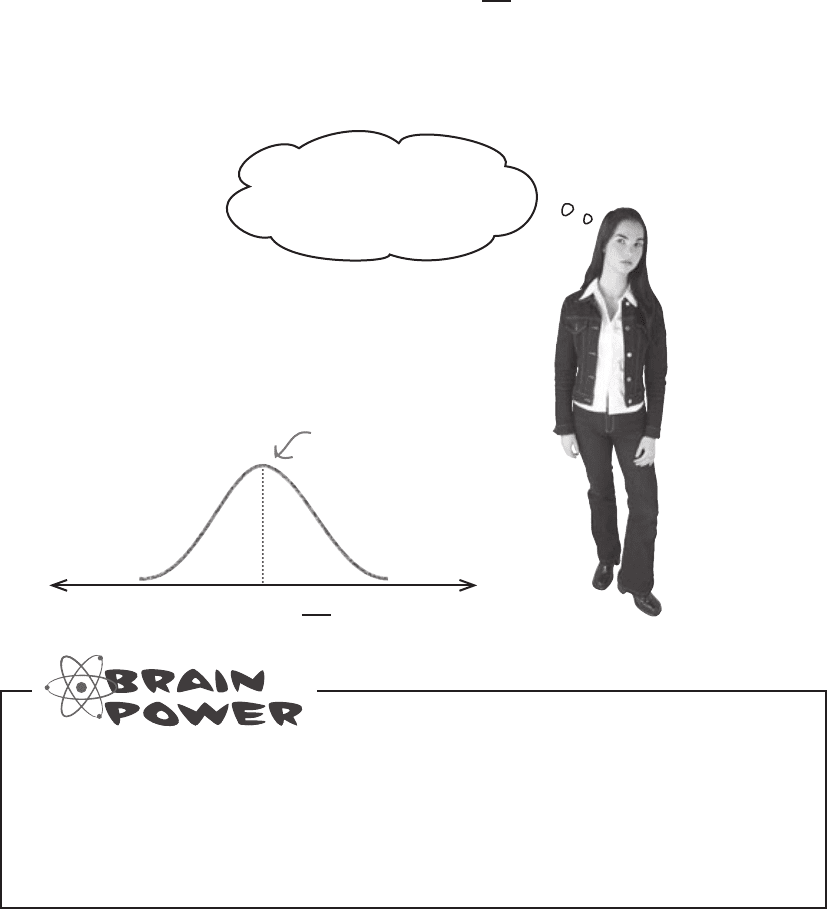
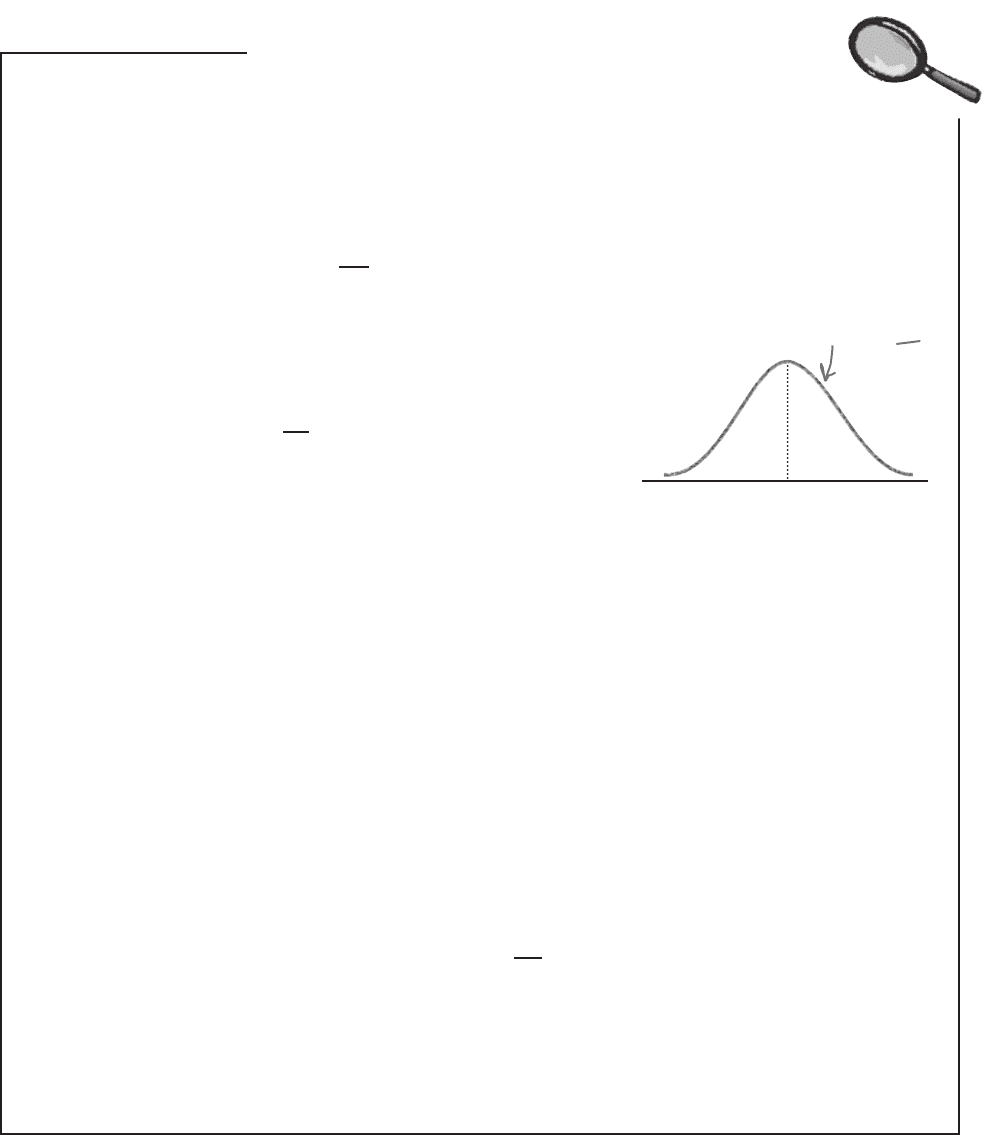
Here’s a sketch of the distribution for P

when n is large.

Take a look at the sketch for the distribution of P

where n is large. How do you

think P

is distributed?

Expectation = p

distribution of P

variance = pq

you are here 4 465

estimating populations and samples

follows a normal distribution

When n is large, the distribution of P

becomes approximately normal.

By large, we mean greater than 30. The larger n gets, the closer the

distribution of P

gets to the normal distribution.

We’ve already found the expectation and variance of P

, so this means

that if n is large,

~ N

(

)

As P

follows a normal distribution for n > 30, this means that we can use

the normal distribution to solve our gumball problem. We can use the

normal distribution to calculate the probability that the proportion of red

gumballs in a jumbo box of gumballs will be at least 40%.

There’s just one thing to remember: the sampling distribution needs a

continuity correction.

In other words, if you use the normal distribution to approximate

probabilities for P

, make sure you apply a continuity correction of

±1/2n. The exact continuity correction depends on the value of n.

—continuity correction required

The number of successes in each of the samples is discrete, and as it’s

used to calculate proportion, you need to apply a continuity correction

when you use the normal distribution to find probabilities.

We’ve seen before that if X represents the number of successes in the

sample, then P

= X/n. The normal continuity correction for X is ±(1/2).

If we substitute this in place of X in the formula P

= X/n, this means

that the continuity correction for P

is given by

Continuity correction = ±(1/2)

= ±1

If n is very

large, the

continuity

correction can

be left out.

As n gets larger, the

continuity correction becomes very

small, and this means that it makes

very little difference to the overall

probability. Some textbooks omit the

continuity correction altogether.

Sometimes

statisticians

disagree about

how large n

needs to be.

If you’re taking a statistics exam,

make sure that you check how

your exam board defines this.

466 Chapter 11

What’s a sampling distribution?

A: A sampling distribution is what you get

if you take lots of different samples from a

single population, all of the same size and

taken in the same way, and then form a

distribution out of some key characteristic of

each sample. This means that the sampling

distribution of proportions is what you get if

you form a sampling distribution out of the

proportions for each of the samples.

Do we actually have to gather all

possible samples?

A: No, we don’t have to physically form all

of the samples. Instead we imagine that we

do, and then come up with expressions for

the expectation and variance.

So a sampling distribution has an

expectation and variance? Why?

A: A sampling distribution is a probability

distribution in the same way as any

other probability distribution, so it has an

expectation and variance.

The expectation of the sampling population

of proportions is like the average value of

a sample proportion; it’s what you expect

the proportion of a sample taken from a

particular population to be.

Why isn’t the variance of P

the

same as the population variance σ

A: The variance for the sampling

distribution of proportions describes how

the sample proportions vary. It doesn’t

describe how the values themselves vary.

The variance has a different value because it

describes a different concept.

So what use does the sampling

distribution of proportions have?

A: It allows you to work out probabilities

for the proportion of a sample taken from a

known population. It gives you an idea of

what you can expect a sample to be like.

What does the standard error of

proportion really mean?

A: The standard error is the square root

of the variance for the sampling distribution.

In effect, it tells you how far away you can

expect the sample proportion to be from the

true value of the population proportion. This

means it tells you what sort of error you can

expect to have.

The sampling distribution of proportions is

what you get if you consider all possible samples

of size n taken from the same population and form

a distribution out of their proportions. We use P

represent the sample proportion random variable.

The expectation and variance of P

are defined as

E(P

) = p

Var(P

) = pq/n

where p is the population proportion.



The standard error of proportion is the standard

deviation of this distribution. It’s given by

√Var(P

)

If n > 30, then P

follows a normal distribution, so

~ N(p, pq/n)

for large n. When working with this, you need to

apply a continuity correction of

± 1



no dumb questions and bullet points

you are here 4 467

estimating populations and samples

25% of the gumball population are red. What’s the probability that in a box of 100 gumballs, at

least 40% will be red? We’ll guide you through the steps.

1. If P

is the proportion of red gumballs in the box, how is P

distributed?

2. What’s the value of P(P

≥ 0.4)?

Hint: Remember to apply a

continuity correction.

468 Chapter 11

25% of the gumball population are red. What’s the probability that in a box of 100 gumballs, at

least 40% will be red? We’ll guide you through the steps.

Let’s use p to represent the probability that a gumball is red. In other words, p = 0.25.

Let’s use P

to represent the proportion of gumballs in the box that are red.

~ N(p, pq/n), where p = 0.25, q = 0.75, and n = 100. As pq/n is equal to 0.25 x 0.75 / 100 = 0.001875,

this gives us

~ N(0.25, 0.001875)

1. If P

is the proportion of red gumballs in the box, how is P

distributed?

2. What’s the value of P(P

≥ 0.4)? Hint: Remember that you need to apply a continuity correction.

P(P

≥ 0.4) = P(P

> 0.4 - 1/(2 x 100))

= P(P

> 0.395)

As P

~ N(0.25, 0.001875), we need to find the standard score of 0.395 so that we can look up the result in

probability tables. This gives us

z = 0.395 - 0.25

√0.001875

= 3.35

P(Z > z) = 1 - P(Z < 3.35)

= 1 - 0.9996

= 0.0004

In other words, the probability that in a box of 100 gumballs, at least 40% will be red, is 0.0004.

A probability of

0.0004? Forget it. I’m

getting popcorn instead.

exercise solution

you are here 4 469

estimating populations and samples

Sampling Distribution of Proportions Up Close

The sampling distribution of proportions is the distribution formed by

taking the proportions of all possible samples of size n. The proportion

of successes in a sample is represented by P

, and it is is distributed as

E(P

) = p

Var(P

) = pq

When n is large, say bigger than 30, the distribution of P

becomes

approximately normal, so

~ N

(

)

Knowing the probability distribution of P

is useful because it means that

given a particular population, we can calculate probabilities for the proportion

of successes in the sample. We can approximate this with the normal

distribution, and the larger the size of the sample, the more accurate the

approximation.

The sampling distribution continuity correction

When you use the normal distribution in this way, it’s important to apply

a continuity correction. This is because the number of successes in the

sample is discrete, and it’s used in the calculation of proportion.

If X represents the number of successes in the sample, then P

= X/n. The

continuity correction for X is ±(1/2), so this means the continuity correction is

given by

Continuity correction = ±1

In other words, if you use the normal distribution to approximate

probabilities for the sampling proportion, make sure you apply a continuity

correction of ±1/2n.

Variance = pq

470 Chapter 11

How many gumballs?

Using the sampling distribution of proportions, you’ve successfully

managed to find the probability of getting a certain proportion of

successes in one particular sample. This means that you can now use

samples to predict what the population will be like, and also use your

knowledge of the population to make predictions about samples.

There’s just one more problem...

The Mighty Gumball CEO has one more problem for you to work on. In

addition to selling jumbo boxes, gumballs are also sold in handy pocket-

sized packets that you can carry with you wherever you go.

According to Mighty Gumball’s statistics for the population, the mean

number of gumballs in each packet is 10, and the variance is 1. The

trouble is they’ve had a complaint. One of their most faithful customers

bought 30 packets of gumballs, and he found that the average number of

gumballs per packet in his sample is only 8.5.

The CEO is concerned that he will lose one of his best customers, and he

wants to offer him some form of compensation. The trouble is, he doesn’t

want to compensate all of his customers. He needs to know what the

probability is of this happening again.

I’m impressed. Really

impressed. Now, there’s

just one more thing that

needs sorting out...

What do you need to know in order to solve this sort of problem?

distribution of sample means